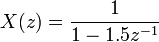La th??orie du contr??le
Contexte des ??coles Wikip??dia
Enfants SOS ont produit une s??lection d'articles de wikipedia pour les ??coles depuis 2005. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .
La th??orie du contr??le est une branche interdisciplinaire de l'ing??nierie et des math??matiques , qui traite avec le comportement de syst??mes dynamiques. La sortie souhait??e d'un syst??me est appel?? r??f??rence. Lorsque une ou plusieurs variables de sortie d'un syst??me doivent suivre une certaine r??f??rence au fil du temps, un contr??leur manipule les entr??es ?? un syst??me pour obtenir l'effet d??sir?? sur la sortie du syst??me.
| Wikibooks a un livre sur le th??me de: Syst??mes de contr??le |
Vue d'ensemble
La th??orie du contr??le est
- la th??orie, qui traite influencer le comportement des syst??mes dynamiques
- sous-champ interdisciplinaire de la science qui trouve son origine dans l'ing??nierie et les math??matiques , et a ??volu?? vers l'utilisation par les sciences sociales, comme la psychologie , la sociologie et criminologie.
Un exemple
Envisager une automobile de r??gulateur de vitesse, qui est un dispositif con??u pour maintenir une vitesse constante du v??hicule; la vitesse de consigne ou de r??f??rence, fournies par le pilote. Le syst??me est dans ce cas le v??hicule. La sortie du syst??me est la vitesse du v??hicule, et la grandeur de commande est un moteur de position du papillon qui influence moteur sortie de couple.
Une fa??on simple de mettre en ??uvre le r??gulateur de vitesse est de verrouiller la position du papillon lorsque le conducteur engage r??gulateur de vitesse. Cependant, sur un terrain vallonn??, le v??hicule ralentit en mont??e et acc??l??rer descente. En fait, ne importe quel param??tre diff??rent de ce qui a ??t?? pris au moment du design se traduira par une erreur proportionnelle ?? la vitesse de sortie, y compris la masse exacte du v??hicule, la r??sistance au vent, et de la pression des pneus. Ce type de commande est appel?? un contr??leur en boucle ouverte parce qu'il n'y a pas de connexion directe entre la sortie du syst??me (le couple moteur) et les conditions r??elles rencontr??es; ce est-??-dire, le syst??me ne fonctionne pas et ne peut pas compenser les forces inattendues.
Dans un syst??me de commande en boucle ferm??e, un capteur surveille la sortie (la vitesse du v??hicule) et alimente les donn??es ?? un ordinateur qui ajuste en permanence l'entr??e de commande (le gaz) que n??cessaire pour que l'??cart de r??gulation ?? un minimum (pour maintenir la souhait??e vitesse). Commentaires sur la fa??on dont le syst??me effectue en fait permet au contr??leur (v??hicule est l'ordinateur de bord) pour compenser dynamiquement pour les perturbations du syst??me, tels que les changements dans la pente de la vitesse au sol ou le vent. Un syst??me de contr??le de r??troaction id??ale annule toutes les erreurs, att??nuer efficacement les effets de toutes les forces qui peuvent ou peuvent ne pas survenir pendant le fonctionnement et produisant une r??ponse dans le syst??me qui correspond parfaitement aux souhaits de l'utilisateur.
Histoire
Bien que les syst??mes de contr??le de diff??rents types remontent ?? l'antiquit??, une analyse plus formelle du champ a commenc?? par une analyse de la dynamique de la r??gulateur centrifuge, men??e par le physicien James Clerk Maxwell en 1868 intitul?? On gouverneurs. Ce d??crit et analys?? le ph??nom??ne de la ??chasse??, dans lequel les retards dans le syst??me peut conduire ?? une surcompensation et le comportement instable. Cela a g??n??r?? une vague d'int??r??t dans le sujet, au cours de laquelle le camarade de classe de Maxwell Edward John Routh g??n??raliser les r??sultats de Maxwell pour la classe g??n??rale des syst??mes lin??aires. Ind??pendamment, Adolf Hurwitz analys?? la stabilit?? du syst??me en utilisant des ??quations diff??rentielles en 1877 . Ce r??sultat est appel?? le Th??or??me de Routh-Hurwitz.
Une application notable de contr??le dynamique ??tait dans le domaine des vols habit??s. Les fr??res Wright ont fait leurs premiers vols d'essai r??ussis sur 17 d??cembre 1903 et se distinguent par leur capacit?? ?? contr??ler leurs vols pour de longues p??riodes (plus que la capacit?? de produire de la portance d'une surface portante, qui ??tait connu). Contr??le de l'avion ??tait n??cessaire pour la s??curit?? du vol.
Par la Seconde Guerre mondiale , la th??orie du contr??le ??tait une partie importante de syst??mes de commande de tir, syst??mes de guidage et de l'??lectronique . La course de l'espace d??pend aussi sur le contr??le de l'engin spatial pr??cis. Cependant, la th??orie du contr??le a ??galement vu une utilisation croissante dans des domaines comme l'??conomie .
Les gens dans les syst??mes et le contr??le
De nombreuses personnalit??s actives et historiques faites contribution significative ?? contr??ler la th??orie, par exemple:
- Alexander Lyapunov (1857-1918) dans les ann??es 1890 marque le d??but de th??orie de la stabilit??.
- Harold S. Black (1898-1983), a invent?? le amplificateur de r??troaction n??gative dans les ann??es 1930.
- Harry Nyquist (1889-1976), a d??velopp?? le Crit??re de stabilit?? de Nyquist pour les syst??mes de r??troaction dans les ann??es 1930.
- Richard Bellman (1920-1984), d??velopp?? programmation dynamique depuis les ann??es 1940.
- Norbert Wiener (1894-1964) a invent?? le terme Cybern??tique dans les ann??es 1940.
- John R. Ragazzini (1912-1988) introduit commande num??rique et de la z transformer dans les ann??es 1950.
Th??orie du contr??le classique: le contr??leur en boucle ferm??e
Pour ??viter les probl??mes de la commande en boucle ouverte, contr??ler introduit la th??orie r??troaction. Une boucle ferm??e contr??leur utilise la r??troaction au contr??le Unis ou des sorties d'un syst??me dynamique. Son nom vient de la voie de l'information dans le syst??me: entr??es de processus (par exemple, la tension appliqu??e ?? un moteur ??lectrique) avoir un effet sur les sorties de processus (par exemple la vitesse ou le couple du moteur), qui est mesur??e avec capteurs et trait??es par le contr??leur; le r??sultat (le signal de commande) est utilis?? comme entr??e pour le processus, la fermeture de la boucle.
Contr??leurs en boucle ferm??e pr??sentent les avantages suivants par rapport aux contr??leurs ?? boucle ouverte:
- rejet de perturbation (tels que le frottement non mesur??e dans un moteur)
- performance garantie m??me avec les incertitudes des mod??les, lorsque la structure du mod??le ne correspond pas parfaitement le processus r??el et les param??tres du mod??le ne sont pas exactes
- processus instables peuvent ??tre stabilis??es
- une sensibilit?? r??duite ?? des variations de param??tres
- performances de suivi am??lior?? de r??f??rence
Dans certains syst??mes, en boucle ferm??e et en boucle ouverte de contr??le sont utilis??s simultan??ment. Dans ces syst??mes, la commande en boucle ouverte est appel??e anticipation et sert ?? am??liorer encore les performances de suivi de r??f??rence.
Une architecture de contr??leur en boucle ferm??e commune est le R??gulateur PID.
La sortie du syst??me y (t) est renvoy??e ?? la valeur r de r??f??rence (t), par une mesure de capteur. Le dispositif de commande C prend alors l'e d'erreur (diff??rence) entre la r??f??rence et la sortie pour modifier les entr??es u au syst??me sous la commande P. Ceci est repr??sent?? sur la figure. Ce type de contr??leur est un contr??leur de dispositif de commande ou de la r??troaction en boucle ferm??e.
Cela se appelle une seule entr??e-sortie unique (SISO) syst??me de contr??le; MIMO (Multi-dire entr??e-sorties multiples) syst??mes, avec plus d'une entr??e / sortie, sont communs. Dans de tels cas les variables sont repr??sent??s par vecteurs au lieu de simples valeurs scalaires. Pour certains syst??mes ?? param??tres r??partis les vecteurs peuvent ??tre infinite- dimensions (typiquement fonctions).

Si nous supposons que le contr??leur C et l'usine sont P lin??aire et invariant dans le temps (ex: ??l??ments de leur fonction de transfert C (s) et P (s) ne d??pend pas de temps), les syst??mes ci-dessus peuvent ??tre analys??s en utilisant le Transform??e de Laplace sur les variables. On obtient les relations suivantes:
R??solution Y (s) en termes de R (s) donne:
Le terme 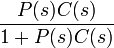 que l'on appelle la fonction de transfert du syst??me. Le num??rateur est le gain vers l'avant ?? partir de R ?? Y, et le d??nominateur est un plus le gain de boucle de la boucle de r??troaction. Si
que l'on appelle la fonction de transfert du syst??me. Le num??rateur est le gain vers l'avant ?? partir de R ?? Y, et le d??nominateur est un plus le gain de boucle de la boucle de r??troaction. Si 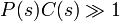 , Ce est ?? dire qu'il a un grand norme avec chaque valeur de s, alors Y (s) est approximativement ??gale ?? R (s). Cela implique de mettre tout simplement la r??f??rence contr??le la sortie.
, Ce est ?? dire qu'il a un grand norme avec chaque valeur de s, alors Y (s) est approximativement ??gale ?? R (s). Cela implique de mettre tout simplement la r??f??rence contr??le la sortie.
Sujet de la th??orie du contr??le
Stabilit??
Stabilit?? (en th??orie du contr??le) signifie souvent que pour toute entr??e born??e sur un montant de temps, la sortie sera ??galement limit??e. Ceci est connu comme La stabilit?? BIBO (voir aussi Lyapunov stabilit??). Si un syst??me est BIBO stable alors la sortie ne peut pas "sauter" (ce est ?? dire, devenir infinie) si l'entr??e reste finie. Math??matiquement, cela signifie que pour un syst??me lin??aire causal soit stable tout le p??les de son fonction de transfert doit satisfaire ?? certains crit??res en fonction de si une analyse continue ou discr??te de temps est utilis??e:
- En temps continu, le Transform??e de Laplace est utilis??e pour obtenir la fonction de transfert. Un syst??me est stable si les p??les de cette fonction de transfert se trouvent strictement dans la moiti?? gauche ferm??e du plan complexe . ce est ?? dire la partie r??elle de l'ensemble des p??les est inf??rieur ?? z??ro).
OU
- En temps discret du Z transform??e est utilis??e. Un syst??me est stable si les p??les de cette fonction de transfert se trouvent ?? l'int??rieur du strictyly cercle unit??. ce est ?? dire l'amplitude des p??les est inf??rieur ?? un).
Lorsque les conditions ci-dessus sont appropri??es satisfait un syst??me est dit ??tre asymptotiquement stable: les variables d'un syst??me de commande diminuent toujours asymptotiquement stable ?? partir de sa valeur initiale et ne montrent pas oscillations permanentes. Oscillations permanentes se produire lorsque un p??le a une partie r??elle exactement ??gale ?? z??ro (dans le cas de temps continu) ou un module ??gale ?? une (dans le cas de temps discret). Si une r??ponse du syst??me stable tout simplement ne se d??sint??gre, ni se d??veloppe au fil du temps, et n'a pas d'oscillations, il est marginalement stable: dans ce cas, la fonction de transfert du syst??me a des p??les non r??p??t??es ?? l'origine de plan complexe (ce est ?? dire leur composante r??elle et complexe est nulle dans le cas de temps continu). Oscillations sont pr??sents lorsque p??les avec partie r??elle ??gale ?? z??ro ont une partie imaginaire est pas ??gal ?? z??ro.
Les diff??rences entre les deux cas ne sont pas une contradiction. La transformation de Laplace est en coordonn??es cart??siennes et de la Z-transform est en coordonn??es circulaires , et il peut ??tre d??montr?? que
- la partie n??gative r??el dans le domaine de Laplace peut mapper sur l'int??rieur du cercle unit??
- la partie positive-r??el dans le domaine de Laplace peut mapper sur l'ext??rieur du cercle unit??
Si un syst??me en question a une r??ponse impulsionnelle
puis le Z-transform (voir cet exemple), est donn??e par
qui a un pole  (Z??ro partie imaginaire). Ce syst??me est BIBO (asymptotiquement) stable puisque le p??le est ?? l'int??rieur du cercle unit??.
(Z??ro partie imaginaire). Ce syst??me est BIBO (asymptotiquement) stable puisque le p??le est ?? l'int??rieur du cercle unit??.
Cependant, si la r??ponse impulsionnelle est
alors le Z-transform est
qui a un p??le ?? 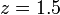 et ne est pas BIBO stable puisque le p??le a un module strictement sup??rieur ?? un.
et ne est pas BIBO stable puisque le p??le a un module strictement sup??rieur ?? un.
De nombreux outils existent pour l'analyse des p??les d'un syst??me. Il se agit notamment des syst??mes graphiques comme le lieu des racines, parcelles de Bode ou Parcelles de Nyquist.
Contr??labilit?? et observabilit??
Contr??labilit?? et observabilit?? sont principales questions ?? l'analyse d'un syst??me avant de d??cider de la meilleure strat??gie de lutte ?? appliquer, ou se il est m??me possible de contr??ler ou ?? stabiliser le syst??me. Contr??labilit?? est li??e ?? la possibilit?? de forcer le syst??me dans un ??tat particulier en utilisant un signal de contr??le appropri??. Si un Etat ne est pas contr??lable, aucun signal ne sera jamais en mesure de contr??ler l'??tat. Si un Etat ne est pas contr??lable, mais sa dynamique sont stables, alors l'??tat o?? il est appel?? stabilisable. Observabilit?? place est li??e ?? la possibilit?? d'une "observation", par des mesures de sortie, l'??tat d'un syst??me. Si un Etat ne est pas observable, le contr??leur ne sera jamais en mesure de d??terminer le comportement d'un Etat non observables et donc ne peut pas l'utiliser pour stabiliser le syst??me. Toutefois, m??me ?? l'??tat de stabilisabilit?? ci-dessus, si un ??tat ne peut pas ??tre observ?? il pourrait encore ??tre d??tectable.
D'un point de vue g??om??trique, en regardant les ??tats de chaque variable du syst??me ?? ??tre contr??l??, tous les ??mauvais?? ??tat de ces variables doit ??tre contr??lable et observable pour assurer un bon comportement dans le syst??me en boucle ferm??e. Ce est, si l'une des valeurs propres du syst??me ne est pas ?? la fois contr??lable et observable, cette partie de la dynamique restera intacte dans le syst??me en boucle ferm??e. Si une telle valeur propre ne est pas stable, la dynamique de cette valeur propre sera pr??sent dans le syst??me en boucle ferm??e qui sera donc instable. P??les non observables ne sont pas pr??sents dans la fonction de transfert r??alisation d'une repr??sentation d'??tat, ce est pourquoi parfois ce dernier est pr??f??r?? dans l'analyse des syst??mes dynamiques.
Les solutions aux probl??mes de syst??me incontr??lable ou inobservable comprennent l'ajout de capteurs et actionneurs.
Sp??cifications de contr??le
Plusieurs strat??gies de contr??le diff??rents ont ??t?? mis au point dans les derni??res ann??es. Celles-ci varient de celles extr??mement g??n??rales ( R??gulateur PID), ?? d'autres consacr?? ?? m??mes cat??gories particuli??res de syst??mes (en particulier robotique ou avions r??gulateur de vitesse).
Un probl??me de contr??le peut avoir plusieurs sp??cifications. Stabilit??, bien s??r, est toujours pr??sent: le contr??leur doit se assurer que le syst??me en boucle ferm??e est stable, ind??pendamment de la stabilit?? en boucle ouverte. Un mauvais choix de contr??leur peut m??me aggraver la stabilit?? du syst??me en boucle ouverte, qui doit normalement ??tre ??vit??e. Parfois, il serait souhaitable d'obtenir une dynamique particuli??re dans la boucle ferm??e: ce est ?? dire que les p??les ont ![Re [\ lambda] <- \ overline {\ lambda}](../../images/190/19048.png) O??
O?? 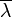 est une valeur fixe strictement sup??rieure ?? z??ro, au lieu de simplement demander que
est une valeur fixe strictement sup??rieure ?? z??ro, au lieu de simplement demander que ![Re [\ lambda] <0](../../images/190/19050.png) .
.
Une autre sp??cification typique est le rejet d'une perturbation de l'??tape; comprenant un int??grateur de la cha??ne en boucle ouverte (ce est ?? dire juste avant le syst??me sous contr??le) r??alise facilement cela. D'autres classes de perturbations besoin de diff??rents types de sous-syst??mes pour ??tre inclus.
Autres caract??ristiques ??classiques?? de la th??orie de contr??le consid??rent le temps de r??ponse du syst??me en boucle ferm??e: il se agit notamment de la temps de mont??e (le temps requis par le syst??me de contr??le pour atteindre la valeur d??sir??e apr??s une perturbation), le pic d??passement (la plus haute valeur atteinte par la r??ponse avant d'atteindre la valeur souhait??e) et autres ( temps de stabilisation, quart de pourriture). les sp??cifications de domaine de fr??quence sont g??n??ralement li??s ?? robustesse (voir apr??s).
??valuations de performance modernes utilisent une variation d'erreur de suivi int??gr?? (IAE, ISA, CQI).
l'identification du mod??le et la robustesse
Un syst??me de contr??le doit toujours avoir une certaine propri??t?? de robustesse. Un correcteur robuste est tel que ses propri??t??s ne changent pas beaucoup si elle est appliqu??e ?? un syst??me l??g??rement diff??rent de celui math??matique utilis?? pour sa synth??se. Cette sp??cification est important: aucun syst??me physique r??el se comporte vraiment comme la s??rie d'??quations diff??rentielles utilis??es pour repr??senter math??matiquement. Typiquement, un mod??le math??matique simple est choisi pour simplifier les calculs, sinon les vrais dynamique du syst??me peuvent ??tre si compliqu?? que d'un mod??le complet est impossible.
Identification du syst??me
Le processus de d??termination des ??quations qui r??gissent la dynamique du mod??le est appel?? identification de syst??me. Cela peut se faire hors ligne: par exemple, l'ex??cution d'une s??rie de mesures ?? partir de laquelle calculer un mod??le math??matique approch??e, g??n??ralement son fonction de transfert ou une matrice. Cette identification de la sortie, cependant, ne peut pas tenir compte de la dynamique non observables. Parfois, le mod??le est construit directement ?? partir des ??quations physiques connues: par exemple, dans le cas d'un syst??me masse-ressort-amortisseur nous savons que  . M??me en supposant que le mod??le ??complet?? est utilis?? dans la conception du contr??leur, tous les param??tres inclus dans ces ??quations (appel??s ??param??tres nominaux") ne sont jamais connue avec une pr??cision absolue; le syst??me de contr??le devra comporter correctement m??me lorsque vous ??tes connect?? ?? un syst??me physique avec les vraies valeurs de param??tres loin de nominal.
. M??me en supposant que le mod??le ??complet?? est utilis?? dans la conception du contr??leur, tous les param??tres inclus dans ces ??quations (appel??s ??param??tres nominaux") ne sont jamais connue avec une pr??cision absolue; le syst??me de contr??le devra comporter correctement m??me lorsque vous ??tes connect?? ?? un syst??me physique avec les vraies valeurs de param??tres loin de nominal.
Certaines techniques de contr??le avanc??es incluent un processus d'identification "on-line" (voir plus loin). Les param??tres du mod??le sont calcul??s ("identifi??"), tandis que le dispositif de commande lui-m??me est en cours d'ex??cution: de cette mani??re, si une variation drastique des param??tres se ensuit (par exemple, si le bras de robot lib??re un poids), le contr??leur se ajustera en cons??quence afin d'assurer la bonne ex??cution.
Analyse
L'analyse de la robustesse d'un syst??me de contr??le de SISO peut ??tre effectu??e dans le domaine des fr??quences, en tenant compte de la fonction de transfert du syst??me et l'utilisation Nyquist et diagrammes de Bode. Les sujets trait??s comprennent gain et la phase de marge et la marge d'amplitude. Pour MIMO et, en g??n??ral des syst??mes de contr??le, plus complexes, il faut examiner les r??sultats th??oriques ??labor??s pour chaque technique de contr??le (voir la section suivante): par exemple, si des qualit??s particuli??res de robustesse sont n??cessaires, l'ing??nieur doit passer son attention sur une technique de contr??le de les inclure dans ses propri??t??s.
Contraintes
Un probl??me de robustesse particuli??re est l'exigence d'un syst??me de contr??le pour effectuer correctement en pr??sence de contraintes sur les intrants et de l'Etat. Dans le monde physique chaque signal est limit??e. Il peut arriver qu'un contr??leur envoie des signaux de commande qui ne peuvent pas ??tre suivies par le syst??me physique: par exemple, en essayant de faire tourner une valve ?? une vitesse excessive. Cela peut produire un comportement ind??sirable du syst??me en boucle ferm??e, ou m??me briser actionneurs ou d'autres sous-syst??mes. Techniques de contr??le sp??cifiques sont disponibles pour r??soudre le probl??me: mod??liser commande pr??dictive (voir plus loin), et anti-vent en place des syst??mes. Ce dernier est constitu?? d'un bloc de commande suppl??mentaire qui se assure que le signal de commande ne d??passe un seuil donn??.
Strat??gies de contr??le principales
Chaque syst??me de contr??le doit garantir abord la stabilit?? du comportement en boucle ferm??e. Pour syst??mes lin??aires, ceci peut ??tre obtenu en pla??ant directement les p??les. Les syst??mes de contr??le non lin??aires utilisent des th??ories particuli??res (normalement bas??s sur La th??orie de Aleksandr Lyapunov) pour assurer la stabilit??, sans ??gard ?? la dynamique interne du syst??me. La possibilit?? de remplir des sp??cifications diff??rentes varie du mod??le consid??r?? et de la strat??gie de contr??le choisi. Voici une liste sommaire des principales techniques de contr??le se affiche:
Contr??le classique
Le R??gulateur PID est probablement la conception la plus utilis??e asservissement la, ??tant la plus simple. "PID" signifie proportionnelle, int??grale et d??riv??e, en se r??f??rant aux trois conditions op??rantes sur le signal d'erreur pour produire un signal de commande. Si u (t) est le signal de commande envoy?? au syst??me, y (t) est la sortie mesur??e et r (t) est la sortie d??sir??e, et l'erreur de suivi 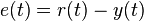 , Un r??gulateur PID a la forme g??n??rale
, Un r??gulateur PID a la forme g??n??rale
Les dynamiques d??sir??es en boucle ferm??e est obtenu en ajustant les trois param??tres 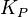 ,
, 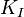 et
et 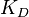 , Souvent de mani??re it??rative par "tuning" et sans connaissances sp??cifiques d'un mod??le de plante. La stabilit?? peut souvent ??tre assur??e en utilisant uniquement le terme proportionnel. Le terme int??gral permet le rejet d'une perturbation de l'??tape (souvent une sp??cification en frappant contr??le de processus). Le terme d??riv?? est utilis?? pour fournir d'amortissement ou de fa??onnage de la r??ponse. Contr??leurs PID sont la classe la plus bien ??tabli des syst??mes de contr??le: cependant, ils ne peuvent pas ??tre utilis??s dans plusieurs cas plus compliqu??s, surtout si les syst??mes MIMO sont consid??r??s.
, Souvent de mani??re it??rative par "tuning" et sans connaissances sp??cifiques d'un mod??le de plante. La stabilit?? peut souvent ??tre assur??e en utilisant uniquement le terme proportionnel. Le terme int??gral permet le rejet d'une perturbation de l'??tape (souvent une sp??cification en frappant contr??le de processus). Le terme d??riv?? est utilis?? pour fournir d'amortissement ou de fa??onnage de la r??ponse. Contr??leurs PID sont la classe la plus bien ??tabli des syst??mes de contr??le: cependant, ils ne peuvent pas ??tre utilis??s dans plusieurs cas plus compliqu??s, surtout si les syst??mes MIMO sont consid??r??s.
Contr??le lin??aire
Pour les syst??mes MIMO, placement de p??les peut ??tre r??alis?? en utilisant un math??matiquement Etat repr??sentation spatiale du syst??me en boucle ouverte et le calcul d'une matrice de contre-r??action attribution p??les dans les positions souhait??es. Dans les syst??mes complexes cela peut n??cessiter des capacit??s de calcul assist?? par ordinateur, et ne peut pas toujours assurer la robustesse. En outre, tous les Etats du syst??me ne sont pas en observateurs mesur??es et si g??n??rale doivent ??tre inclus et int??gr??s dans la conception de placement de p??les.
Commande non lin??aire
Processus dans les industries comme la robotique et de la industrie a??rospatiale ont g??n??ralement forte dynamique non-lin??aire. Dans la th??orie de contr??le, il est parfois possible de lin??ariser ces classes de syst??mes et appliquer des techniques lin??aires: mais dans de nombreux cas, il peut ??tre n??cessaire de concevoir des th??ories ?? gratter permettant le contr??le des syst??mes non lin??aires. Il se agit, par exemple, r??troaction lin??arisation, backstepping, commande coulissante de mode, le contr??le de lin??arisation trajectoire normalement prendre avantage des r??sultats repose sur Th??orie. Lyapunov de la g??om??trie diff??rentielle a ??t?? largement utilis?? comme un outil pour la g??n??ralisation des concepts de contr??le lin??aires bien connues pour le cas non-lin??aire, ainsi que de montrer les subtilit??s qui font ce un probl??me plus difficile.
Contr??le optimal
Commande optimale est une technique de contr??le particulier dans lequel le signal de commande permet d'optimiser un certain ??indice de co??t??: par exemple, dans le cas d'un satellite, les axes des jets n??cessaires pour l'amener ?? la trajectoire d??sir??e qui consomme le moins de combustible. Deux m??thodes de conception optimale de contr??le ont ??t?? largement utilis??s dans des applications industrielles, comme il a ??t?? montr?? qu'elles peuvent garantir la stabilit?? en boucle ferm??e. Ceux-ci sont Mod??le Predictive Control (MPC) et Commande LQG (LQG). Le premier peut prendre plus explicitement en compte les contraintes sur les signaux dans le syst??me, qui est un ??l??ment important dans de nombreux processus industriels. Cependant, la structure "de la commande optimale" dans les PPM ne est qu'un moyen pour atteindre un tel r??sultat, car il ne optimise pas un v??ritable indice de performance du syst??me de contr??le en boucle ferm??e. Ensemble avec les contr??leurs PID, syst??mes MPC sont la technique de contr??le le plus largement utilis?? dans contr??le de processus.
Contr??le adaptatif
Contr??le adaptatif utilise l'identification en ligne des param??tres du proc??d??, ou la modification des gains de contr??leur, de fa??on ?? obtenir des propri??t??s de robustesse fortes. Adaptive contr??les ont ??t?? appliqu??es pour la premi??re fois dans la industrie a??rospatiale dans le Ann??es 1950, et ont trouv?? un succ??s particulier dans ce domaine.
Commande intelligente
L'utilisation de contr??le intelligent diverses approches comme l'informatique AI r??seaux de neurones, Probabilit?? bay??sienne, logique floue, l'apprentissage machine, calcul ??volutif et algorithmes g??n??tiques pour contr??ler un syst??me dynamique
Contr??le hi??rarchique
Un syst??me de contr??le hi??rarchique est une forme de Syst??me de contr??le dans lequel un ensemble de dispositifs et de logiciels d'administration est dispos?? dans un hi??rarchique arbre. Lorsque les maillons de l'arbre sont mis en oeuvre par un r??seau informatique, alors que le syst??me de contr??le hi??rarchique est aussi une forme de Syst??me de contr??le en r??seau.
Litt??rature
- Christopher Kilian (2005). Technologie de contr??le moderne. Thompson apprentissage Delmar. ISBN 1-4018-5806-6.
- Vannevar Bush (1929). Analyse circuit op??rationnel. John Wiley and Sons, Inc ..
- Robert F. Stengel (1994). Contr??le optimal et estimation. Dover Publications. ISBN 0-486-68200-5, ISBN-13: 978-0-486-68200-6.
- Franklin et al. (2002). Commentaires contr??le de syst??mes dynamiques (4 ed.). New Jersey: Prentice Hall. ISBN 0-13-032393-4.
- Joseph L. Hellerstein, Dawn M. Tilbury, et Sujay Parekh (2004). Commentaires de contr??le des syst??mes informatiques. John Wiley and Sons. ISBN 0-47-126637-X, ISBN-13: 978-0-471-26637-2.
- Syst??me dynamique et Anthony J. Pritchard (2005) Syst??mes math??matiques Th??orie I -. Mod??lisation, Analyse spatiale ??tat, de stabilit?? et de robustesse. Springer. ISBN 0-978-3-540-44125-0.
- Sontag, Eduardo (1998) la th??orie du contr??le math??matique:. Syst??mes de dimension finie d??terministes. Deuxi??me ??dition. Springer. ISBN 0-387-984895.

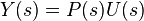

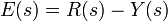
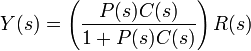
![\ x [n] = 0,5 ^ n u [n]](../../images/190/19042.png)
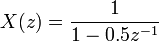
![\ x [n] = 1,5 ^ n u [n]](../../images/190/19045.png)