
La th??orie des jeux
?? propos de ce ??coles s??lection Wikipedia
SOS Enfants, un organisme de bienfaisance de l'??ducation , a organis?? cette s??lection. Une bonne fa??on d'aider d'autres enfants est de parrainer un enfant
| ??conomie |
|---|
 ??conomies par pays |
| Classifications g??n??rales |
|
| M??thodes techniques |
|
| Les champs et sous-champs |
|
| Listes |
|
|
| La th??orie des jeux est inclus dans le JEL codes de classification: JEL: C7 |
La th??orie des jeux est une ??tude de strat??gique la prise de d??cision. Plus formellement, ce est ??l'??tude des des mod??les math??matiques de conflit et de coop??ration entre les d??cideurs rationnels intelligents. "Une alternative terme sugg??r??" comme un nom plus descriptif pour la discipline "est interactive th??orie de la d??cision. La th??orie des jeux est principalement utilis?? dans l'??conomie, la science politique et la psychologie, ainsi que la logique et de la biologie. Le premier sujet abord?? jeux ?? somme nulle, les pertes nettes des gains de telle sorte qu'une personne exactement ??gales de l'autre participant (s). Aujourd'hui, cependant, la th??orie des jeux se applique ?? un large ??ventail de rapports de classe, et a d??velopp?? dans un terme parapluie pour le c??t?? logique de la science, d'inclure les deux-humains non humains et, comme les ordinateurs. Usages classiques comprennent un sens de l'??quilibre dans de nombreux jeux, o?? chaque personne a trouv?? ou d??velopp??s une tactique qui ne peuvent pas mieux avec succ??s ses r??sultats, compte tenu de l'autre approche.
La th??orie des jeux moderne a commenc?? avec l'id??e sur l'existence d'??quilibres en strat??gies mixtes en deux personnes jeux ?? somme nulle et sa preuve par John von Neumann . Preuve de l'origine de Von Neumann utilis??e Point fixe le th??or??me de Brouwer sur applications continues en ensembles convexes compacts, qui est devenue une m??thode standard dans la th??orie des jeux et de l'??conomie math??matique. Son document a ??t?? suivi par son livre 1944 Th??orie des Jeux et le comportement ??conomique, avec Oskar Morgenstern, qui consid??rait les jeux coop??ratifs de plusieurs joueurs. La deuxi??me ??dition de ce livre a fourni une th??orie axiomatique de l'utilit?? esp??r??e, qui a permis aux statisticiens et les ??conomistes math??matiques pour traiter la prise de d??cision en situation d'incertitude.
Cette th??orie a ??t?? largement d??velopp??e dans les ann??es 1950 par de nombreux sp??cialistes. La th??orie des jeux a plus tard ??t?? explicitement appliqu?? ?? la biologie dans les ann??es 1970, bien que des d??veloppements similaires remontent au moins aussi loin que les ann??es 1930. La th??orie des jeux a ??t?? largement reconnu comme un outil important dans de nombreux domaines. Huit jeu th??oriciens ont remport?? le Prix comm??moratif Nobel en sciences ??conomiques, et John Maynard Smith a re??u le Prix Crafoord pour son application de la th??orie des jeux ?? la biologie.
Repr??sentation de jeux
Les jeux ??tudi??s dans la th??orie des jeux sont des objets math??matiques bien d??finis. Un jeu se compose d'un ensemble de joueurs, un ensemble de mouvements (ou strat??gies) disponibles pour les joueurs, et une sp??cification des gains pour chaque combinaison de strat??gies. La plupart des jeux coop??ratifs sont pr??sent??s sous la forme de fonction caract??ristique, tandis que l'??tendue et les formes normales sont utilis??es pour d??finir des jeux non coop??ratifs.
Forme extensive

La forme extensive peut ??tre utilis?? pour officialiser jeux avec un s??quencement de temps de mouvements. Jeux ici sont jou??s sur arbres (comme sur la photo ?? gauche). Ici, chaque sommet (ou n??ud) repr??sente un point de choix pour un joueur. Le joueur est sp??cifi?? par un num??ro indiqu?? par le sommet. Les lignes sur le sommet repr??sentent une action possible pour ce joueur. Les gains sont indiqu??es au bas de l'arbre. La forme extensive peut ??tre consid??r?? comme un multi-joueurs g??n??ralisation d'un arbre de d??cision. (Fudenberg & Tirole 1991, p. 67)
Dans le jeu illustr?? ?? la gauche, il ya deux joueurs. Joueur 1 se d??place d'abord et choisit F ou U. Joueur 2 voit le coup de l 'Joueur 1 puis choisit A ou R. Supposons que le joueur 1 choisit U et alors le joueur 2 choisit A, alors le joueur 1 obtient 8 et Joueur 2 obtient deux.
La forme extensive peut ??galement capturer des jeux simultan??e-d??placer et les jeux ?? information imparfaite. Pour le repr??senter, soit une ligne pointill??e relie diff??rents sommets pour les repr??senter comme faisant partie de la m??me information set (ce est ?? dire, les joueurs ne savent pas ?? quel point ils sont), ou une ligne ferm??e est dessin?? autour d'eux. (Voir l'exemple dans la section de l'information imparfaite .)
Forme normale
| Joueur 2 choisit Gauche | Joueur 2 choisit droit | |
| Joueur 1 choisit Up | 4, 3 | -1, -1 |
| Joueur 1 choisit de Down | 0, 0 | 3, 4 |
| Forme ou gain normal matrice d'un deux-joueur, jeu ?? 2 strat??gie | ||
Le (forme ou strat??gique) normale jeu est g??n??ralement repr??sent?? par une matrice qui montre les joueurs, les strat??gies, et de pay-offs (voir l'exemple ?? la droite). Plus g??n??ralement, il peut ??tre repr??sent?? par une fonction qui associe un gain pour chaque joueur avec toutes les combinaisons possibles d'actions. Dans l'exemple d'accompagnement, il ya deux joueurs; on choisit la ligne et l'autre choisit la colonne. Chaque joueur dispose de deux strat??gies, qui sont sp??cifi??es par le nombre de lignes et le nombre de colonnes. Les gains sont fournis ?? l'int??rieur. Le premier nombre est la r??compense re??ue par le joueur de premi??re ligne (du joueur 1 dans notre exemple); le second est la r??compense pour le joueur de la colonne (du joueur 2 dans notre exemple). Supposons que le joueur 1 joue le haut et que le joueur 2 joue gauche. Ensuite le joueur 1 obtient un paiement de 4, et le joueur 2 obtient trois.
Quand un jeu est pr??sent?? sous forme normale, il est pr??sum?? que chaque joueur agit simultan??ment ou, au moins, sans conna??tre les actions de l'autre. Si les joueurs ont des informations sur les choix des autres joueurs, le jeu est g??n??ralement pr??sent??e sous forme extensive.
Chaque jeu vaste-forme a une normale-forme ??quivalente jeu, cependant la transformation sous forme normale peut entra??ner une explosion combinatoire de la taille de la repr??sentation, ce qui rend impossible de calcul. (Leyton-Brown & Shoham 2008, p. 35)
Formulaire de fonction caract??ristique
Dans les jeux qui poss??dent utilitaire amovible r??compenses s??par??es ne sont pas donn??s; plut??t, la fonction caract??ristique d??cide le gain de chaque unit??. L'id??e est que l'unit?? qui est ??vide??, pour ainsi dire, ne re??oit pas de r??compense ?? tous.
L'origine de cette forme se trouve dans John von Neumann et le livre d'Oskar Morgenstern; quand on regarde ces cas, ils devin?? que quand un syndicat 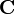 appara??t, il travaille contre la fraction
appara??t, il travaille contre la fraction 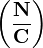 comme si deux personnes jouaient ?? un jeu normal. La r??compense ??quilibr?? de C est une fonction de base. Bien qu'il existe des exemples diff??rents qui aident ?? d??terminer les montants de coalition de jeux normaux, semble pas tout ce qui dans leur forme de fonction peut ??tre d??riv?? de tel.
comme si deux personnes jouaient ?? un jeu normal. La r??compense ??quilibr?? de C est une fonction de base. Bien qu'il existe des exemples diff??rents qui aident ?? d??terminer les montants de coalition de jeux normaux, semble pas tout ce qui dans leur forme de fonction peut ??tre d??riv?? de tel.
Formellement, une fonction caract??ristique est consid??r??e comme: (N, v), o?? N repr??sente le groupe de personnes et  est un utilitaire normal.
est un utilitaire normal.
Ces fonctions caract??ristiques ont ??largi pour d??crire les jeux o?? il ne existe aucun utilitaire amovible.
Partition forme de fonction
Le formulaire de fonction caract??ristique ignore la possible externalit??s de la formation de la coalition. Dans la fonction de partition former le gain d'une coalition d??pend non seulement de ses membres, mais aussi sur la fa??on dont le reste des joueurs sont partag?? (Thrall et Lucas 1963).
G??n??ral et usages appliqu??s
Comme une m??thode de math??matiques appliqu??es , la th??orie des jeux a ??t?? utilis??e pour ??tudier un large ??ventail de comportements humains et animaux. Il a ??t?? initialement d??velopp?? en ??conomie pour comprendre une grande collection de comportements ??conomiques, y compris les comportements des entreprises, les march??s et les consommateurs. L'utilisation de la th??orie des jeux dans les sciences sociales a augment??, et la th??orie des jeux a ??t?? appliqu??e ?? des comportements politiques, sociologiques et psychologiques.
Analyse la th??orie des jeux a d'abord ??t?? utilis??e pour ??tudier le comportement des animaux Ronald Fisher dans les ann??es 1930 (bien que m??me Charles Darwin fait quelques d??clarations de la th??orie des jeux informels). Ce travail est ant??rieure ?? la d??nomination ??th??orie des jeux??, mais elle partage de nombreuses caract??ristiques importantes avec ce domaine. Les d??veloppements dans l'??conomie ont ensuite ??t?? appliqu??es ?? la biologie en grande partie par John Maynard Smith dans son livre Evolution et la th??orie des jeux.
En plus d'??tre utilis?? pour d??crire, pr??dire et expliquer le comportement, la th??orie des jeux a ??galement ??t?? utilis?? pour d??velopper des th??ories de comportement ??thique ou normative et ?? prescrire un tel comportement. En l'??conomie et la philosophie, les chercheurs ont appliqu?? la th??orie des jeux pour aider ?? la compr??hension du comportement bon ou bon. La th??orie des jeux arguments de ce type peuvent ??tre trouv??s aussi loin que Platon .
Description et mod??lisation

La premi??re utilisation connue est de d??crire et mod??le comment les populations humaines se comportent. Certains ??rudits pensent que par trouver les ??quilibres de jeux qu'ils peuvent pr??dire comment les populations humaines r??elles se comportent lorsqu'ils sont confront??s ?? des situations analogues au jeu ?? l'??tude. Ce point de vue particulier de la th??orie des jeux a ??t?? critiqu??e r??cemment. Premi??rement, il est critiqu?? parce que les hypoth??ses formul??es par les th??oriciens des jeux sont souvent viol??s. Les th??oriciens des jeux peuvent prendre les joueurs agissent toujours de fa??on ?? maximiser directement leurs victoires (la mod??le de Homo economicus), mais dans la pratique, le comportement humain se ??carte souvent de ce mod??le. Explications de ce ph??nom??ne sont nombreuses; irrationalit??, de nouveaux mod??les de d??lib??ration, ou m??me des motifs diff??rents (comme celle de l'altruisme ). Les th??oriciens des jeux r??pondent en comparant leurs hypoth??ses ?? ceux utilis??s en physique. Ainsi, alors que leurs hypoth??ses ne tiennent pas toujours, ils peuvent traiter la th??orie des jeux comme un scientifique raisonnable apparent?? id??al pour les mod??les utilis??s par physiciens. Toutefois, dans le jeu de mille-pattes, deviner 2/3 du jeu moyenne, et le jeu du dictateur, les gens ne jouent pas r??guli??rement ??quilibres de Nash. Ces exp??riences ont d??montr?? que les individus ne jouent pas strat??gies d'??quilibre. Il ya un d??bat en cours sur l'importance de ces exp??riences.
Par ailleurs, certains auteurs affirment que les ??quilibres de Nash ne fournissent pas de pr??visions pour les populations humaines, mais plut??t fournir une explication pour pourquoi les populations qui jouent ??quilibres de Nash restent dans cet ??tat. Cependant, la question de la fa??on dont les populations atteignent ces points reste ouvert.
Certains th??oriciens de jeu se sont tourn??s vers la th??orie des jeux ??volutive afin de r??soudre ces questions. Ces mod??les supposent soit pas de rationalit?? ou rationalit?? limit??e de la part des joueurs. Malgr?? son nom, la th??orie des jeux ??volutionniste ne pr??sume pas n??cessairement la s??lection naturelle au sens biologique. La th??orie des jeux ??volutionniste comprend deux mod??les biologiques ainsi que l'??volution culturelle et aussi de l'apprentissage individuel (par exemple, dynamique de jeu fictifs).
Analyse prescriptive ou normative
| Coop??rer | D??faut | |
| Coop??rer | -1, -1 | -10, 0 |
| D??faut | 0, -10 | -5, -5 |
| Le dilemme du prisonnier | ||
D'autre part, certains sp??cialistes voient pas la th??orie de jeu un outil pr??dictif pour le comportement des ??tres humains, mais comme une suggestion de la fa??on dont les gens doivent se comporter. Depuis une strat??gie, correspondant ?? un ??quilibre de Nash d'un jeu constitue son meilleure r??ponse aux actions des autres joueurs - pour autant qu'elles soient (m??me) l'??quilibre de Nash -, jouant une strat??gie qui fait partie d'un ??quilibre de Nash semble appropri??. Cependant, la rationalit?? d'une telle d??cision a ??t?? prouv?? que pour les cas sp??ciaux. Cette utilisation normative de la th??orie des jeux a ??galement ??t?? critiqu??e. Premi??rement, dans certains cas, il convient de jouer une strat??gie de non-??quilibre si l'on se attend ?? d'autres de jouer des strat??gies non-??quilibre ainsi. Pour un exemple, voir deviner 2/3 de la moyenne.
Deuxi??mement, le dilemme du prisonnier pr??sente une autre contre-potentiel. Dans le dilemme du prisonnier, chaque joueur poursuivant son propre int??r??t conduit les deux joueurs d'??tre pire que se ils ne avaient poursuivi leurs propres int??r??ts.
??conomie et affaires
La th??orie des jeux est une m??thode importante utilis??e dans ??conomie math??matique et les entreprises pour mod??lisation des comportements concurrents d'interagir agents. Les applications incluent un large ??ventail de ph??nom??nes et des approches ??conomiques, tels que ventes aux ench??res, n??gociation, fusions et acquisitions prix, r??partition ??quitable, duopoles, oligopoles, formation de r??seaux sociaux, l'??conomie de calcul ?? base d'agents, ??quilibre g??n??ral, conception du m??canisme, et syst??mes de vote, et ?? travers ces zones aussi vastes que ??conomie exp??rimentale, l'??conomie comportementale , ??conomie de l'information, organisation industrielle et l'??conomie politique .
Cette recherche se concentre habituellement sur des ensembles particuliers de strat??gies connues comme ??quilibres dans les jeux. Ces ??concepts de solutions" sont g??n??ralement bas??es sur ce qui est requis par les normes de la rationalit??. Dans les jeux non-coop??ratifs, le plus c??l??bre d'entre eux est l' ??quilibre de Nash . Un ensemble de strat??gies est un ??quilibre de Nash si chacun repr??sente une meilleure r??ponse aux autres strat??gies. Donc, si tous les joueurs jouent les strat??gies dans un ??quilibre de Nash, ils ne ont aucune incitation unilat??rale de se ??carter, car leur strat??gie est le mieux qu'ils peuvent faire compte tenu de ce que font les autres.
Les gains du jeu sont g??n??ralement prises pour repr??senter la utilit?? des joueurs individuels. Souvent dans des situations de mod??lisation les gains repr??sentent de l'argent, ce qui correspond sans doute ?? l'utilit?? d'un individu. Cette hypoth??se, cependant, peut ??tre d??fectueux.
Un document prototype sur la th??orie des jeux en ??conomie commence par pr??senter un jeu qui est une abstraction d'une situation ??conomique particuli??re. Un ou plusieurs concepts de solution sont choisis, et l'auteur montre les jeux de strat??gie dans le jeu pr??sent?? ??quilibres sont du type appropri??. Naturellement on peut se demander ?? quoi sert cette information devrait ??tre mis. Les ??conomistes et professeurs d'affaires sugg??rent deux principales utilisations (ci-dessus): descriptif et prescriptive.
Science politique
L'application de la th??orie des jeux ?? la science politique se concentre dans les zones de chevauchement de partage ??quitable, l'??conomie politique , choix publics, n??gociation de guerre, la th??orie politique positif, et th??orie du choix social. Dans chacun de ces domaines, les chercheurs ont ??labor?? des mod??les de la th??orie des jeux dans lesquels les joueurs sont souvent les ??lecteurs, ??tats, groupes d'int??r??ts sp??ciaux, et des politiciens.
Pour les premiers exemples de la th??orie des jeux appliqu??e ?? la science politique, voir le travail de Anthony Downs. Dans son livre Une th??orie ??conomique de la d??mocratie (Downs 1957), il applique la Hotelling mod??le de localisation des entreprises dans le processus politique. Dans le mod??le de Downs, les candidats politiques se engagent ?? des id??ologies sur un espace politique unidimensionnelle. Downs premi??res montre comment les candidats politiques vont converger ?? l'id??ologie pr??f??r?? par l'??lecteur m??dian si les ??lecteurs soient pleinement inform??s, mais fait valoir que les ??lecteurs choisissent de rester ignorants rationnelle qui permet de divergence du candidat.
Une explication de la th??orie des jeux pour paix d??mocratique est que le d??bat public et ouvert dans les d??mocraties envoyer des informations claires et fiables sur leurs intentions ?? d'autres Etats. En revanche, il est difficile de conna??tre les intentions des dirigeants non d??mocratiques, ce concessions effet auront, et si promesses seront tenues. Ainsi il y aura la m??fiance et la r??ticence ?? faire des concessions si au moins une des parties ?? un diff??rend est un non-d??mocratie (Levy & Razin 2003).
Biologie
| Faucon | Colombe | |
| Faucon | 20, 20 | 80, 40 |
| Colombe | 40, 80 | 60, 60 |
| Le jeu faucon-colombe | ||
Les paiements pour les jeux en biologie , contrairement ?? ceux en ??conomie, sont souvent interpr??t??es comme correspondant ?? fitness. En outre, l'accent a ??t?? mis sur moins ??quilibres qui correspondent ?? une notion de rationalit?? et plus sur ceux qui seraient entretenus par l'??volution des forces. L'??quilibre le plus connu en biologie est connue comme la strat??gie ??volutionnaire stable (ou SST), et a ??t?? introduit en (Smith & Prix 1973). Bien que sa motivation initiale ne comportait aucune des exigences mentales de l' ??quilibre de Nash , chaque ESS est un ??quilibre de Nash.
En biologie, th??orie des jeux a ??t?? utilis??e pour comprendre de nombreux ph??nom??nes diff??rents. Il a ??t?? d'abord utilis?? pour expliquer l'??volution (et de la stabilit??) de la approximative de 1: 1 rapports sexuels. (Fisher 1930) a sugg??r?? que les 1: rapports de masculinit?? 1 sont le r??sultat de forces ??volutives qui agissent sur les personnes qui pourraient ??tre consid??r??es comme essayer de maximiser le nombre de leurs petits-enfants.
En outre, les biologistes ont utilis?? la th??orie des jeux de l'??volution et l'ESS pour expliquer l'??mergence de communication animale (Harper & Maynard Smith, 2003). L'analyse de jeux de signalisation et d'autres jeux de communication a permis de mieux comprendre l'??volution de la communication chez les animaux. Par exemple, le mobbing comportement de nombreuses esp??ces, dont un grand nombre d'animaux de proie attaque un pr??dateur plus grand, semble ??tre un exemple d'organisation ??mergente spontan??e. Les fourmis ont ??galement ??t?? montr?? pour pr??senter un comportement de feed-forward se apparente ?? la mode, voir Economie papillon.
Les biologistes ont utilis?? le jeu de poulet pour analyser le comportement des combats et de la territorialit??.
Maynard Smith, dans la pr??face de l'??volution et la th??orie des jeux, ??crit: ??paradoxalement, il se est av??r?? que la th??orie des jeux est plus facilement appliqu?? ?? la biologie que de le domaine du comportement ??conomique pour laquelle il a ??t?? con??u ?? l'origine". La th??orie des jeux ??volutionniste a ??t?? utilis??e pour expliquer de nombreux ph??nom??nes apparemment incongrues dans la nature.
Un tel ph??nom??ne est appel?? altruisme biologique. Ce est une situation dans laquelle l'organisme semble agir d'une mani??re qui b??n??ficie d'autres organismes et est pr??judiciable ?? lui-m??me. Ce est distinct des notions traditionnelles de l'altruisme parce que ces actions ne sont pas conscients, mais semblent ??tre adaptations ??volutives pour augmenter la condition physique g??n??rale. Des exemples peuvent ??tre trouv??s dans les esp??ces allant de chauves-souris vampires qui r??gurgitent sang qu'ils ont obtenu de la chasse de nuit et lui donnent aux membres du groupe qui ne ont pas pour se nourrir, pour les abeilles ouvri??res qui se occupent de la reine pendant toute leur vie et ne jamais se accouplent, ?? singes vervets qui avertissent les membres du groupe de l'approche d'un pr??dateur, m??me si elle met en danger les chances de survie de cette personne. Toutes ces actions augmenter la condition physique g??n??rale d'un groupe, mais se produisent ?? un co??t pour l'individu.
La th??orie des jeux ??volutionniste explique cet altruisme avec l'id??e de la s??lection de parent??le. Altruistes discrimination entre les personnes qu'ils aident et parents de faveur. La r??gle de Hamilton explique le raisonnement derri??re cette ??volution s??lection avec l'??quation c La th??orie des jeux est venu ?? jouer un r??le plus important dans la logique et la science informatique . Plusieurs th??ories logiques aient une base la s??mantique des jeux. En outre, les informaticiens ont utilis?? des jeux pour mod??liser calculs interactifs. En outre, la th??orie des jeux fournit une base th??orique pour le domaine de la syst??mes multi-agents. S??par??ment, la th??orie des jeux a jou?? un r??le dans algorithmes ligne. En particulier, la probl??me k-serveur, qui a dans le pass?? ??t?? appel?? jeux avec les frais de d??m??nagement et jeux demande-r??ponse (Ben David, Borodine et Karp et al., 1994). Le principe de Yao est une technique de la th??orie des jeux pour prouver des bornes inf??rieures sur le complexit?? de calcul randomis?? algorithmes, et surtout des algorithmes en ligne. L'??mergence de l'Internet a motiv?? le d??veloppement d'algorithmes pour trouver les ??quilibres dans les jeux, des march??s, des ventes aux ench??res de calcul, syst??mes peer-to-peer, et les march??s de s??curit?? et d'information. La th??orie des jeux algorithmique et en son sein conception du m??canisme de calcul algorithmique combiner conception et l'analyse de l'algorithme syst??mes complexes avec la th??orie ??conomique. La th??orie des jeux a ??t?? mis ?? plusieurs usages dans la philosophie . R??pondant ?? deux articles par WVO Quine (1960, 1967), Lewis (1969) a utilis?? la th??orie des jeux pour d??velopper un compte philosophique de convention. Ce faisant, il a fourni la premi??re analyse des connaissances communes et employ?? dans l'analyse de jeu dans jeux de coordination. En outre, il a d'abord sugg??r?? que l'on peut comprendre ce qui signifie en termes de jeux de signalisation. Cette suggestion a ??t?? plus tard poursuivi par plusieurs philosophes depuis Lewis (Skyrms (1996), Grim, Kokalis et Alai-Tafti et al. (2004)). Apr??s Lewis (1969) la th??orie des jeux compte des conventions, Edna Ullmann-Margalit (1977) et Verres (2006) ont d??velopp?? des th??ories de les normes sociales qui les d??finissent comme des ??quilibres de Nash qui r??sultent de la transformation d'un jeu mixte mobile dans un jeu de coordination. La th??orie des jeux a ??galement contest?? philosophes ?? penser en termes de interactive ??pist??mologie: ce que cela signifie pour un collectif d'avoir des croyances ou des connaissances communes, et quelles sont les cons??quences de cette connaissance pour les r??sultats sociaux r??sultant des interactions entre agents. Les philosophes qui ont travaill?? dans ce domaine comprennent Bicchieri (1989, 1993), Skyrms (1990), et Stalnaker (1999). Dans l'??thique , certains auteurs ont tent?? de poursuivre le projet, commenc?? par Thomas Hobbes , de la morale d??coulant de l'int??r??t. Depuis les jeux comme le dilemme du prisonnier pr??senter un conflit apparent entre la morale et l'int??r??t, en expliquant pourquoi la coop??ration est requise par l'int??r??t personnel est une composante importante de ce projet. Cette strat??gie g??n??rale est un composant de la g??n??rale vue contrat social en philosophie politique (pour des exemples, voir Gauthier (1986) et Kavka (1986). D'autres auteurs ont tent?? d'utiliser la th??orie des jeux ??volutionniste pour expliquer l'??mergence d'attitudes humaines sur la moralit?? et les comportements des animaux correspondantes. Ces auteurs se penchent sur plusieurs jeux, y compris le dilemme du prisonnier, chasse au cerf, et la Nash jeu de n??gociation en fournissant une explication de l'??mergence d'attitudes sur la moralit?? (voir, par exemple, Skyrms (1996, 2004) et Sober et Wilson (1999)). Certaines hypoth??ses utilis??es dans certaines parties de la th??orie des jeux ont ??t?? contest??es dans la philosophie; par exemple, l'??go??sme psychologique indique que la rationalit?? se r??duit ?? l'auto-int??r??t une r??clamation d??battue parmi les philosophes. (Voir L'??go??sme psychologique # de critiques) Un jeu est coop??ratif si les joueurs sont capables de former des engagements contraignants. Par exemple, le syst??me juridique les oblige ?? respecter leurs promesses. Dans les jeux non coop??ratifs ce ne est pas possible. Souvent, il est suppos?? que la communication entre les joueurs est autoris?? dans des jeux coop??ratifs, mais pas dans ceux non coop??ratifs. Cependant, cette classification sur deux crit??res binaires a ??t?? remise en question, et parfois rejet?? (Harsanyi 1974). Parmi les deux types de jeux, jeux non coop??ratifs sont capables de mod??liser des situations dans les moindres d??tails, produisant des r??sultats pr??cis. Jeux coop??ratifs se concentrent sur le jeu en g??n??ral. Des efforts consid??rables ont ??t?? d??ploy??s pour relier les deux approches. Le soi-disant Nash-programme a d??j?? mis en place un grand nombre de solutions concert??es ??quilibres non coop??ratifs. Jeux hybrides contiennent des ??l??ments coop??ratifs et non coop??ratifs. Par exemple, les coalitions de joueurs sont form??s dans un jeu coop??ratif, mais ce jeu de fa??on non-coop??rative. Un jeu sym??trique est un jeu o?? les gains pour jouer une strat??gie particuli??re ne d??pendent que sur les autres strat??gies employ??es, non pas sur qui est de les jouer. Si l'identit?? des joueurs peuvent ??tre modifi??s sans changer le gain aux strat??gies, puis un jeu est sym??trique. Beaucoup des couramment ??tudi??es 2 ?? 2 jeux sont sym??triques. Les repr??sentations standard de poulet, la dilemme du prisonnier, et de la chasse au cerf sont tous les jeux sym??triques. Certains chercheurs envisageraient certains jeux asym??triques comme exemples de ces jeux ainsi. Toutefois, les gains les plus courantes pour chacun de ces jeux sont sym??triques. Le plus souvent asym??triques jeux ??tudi??s sont des jeux o?? il ne sont pas des ensembles de strat??gies identiques pour les deux joueurs. Par exemple, le jeu de l'ultimatum et de m??me la jeu du dictateur ont des strat??gies diff??rentes pour chaque joueur. Il est possible, cependant, pour un jeu d'avoir des strat??gies identiques pour les deux joueurs, mais ??tre asym??trique. Par exemple, le jeu sur la photo ?? droite est asym??trique malgr?? des ensembles de strat??gies identiques pour les deux joueurs. Jeux ?? somme nulle sont un cas particulier de jeux ?? somme constante, dans lequel les choix par les joueurs ne peut ni augmenter ni diminuer les ressources disponibles. Dans les jeux ?? somme nulle l'avantage total ?? tous les joueurs dans le jeu, pour chaque combinaison de strat??gies, ajoute toujours ?? z??ro (plus informelle, un joueur b??n??ficie seulement aux d??pens ??gale des autres). Poker illustre un jeu ?? somme nulle (en ignorant la possibilit?? de la coupe de la maison), parce que l'on gagne exactement le montant ses adversaires perdent. Autres jeux ?? somme nulle comprennent correspondant centimes et la plupart des jeux de soci??t?? classiques y compris Go et d'??checs . Beaucoup de jeux ??tudi??s par les th??oriciens des jeux (y compris l'inf??me dilemme du prisonnier) sont des jeux non ?? somme nulle, parce que la r??sultat net a des r??sultats sup??rieurs ou inf??rieurs ?? z??ro. Officieusement, dans les jeux non ?? somme nulle, un gain par un joueur ne correspond pas n??cessairement ?? une perte par un autre. Jeux ?? somme constante correspondent ?? des activit??s comme le vol et le jeu, mais pas ?? la situation ??conomique fondamentale dans laquelle il ya un potentiel gains tir??s du commerce. Il est possible de transformer ne importe quel jeu dans un (??ventuellement asym??trique) jeu ?? somme nulle en ajoutant un joueur fictif suppl??mentaire (souvent appel?? le ??Conseil??), dont les pertes de compenser les gains nets des joueurs. Jeux simultan??s sont des jeux o?? les deux joueurs se d??placent simultan??ment, ou se ils ne se d??placent pas en m??me temps, les joueurs ult??rieures ne sont pas conscients des actions des joueurs pr??c??dents (ce qui les rend efficace simultan??e). Jeux s??quentiels (ou dynamiques) jeux sont des jeux o?? les joueurs plus tard ont une certaine connaissance sur les actions ant??rieures. Ce ne doit pas ??tre information parfaite sur chaque action de joueurs ant??rieures; il pourrait ??tre tr??s peu de connaissances. Par exemple, un joueur peut savoir que un joueur plus t??t n'a pas effectu?? une action particuli??re, alors qu'il ne sait pas lequel des autres actions disponibles le premier joueur r??ellement effectu??. La diff??rence entre les jeux s??quentiels simultan??s et est captur??e dans les diff??rentes repr??sentations d??crites ci-dessus. Souvent, forme normale est utilis??e pour repr??senter des parties simultan??es, et forme extensive est utilis??e pour repr??senter s??quentielles. La transformation du vaste sous forme normale est une fa??on, ce qui signifie que plusieurs vastes jeux de forme correspondent ?? la m??me forme normale. Par cons??quent, notions d'??quilibre pour les jeux simultan??s sont insuffisantes pour raisonner sur les jeux s??quentiels; voir la perfection en sous-jeux. En bref, les diff??rences entre s??quentiel et jeux simultan??s sont les suivantes: Un important sous-ensemble de jeux s??quentiels se compose de jeux de information parfaite. Un jeu est l'une des informations parfait si tous les joueurs connaissent les mouvements pr??c??demment par tous les autres joueurs. Ainsi, seuls les jeux s??quentiels peuvent ??tre des jeux de l'information parfaite parce que les joueurs dans les jeux simultan??s ne connaissent pas les actions des autres joueurs. La plupart des jeux ??tudi??s dans la th??orie des jeux sont des jeux imparfaite-information. Des exemples int??ressants de jeux parfaite-information comprennent le jeu de l'ultimatum et jeu de mille-pattes. Jeux de loisirs de parfaits jeux d'information comprennent les ??checs , aller et mancala . Beaucoup de jeux de cartes sont des jeux de l'information imparfaite, par exemple poker ou Bridge. Information parfaite est souvent confondue avec des informations compl??tes, qui est un concept similaire. Une information compl??te n??cessite que chaque joueur de conna??tre les strat??gies et les paiements disponibles pour les autres joueurs, mais pas n??cessairement les actions prises. Jeux d'informations incompl??tes peuvent ??tre r??duits, cependant, aux jeux de l'information imparfaite en introduisant " se d??place par nature "(Leyton-Brown & Shoham 2008, p. 60). Jeux o?? la difficult?? de trouver une strat??gie optimale provient de la multiplicit?? des coups possibles sont appel??s jeux combinatoires. Les exemples incluent les ??checs et viennent. Jeux qui impliquent une information imparfaite ou incompl??te peuvent ??galement avoir un fort caract??re combinatoire, par exemple backgammon . Il n'y a aucune th??orie unifi??e des ??l??ments d'adressage dans les jeux combinatoires. Il ya, cependant, des outils math??matiques qui peuvent r??soudre des probl??mes particuliers et r??pondre aux questions g??n??rales. Jeux de l'information parfaite ont ??t?? ??tudi??s dans la th??orie des jeux combinatoires, qui a d??velopp?? de nouvelles repr??sentations, par exemple num??ros surr??aliste, ainsi que combinatoire et alg??brique (et parfois non-constructives) m??thodes de preuve r??soudre les jeux de certains types, y compris les jeux "boucl??es" qui peuvent r??sulter en une infinit?? de longues s??quences de mouvements. Ces m??thodes se adressent jeux avec la complexit?? combinatoire sup??rieur ?? ceux habituellement pris en compte dans la th??orie traditionnelle (ou ????conomique??) jeu. Un jeu typique qui a ??t?? r??solu de cette fa??on est hex. Un domaine d'??tude connexe, puisant th??orie de la complexit?? de calcul, est la complexit?? du jeu, qui est concern?? par l'estimation de la difficult?? de calcul de trouver des strat??gies optimales. Research in l'intelligence artificielle a abord?? deux jeux parfaits et imparfaits (ou incompl??tes) l'information qui ont des structures combinatoires tr??s complexes (comme les ??checs, go, backgammon ou) pour lesquels aucune des strat??gies optimales prouvables ont ??t?? trouv??s. Les solutions pratiques impliquent heuristiques de calcul, comme ??lagage alpha-b??ta ou l'utilisation de r??seaux de neurones artificiels form??s par apprentissage par renforcement, ce qui rend les jeux plus docile dans la pratique de l'informatique. Jeux, comme ??tudi?? par les ??conomistes et les joueurs du monde r??el, sont g??n??ralement termin?? en un nombre fini de mouvements. Math??maticiens purs ne sont pas ainsi restreints, et mis th??oriciens en particulier les jeux de l'??tude qui durent une infinit?? de mouvements, avec le gagnant (ou autre gain) non connus qu'apr??s tous ces mouvements sont termin??s. L'attention est g??n??ralement pas tellement sur ce qui est la meilleure fa??on de jouer un tel jeu, mais simplement de savoir si l'un ou l'autre joueur a une strat??gie gagnante. (Il peut ??tre prouv??, en utilisant le axiome du choix, qu'il ya des jeux-m??me avec une information parfaite, et o?? les seuls r??sultats sont ??gagner?? ou ??perdre?? -pour laquelle ni joueur a une strat??gie gagnante.) L'existence de ces strat??gies, pour les jeux con??us intelligemment, a cons??quences importantes la th??orie des ensembles descriptive. Une grande partie de la th??orie des jeux est toutefois pr??occup?? avec des jeux finis discrets, qui ont un nombre fini de joueurs, des mouvements, des ??v??nements, r??sultats, etc. Beaucoup de concepts peuvent ??tre prorog??s,. Jeux en continu permettent aux joueurs de choisir une strat??gie d'un jeu de strat??gie continue. Par exemple, Concurrence ?? la Cournot est g??n??ralement mod??lis?? avec les strat??gies des joueurs ??tant les quantit??s non n??gatifs, y compris les quantit??s fractionnaires. Jeux diff??rentiels comme le continu poursuite et ??vasion jeu sont des jeux continus o?? l'??volution des variables d'??tat des joueurs est r??gi par des ??quations diff??rentielles . Le probl??me de trouver une strat??gie optimale dans un jeu diff??rentiel est ??troitement li??e ?? la th??orie du contr??le optimal. En particulier, il existe deux types de strat??gies: les strat??gies en boucle ouverte sont trouv??s en utilisant le Pontryagin principe du maximum tandis que les strat??gies en boucle ferm??e sont trouv??s en utilisant M??thode de programmation dynamique de Bellman. Un cas particulier de jeux diff??rentiels sont les jeux disposant d'un horizon de temps al??atoire. Dans ces jeux, le temps terminal est une variable al??atoire avec une donn??e distribution de probabilit?? fonction. Par cons??quent, les joueurs de maximiser la esp??rance math??matique de la fonction de co??t. Il a ??t?? montr?? que le probl??me d'optimisation modifi?? peut ??tre reformul?? comme un jeu diff??rentiel actualis??s sur un intervalle de temps infini. Jeux avec un arbitraire, mais finie, nombre de joueurs sont souvent appel??s jeux n-personne (Luce & Raiffa 1957). La th??orie des jeux ??volutionniste consid??re jeux impliquant une population de d??cideurs, o?? la fr??quence avec laquelle une d??cision particuli??re est faite peut changer avec le temps en r??ponse aux d??cisions prises par tous les individus de la population. En biologie, ce est destin?? ?? mod??liser (biologique) ??volution , o?? les organismes g??n??tiquement programm??s passent le long de certaines de leurs ??missions de strat??gie pour leur prog??niture.En économie, la même théorie est destiné à capturer les changements de population parce que les gens jouent le jeu de fois dans leur vie, et consciemment (et peut-être rationnellement) les stratégies de commutation (Webb, 2007). Probl??mes de d??cision individuelles avec les r??sultats stochastiques sont parfois consid??r??s comme des ??jeux d'un joueur". Ces situations ne sont pas considérés jeu théorique par certains auteurs. Ils peuvent être modélisées en utilisant des outils similaires au sein des disciplines connexes de la théorie de la décision, la recherche opérationnelle et les domaines de l'intelligence artificielle, en particulier la planification AI (l'incertitude) et système multi-agents. Bien que ces domaines peuvent avoir différents facteurs de motivation, les mathématiques impliquées sont sensiblement les mêmes, par exemple en utilisant des processus de décision de Markov (MDP). Résultats stochastiques peuvent également être modélisés en termes de théorie de jeu en ajoutant un joueur agissant au hasard qui fait "se déplace de chance», aussi connu comme " mouvements de la nature »(Osborne & Rubinstein, 1994). Ce joueur est généralement pas considéré comme un troisième joueur dans ce qui est autrement un jeu à deux joueurs, mais sert simplement à fournir un coup de dés où requis par le jeu. Pour certains problèmes, différentes approches de modélisation stochastiques résultats peuvent conduire à des solutions différentes. Par exemple, la différence d'approche entre les CMD et la solution minimax est que ce dernier considère le pire des cas sur un ensemble de mouvements contradictoires, plutôt que le raisonnement dans l'attente de ces mouvements donnés une distribution de probabilité fixe. L'approche minimax peut être avantageux où les modèles stochastiques d'incertitude ne sont pas disponibles, mais peut également être surestime événements extrêmement improbables (mais coûteux), se balançant de façon spectaculaire la stratégie dans de tels scénarios, si on suppose que l'adversaire peut forcer un tel événement se produise. (Voir théorie du cygne noir pour plus de discussion sur ce genre de question de modélisation, particulièrement en ce qui a trait à prédire et limiter les pertes dans la banque d'investissement.) Modèles généraux qui incluent tous les éléments de résultats stochastiques, adversaires, et observabilité partielle ou bruyant (de coups par d'autres joueurs) ont également été étudiés. La " règle d'or "est considéré comme partiellement observable jeu stochastique (de POSG), mais quelques problèmes sont réalistes calcul est possible dans la représentation POSG. Ce sont des jeux dont le jeu est le développement des règles pour un autre jeu, la cible ou l'objet jeu. Metagames cherchent à maximiser la valeur d'utilité de l'ensemble de règles développées. La théorie de Metagames est liée à la théorie de la conception du mécanisme. Le terme analyse metagame est également utilisé pour faire référence à une approche pratique développé par Nigel Howard (Howard, 1971) dans lequel une situation est encadrée comme un jeu stratégique dans lequel les parties prenantes tentent de réaliser leurs objectifs par le biais des options à leur disposition. Les développements ultérieurs ont conduit à la formulation de l'analyse de la confrontation. Les premières discussions d'exemples de jeux à deux eu lieu bien avant l'avènement de la théorie des jeux modernes, mathématique. La discussion a d'abord connu de la théorie des jeux a eu lieu dans une lettre écrite par James Waldegrave en 1713. Dans cette lettre, Waldegrave fournit une minimax solution de stratégie mixte à une version de deux personnes du jeu de carte le Son. James Madison a fait ce que nous reconnaissons maintenant que une analyse de la théorie des jeux des façons états peut être devrait se comporter sous différents systèmes d'imposition. Dans son 1838 Recherches sur les Principes mathématiques de la théorie des richesses ( Recherches sur les principes mathématiques de la théorie des richesses ), Antoine Augustin Cournot considéré comme un duopole et présente une solution qui est une version restreinte de l' équilibre de Nash . Le mathématicien danois Zeuthen prouvé que le modèle mathématique a une stratégie gagnante en utilisant théorème de point fixe de Brouwer. Dans ses 1938 livres Applications aux Jeux de Hasard et notes antérieures, Émile Borel prouvé un théorème minimax pour deux personnes jeux de matrice à somme nulle que lorsque la matrice de pay-off était symétrique. Borel a conjecturé que la non-existence d'équilibres en stratégies mixtes dans deux personnes jeux à somme nulle aurait lieu, une conjecture qui a été prouvé faux. La théorie des jeux n'a pas vraiment exister comme un champ unique jusqu'à ce que John von Neumann a publié un document en preuve originale de 1928. Von Neumann utilisée point fixe le théorème de Brouwer sur applications continues en ensembles convexes compacts, qui est devenue une méthode standard dans la théorie des jeux et de l'économie mathématique. Son document a ??t?? suivi par son livre 1944 Théorie des Jeux et le comportement économique . La deuxième édition de ce livre a fourni une théorie axiomatique de l'utilité, qui réincarne vieille théorie de Daniel Bernoulli d'utilité (de l'argent) en tant que discipline indépendante. Les travaux de Von Neumann en théorie des jeux a culminé dans ce livre 1944. Ce travail de base contient la méthode pour trouver des solutions mutuellement cohérentes pour deux personnes jeux à somme nulle. Au cours de la période suivante, les travaux sur la théorie des jeux est principalement axé sur la théorie des jeux coopératifs, qui analyse les stratégies optimales pour des groupes d'individus, en supposant qu'ils peuvent appliquer les accords entre eux sur les stratégies appropriées. En 1950, la première discussion mathématique du dilemme du prisonnier est apparu, et une expérience a été menée par les mathématiciens notables Merrill M. Flood et Melvin Dresher, dans le cadre de l' enquêtes de RAND corporation dans la théorie des jeux. Rand a poursuivi les études en raison d'applications possibles au global la strat??gie nucl??aire. autour de ce même temps, John Nash ont développé un critère de cohérence mutuelle des stratégies des acteurs, connus comme l'équilibre de Nash, applicable à une plus grande variété de jeux que le critère proposé par von Neumann et Morgenstern. Cet équilibre est suffisamment général pour permettre l'analyse de jeux non-coopératifs en plus de ceux de coopération. La théorie des jeux a connu un regain d'activité dans les années 1950, période durant laquelle les concepts de l' âme, la forme extensive jeu, jeu fictif, jeux répétés, et la valeur de Shapley ont été développés. En outre, les premières applications de la théorie des jeux à la philosophie et la science politique ont eu lieu pendant cette période. En 1965, Reinhard Selten a présenté son concept de solution de sous-jeu parfait équilibre, qui a encore affiné l'équilibre de Nash (plus tard, il serait introduire tremblante perfection de main aussi bien). En 1967, John Harsanyi a développé les concepts d' une information complète et jeux bayésiens. Nash, Selten et Harsanyi devenus lauréats du prix Nobel d'économie en 1994 pour ses contributions à la théorie de jeu économique. Dans les années 1970, la théorie des jeux a été largement appliquée dans la biologie , en grande partie en raison du travail de John Maynard Smith et sa stratégie évolutivement stable . En outre, les concepts de l'équilibre corrélé, la perfection de la main tremblante, et la connaissance commune ont été présentés et analysés. En 2005, les théoriciens de jeu Thomas Schelling et Robert Aumann suivies Nash, Selten et Harsanyi comme lauréats du prix Nobel. Schelling a travaillé sur des modèles dynamiques, les premiers exemples de la théorie des jeux évolutionniste. Aumann plus contribué à l'école d'équilibre, l'introduction d'un grossissement d'équilibre, l'équilibre corrélé, et de développer un vaste analyse formelle de l'hypothèse de la connaissance commune et de ses conséquences. En 2007, Leonid Hurwicz, avec Eric Maskin et Roger Myerson, a reçu le prix Nobel d'économie "pour avoir jeté les bases de la théorie de la conception du mécanisme. " Les contributions de Myerson comprennent la notion de juste équilibre, et un texte d'études supérieures importante: la théorie des jeux, Analyse des conflits (Myerson 1997). Hurwicz introduit et formalisé le concept de compatibilité des incitations. L'histoire de la vie du jeu théoricien et mathématicienJohn Nash a été transformé en un biopic, A Beautiful Mindmettant en vedetteRussell Crowe, basé sur le livre deSylvia Nasar. "Jeux-théorie» et «théorie des jeux» sont mentionnés dans le roman de science fiction militaire Starship Troopers par Robert A. Heinlein. Dans le film du même nom 1997, le caractère Carl Jenkins se réfère à sa mission, le renseignement militaire, comme des «jeux et la théorie." L'un des principaux gameplay de décision mécanique du jeu vidéo évasion Zero: Dernière récompense de la vertu est fondée sur la théorie des jeux. Certains des personnages référence, même le dilemme du prisonnier. Le film Dr. Strangelove satire jeu idées théoriques à propos de la théorie de la dissuasion. Par exemple, la dissuasion nucléaire dépend de la menace de représailles catastrophique si une attaque nucléaire est détectée. Un théoricien des jeux pourrait faire valoir que ces menaces peuvent manquer d'être crédible , dans le sens où ils peuvent conduire à sous-jeu des équilibres imparfaits. Le film prend cette idée un peu plus loin, avec les Russes commettre irrévocablement à une réponse nucléaire catastrophique sans faire le public de la menace. Informatique et logique
Philosophie
Cerf Li??vre
Cerf 3, 3 0, 2 Li??vre 2, 0 2, 2 Stag chasse Types de jeux
Coop??rative ou non coop??rative
Sym??trique et asym??trique
E Fa E 1, 2 0, 0 Fa 0, 0 1, 2 Un jeu asym??trique ?? somme nulle et non ?? somme nulle
Un B Un -1, 1 3, -3 B 0, 0 -2, 2 Un jeu ?? somme nulle Simultan??e et s??quentielle
S??quentiel Simultan?? Normalement d??sign?? par: Arbres de d??cision Matrices Payoff La connaissance pr??alable du d??m??nagement de l'adversaire: Oui Aucun Temps Axe: Oui Aucun Aussi connu comme: Jeu vaste Jeu strat??gique Information parfaite et d'information imparfaite

![]()
Jeux combinatoires
Infiniment longs jeux
Jeux discrets et continus
jeux diff??rentielles
Beaucoup-joueur et les jeux de la population
Résultats stochastiques (et par rapport aux autres domaines)
Metagames
Histoire
La culture populaire

