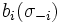??quilibre de Nash
Renseignements g??n??raux
Enfants SOS ont produit une s??lection d'articles de wikipedia pour les ??coles depuis 2005. Parrainer un enfant de faire une r??elle diff??rence.
| ??quilibre de Nash | |
|---|---|
| Un concept de solution dans la th??orie des jeux | |
| Relations | |
| Sous-ensemble de | Rationalizability, Epsilon-??quilibre, ??quilibre corr??l?? |
| Superset de | Evolutionarily strat??gie stable , Sous-jeu parfait ??quilibre, L'??quilibre parfait bayesien, Main tremblante ??quilibre parfait |
| Importance | |
| Propos?? par | John Forbes Nash |
| Utilis?? pour | Tous jeux non-coop??ratifs |
| Exemple | Dilemme du prisonnier |
Dans la th??orie des jeux , l'??quilibre de Nash (nomm?? d'apr??s John Forbes Nash, qui l'a propos??e) est un concept de solution d'un jeu impliquant deux joueurs ou plus, dans lequel aucun joueur n'a rien ?? gagner en changeant seulement son propre strat??gie unilat??ralement. Si chaque joueur a choisi une strat??gie et aucun joueur ne peut b??n??ficier en modifiant sa strat??gie alors que les autres joueurs gardent leur inchang??e, alors l'ensemble actuel de choix strat??giques et les gains correspondants constitue un ??quilibre de Nash.
En termes simples, Amy et le projet de loi sont en ??quilibre de Nash si Amy fait la meilleure d??cision qu'elle peut, en tenant compte de la d??cision du projet de loi, et le projet de loi fait la meilleure d??cision qu'il peut, en tenant compte de la d??cision de Amy. De m??me, beaucoup de joueurs sont en ??quilibre de Nash si chacun fait la meilleure d??cision qu'ils peuvent, en tenant compte des d??cisions des autres. Cependant, l'??quilibre de Nash ne signifie pas n??cessairement le meilleur gain cumul?? pour tous les acteurs concern??s; dans de nombreux cas, tous les joueurs peuvent am??liorer leurs gains se ils ??taient en accord sur des strat??gies diff??rentes de l'??quilibre de Nash (par exemple, les hommes d'affaires. concurrentes formant une entente afin d'augmenter leurs profits).
Histoire
Le concept de l'??quilibre de Nash (NE) ne est pas tout ?? fait originale de Nash (par exemple, Antoine Augustin Cournot a montr?? comment trouver ce que nous appelons maintenant l'??quilibre de Nash de la Cournot jeu de duopole). Par cons??quent, certains auteurs se r??f??rent ?? lui comme un ????quilibre de Cournot-Nash" (ou comme un ????quilibre de Nash-Cournot"). Cependant, Nash a montr?? pour la premi??re fois dans sa th??se, des jeux non-coop??ratifs (1950), que les ??quilibres de Nash (en strat??gies mixtes) doit exister pour tous les jeux finis avec ne importe quel nombre de joueurs. Avant les travaux de Nash, ce ne avait ??t?? prouv??e pour deux joueurs jeux ?? somme nulle (par John von Neumann et Oskar Morgenstern en 1947).
D??finitions
D??finition informelle
Officieusement, un ensemble de strat??gies est un ??quilibre de Nash si aucun joueur ne peut faire mieux en changeant unilat??ralement sa strat??gie. Comme une heuristique, on peut imaginer que chaque joueur est dit les strat??gies des autres joueurs. Si ne importe quel joueur voudrait faire quelque chose de diff??rent apr??s avoir ??t?? inform?? sur les strat??gies des autres, alors ce jeu de strat??gies ne est pas un ??quilibre de Nash. Si, toutefois, le joueur ne veut pas passer (ou est indiff??rent entre commutation et pas), puis l'ensemble des strat??gies est un ??quilibre de Nash.
Cela peut avoir des cons??quences contre-intuitives. Depuis l'??quilibre de Nash se concentre sur les pr??f??rences d'un individu, ??tant donn?? que les autres gardent leurs choix fix??s, il peut y avoir des ??quilibres de Nash o??, si les joueurs pourraient coordonner, ils seraient tous veulent passer. Le chasse cerf pr??sente un exemple de ce ph??nom??ne.
D??finition formelle
Soit (S, F) est un jeu, o?? S est l'ensemble des profils de strat??gies et F est l'ensemble des profils de gain. Laisser  un profil de strat??gies de tous les joueurs, sauf pour le joueur
un profil de strat??gies de tous les joueurs, sauf pour le joueur  . Lorsque chaque joueur
. Lorsque chaque joueur 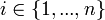 choisit la strat??gie
choisit la strat??gie 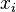 r??sultant du profil de strat??gie
r??sultant du profil de strat??gie 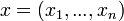 alors le joueur
alors le joueur  obtient gain
obtient gain 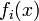 . Notez que le gain d??pend du profil de strat??gie choisie, ce est ?? dire sur la strat??gie choisie par le joueur
. Notez que le gain d??pend du profil de strat??gie choisie, ce est ?? dire sur la strat??gie choisie par le joueur  ainsi que les strat??gies choisies par tous les autres joueurs. Un profil de la strat??gie
ainsi que les strat??gies choisies par tous les autres joueurs. Un profil de la strat??gie  est un ??quilibre de Nash (NE) si aucune d??viation dans la strat??gie unilat??rale par un seul joueur est rentable, ce est-
est un ??quilibre de Nash (NE) si aucune d??viation dans la strat??gie unilat??rale par un seul joueur est rentable, ce est-
Un jeu peut avoir un NE pur de strat??gie ou un NE dans son l'extension mixte (celui de choisir une strat??gie pure stochastique avec un fixe fr??quence). Nash a prouv?? que, si nous permettons strat??gies mixtes (les joueurs choisissent des strat??gies au hasard, selon les probabilit??s pr??-attribu??), puis tous les n-joueur jeu dans lequel chaque joueur peut choisir parmi un nombre fini de strat??gies admet au moins un ??quilibre de Nash.
Exemples
jeu de la concurrence
| 0 'joueur choisit 2 | De 1 'joueur choisit 2 | De 2 'joueur choisit 2 | De 3 'joueur choisit 2 | |
|---|---|---|---|---|
| 0 '1 joueur choisit | 0, 0 | 2, -2 | 2, -2 | 2, -2 |
| De 1 'joueur choisit une | -2, 2 | 1, 1 | 3, -1 | 3, -1 |
| De 2 'joueur choisit une | -2, 2 | -1, 3 | 2, 2 | 4, 0 |
| De 3 'joueur choisit une | -2, 2 | -1, 3 | 0, 4 | 3, 3 |
Ceci peut ??tre illustr?? par un jeu ?? deux joueurs dans lequel les deux joueurs choisissent simultan??ment un nombre entier de 0 ?? 3 et ils ont tous deux gagner le plus petit des deux nombres en points. En outre, si un joueur choisit un nombre plus grand que l'autre, alors il / elle doit abandonner deux points ?? l'autre. Ce jeu a un unique ??quilibre de Nash: les deux joueurs choisissent 0 (surlign?? en rouge clair). Tout autre choix de strat??gies peut ??tre am??lior??e si l'un des joueurs abaisse son num??ro ?? un de moins que le num??ro de l'autre joueur. Dans le tableau ?? gauche, par exemple, lorsque commence sur la place verte, il est dans l'int??r??t du joueur 1 pour passer au carr?? violet en choisissant un plus petit nombre, et il est dans l'int??r??t du joueur 2 pour passer ?? la carr?? bleu en choisissant un plus petit nombre. Si le jeu est modifi??e de sorte que les deux joueurs gagnent le montant indiqu?? si les deux choisissent le m??me nombre, et sinon rien gagner, alors il ya 4 ??quilibres de Nash (0,0 ... 1,1 ... 2,2. ..et 3,3).
jeu de coordination
| Joueur 2 adopte une strat??gie 1 | Joueur 2 adopte une strat??gie 2 | |
|---|---|---|
| Joueur 1 adopte une strat??gie 1 | UN UNE DES | B, C |
| Joueur 1 adopte une strat??gie 2 | C, B | D, D |
Le jeu de coordination est un classique ( sym??trique) deux joueurs, deux jeu de strat??gie, avec le matrice des gains indiqu?? ?? droite, o?? les gains satisfont A> C et D> B. Les joueurs doivent donc coordonner, soit sur A ou sur D, pour recevoir une rentabilit?? ??lev??e. Si les choix des joueurs ne co??ncident pas, un paiement inf??rieur est r??compens??. Un exemple d'un jeu de coordination est le milieu o?? deux technologies sont disponibles pour deux entreprises avec des produits compatibles, et ils doivent ??lire une strat??gie visant ?? devenir le standard du march??. Si les deux entreprises se entendent sur la technologie choisie, les ventes ??lev??s sont attendus pour les deux entreprises. Si les entreprises ne se entendent pas sur la technologie standard, le r??sultat de quelques ventes. Les deux strat??gies sont ??quilibres de Nash du jeu.
Sur une route, et d'avoir ?? choisir soit de conduire sur la gauche ou de conduire sur le droit de la route, est aussi un jeu de coordination. Par exemple, avec 100 gains sens pas de crash et 0 signifie un accident, le jeu de coordination peut ??tre d??finie avec la matrice de gain suivante:
| Conduire sur la gauche | Conduisez sur le droit | |
|---|---|---|
| Conduire sur la gauche | 100, 100 | 0, 0 |
| Conduisez sur le droit | 0, 0 | 100, 100 |
Dans ce cas il ya deux ??quilibres de Nash de strat??gie pure, lorsque les deux choisir de conduire sur la gauche ou sur la droite. Si nous admettons strat??gies mixtes (o?? une strat??gie pure est choisi au hasard, sous r??serve de certaine probabilit?? fixe), puis il ya trois ??quilibres de Nash pour le m??me cas: deux nous avons vu de la forme pure strat??gie, o?? les probabilit??s sont (0%, 100 %) pour le joueur un, (0%, 100%) pour deux joueurs; et (100%, 0%) pour une joueur, (100%, 0%) respectivement pour deux joueurs. Nous ajoutons une autre o?? les probabilit??s pour chaque joueur est (50%, 50%).
Dilemme du prisonnier
(Mais attention aux diff??rences dans l'orientation de la matrice de gain)
Le dilemme du prisonnier a la m??me matrice de paiement comme repr??sent?? pour le jeu de coordination, mais maintenant C> A> D> B. Parce que C> A et D> B, chaque joueur am??liore sa situation en passant de la strat??gie n ?? 1 ?? la strat??gie n ?? 2, peu importe ce que l'autre joueur d??cide. Le dilemme du prisonnier a ainsi un seul ??quilibre de Nash: les deux joueurs choisissent la strat??gie n ?? 2 ("trahir"). Ce qui a longtemps fait de ce un cas int??ressant ?? ??tudier est le fait que D <A ("trahissent la fois") est globalement inf??rieur ?? "deux restent fid??les". La strat??gie optimale ?? l'??chelle mondiale est instable; ce ne est pas un ??quilibre.
Comme Ian Stewart a dit, "parfois des d??cisions rationnelles ne sont pas sensibles!".
??quilibres de Nash dans une matrice de paiement
Il ya une mani??re num??rique facile d'identifier des ??quilibres de Nash sur une matrice Payoff. Il est particuli??rement utile dans les deux jeux de personne o?? les joueurs ont plus de deux strat??gies. Dans ce cas, l'analyse formelle peut devenir trop longtemps. Cette r??gle ne se applique pas au cas o?? (stochastiques) strat??gies mixtes sont d'int??r??t. La r??gle est la suivante: si le premier num??ro de gain, dans le doublet de la cellule, est le maximum de la colonne de la cellule et si le second nombre est le maximum de la ligne de la cellule - alors la cellule repr??sente un ??quilibre de Nash .
Nous pouvons appliquer cette r??gle ?? une matrice 3x3:
| Option A | Option B | Option C | |
|---|---|---|---|
| Option A | 0, 0 | 25, 40 | 5, 10 |
| Option B | 40, 25 | 0, 0 | 5, 15 |
| Option C | 10, 5 | 15, 5 | 10, 10 |
En utilisant la r??gle, nous pouvons tr??s rapidement (beaucoup plus rapide que l'analyse formelle) voir que les cellules sont Equlibria Nash (B, A), (a, b) et (C, C). En effet, pour les cellules (B, A) 40 est le maximum de la premi??re colonne et 25 est le maximum de la deuxi??me rang??e. Pour (A, B) 25 est le maximum de la deuxi??me colonne et 40 est le maximum de la premi??re rang??e. Idem pour la cellule (C, C). Pour les autres cellules, l'un ou les deux ??l??ments ne sont pas Duplet le maximum des lignes et des colonnes correspondantes.
Cela dit, la m??canique m??me de trouver des cellules d'??quilibre est ??vidente: trouver le maximum d'une colonne et v??rifier si le second membre de la paire est le maximum de la rang??e. Si ces conditions sont remplies, la cellule repr??sente un ??quilibre de Nash. Consultez toutes les colonnes de cette fa??on de trouver toutes les cellules de NE. Une matrice NxN peut avoir entre 0 et NxN strat??gie pure ??quilibres de Nash.
Stabilit??
Le concept de stabilit??, utile dans l'analyse de nombreux types de ??quilibre, peut ??galement ??tre appliqu??e ?? des ??quilibres Nash.
Un ??quilibre de Nash pour un jeu de strat??gie mixte est stable si une faible variation (en particulier, une variation infinit??simale) dans les probabilit??s pour un joueur conduit ?? une situation o?? deux conditions sont r??unies:
- le joueur qui n'a pas chang?? a pas de meilleure strat??gie dans la nouvelle circonstance
- le joueur qui a fait le changement est maintenant jouer avec une strat??gie strictement pire
Si ces cas sont ?? la fois remplies, un joueur avec le petit changement dans sa strat??gie mixte reviendra imm??diatement ?? l'??quilibre de Nash. L'??quilibre est dite stable. Si la condition on ne tient pas alors l'??quilibre est instable. Si une seule condition d??tient alors il ya probablement un nombre infini de strat??gies optimales pour le joueur qui a chang??. John Nash a montr?? que cette derni??re situation ne pouvait pas se produire dans une gamme de jeux bien d??finies.
Dans l'exemple "de jeu de conduite" ci-dessus il ya deux ??quilibres stables et instables. Les ??quilibres impliquant mixtes strat??gies avec 100% probabilit??s sont stables. Si un joueur change l??g??rement ses probabilit??s, ils seront ?? la fois dans une situation d??savantageuse, et son adversaire ne auront aucune raison de modifier sa strat??gie ?? son tour. La (50%, 50%) ??quilibre est instable. Si un joueur change ses probabilit??s, puis l'autre joueur a imm??diatement une meilleure strat??gie soit au (0%, 100%) ou (100%, 0%).
La stabilit?? est cruciale dans les applications pratiques des ??quilibres de Nash, depuis la strat??gie mixte de chaque joueur ne est pas parfaitement connu, mais doit ??tre d??duite de distribution statistique de ses actions dans le jeu. Dans ce cas ??quilibres instables sont tr??s peu probables dans la pratique, car tout changement de minute dans les proportions de chaque strat??gie vu conduira ?? un changement de strat??gie et la rupture de l'??quilibre.
Notez que la stabilit?? de l'??quilibre est li??e ??, mais distincte de la stabilit?? d'une strat??gie.
Une Coalition-Proof ??quilibre de Nash (CPNE) (semblable ?? un solide ??quilibre de Nash) se produit lorsque les joueurs ne peuvent pas faire mieux, m??me se ils sont autoris??s ?? communiquer et collaborer avant le match. Chaque strat??gie corr??lation soutenue par r??it??r?? domination stricte et sur le Pareto fronti??re est un CPNE. En outre, il est possible pour un jeu d'avoir un ??quilibre de Nash capable de r??sister aux coalitions moins d'une taille sp??cifi??e, k. CPNE est li??e ?? la th??orie du noyau.
Occurrence
Si un jeu a un ??quilibre de Nash unique et est jou?? entre les acteurs, sous certaines conditions, alors l'ensemble de la strat??gie de NE seront adopt??es. Des conditions suffisantes pour garantir que l'??quilibre de Nash est jou?? sont:
- Les joueurs seront tous faire tout leur possible pour maximiser leur gain esp??r?? comme d??crit par le jeu.
- Les joueurs sont dans l'ex??cution sans faille.
- Les joueurs ont une intelligence suffisante pour en d??duire la solution.
- Il est de notori??t?? publique que tous les joueurs remplissent ces conditions, y compris celui-ci. Ainsi, non seulement chaque joueur doit conna??tre les autres joueurs remplissent les conditions, mais aussi ils doivent savoir que tous savent qu'ils les rencontrent, et nous savons qu'ils savent qu'ils savent qu'ils les rencontrent, et ainsi de suite.
Lorsque les conditions ne sont pas remplies
Exemples de probl??mes de la th??orie des jeux dans lesquels ces conditions ne sont pas remplies:
- La premi??re condition ne est pas remplie si le jeu ne d??crit pas correctement les quantit??s un joueur souhaite maximiser. Dans ce cas, il n'y a pas de raison particuli??re pour ce joueur ?? adopter une strat??gie d'??quilibre. Par exemple, le dilemme du prisonnier ne est pas un dilemme Si un joueur est heureux d'??tre emprisonn??s ind??finiment.
- Imperfection intentionnelle ou accidentelle dans l'ex??cution. Par exemple, un ordinateur capable de jouer logique sans d??faut faisant face ?? un second ordinateur sans d??faut entra??ne l'??quilibre. Introduction d'imperfection conduire ?? sa rupture, soit par perte pour le joueur qui commet l'erreur, ou par la n??gation de la 4e crit??re ??connaissance commune?? conduisant ?? la victoire possible pour le joueur. (Un exemple serait un joueur mettant soudainement la voiture en marche arri??re dans le jeu de ??poulet??, assurant un ni perte sc??nario sans victoire). Un exemple notable de cette situation dans la fiction est la s??rie Doctor Who Destiny of the Daleks
- Dans de nombreux cas, la troisi??me condition ne est pas remplie car, m??me si l'??quilibre doit exister, il ne est pas connu ?? cause de la complexit?? du jeu, par exemple dans ??checs chinois. Ou, se il est connu, il peut ne pas ??tre connu de tous les joueurs, comme lors de la lecture tic-tac-toe avec un petit enfant qui veut d??sesp??r??ment gagner (les autres crit??res).
- Le quatri??me crit??re de la connaissance commune ne peut pas ??tre respect??e, m??me si tous les joueurs ne, en fait, r??pondent ?? tous les autres crit??res. Joueurs m??fiant tort la rationalit?? de l'autre peut adopter des contre-strat??gies pour attendre jeu irrationnelle pour le compte de leurs adversaires. Ce est un facteur important dans " Poulet "ou un course aux armements, par exemple.
Lorsque les conditions sont remplies
En raison des conditions limit??es dans lesquelles NE peut effectivement ??tre observ??, ils sont rarement trait??s comme un guide pour le comportement au jour le jour, ou observ??es dans la pratique dans les n??gociations humains. Cependant, comme un concept th??orique dans l'??conomie et la biologie ??volutive du NE a pouvoir explicatif. Le gain en ??conomie est de l'argent, et dans la transmission de g??nes de la biologie ??volutive, les deux sont la ligne de fond fondamentale de la survie. Les chercheurs qui se appliquent la th??orie des jeux dans ces domaines que les agents affirment ne pas maximiser ces pour une raison quelconque seront en concurrence sur le march?? ou de l'environnement, qui sont attribu?? la possibilit?? de tester toutes les strat??gies. Cette conclusion est tir??e de la " stabilit?? th??orie "ci-dessus. Dans ces situations, l'hypoth??se que la strat??gie observ?? est en fait un NE a souvent ??t?? confirm??e par la recherche.
Preuve de l'existence
Comme ci-dessus, laissez-  un profil de strat??gie mixte de tous les joueurs, sauf pour le joueur
un profil de strat??gie mixte de tous les joueurs, sauf pour le joueur  . Nous pouvons d??finir une meilleure r??ponse la correspondance pour le joueur
. Nous pouvons d??finir une meilleure r??ponse la correspondance pour le joueur  ,
, 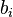 .
. 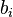 est une relation de l'ensemble de toutes les distributions de probabilit??s sur les profils de joueurs adversaire ?? un ensemble de lecteur
est une relation de l'ensemble de toutes les distributions de probabilit??s sur les profils de joueurs adversaire ?? un ensemble de lecteur  'de strat??gies, de telle sorte que chaque ??l??ment de
'de strat??gies, de telle sorte que chaque ??l??ment de
est une meilleure r??ponse ??  . D??finir
. D??finir
 .
.
On peut utiliser le Kakutani th??or??me du point fixe de prouver que 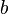 a un point fixe. Autrement dit, il se agit d'un
a un point fixe. Autrement dit, il se agit d'un 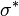 tel que
tel que 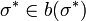 . Depuis
. Depuis 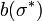 repr??sente la meilleure r??ponse pour tous les joueurs ??
repr??sente la meilleure r??ponse pour tous les joueurs ?? 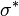 , L'existence du point fixe prouve qu'il ya un certain ensemble de la strat??gie qui est une meilleure r??ponse ?? lui-m??me. Aucun joueur ne peut faire mieux en se ??cartant, et il est donc un ??quilibre de Nash.
, L'existence du point fixe prouve qu'il ya un certain ensemble de la strat??gie qui est une meilleure r??ponse ?? lui-m??me. Aucun joueur ne peut faire mieux en se ??cartant, et il est donc un ??quilibre de Nash.
Lorsque Nash a fait ce point ?? John von Neumann en 1949, von Neumann c??l??bre rejet?? par les mots: ??Ce est trivial, vous savez. Ce est juste un th??or??me du point fixe." (Voir Nasar, 1998, p. 94.)