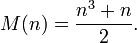Carr?? magique
Renseignements g??n??raux
Enfants SOS ont produit une s??lection d'articles de wikipedia pour les ??coles depuis 2005. Avez-vous voulez savoir sur le parrainage? Voir www.sponsorachild.org.uk
En math??matiques r??cr??atives, un carr?? magique d'ordre n est un arrangement de n de num??ros, habituellement distincts entiers , dans un carr?? , telles que les num??ros de n dans toutes les lignes, toutes les colonnes, et les deux diagonales r??sument ?? la m??me constante. Un carr?? magique normal contient les entiers de 1 ?? n ??. Le terme ??carr?? magique?? est aussi parfois utilis?? pour d??signer l'un des diff??rents types de mot carr??.
Carr??s magiques normales existent pour tous les ordres n ≥ 1, sauf n = 2, bien que le cas n = 1 est trivial-il se compose d'une seule cellule contenant le num??ro 1. Le plus petit de cas non n??gligeable, illustr?? ci-dessous, est d'ordre 3.

La somme constante dans chaque ligne, colonne et diagonale est appel??e constante magique ou somme magique, M. La constante magique d'un carr?? magique normale ne d??pend que de n et a la valeur
Pour carr??s magiques normales d'ordre n = 3, 4, 5, ..., les constantes magiques sont:
- 15, 34, 65, 111, 175, 260, ... (s??quence A006003 dans OEIS ).
Histoire de carr??s magiques
Le carr?? Lo Shu (3 x 3 carr?? magique)
Litt??rature chinoise datant de d??s 650 BC raconte la l??gende de Lo Shu ou ??d??filement de la rivi??re Lo". Dans la Chine antique , il y avait une ??norme inondation. Les gens ont essay?? d'offrir un sacrifice au dieu de la rivi??re de l'une des rivi??res en crue, la rivi??re Lo, pour calmer sa col??re. Puis, il a ??merg?? de l'eau une tortue avec un chiffre / motif curieux sur sa coquille; il y avait des points circulaires de chiffres qui ont ??t?? dispos??s en trois par trois mod??le neuf grille de sorte que la somme des nombres dans chaque ligne, colonne et diagonale ??tait le m??me: 15. Ce nombre est ??gal au nombre de jours dans chaque des 24 cycles de la Ann??e solaire chinoise. Ce mod??le, d'une certaine mani??re, a ??t?? utilis?? par le peuple dans le contr??le de la rivi??re.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Le Lo Shu Square, le carr?? magique sur la carapace de tortue est appel??, est le carr?? magique normale unique de l'ordre de trois dans laquelle 1 est ?? la base et 2 est dans le coin sup??rieur droit. Chaque carr?? magique normale d'ordre trois est obtenu ?? partir du Lo Shu par rotation ou r??flexion.
La Place de Lo Shu est aussi appel?? le carr?? magique de Saturne ou Cronos. Sa valeur num??rique est obtenu ?? partir du fonctionnement du I Ching lorsque le Trigrammes sont plac??s dans un ordre donn?? dans la premi??re carte de la rivi??re, le Ho Tu ou fleuve Jaune . Le Ho Tu produit 4 carr??s de Hexagrammes 8 x 8 dans ses valeurs ext??rieures de 1-6, 2-7, 3-8 et 4-9, et ces places ext??rieures peuvent ensuite ??tre ajout??es sym??triquement ensemble pour donner une place centrale int??rieure de 5 ?? 10. Les valeurs centrales du Ho Tu sont celles de l'Lo Shu (afin qu'ils travaillent ensemble), puisque dans la valeur totale de 15 x 2 (clair et fonc??) se trouve le nombre d'ann??es dans le cycle de pr??cession des ??quinoxes (12 960 x 2 = 25 920). Le Ho Tu produit un total de 40 lumi??re et 40 chiffres noirs appel?? les jours et les nuits (les alternances de lumi??re et l'obscurit??), et un total de 8 x 8 x 8 hexagrammes dont plus sym??trique oppos??e ??gale 8640, donc chaque valeur d'un carr?? est appel?? une saison comme elle est ??gale ?? 2160. 8640 est le nombre d'heures dans une ann??e de 360 jours et 2160 ann??es ??quivaut ?? une Aeon (12 ??ons = 25 920 ans).
Pour valider les valeurs contenues dans les deux cartes hydrographiques (Ho Tu et Lo Shu) du I Ching fournit des num??ros de Ciel et la Terre qui sont les 'origine trigrammes ??(p??re et m??re) de 1 ?? 10. ciel ou d'un trigramme avec tout ininterrompue lignes (lignes de lumi??re - yang) re??oivent des num??ros impairs 1,3,5,7,9, et la Terre un trigramme avec toutes les lignes bris??es ont m??me nombre 2,4,6,8,10. Si chacune des lignes de trigramme est donn??e une valeur en multipliant le nombre de Ciel et la Terre, alors la valeur de chaque ligne dans le ciel une serait 1 + 2 + 3 = 6, et son partenaire dans le Ho Tu de Terre 6 serait 6 + 12 + 18 = 36, ces deux 'origine trigrammes' produire ainsi 6 trigrammes plus (ou des enfants dans toutes leurs combinaisons) - et lorsque les s??quences de trigrammes sont plac??s perpendiculairement ?? l'autre, ils produisent un carr?? de 8 x 8 des hexagrammes (ou cubes) qui ont chacun six lignes de valeurs. De ce simple point la structure complexe des math??matiques ??volue comme une progression hexad??cimal, et ce est l'hexagone qui est le lien de la carapace de tortue ou tortue. Dans les textes chinois du I Ching la lune est symbolique de l'eau (obscurit??) dont les transformations ou des changements de cr??er la lumi??re ou de feu - la valeur sombre 6 cr??e la lumi??re lorsque son num??ro est augment?? de 1. Ce m??me principe peut ??tre trouv?? dans les calendriers antiques comme le ??gyptienne, comme l'ann??e de 360 jours de 8640 heures a ??t?? divis?? par 72 pour produire les 5 jours ou 120 heures suppl??mentaires sur lesquelles les dieux sont n??s. Il faut 72 ann??es pour les cieux de se d??placer 1 degr?? ?? travers son pr??cession.
L'importance culturelle des carr??s magiques
Les carr??s magiques ont fascin?? l'humanit?? ?? travers les ??ges, et ont ??t?? autour depuis plus de 4000 ans. Ils se trouvent dans un certain nombre de cultures, y compris l'Egypte et l'Inde, grav?? sur la pierre ou de m??tal et port?? comme talismans, la conviction ??tant que les carr??s magiques avaient astrologiques qualit??s et divinatoires, leur utilisation assurant la long??vit?? et la pr??vention des maladies.
Le Kubera-Kolam est une peinture de plancher utilis??e en Inde, qui est sous la forme d'un carr?? magique d'ordre trois. Ce est essentiellement le m??me que le carr?? Lo Shu, mais avec 19 ajout?? ?? chaque num??ro, ce qui donne une constante de 72 magique.
| 23 | 28 | 21 |
| 22 | 24 | 26 |
| 27 | 20 | 25 |
Saoudite
Les carr??s magiques ??taient connus Math??maticiens arabes, peut-??tre d??s le 7??me si??cle, lorsque les Arabes obtenu en contact avec la culture indienne ou sud-asiatique, et ont appris les math??matiques et l'astronomie indiennes, y compris d'autres aspects de math??matiques combinatoires . Il a ??galement ??t?? sugg??r?? que l'id??e est venue par la Chine. Les premiers carr??s magiques d'ordre 5 et 6 apparaissent dans une encyclop??die de Bagdad vers 983 AD, le Rasa'il Ihkwan al-Safa (l'Encyclop??die de la Brethern de la Puret??); simples carr??s magiques ont ??t?? connus ?? plusieurs math??maticiens arabes ant??rieures.
Le math??maticien arabe Ahmad al-Buni, qui a travaill?? sur les carr??s magiques autour de 1200 AD, lui attribue des propri??t??s mystiques pour eux, m??me si aucun d??tail de ces propri??t??s suppos??es sont connus. Il ya aussi des r??f??rences ?? l'utilisation des carr??s magiques dans les calculs astrologiques, une pratique qui semble avoir son origine avec les Arabes.
Inde
Un carr?? magique d??but bien connu en Inde se trouve dans Khajuraho dans le Parshvanath Temple Jain. Elle date du 10??me si??cle.
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Ce est appel?? le Chautisa Yantra, puisque chaque sous-carr?? sommes ?? 34.
Europe
En 1300, se appuyant sur le travail de l'arabe Al-Buni, savant grec byzantin Manuel Moschopoulos a ??crit un trait?? de math??matiques sur le sujet des carr??s magiques, en laissant de c??t?? le mysticisme de ses pr??d??cesseurs. Moschopoulos est pens?? pour ??tre le premier occidental ?? avoir ??crit sur le sujet. Dans les ann??es 1450 l'italienne Luca Pacioli ??tudi?? carr??s magiques et recueilli un grand nombre d'exemples.
Dans environ 1510 Heinrich Cornelius Agrippa ??crit De occulta Philosophia, se appuyant sur les Herm??tique et magie des ??uvres Marsile Ficin et Pic de la Mirandole, et en elle il exposa sur les vertus magiques de sept carr??s magiques de commandes 3-9, chacun associ?? ?? l'une des astrologiques plan??tes. Ce livre a ??t?? tr??s influent dans toute l'Europe jusqu'?? ce que le Contre-R??forme, et les carr??s magiques d'Agrippa, parfois appel?? Kameas , continuent ?? ??tre utilis??s dans la magie c??r??monielle moderne de la m??me mani??re que il a d'abord prescrit.
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

L'utilisation la plus courante pour ces Kameas est de fournir un motif sur laquelle pour construire la sceaux de spiritueux, anges ou d??mons; les lettres du nom de l'entit?? sont convertis en num??ros, et les lignes sont trac??es ?? travers le motif que ces chiffres successifs font sur le kamea. Dans un contexte magique, le carr?? magique terme se applique aussi ?? une vari??t?? de mot carr??s ou le nombre carr??s trouv?? dans la magie grimoires, y compris certains qui ne suivent pas de tendance ??vidente, et m??me ceux avec des num??ros diff??rents de lignes et de colonnes. Ils sont g??n??ralement destin??s ?? ??tre utilis??s comme des talismans. Par exemple, les carr??s suivants sont: La Carr?? Sator, l'une des places les plus c??l??bres magiques trouv??s dans un certain nombre de grimoires y compris le Cl?? de Salomon; un carr?? "?? surmonter l'envie", du Livre de puissance; et deux places de Le Livre de la Magie Sacr??e des Abramelin le Mage, le premier ?? provoquer l'illusion d'un superbe palais ?? appara??tre, et la seconde ?? ??tre port?? sur la t??te d'un enfant au cours d'une ang??lique invocation:
|
|
|
|
Carr?? magique de Albrecht D??rer

La place pour quatre-magie La gravure de Albrecht D??rer Melencolia I est consid??r?? comme le premier vu dans l'art europ??en. Il est tr??s similaire ?? La place de Yang Hui, qui a ??t?? cr???? en Chine environ 250 ans avant l'??poque de D??rer. La somme 34 peut ??tre trouv??e dans les lignes, colonnes, diagonales, chacun des quadrants, le centre quatre places, les places d'angle, les quatre num??ros externes dans le sens horaire ?? partir des coins (3 + 8 + 14 + 9) et de m??me les quatre contre- -clockwise (les emplacements des quatre reines dans les deux solutions de la 4 reines de puzzle ), Les deux ensembles de quatre chiffres sym??triques (2 + 8 + 9 + 15 3 + 5 et + 12 + 14) et la somme des deux entr??es milieu des deux colonnes ext??rieures et de lignes (par exemple, 5 + 9 + 8 + 12 ), ainsi que plusieurs quatuors en forme de cerf-volant, par exemple 3 + 5 + 11 + 15; les deux num??ros dans le milieu de la rang??e du bas donnent la date de la gravure: 1514. La M??lancolie de D??rer, je joue un r??le cl?? dans Le Voleur d'art, un roman de Noah Charney (Atria, 2007).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Le carr?? magique Sagrada Fam??lia

La fa??ade de la Passion du Sagrada Familia ?? Barcelone , con??u par le sculpteur Josep Subirachs, dispose d'un carr?? de 4 ?? 4 de la magie:
La constante magique de la place est de 33, l'??ge de J??sus au moment de la Passion. Structurellement, il est tr??s similaire ?? le carr?? magique Melancholia, mais il a eu les num??ros dans quatre des cellules r??duites par une.
| 1 | 14 | 14 | 4 |
| 11 | 7 | 6 | 9 |
| 8 | 10 | 10 | 5 |
| 13 | 2 | 3 | 15 |
Tout en ayant le m??me sch??ma de sommation, ce ne est pas un carr?? magique normale comme ci-dessus, que deux num??ros (10 et 14) sont dupliqu??s et deux (12 et 16) sont absents, ?? d??faut de la r??gle 1 → n??.
Types de carr??s magiques et leur construction
Il ya plusieurs fa??ons de construire des carr??s magiques, mais la norme (et la plus simple) est de suivre certaines configurations / formules qui g??n??rent des motifs r??guliers. Les carr??s magiques existent pour toutes les valeurs de n, ?? une exception pr??s - il est impossible de construire un carr?? magique d'ordre 2. Les carr??s magiques peuvent ??tre class??s en trois types: bizarre, doublement m??me (n divisible par quatre) et individuellement, m??me (n m??me, mais pas divisible par quatre). Places impaires et doublement m??me magiques sont faciles ?? g??n??rer; la construction de Singly m??me carr??s magiques est plus difficile, mais il existe plusieurs m??thodes, y compris la LUX m??thode pour carr??s magiques (en raison de John Horton Conway) et le Strachey m??thode pour les carr??s magiques.
La th??orie des groupes a ??galement ??t?? utilis?? pour la construction de nouveaux carr??s magiques d'un ordre donn?? ?? partir de l'un d'eux, se il vous pla??t voir .
| Combien de n ?? n carr??s magiques pour n> 5? |
Le nombre de places diff??rentes n ?? n magiques pour n 1-5, sans compter les rotations et r??flexions:
- 1, 0, 1, 880, 275 305 224 (s??quence A006052 dans OEIS ).
Le nombre pour n = 6 a ??t?? estim??e ?? 1,7745 ?? 10 19.
Une m??thode pour construire un carr?? magique d'ordre impair
A partir de la colonne centrale de la premi??re rang??e avec le num??ro 1, le mouvement de fond pour remplir les carr??s est en diagonale et ?? droite, une ??tape ?? la fois. Si un carr?? plein est rencontr??, on se d??place verticalement vers le bas d'une case ?? la place, puis en continuant comme avant. Quand un mouvement laisserait la place, il est enroul?? autour de la derni??re ligne ou la premi??re colonne, respectivement.
Des tendances similaires peuvent ??galement ??tre obtenus en partant d'autres carr??s.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Les formules suivantes permettent de construire des carr??s magiques d'ordre impair
| ||||||||||||
* Racines carr??es sont plus faciles ?? calculer que les racines cubes
Exemple:
| ||||||||||||
Le "Nombre Moyen" est toujours dans le fond en diagonale gauche vers le haut ?? droite.
Le "dernier num??ro" est toujours oppos??e ?? la num??ro 1 dans une colonne ou une ligne ext??rieure.
Un proc??d?? de construction d'un carr?? magique d'ordre doublement m??me
Doublement m??me signifie que n est ??gal ?? un multiple pair d'un entier pair; ou 4p, o?? p est un nombre entier. par exemple 4, 8, 12
Mod??le g??n??rique
Tous les num??ros sont ??crits dans l'ordre de droite ?? gauche sur chaque ligne ?? son tour, ?? partir du coin sup??rieur gauche. Les chiffres sont ensuite soit conserv??es dans le m??me lieu ou ??chang??s avec leurs num??ros diam??tralement oppos??s dans un certain sch??ma r??gulier. Dans le carr?? magique d'ordre quatre, les chiffres dans les quatre places centrales et un carr?? ?? chaque coin sont conserv??s au m??me endroit et les autres sont ??chang??es avec leurs num??ros diam??tralement oppos??s.
Une construction d'un carr?? magique d'ordre 4
Allez ?? gauche ?? droite sur la place de remplissage de comptage et en remplissant uniquement sur les diagonales. Puis continuer en va de gauche ?? droite ?? partir du haut ?? gauche de la table et de remplir le compte ?? rebours ?? partir de 16 ou n??. Comme indiqu?? ci-dessous.
|
| ||||||||||||||||||||||||||||||||||||||||
Le medjig-m??thode de construction carr??s magiques d'ordre pair n> 4
Cette m??thode ludique est bas?? sur un jeu math??matique de 2006 publi??e appel?? medjig (auteur: Willem Barink, r??dacteur en chef: Philos-Spiele). Les pi??ces du puzzle sont medjig carr??s divis??s en quatre quadrants sur lesquels les num??ros 0, 1, 2 et 3 sont parsem??es dans toutes les s??quences. Il ya 18 places, chaque s??quence se produit trois fois. Le but du jeu est de prendre neuf carr??s de la collection et les disposer dans un 3 x 3 "medjig-carr??" de mani??re ?? ce que les s??ries, colonnes et diagonales form??es par les quadrants, montrent la somme de neuf.
La fa??on medjig de construction d'un carr?? magique d'ordre 6 va comme suit. Organiser un carr?? de 3 x 3 medjig (pour plus de commodit?? cette fois vous pouvez choisir illimit??e de l'ensemble de la collection). Ensuite, prendre le classique carr?? magique 3 x 3 bien connu et diviser tous les domaines de l'informatique dans quatre quadrants. Ensuite remplissez ces quadrants avec le nombre original et ses trois modulo-neuf num??ros jusqu'?? 36, suivant le mod??le de la medjig-solution. Ce faisant, le champ d'origine avec le num??ro 8 donne les quatre sous-champs avec les num??ros 8 (= 8 + 0x9), 17 (= 8 + 1x9), 26 (= 8 + 2x9) et 35 (= 3x9 + 8), le champ avec le num??ro 3 donne les num??ros 3, 12, 21 et 30, etc ... Voir l'illustration ci-dessous.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De la m??me fa??on, vous pouvez construire un carr?? magique d'ordre 8. Vous devez d'abord construire une solution de medjig 4 x 4 (somme de toutes les s??ries, colonnes et diagonales 12). Et puis agrandir par exemple le bien-connu D??rer 4 x 4 carr?? magique modulo-16 ?? 64. Pour la construction d'un carr?? magique d'ordre 10 vous avez d'organiser une solution de 5 x 5 medjig, pour lequel deux ensembles de pi??ces sont n??cessaires medjig . Pour l'ordre 12 vous pouvez simplement dupliquer horizontalement et verticalement une solution 3 x 3 medjig puis agrandir modulo-36-144 du carr?? magique pour 6 faite ci-dessus. Afin 16 va de la m??me mani??re.
La construction de carr??s panmagique
Ne importe quel nombre p dans l'ordre n-carr?? peut ??tre ??crit de mani??re unique sous la forme d'un p = + r, avec r choisi parmi {1, ..., n}. Veuillez noter qu'en raison de cette restriction, A et R sont pas le quotient et le reste de la division par n p habituel. Par cons??quent, le probl??me de la construction peut ??tre divis?? en deux probl??mes plus faciles ?? r??soudre. Ainsi, la construction de deux correspondant grilles carr??es d'ordre n panmagique satisfaisante propri??t??s, un pour les a-chiffres (0, ...., N-1), et un pour les r-num??ros (1, ...., N). Cela n??cessite beaucoup de d??routant, mais peut ??tre fait. En cas de succ??s, les combiner en une - panmagique - carr??. Van den Essen et bien d'autres cens??s ce ??tait aussi la fa??on dont le grand Benjamin Franklin (1706-1790) construit ses c??l??bres places Franklin. Trois carr??s panmagique sont pr??sent??s ci-dessous. Les deux premi??res places ont ??t?? construits Avril 2007 par Barink, le troisi??me est quelques ann??es plus ??g??, et provient de Donald Morris, qui a utilis??, comme il le suppose, la fa??on franklin de construction.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L'ordre 8 carr??s satisfait toutes les propri??t??s panmagique, y compris ceux de Franklin. Il se compose de quatre unit??s de 4x4 parfaitement panmagique. Notez que les deux afin douze carr??s montrent la propri??t?? que toute ligne ou une colonne peuvent ??tre divis??s en trois parties ayant une somme de 290 (= 1/3 de la somme totale d'une ligne ou colonne). Cette propri??t?? compense l'absence de la propri??t?? plus standard franklin panmagique que toute moiti?? ligne ou une colonne montre la somme de moiti?? du total. Pour le reste de l'ordre de 12 places diff??rent un carr?? lot.The Barink 12x12 est compos?? de neuf unit??s de 4x4 parfaitement panmagique, en outre des quatre num??ros cons??cutifs ?? partir sur un dr??le d'endroit dans une ligne ou une colonne montrer une somme de 290. Le carr?? de 12x12 Morris manque ces propri??t??s, mais au contraire montre franklindiagonals constants. Pour une meilleure compr??hension de la CONSTRUIRE d??composer les carr??s comme d??crit ci-dessus, et voyez comment cela a ??t?? fait. Et noter la diff??rence entre les constructions Barink d'une part, et la construction Morris / Franklin d'autre part.
Dans les math??matiques livre dans la Time-Life Science Library Series, carr??s magiques par Euler et Franklin sont pr??sent??s. Franklin con??u celui-ci afin que tout sous-ensemble de quatre carr??s (des quatre carr??s contigus qui forment un carr?? plus grand, ou tout quatre carr??s ??quidistants du centre) au total 130. Dans la place d'Euler, les lignes et les colonnes chaque total 260, et ?? mi-chemin, ils se ??l??vent ?? 130 - et un jeu d'??checs chevalier, rendant ses mouvements en forme de L sur la place, peut toucher tous les 64 cases dans l'ordre num??rique.
La construction d'un carr?? magique en utilisant des algorithmes g??n??tiques
Un carr?? magique peut ??tre construit en utilisant algorithmes g??n??tiques. Ce est un processus d'essais et d'erreurs ??l??gante dans laquelle une population initiale de carr??s magiques avec des valeurs al??atoires sont g??n??r??s. Les fitnesses de ces carr?? magique individuelle sont calcul??s sur la base du ??platitude?? du carr?? magique, ce est le degr?? d'??cart dans les sommes des lignes, des colonnes et des diagonales. La population de carr??s magiques se croiser (valeurs d'??change) de mani??re coh??rente ?? la g??n??tique, bas??e sur le score de remise en forme des carr??s magiques. Ainsi, les carr??s magiques avec un score de fitness sup??rieur auront une probabilit?? plus ??lev??e de reproduction. Dans le processus de croisement o?? les carr??s magiques ??changent leurs valeurs, un facteur de mutation est introduite, en imitant une mutation g??n??tique dans la nature. Cette mutation sera inclus ou exclu naturellement de la solution en fonction de leur contribution ?? la remise en forme du carr?? magique. La prochaine g??n??ration de la population carr?? magique est ?? nouveau calcul??e pour leur condition physique, et ce processus se poursuit jusqu'?? ce qu'une solution a ??t?? trouv??e.
G??n??ralisations
Contraintes suppl??mentaires
Certaines restrictions suppl??mentaires peuvent ??tre impos??es sur les carr??s magiques. Si non seulement les diagonales principales mais aussi les diagonales bris??es somme soit ??gale ?? la constante magique, le r??sultat est un panmagique carr??. Si ??lever chaque num??ro ?? certains pouvoirs donne un autre carr?? magique, le r??sultat est un bimagique, un trimagique, ou, en g??n??ral, un multimagique carr??.
Diff??rentes contraintes
Parfois, les r??gles de carr??s magiques sont d??tendus, de sorte que seules les lignes et de colonnes, mais pas n??cessairement les diagonales r??sument ?? la constante magique. En heterosquares et antimagie carr??s, les 2 n + 2 sommes doivent tous ??tre diff??rents.
Autres op??rations
Au lieu d'ajouter les nombres dans chaque ligne, colonne et diagonale, on peut appliquer une autre op??ration. Par exemple, un carr?? magique multiplicatif a un produit constant de num??ros.
|
| ||||||||||||||||||||||||||||||||
Autres formes magiques
D'autres formes que peuvent ??tre consid??r??es comme des carr??s, r??sultant, par exemple, dans ??toiles magiques et hexagones magiques. En remontant dans les r??sultats de dimension dans cubes magiques, tesseracts magiques et autres hypercubes magiques.
Edward Shineman, une forme de renomm??e internationale constructiviste magie, a d??velopp?? encore une autre conception en forme de diamants magiques. Il a fait beaucoup de ces fins comm??moratives et historiques, et a ??galement exp??riment?? avec d'autres ?? double rectangle autonome / combinaisons carr??s, chiffres en forme de L "??claircissement", et plus encore. Les diamants ont ??t?? faites en l'honneur des ??v??nements et des personnes allant de Tiger Woods ?? Ronald Reagan, de l'Universit?? Cornell anniversaire de la anniversaires sp??ciaux pour les familles. Plusieurs de ses ??uvres ont ??t?? pr??sent??es dans les livres carr??s magiques, ainsi que de multiples publications dans Le Journal de math??matiques de loisirs. Un tableau de ses contributions magiques peut ??tre trouv?? ?? eds-magic-squares.com.
Extensions combin??es
On peut combiner deux ou plusieurs des extensions ci-dessus, r??sultant en des objets tels que des hypercubes multimagiques multiplicatifs. Peu semble ??tre connu sur ce sujet.
Probl??mes connexes
Au fil des ans, de nombreux math??maticiens, y compris Euler et Cayley ont travaill?? sur les carr??s magiques, et a d??couvert les relations fascinantes.
Carr?? magique des nombres premiers
Rudolf Ondrejka (1928-2001) d??couvrit le carr?? magique 3x3 suivante de nombres premiers , dans ce cas neuf Chen amorce:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
Le Green-Tao th??or??me implique qu'il n'y a arbitrairement grands carr??s magiques constitu??s de nombres premiers.
probl??me n-Queens
En 1992, Demir??rs, Rafraf et Tanik publi?? une m??thode pour convertir des carr??s magiques dans N-reines solutions, et vice versa.
Date de carr?? magique
Un carr?? date de magie est un carr?? de 4 ?? 4 de magique dans lequel les num??ros d'une date donn??e (par exemple, 15 avril 1707) sont utilis??s pour construire la premi??re ligne (4, 15, 17, 07). Le constante magique (M) d'un carr?? magique "normal" 4 ?? 4 est 34. Si les quatre num??ros dans un jour ne est pas ??gale ?? 34, nous ne pouvons pas construire un carr?? magique "normal" pour cette date. Dans l'exemple ci-dessus, m = 43:
| 4 | 15 | 17 | 07 |
| 5 | 19 | 13 | 6 |
| 20 | 9 | 2 | 12 |
| 14 | 0 | 11 | 18 |
La seule diff??rence entre un carr?? magique et un carr?? magique de ce jour est que, dans une date magique r??p??tition carr??e des nombres ne est pas autoris?? dans une ligne, sauf la premi??re, alors que dans un carr?? magique ??normal??, la r??p??tition ne est pas autoris?? dans une ligne .
Nombre / Word Magic Place
A Nombre / Parole carr?? combinaison magique est construit en utilisant les trois r??gles suivantes:
- Faire un carr?? magique normal de l'ordre 3 ?? l'aide des chiffres.
- Comptez le nombre de lettres dans chaque num??ro et de remplacer le num??ro de ce compte.
- La nouvelle place doit ??galement ??tre magique.
Un exemple d'un tel carr?? est indiqu?? ci-dessous:
|
|
| ||||||||||||||||||||||||||||||||||||
Probl??me Tarry-Escott
Par une ??trange co??ncidence, le carr?? 3 ?? 3 magique contient une solution ?? la Probl??me Tarry-Escott.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Pr??parer deux ensembles de nombres du carr?? magique ci-dessus en combinant les num??ros de derni??res lignes et derni??res colonnes dans les directions gauche et ?? droite:
- {492, 276, 618, 834}
- {294, 438, 816, 672}.
Tarry-Escott Solution:
- 492 1 276 + 1 618 + 1 834 + 1 = 294 1 + 438 1 + 816 1 + 672 1
- 492 2 + 276 2 + 618 2 + 834 2 = 294 2 + 438 2 + 816 2 + 672 2
- 3 492 + 3 276 + 3 618 + 834 = 294 3 + 3 438 3 + 3 816 + 3 672.
Carr??s magiques dans la litt??rature contemporaine
Dans le chapitre 2 de The Great cerveau est de retour John D. Fitzgerald, Tom, alias le ??Grand Brain", se souvient d'avoir ??t?? dit par un enseignant d'un carr?? magique. Apr??s y avoir travaill?? pendant trois jours, il arrive avec l'Ordre 3, Sum 15 carr??. Il ??tablit alors le ??jeu des nombres", arrondissant ses amis et d'expliquer le concept, de charge de 10 cents pour jouer avec un prix de 50 cents pour tous ceux qui peuvent le r??soudre dans les deux jours, distribuant une feuille avec la grille 3 * 3 et les num??ros un ?? neuf ?? chaque joueur, et en donnant la permission ?? tous les participants d'obtenir l'aide de leurs parents. Pensant que ce sera facile, tous les 20 enfants pr??sents, dont son fr??re John (le narrateur) choisir de jouer et de lui donner un sou. John montre ?? leur p??re, le seul dipl??m?? de l'universit?? de la ville. Son p??re explique que la premi??re chose ?? faire est de faire une liste de toutes les combinaisons de trois num??ros 1-9 qui totalisent 15, excluant ceux dans lesquels un num??ro est utilis?? plus d'une fois. Puis (montrant un manque d'expertise sur le sujet), il dit que vous devez ??continuer ?? essayer les diff??rentes combinaisons jusqu'?? ce que vous obtenez la bonne r??ponse." John fait la liste, et passe tout son temps libre, il a au cours des deux prochains jours en essayant de mettre les combinaisons ensemble, sans succ??s. Son p??re lui a dit de le faire par ??limination et de commencer avec les trois places du milieu, mais ne pr??cise pas. Apr??s deux jours, personne ne l'a r??solu, et certains pensent qu'il ne peut pas ??tre fait. Mais lorsque le d??lai passe et il n'y a pas de gagnants, Tom r??v??le la r??ponse.
En Le roman de Steve Martin Le plaisir de ma compagnie, le personnage principal Daniel Pecan Cambridge construit carr??s magiques comme un moyen de se d??tendre.