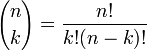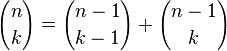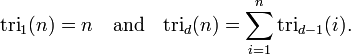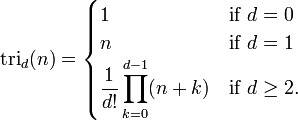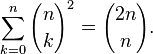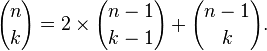Le triangle de Pascal

Saviez-vous ...

SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

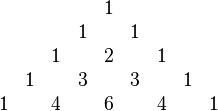
$\ Begin {matrix} &&&&& 1 \\ &&&& 1 && 1 \\ &&& 1 && && 2 1 1 \\ && && && 3 3 && 1 \\ & 1 && && 4 6 4 && && 1 \ end {matrix}$

Les cinq premi??res lignes du triangle de Pascal

En math??matiques , le triangle de Pascal est un arrangement g??om??trique des coefficients binomiaux dans un triangle . Il est nomm?? d'apr??s Blaise Pascal dans une grande partie du monde occidental, bien que d'autres math??maticiens ont ??tudi?? il si??cles avant lui dans l'Inde , la Perse , la Chine et l'Italie . Les lignes du triangle de Pascal sont classiquement ??num??r??s en commen??ant par la ligne z??ro, et les num??ros de lignes impaires sont g??n??ralement d??cal??s par rapport aux nombres de lignes paires. Une construction simple du triangle se d??roule de la mani??re suivante. Sur la ligne de z??ro, ne ??crire que le nombre 1. Ensuite, pour construire les ??l??ments de lignes suivantes, ajouter le num??ro directement au-dessus et ?? gauche avec le nombre directement au-dessus et ?? droite pour trouver la nouvelle valeur. Si le nombre ?? droite ou ?? gauche ne est pas pr??sente, le remplacer par un z??ro ?? sa place. Par exemple, le premier num??ro de la premi??re ligne est 0 + 1 = 1, tandis que les num??ros 1 et 3 de la troisi??me rang??e sont ajout??s pour produire le num??ro 4 dans la quatri??me rang??e.

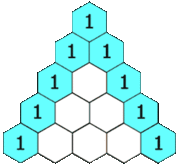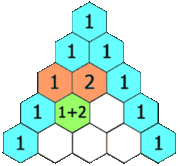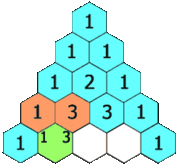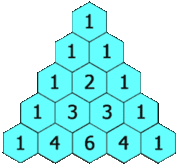
Chaque chiffre dans le triangle est la somme des deux directement au-dessus.

Cette construction est en relation avec des coefficients binomiaux par La r??gle de Pascal, qui stipule que si

${N \ choisir k} = \ frac {n!} {K! (N-k)!}$

est le ki??me coefficient binomial dans le d??veloppement du bin??me de (x + y) ^n, o?? n! est la factorielle de n, puis

${N \ choisir k} = {n-1 \ choisir k-1} + {n-1 \ choisir k}$

pour tout entier n positif ou nul et tout entier k compris entre 0 et n.

Le triangle de Pascal a ??lev?? g??n??ralisations dimensions. La version en trois dimensions est appel??e Pyramide de Pascal ou de t??tra??dre de Pascal, tandis que les versions g??n??raux sont appel??s Les simplexes de Pascal - Voir aussi pyramide , t??tra??dre , et simplex.

Le triangle

Voici rang??es de z??ro ?? seize du triangle de Pascal:

                                                 1
                                              1 1
                                           1 2 1
                                        1 3 3 1
                                     1 4 6 4 1
                                  1 5 10 10 5 1
                               1 6 15 20 15 6 1
                            1 7 21 35 35 21 7 1
                         1 8 28 56 70 56 28 8 1
                      1 9 36 84 126 126 84 36 9 1
                   1 10 45 120 210 252 210 120 45 10 1
                1 11 55 165 330 462 462 330 165 55 11 1
             1 12 66 220 495 792 924 792 495 220 66 12 1
          1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
       1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
    1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1

Triangle et binomiale les expansions de Pascal

Le triangle de Pascal d??termine les coefficients qui se posent dans expansions binomiale. Pour un exemple, envisager l'expansion

(X + y) = x ² + ² 2 + xy = y ² 1 x ² y 2 + ⁰ x ¹ y ¹ + y 1 x ^{2 0.}

Remarquez les coefficients sont les nombres dans la rang??e deux de Pascal triangle: 1, 2, 1. En g??n??ral, quand un binomiale comme x + y est ??lev?? ?? une puissance de nombre entier positif, nous avons:

(X + y) = a ⁿ x ⁿ ₀ + a ₁ x + y ^n-1 x ⁿ ₂ y ^{2 -2} + ... + a _n ^{n -1} _-1 xy + a _n y ^n,

o?? les coefficients a _i dans cette expansion sont pr??cis??ment les num??ros sur la ligne n du triangle de Pascal. Autrement dit,

$a_i = {n \ choisir i}.$

Ceci est le bin??me.

Notez que l'ensemble de la diagonale droite du triangle de Pascal correspond au coefficient de y ⁿ dans ces expansions binomiales, tandis que les prochaines diagonale correspond au coefficient de xy ^{n -1} et ainsi de suite.

Pour voir comment le bin??me se rapporte ?? la construction simple du triangle de Pascal, consid??rons le probl??me de calcul des coefficients de l'expansion de (x + 1) ^{n 1} en termes de coefficients correspondant de (x + 1) ⁿ (valeur Y = 1 pour simplifier). Supposons donc que

$(X + 1) ^ n = \ sum_ {i = 0} ^ n a_i x ^ i.$

Maintenant

$(X + 1) ^ {n + 1} = (x + 1) (x + 1) = x ^ n (x + 1) + n ^ (x + 1) n = ^ \ sum_ {i = 0} ^ n a_i x ^ {i + 1} + \ sum_ {i = 0} ^ n a_i x ^ i.$

Les deux sommations peuvent ??tre r??organis??es comme suit:

$\ Begin {align} et \ sum_ {i = 0} ^ {n} a_ {i} x ^ {i + 1} + \ sum_ {i = 0} ^ n a_i x ^ i \\ & {} = \ sum_ {i = 1} ^ {n + 1} a_ {i-1} x ^ {i} + \ sum_ {i = 0} ^ n a_i x ^ i \\ & {} = \ sum_ {i = 1} ^ {n} a_ {i-1} x ^ {i} + \ sum_ {i = 1} ^ n a_i x ^ i + a_0x ^ 0 + a_ {n} x ^ {n + 1} {} \\ & = \ sum_ {i = 1} ^ {n} (a_ {i-1} + a_i) x ^ {i} + a_0x ^ 0 + a_ {n} x ^ {n + 1} {} \\ & = \ sum_ {i = 1} ^ {n} (a_ {i-1} + a_i) x ^ {} i + x + x ^ 0 ^ {n + 1} \ end {align}$

(?? cause de la fa??on dont ??lever un polyn??me dans un r??seau d'alimentation, un ₀ = a _n = 1).

Nous avons maintenant une expression pour le polyn??me (x + 1) ^{n 1} en termes de coefficients de (x + 1) ⁿ (ce sont les a _i s), ce est ce que nous avons besoin si nous voulons exprimer une ligne dans termes de la ligne au-dessus. Rappelons que tous les termes d'une diagonale allant du coin sup??rieur gauche ?? l'angle inf??rieur droit correspondent ?? la m??me puissance de x, et que les a-termes sont les coefficients du polyn??me (x + 1) ^n, et nous d??terminer les coefficients de (x + 1) ^{n 1.} Or, pour tout i 0 pas donn??e ou n + 1, le coefficient du terme x ⁱ dans le polyn??me (x + 1) ⁿ est ??gal ?? ¹ a _i (la figure ci-dessus et ?? la gauche de la figure pour d??terminer , puisque ce est sur la m??me diagonale) + un _i-1 (le chiffre ?? la droite imm??diate de la premi??re figure). Ce est en effet la r??gle simple pour construire triangle rang??e par rang??e de Pascal.

Il ne est pas difficile ?? tourner cet argument dans une preuve (par induction math??matique) du bin??me.

Une cons??quence int??ressante du th??or??me binomial est obtenu en r??glant les deux variables x et y ??gal ?? un. Dans ce cas, nous savons que $(1 + 1) = 2 ^ n ^ n$ , Et ainsi

${N \ choisissez 0} + {n \ choisissez 1} + \ cdots + {n \ choisir n-1} + {n \ n choisir} = 2 ^ n.$

En d'autres termes, la somme des entr??es de la n-i??me rang??e du triangle de Pascal est la n i??me puissance de deux.

Patterns et propri??t??s

Le triangle de Pascal poss??de de nombreuses propri??t??s et contient de nombreux mod??les de chiffres.

Les diagonales

Certains mod??les simples sont imm??diatement apparents dans les diagonales du triangle de Pascal:

Les diagonales passant le long des bords gauche et droit contiennent une seule de.
Les diagonales ?? c??t?? des diagonales de bord contiennent les nombres naturels dans l'ordre.
D??placement vers l'int??rieur, la prochaine paire de diagonales contient la nombres triangulaires dans l'ordre.
La prochaine paire de diagonales contient la t??tra??driques num??ros dans l'ordre, et la paire suivante donner num??ros de pentatope. En g??n??ral, chaque paire suivante de diagonales contient la dimension sup??rieure suivante "d - simplex "chiffres, qui peuvent ??tre d??finies comme

$\ Textrm {tri} _1 (n) = n \ quad \ mbox {et} \ quad \ textrm {tri} _ {d} (n) = \ sum_ {i = 1} ^ n \ mathrm {} _ {tri d -1} (i).$

Une autre formule est la suivante:

$\ Textrm {tri} _d (n) = \ begin {} cas 1 & \ mbox {if} d = 0 \\ n & \ mbox {} si d = 1 \\ \ displaystyle \ frac {1} {d!} \ prod_ {k = 0} ^ {d}-1 (n + k) & \ mbox {if} d \ ge 2. \ end {} cas$

La signification g??om??trique d'une fonction tri _d est: tri _d (1) = 1 pour tout j. Construire un d - dimensionnelle triangle (un triangle trois dimensions est un t??tra??dre ) en pla??ant des points suppl??mentaires en dessous d'un point initial, correspondant ?? tri _d (1) = 1. Placer ces points d'une mani??re analogue ?? l'emplacement des nombres dans le triangle de Pascal. Pour trouver _d tri (x), un total de x points qui composent la forme cible. tri _d (x) ??gale le nombre total de points dans la forme. Un triangle de dimension 1 est simplement une ligne, et par cons??quent, _une tri (x) = x, qui est la s??quence de nombres naturels. Le nombre de points dans chaque couche correspond ?? tri _{d - 1} (x).

Triangle de Sierpinski

Autres mod??les et propri??t??s

Le motif obtenu par la coloration que les nombres impairs dans le triangle de Pascal ressemble ??troitement ?? la fractale appel?? Triangle de Sierpinski, et cette ressemblance devient de plus en plus pr??cise que plusieurs lignes sont consid??r??es; ?? la limite, que le nombre de lignes se rapproche de l'infini, le motif r??sultant est le triangle de Sierpinski. Plus g??n??ralement, les num??ros pourraient ??tre color??es diff??remment selon si oui ou non ils sont multiples de 3, 4, etc .; il en r??sulte d'autres mod??les et combinaisons.

Imagine chaque nombre dans le triangle est un noeud dans un r??seau qui est connect?? aux num??ros adjacents sup??rieurs et inf??rieurs. Maintenant, pour ne importe quel n??ud de la grille, compter le nombre de chemins l?? dans la grille (sans revenir en arri??re) qui relient ce n??ud pour le n??ud sup??rieur (1) du triangle. La r??ponse est le nombre Pascal associ?? ?? ce noeud. L'interpr??tation du nombre dans le triangle de Pascal que le nombre de chemins ?? ce num??ro de la pointe signifie que sur un Plinko plateau de jeu en forme de triangle, la probabilit?? de gagner des prix plus pr??s du centre sera plus ??lev?? que gagner des prix sur les bords.

La valeur de chaque ligne, si chaque num??ro il est consid??r?? comme un lieu nombres d??cimaux et de plus de 9 sont report??s en cons??quence, est une puissance de 11 (plus pr??cis??ment, 11 ^n, o?? n est le num??ro de la ligne). Par exemple, la deuxi??me ligne indique ??1, 2, 1??, qui est de 11 ² (121). Dans la ligne de cinq, '1, 5, 10, 10, 5, 1' est traduit en 161051 apr??s avoir effectu?? les valeurs plus, ce qui est 11 ^5. Cette propri??t?? se explique facilement par la mise en x = 10 dans le d??veloppement du bin??me (x + 1) ^{le num??ro de ligne,} et en ajustant les valeurs pour se adapter dans le syst??me d??cimal.

Des mod??les plus subtiles

Il ya aussi plus surprenants, motifs subtils. D'un seul ??l??ment du triangle, une ligne diagonale plus superficielle peut ??tre form??e en d??pla??ant continuellement un ??l??ment vers la droite, puis un ??l??ment ?? en bas ?? droite, ou en allant dans la direction oppos??e. Un exemple est la ligne avec des ??l??ments 1, 6, 5, 1, ce qui commence ?? partir de la rang??e 1, 3, 3, 1 et se termine vers le bas trois rang??es. Un tel "diagonale" a une somme qui est un nombre de Fibonacci . Dans le cas de l'exemple, le nombre de Fibonacci est 13:

                                        1
                                     1 1
                                  1 2 1
                               1 → 3 ↓ 3 1
                            1 4 → 6 → 4 ↓ 1
                         1 5 10 10 → 5 → 1 ↓
                      → ↓ 1 6 15 20 15 6 1 →
                    1 7 → 21 35 35 21 7 1
                 1 8 28 56 70 56 28 8 1
               1 9 36 84 126 126 84 36 9 1
             1 10 45 120 210 252 210 120 45 10 1
           1 11 55 165 330 462 462 330 165 55 11 1
         1 12 66 220 495 792 924 792 495 220 66 12 1
       1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
     1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1 
   1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1

La deuxi??me soulign?? diagonale a une somme de 233. Les num??ros ??saut??s?? entre le droit de coup et le coup bas ?? droite ??galement vers??s aux nombres de Fibonacci, les num??ros ??tant ??entre?? les sommes form??s par la premi??re construction. Par exemple, les num??ros saut??es dans la premi??re diagonale sont mis en ??vidence 3, 4 et 1, ce qui rend 8.

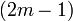En outre, si la ligne m est prise pour indiquer rang??e $(N + 1)$ , La somme des carr??s des ??l??ments de la rang??e m est ??gal ?? l'??l??ment central de la rang??e $(2m-1)$ . Par exemple, 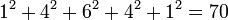$1 ^ 2 + 4 + 2 ^ 6 ^ 2 + 2 + 4 ^ 1 ^ 2 = 70$ . En forme g??n??rale:

$\ Sum_ {k = 0} ^ n {n \ choisir k} ^ 2 = {2n \ n} choisir.$

Un autre mod??le int??ressant est que sur ne importe quel m de la ligne, o?? m est impair, le moyen terme moins les deux points terme ?? gauche ??quivaut ?? une Nombre de Catalan, en particulier la (m + 1) / 2 nombre de Catalan. Par exemple: sur la ligne 5, 6-1 = 5, qui est la 3 ^e nombre de Catalan, et (5 + 1) / 2 = 3.

En outre, la somme des ??l??ments de la rang??e m est ??gal ?? 2 ^{m -1.} Par exemple, la somme des ??l??ments de la ligne 5 est 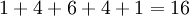$1 + 4 + 6 + 4 + 1 = 16$ , Qui est ??gal ?? 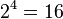$2 ^ 4 = 16$ . Cela d??coule du th??or??me binomial prouv?? ci-dessus, appliqu?? ?? (1 + 1) ^{m -1.}

Certains de ces num??ros dans le triangle de Pascal en corr??lation avec les num??ros Le triangle de Lozanić.

Une autre propri??t?? int??ressante du triangle de Pascal, ce est que dans les lignes o?? le deuxi??me nombre (1er num??ro suivant 1) est premier, tous les termes de cette ligne, sauf les 1s sont des multiples de ce premier.

Binomial matrice comme matrice exponentielle (illustration 5 ?? 5 matrices). Tous les points repr??sentent 0.

La matrice exponentielle

Gr??ce ?? sa construction simple par factorielles, une repr??sentation tr??s basique du triangle de Pascal en termes de matrice exponentielle peut ??tre donn??: le triangle de Pascal est l'exponentielle de la matrice qui a la s??quence 1, 2, 3, 4, ... sur la sous-diagonale et z??ro partout ailleurs.

Propri??t??s g??om??triques

Le triangle de Pascal peut ??tre utilis?? comme un table de consultation pour le nombre d'??l??ments dimensionn??s de fa??on arbitraire dans une seule version dimensionn??e de fa??on arbitraire un triangle (connu sous le nom simplex). Par exemple, consid??rez la 3??me ligne du triangle, avec les valeurs 1, 3, 3, 1. triangle A deux dimensions a un ??l??ment deux dimensions (lui-m??me), trois ??l??ments 1 dimensions (lignes, ou les bords), et trois ??l??ments de dimension 0 ( sommets, ou des coins). Le sens du nombre final (1) est plus difficile ?? expliquer (mais voir ci-dessous). Dans notre exemple, un t??tra??dre comporte un ??l??ment trois dimensions (elle-m??me), quatre ??l??ments de dimension 2 (faces), six ??l??ments de dimension 1 (bords), et quatre ??l??ments de dimension 0 (sommets). Ajout de la finale une fois de plus, ces valeurs correspondent ?? la 4??me ligne du triangle (1, 4, 6, 4, 1). Ligne 1 correspond ?? un point, et la ligne 2 correspond ?? un segment de ligne (dyade). Cette tendance se poursuit arbitrairement hyper-t??tra??dres haute-dimensionn?? (simplexes).

Pour comprendre pourquoi ce mod??le existe, il faut d'abord comprendre que le processus de construction d'un n -simplex d'une (n - 1) -simplex consiste ?? ajouter simplement un nouveau sommet ?? ce dernier, positionn?? de telle sorte que ce nouveau sommet se trouve en dehors de la l'espace de l'origine simplex, et le connecter ?? l'ensemble des sommets d'origine. A titre d'exemple, prenons le cas de la construction d'un t??tra??dre d'un triangle, ce dernier dont les ??l??ments sont ??num??r??s par ligne 3 de Pascal triangle: 1 visage, trois bords, et trois sommets (le sens de la finale 1 sera expliqu?? sous peu) . Pour construire un t??tra??dre d'un triangle, nous positionnons un nouveau sommet au-dessus du plan du triangle et connecter ce sommet ?? tous les trois sommets du triangle d'origine.

Le nombre de dimensions d'un ??l??ment donn?? dans le t??tra??dre est maintenant la somme de deux nombres: d'abord que le nombre d'??l??ment trouv?? dans le triangle original et le nombre de nouveaux ??l??ments, dont chacun est construit sur des ??l??ments d'une dimension de moins de la triangle d'origine. Ainsi, dans le t??tra??dre, le nombre de cellules (??l??ments poly??driques) est 0 (le triangle d'origine poss??de aucun) + 1 (construit sur la face unique du triangle d'origine) = 1; le nombre de faces est ??gal ?? 1 (le triangle original lui-m??me) + 3 (les nouvelles faces, chacune construite sur un bord du triangle d'origine) = 4; le nombre d'ar??tes est de 3 (du triangle d'origine) + 3 (les nouveaux bords, chacune construite sur un sommet du triangle d'origine) = 6; le nombre de nouveaux sommets est 3 (?? partir du triangle d'origine) + 1 (le nouveau sommet qui a ??t?? ajout?? pour cr??er le t??tra??dre du triangle) = 4. Ce processus de additionnant le nombre d'??l??ments d'une dimension donn??e ?? ceux d'une dimension moins pour arriver au nombre de l'ancien trouv?? dans la prochaine simplex sup??rieur est ??quivalent au processus de additionnant deux nombres adjacents dans une rang??e du triangle de Pascal pour produire le nombre ci-dessous. Ainsi, le sens du nombre final (1) dans une rang??e du triangle de Pascal devient comprise comme repr??sentant le nouveau sommet qui doit ??tre ajout?? ?? la simplex repr??sent??e par cette ligne pour obtenir la prochaine simplex sup??rieur repr??sent?? par la ligne suivante. Ce nouveau sommet est reli?? ?? chaque ??l??ment dans le simplex d'origine pour donner un nouvel ??l??ment d'une dimension sup??rieure ?? la nouvelle simplex, et ce est l'origine du motif trouv?? ??tre identique ?? celle observ??e dans le triangle de Pascal.

Une tendance similaire est observ??e relatives aux carr??s , par opposition ?? triangles. Pour trouver le mod??le, il faut construire un convertisseur analogique triangle de Pascal, dont les entr??es sont les coefficients de (x + 2) ^{Nombre de Row,} au lieu de (x + 1) ^{Nombre de Row.} Il ya deux fa??ons de le faire. Le plus simple est de commencer par la ligne 0 = 1 et en rang??e 1 = 1, 2. Proc??dez de construire les triangles analogiques selon la r??gle suivante:

${N \ choisir k = 2} \ times {n-1 \ choose k-1} + {n-1 \ choose k}.$

Ce est, choisissez une paire de nombres selon les r??gles du triangle de Pascal, mais le double celui sur la gauche avant d'ajouter. Il en r??sulte:

                              1
                          1 2
                      1 4 4
                  1 6 8 12
              1 8 24 32 16
          1 10 40 80 80 32
      1 12 60 160 240 192 64
  1 14 84 280 560 672 448 128

L'autre fa??on de fabrication de ce triangle est de commencer avec le triangle de Pascal et de multiplier chaque entr??e de 2 ^k, o?? k est la position dans la ligne d'un nombre donn??. Par exemple, la 2??me valeur la ligne 4 du triangle de Pascal est de 6 (la pente de 1s correspond ?? l'entr??e z??ro dans chaque ligne). Pour obtenir la valeur qui se trouve dans la position correspondante dans le triangle analogique, multiplier 6 par 2 ^{Nombre de position} = 6 ?? 2 ² = 6 x 4 = 24. Maintenant que le triangle analogique a ??t?? construit, le nombre d'??l??ments de ne importe quelle dimension que composer un arbitraire dimensionn?? cube (appel?? hypercube) peut ??tre lu ?? partir de la table d'une fa??on analogue ?? triangle de Pascal. Par exemple, le nombre d'??l??ments 2 dimensions dans un cube deux dimensions (un carr??) en est un, le nombre d'??l??ments 1 dimensions (c??t??s), ou des lignes est quatre, et le nombre d'??l??ments de dimension 0 (points, ou sommets) est 4. Cela correspond ?? la 2??me ligne de la table (1, 4, 4). Un cube poss??de une cube, six faces, douze ar??tes et huit sommets, qui correspond ?? la ligne suivante du triangle analogique (1, 6, 12, 8). Cette tendance se poursuit ind??finiment.

Pour comprendre pourquoi ce mod??le existe, reconna??t d'abord que la construction d'un n -cube d'une (n - 1) -cube est r??alis?? en dupliquant simplement la figure originale et la d??placer ?? une certaine distance (pour un n -cube r??guli??re, la longueur d'ar??te ) orthogonal ?? l'espace de la figure originale, alors la connexion de chaque sommet de la nouvelle valeur de son sommet correspondant de l'original. Ce processus de duplication initiale est la raison pour laquelle, d'??num??rer les ??l??ments dimensionnels d'un n -cube, il faut doubler le premier d'une paire de nombres dans une rang??e de cet analogue du triangle de Pascal avant de les additionner pour obtenir le num??ro ci-dessous. Le doublement initial donne ainsi le nombre d'??l??ments "originales" que l'on trouve dans le prochain n -cube sup??rieur et, comme avant, de nouveaux ??l??ments sont construits sur ceux d'une dimension moins (bords sur les sommets, des visages sur les bords, etc.). Encore une fois, le dernier num??ro d'une ligne repr??sente le nombre de nouveaux sommets ?? ajouter pour g??n??rer la prochaine sup??rieur n -cube.

Dans ce triangle, la somme des ??l??ments de la rang??e m est ??gal ?? 3 ^{m - une} fois de plus, d'utiliser les ??l??ments de la ligne 5 ?? titre d'exemple.: 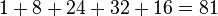$1 + 8 + 24 + 32 + 16 = 81$ , Qui est ??gal ?? $3 ^ 4 = 81$ .

Yang Hui le triangle (Pascal), tel que repr??sent?? par les Chinois ?? l'aide num??ros de tige.

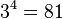Le calcul d'une ligne individuelle

Cet algorithme est une alternative ?? la m??thode standard de calcul de cellules individuelles avec factorielles. ?? partir de la gauche, la valeur de la premi??re cellule est 1. Pour chaque cellule apr??s, la valeur est d??termin??e en multipliant la valeur vers la gauche par une fraction de changer lentement:

$v (c) = \ frac {r-c} {c}$

O?? r = ligne + 1, en commen??ant par 0 au sommet, et c = la colonne, en commen??ant par 0 sur la gauche. Par exemple, pour calculer la ligne 5, r = 6. La premi??re valeur est 1. La valeur suivante est de 1 x 5/1 = 5. Le num??rateur diminue d'un, et le d??nominateur augmente de un ?? chaque ??tape. Donc 5 x 4/2 = 10. Puis 10 x 3/3 = 10. Puis 10 x 2/4 = 5. Puis 5 x 1/5 = 1. Notez que la derni??re cellule est toujours ??gale ?? 1, la multiplication final est inclus pour l'int??gralit?? de la s??rie.

Une tendance similaire existe sur une diagonale vers le bas. ?? partir de l'un et le nombre naturel dans la cellule voisine, forment une fraction. Pour d??terminer la cellule suivante, augmenter le num??rateur et le d??nominateur chacun par un, puis multiplier le r??sultat par la fraction pr??c??dente. Par exemple, la ligne commen??ant par 1 et 7 forment une fraction de 7/1. La cellule suivante est 7 x 8/2 = 28. La cellule suivante est 28 x 84 = 3.9.

Notez que pour une ligne individuelle vous ne devez calculer la moiti?? (arrondi) le nombre de valeurs dans la rang??e. Ce est parce que la ligne est sym??trique.

Histoire

Les premi??res repr??sentations explicites d'un triangle de coefficients binomiaux se produisent dans le 10??me si??cle dans les commentaires sur le Chandas Shastra, un ancien livre indien sur sanscrit prosodie ??crit par Pingala entre le 5th- 2??me si??cle avant JC. Alors que le travail de Pingala ne survit que dans des fragments, le commentateur Halayudha, autour de 975, utilis?? le triangle d'expliquer r??f??rences obscures ?? Meru-prastaara, le "Escalier de Mont Meru ". Il a ??galement rendu compte que les diagonales peu profondes de la somme de triangle aux nombres de Fibonacci . Le math??maticien indien Bhattotpala (c. 1068) donne par la suite des lignes 0-16 du triangle.

?? peu pr??s au m??me moment, il a ??t?? discut?? dans la Perse ( Iran ) par le math??maticien Al-Karaji (953-1029) et le po??te - astronome math??maticien Omar Khayyam (1048-1131); donc le triangle est appel?? le "triangle Khayyam" en Iran . Plusieurs th??or??mes li??s au triangle connues, y compris la bin??me. En fait, nous pouvons ??tre assez s??r que Khayyam a utilis?? une m??thode de trouver n i??me racines sur la base du d??veloppement du bin??me, et donc sur les coefficients binomiaux.

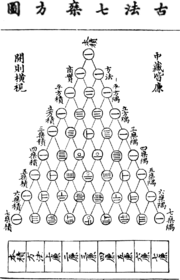
Au 13??me si??cle, Yang Hui (1238-1298) pr??sent?? le triangle arithm??tique, qui ??tait le m??me que le triangle de Pascal . Aujourd'hui, le triangle de Pascal est appel?? " Le triangle de Yang Hui "en Chine .

Enfin, en Italie , il est appel?? "le triangle de Tartaglia", du nom de l'alg??briste italienne Niccol?? Fontana Tartaglia qui a v??cu un si??cle avant Pascal (1500-1577); Tartaglia est cr??dit?? de la formule g??n??rale pour r??soudre polyn??mes cubiques (qui peut ??tre vraiment partir Scipione del Ferro, mais a ??t?? publi?? par J??r??me Cardan 1545).

Petrus Apianus (1495 -1552) a publi?? le Triangle sur le frontispice de son livre sur les calculs d'affaires de 1531 ?? 1532 et une version ant??rieure en 1527 le premier enregistrement de celui-ci en Europe.

En 1655, Blaise Pascal a ??crit un Trait?? du triangle arithm??tique (Trait?? sur triangle arithm??tique), dans laquelle il a recueilli plusieurs r??sultats connus ?? l'??poque sur le triangle, et les employ??s pour r??soudre les probl??mes de la th??orie des probabilit??s . Le triangle a ensuite ??t?? nomm?? d'apr??s Pascal par Pierre R??mond de Montmort (1708) et Abraham de Moivre (1730).

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Pascal%27s_triangle&oldid=208833303 "