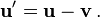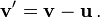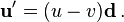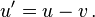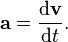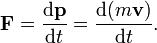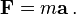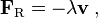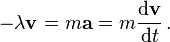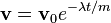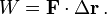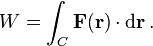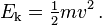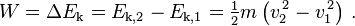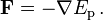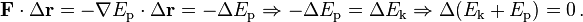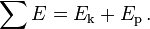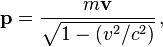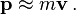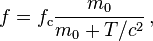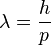La mec??nica cl??sica

Temas relacionados: Matem??ticas ; Ciencias

Antecedentes

SOS cree que la educaci??n da una mejor oportunidad en la vida para los ni??os en el mundo en desarrollo tambi??n. Haga clic aqu?? para obtener m??s informaci??n sobre SOS Children.

La mec??nica cl??sica
Historia Cronolog??a
Ramas Est??tica Din??mica Cin??tica Cinem??tica Mec??nica Aplicada Mec??nica celeste Mec??nica de medios continuos La mec??nica estad??stica
Formulaciones Mec??nica newtoniana (Vectorial mec??nica) Mec??nica anal??tica ( Mec??nica lagrangiana Mec??nica hamiltoniana)
Conceptos fundamentales Espacio Tiempo Masa Inercia Velocidad Velocidad Aceleraci??n Fuerza Impulso Impulso Par / Momento / Pareja El momento angular Momento de inercia Marco de referencia Energ??a ( cin??tica potencial) El trabajo mec??nico La energ??a mec??nica Trabajo virtual Principio de D'Alembert
Temas b??sicos Cuerpo r??gido ( din??mica Ecuaciones de Euler) Motion ( lineal) Leyes de Euler del movimiento Leyes de Newton Ley de Newton gravitaci??n universal Ecuaciones del movimiento Inercial / No inercial marco de referencia Fuerza ficticia Mec??nica de planar movimiento de las part??culas Desplazamiento (vector) Velocidad relativa Fricci??n Movimiento arm??nico simple Oscilador arm??nico Vibraci??n Damping ( ratio)
El movimiento de rotaci??n Movimiento circular ( uniforme no uniforme) Rotaci??n de marco de referencia Fuerza centr??peta Fuerza centr??fuga ( giratoria marco de referencia reactiva) Fuerza de Coriolis P??ndulo Tangente / Velocidad rotacional Aceleraci??n angular Velocidad angular La frecuencia angular El desplazamiento angular
Los cient??ficos Galileo Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel / Johann Bernoulli Cauchy

En la f??sica , la mec??nica cl??sica es una de las dos principales sub-campos de la la mec??nica, que tiene que ver con el conjunto de leyes f??sicas que describen el movimiento de cuerpos bajo la acci??n de un sistema de fuerzas. El estudio del movimiento de los cuerpos es muy antigua, por lo que la mec??nica cl??sica de uno de los temas m??s antiguos y m??s grandes de la ciencia , la ingenier??a y la tecnolog??a .

La mec??nica cl??sica describe el movimiento de objetos macrosc??picos, desde proyectiles a partes de maquinaria, as?? como objetos astron??micos, tales como veh??culos espaciales, planetas , estrellas y galaxias . Adem??s de esto, muchas especializaciones dentro del tema tratan con los gases , l??quidos , s??lidos y otros subtemas espec??ficos. La mec??nica cl??sica proporciona resultados muy precisos, siempre y cuando el dominio de estudio se limita a los objetos grandes y las velocidades involucradas no se acercan a la velocidad de la luz . Cuando los objetos se tratan convertido suficientemente peque??o, se hace necesario introducir el otro mayor sub-campo de la mec??nica, la mec??nica cu??ntica , que reconcilia las leyes macrosc??picas de la f??sica con la naturaleza at??mica de la materia y se encarga de la la dualidad onda-part??cula de ??tomos y mol??culas . En el caso de altas velocidades objetos se acercan a la velocidad de la luz, la mec??nica cl??sica se ve reforzada por la relatividad especial . La relatividad general unifica la relatividad especial con La ley de Newton de la gravitaci??n universal, lo que permite a los f??sicos a manejar la gravitaci??n a un nivel m??s profundo.

El t??rmino mec??nica cl??sica fue acu??ado en el siglo 20 para describir el sistema de la f??sica iniciada por Isaac Newton y muchos contempor??nea del siglo 17 fil??sofos de la naturaleza, bas??ndose en las teor??as astron??micas anteriores de Johannes Kepler , que a su vez se basa en las observaciones precisas de Tycho Brahe y los estudios de la terrestre movimiento de proyectiles de Galileo . Desde la construcci??n de estos aspectos de la f??sica mucho antes de la aparici??n de la f??sica cu??ntica y la relatividad, algunas fuentes excluyen de Einstein la teor??a de la relatividad de esta categor??a. Sin embargo, un n??mero de fuentes modernas s?? incluyen la mec??nica relativista, que a su juicio representa la mec??nica cl??sica en su forma m??s desarrollada y m??s preciso.

La etapa inicial en el desarrollo de la mec??nica cl??sica se refiere a menudo como la mec??nica de Newton, y se asocia con los conceptos empleados por f??sicos y los m??todos matem??ticos inventados por el propio Newton, en paralelo con Leibniz , y otros. Esto se describe con m??s detalle en las siguientes secciones. M??s tarde, se desarrollaron m??todos m??s abstractos y generales, que lleva a la reformulaci??n de la mec??nica cl??sica conocido como Mec??nica lagrangiana y Mec??nica hamiltoniana. Estos avances se hicieron en gran parte en los siglos 18 y 19, y se extienden sustancialmente m??s all?? del trabajo de Newton, en particular mediante el uso de mec??nica anal??tica. En ??ltima instancia, las matem??ticas desarrolladas para estos eran fundamentales para la creaci??n de la mec??nica cu??ntica.

Historia

Algunos Fil??sofos griegos de la antig??edad, entre ellos Arist??teles , fundador de La f??sica aristot??lica, puede haber sido el primero en mantener la idea de que "todo sucede por una raz??n" y que los principios te??ricos pueden ayudar en la comprensi??n de la naturaleza. Mientras que para un lector moderno, muchas de estas ideas conservados saldr?? como eminentemente razonable, hay una falta evidente de ambos matem??tica teor??a y controlada experimentar, tal como la conocemos. Estos dos resultaron ser factores decisivos en la formaci??n de la ciencia moderna, y que comenzaron con la mec??nica cl??sica.

La "ciencia de pesos" medieval (es decir, la mec??nica) debe gran parte de su importancia para el trabajo de Jordanus Nemorarius. En el Elementa ponderum s??per demonstrationem, se introduce el concepto de "posicional gravedad "y el uso de componentes de fuerzas .

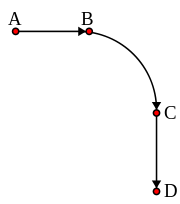
Tres estadios Teor??a de impulso seg??n Alberto de Sajonia.

El primero publicado explicaci??n causal de los movimientos de los planetas fue Johannes Kepler Astronomia nova public?? en 1609. Lleg?? a la conclusi??n, basada en Observaciones de Tycho Brahe de la ??rbita de Marte , que las ??rbitas eran elipses. Esta ruptura con pensamiento antiguo estaba ocurriendo alrededor del mismo tiempo que Galileo estaba proponiendo leyes matem??ticas abstractas para el movimiento de los objetos. ??l puede (o no) han realizado el famoso experimento de dejar caer dos bolas de ca????n de diferentes pesos de la torre de Pisa , mostrando que ambos cayeron al piso al mismo tiempo. La realidad de este experimento se disputa, pero, m??s importante a??n, ??l llev?? a cabo experimentos cuantitativos por bolas rodando sobre una plano inclinado. Su teor??a de movimiento acelerado deriva de los resultados de tales experimentos, y forma una piedra angular de la mec??nica cl??sica.

Sir Isaac Newton (1643-1727), una figura influyente en la historia de la f??sica y cuyos tres leyes del movimiento constituir la base de la mec??nica cl??sica

Como fundamento de sus principios de la filosof??a natural, Isaac Newton propuso tres leyes del movimiento : el ley de la inercia , la segunda ley de la aceleraci??n (mencionado anteriormente), y la ley de acci??n y reacci??n; y de ah?? sentado las bases de la mec??nica cl??sica. Tanto las leyes segundo y tercero de Newton se les dio tratamiento cient??fico y matem??tico adecuado en Newton Philosophi?? Naturalis Principia Mathematica, que los distingue de los anteriores intentos de explicar los fen??menos similares, que eran incompletas, incorrectas, o dado poca expresi??n matem??tica precisa. Newton tambi??n enunci?? los principios de conservaci??n del momento y momento angular . En mec??nica, Newton tambi??n fue el primero en proporcionar la primera formulaci??n cient??fica y matem??tica correcta de gravedad en La ley de Newton de la gravitaci??n universal. La combinaci??n de las leyes del movimiento y la gravitaci??n de Newton proporciona la descripci??n m??s completa y precisa de la mec??nica cl??sica. Demostr?? que estas leyes se aplican a los objetos cotidianos, as?? como a los objetos celestes. En particular, se obtiene una explicaci??n te??rica de las leyes de Kepler del movimiento de los planetas.

Newton previamente invent?? el c??lculo , de las matem??ticas, y lo utiliz?? para realizar los c??lculos matem??ticos. Para aceptabilidad, su libro, el Principia , se formul?? en su totalidad en t??rminos de los m??todos geom??tricos de larga data, que pronto fueron eclipsadas por su c??lculo. Sin embargo, fue Leibniz quien desarroll?? la notaci??n del derivado y integral hoy preferido.

La mayor contribuci??n de Hamilton es quiz??s la reformulaci??n de la mec??nica de Newton , que ahora se llama Mec??nica hamiltoniana.

Newton, y la mayor??a de sus contempor??neos, con la notable excepci??n de Huygens, trabajaron en el supuesto de que la mec??nica cl??sica ser??a capaz de explicar todos los fen??menos, incluyendo la luz , en forma de la ??ptica geom??trica. Incluso al descubrir la llamada Anillos de Newton (un interferencia de ondas fen??meno) su explicaci??n se qued?? con su propia la teor??a corpuscular de la luz.

Despu??s de Newton, la mec??nica cl??sica se convirti?? en un campo principal de estudio en matem??ticas, as?? como la f??sica. Despu??s de Newton, varias reformulaciones permite progresivamente la b??squeda de soluciones a un n??mero mucho mayor de problemas. La primera notable re-formulaci??n fue en 1788 por Joseph Louis Lagrange . Mec??nica lagrangiana fue a su vez re-formulados en 1833 por William Rowan Hamilton.

Algunas dificultades fueron descubiertos en el siglo 19 que s??lo puede ser resuelto por la f??sica m??s moderna. Algunas de estas dificultades relacionadas con la compatibilidad con la teor??a electromagn??tica , y el famoso Experimento de Michelson-Morley. La resoluci??n de estos problemas llevaron a la teor??a especial de la relatividad , incluye a menudo en la mec??nica cl??sica plazo.

Un segundo conjunto de dificultades que estaban relacionados con la termodin??mica. Cuando se combina con la termodin??mica , la mec??nica cl??sica lleva a la Gibbs paradoja de la cl??sica mec??nica estad??stica , en los que la entrop??a no es una cantidad bien definida. La radiaci??n del cuerpo negro no se explica sin la introducci??n de cuantos. Como experimentos alcanzaron el nivel at??mico, la mec??nica cl??sica no pudo explicar, ni siquiera aproximadamente, cosas tan b??sicas como la los niveles de energ??a y tama??os de los ??tomos y la efecto fotoel??ctrico. El esfuerzo en la soluci??n de estos problemas condujo al desarrollo de la mec??nica cu??ntica .

Desde finales del siglo 20, el lugar de la mec??nica cl??sica en la f??sica ha sido ya no el de una teor??a independiente. En su lugar, la mec??nica cl??sica se considera ahora una teor??a aproximada a la mec??nica cu??ntica m??s generales. El ??nfasis se ha desplazado a la comprensi??n de las fuerzas fundamentales de la naturaleza como en el modelo est??ndar y sus extensiones m??s modernas en un unificado teor??a del todo. La mec??nica cl??sica es una teor??a para el estudio del movimiento de las part??culas no-mec??nica cu??ntica, de baja energ??a en campos gravitatorios d??biles. En la mec??nica cl??sica del siglo 21 se ha ampliado en el dominio complejo y la mec??nica cl??sica complejos exhibe comportamientos muy similares a la mec??nica cu??ntica.

Descripci??n de la teor??a

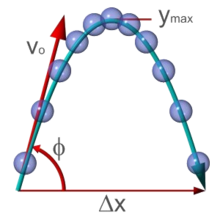
El an??lisis de movimiento de un proyectil es una parte de la mec??nica cl??sica.

A continuaci??n se presentan los conceptos b??sicos de la mec??nica cl??sica. Para simplificar, a menudo modelos objetos del mundo real como part??culas puntuales, los objetos con tama??o insignificante. El movimiento de una part??cula punto se caracteriza por un peque??o n??mero de par??metros: su posici??n, masa , y las fuerzas que se le aplican. Cada uno de estos par??metros se discute en turno.

En realidad, el tipo de objetos que la mec??nica cl??sica puede describir siempre tienen un no-cero tama??o. (La f??sica de part??culas muy peque??as, como el electr??n , se describe con mayor precisi??n por la mec??nica cu??ntica ). Los objetos con tama??o distinto de cero tienen un comportamiento m??s complicado que las part??culas punto hipot??tico, debido a la adicional grados de libertad para ejemplo, un b??isbol puede girar mientras se est?? moviendo. Sin embargo, los resultados para part??culas puntuales se pueden utilizar para estudiar tales objetos trat??ndolos como objetos compuestos, compuestos por un gran n??mero de part??culas que interact??an de punto. El centro de masa de un objeto compuesto se comporta como una part??cula puntual.

Usos mec??nica cl??sica existen e interact??an nociones de sentido com??n de c??mo la materia y las fuerzas. Se asume que la materia y la energ??a tienen atributos definidos, conocibles tales como que un objeto est?? en el espacio y su velocidad. Tambi??n se supone que los objetos pueden estar directamente influidos s??lo por su entorno inmediato, conocido como el principio de localidad. En la mec??nica cu??ntica objetos pueden tener posici??n incognoscible o velocidad, o instant??neamente interactuar con otros objetos a distancia.

Posici??n y sus derivados

La Derivadas SI "mec??nica" (Es decir, no electromagn??tica o t??rmica) unidades con kg, m y s
posici??n	m
posici??n angular / ??ngulo	sin unidades (radian)
velocidad	m ?? ^{s -1}
velocidad angular	s ^-1
aceleraci??n	m ?? ^{s -2}
aceleraci??n angular	s ^-2
tir??n	m ?? ^{s -3}
"Jerk angular"	s ^-3
energ??a espec??fica	m ² ?? ^{s -2}
tasa de dosis absorbida	m ² ?? ^{s -3}
momento de inercia	kg ?? m ²
impulso	kg ?? m ?? s ^-1
momento angular	kg ?? m ² ?? s ^-1
fuerza	kg ?? m ?? s ^-2
esfuerzo de torsi??n	kg ?? m ² ?? s ^-2
energ??a	kg ?? m ² ?? s ^-2
energ??a	kg ?? m ² ?? s ^-3
presi??n y densidad de energ??a	kg ?? ^{m -1} ?? ^{s -2}
tensi??n superficial	kg ?? ^{s -2}
constante de resorte	kg ?? ^{s -2}
irradiancia y flujo de energ??a	kg ?? ^{s -3}
viscosidad cinem??tica	m ² ?? ^{s -1}
viscosidad din??mica	kg ?? ^{m -1} ?? ^{s -1}
la densidad (densidad de masa)	kg ?? ^{m -3}
la densidad (densidad peso)	kg ?? ^m-2 ?? ^{s -2}
densidad num??rica	m ^-3
acci??n	kg ?? m ² ?? s ^-1

La posici??n de una punto de part??cula se define con respecto a un punto de referencia fijo arbitrario, O, en espacio, por lo general acompa??ado por un sistema de coordenadas, con el punto de referencia situado en el origen del sistema de coordenadas. Se define como el vector r de O a la part??cula. En general, la part??cula punto no necesita ser estacionaria con respecto a O, por lo que r es una funci??n de t, el tiempo transcurrido desde un tiempo inicial arbitrario. En pre-Einstein de la relatividad (conocido como La relatividad de Galileo), el tiempo se considera un absoluto, es decir, el intervalo de tiempo entre cualquier par dado de eventos es la misma para todos los observadores. Adem??s de confiar en tiempo absoluto, la mec??nica cl??sica asume la geometr??a euclidiana para la estructura del espacio.

La velocidad y la velocidad

La velocidad , o la velocidad de cambio de la posici??n con el tiempo, se define como la derivada de la posici??n con respecto al tiempo o

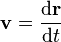$\ Mathbf {v} = {\ mathrm {d} \ mathbf {r} \ sobre \ mathrm {d} t} \, \!$ .

En la mec??nica cl??sica, las velocidades son directamente aditivo y sustractivo. Por ejemplo, si un autom??vil que viaja hacia el este a 60 kmh pasa otro coche en direcci??n este a 50 km / h, a continuaci??n, desde la perspectiva del coche m??s lento, el coche m??s r??pido se desplaza hacia el este a 60-50 = 10 km / h. Considerando que, desde la perspectiva del coche m??s r??pido, el coche m??s lento se mueve 10 kmh al oeste. Las velocidades son directamente aditivo seg??n magnitudes vectoriales; deben ser tratadas con el uso de an??lisis vectorial .

Matem??ticamente, si la velocidad del primer objeto en la discusi??n anterior se denota por el vector u = u d y la velocidad de la segunda objeto por el vector v = v e, donde u es la velocidad de la primera objeto, v es la velocidad del segundo objeto, y D y E son vectores unitarios en las direcciones de movimiento de cada part??cula, respectivamente, entonces la velocidad del primer objeto, como se ve por el segundo objeto es

$\ Mathbf {u} = \ vec {u} - \ mathbf {v} \,.$

Del mismo modo,

$\ Mathbf {v '} = \ mathbf {v} - \ mathbf {u} \,.$

Cuando ambos objetos se mueven en la misma direcci??n, esta ecuaci??n se puede simplificar a

$\ Mathbf {u} '= (u - v) \ mathbf {d} \,.$

O, haciendo caso omiso de direcci??n, la diferencia puede ser dado en t??rminos de s??lo la velocidad:

$u '= u - v \,.$

Aceleraci??n

La aceleraci??n , o la tasa de cambio de la velocidad, es el derivado de la velocidad con respecto al tiempo (la segunda derivada de la posici??n con respecto al tiempo) o

$\ Mathbf {a} = {\ mathrm {d} \ mathbf {v} \ sobre \ mathrm {d} t}.$

La aceleraci??n puede surgir de un cambio con el tiempo de la magnitud de la velocidad o de la direcci??n de la velocidad o ambos. Si s??lo la magnitud v de la velocidad disminuye, esto se refiere a veces como la desaceleraci??n, pero en general, cualquier cambio en la velocidad con el tiempo, incluyendo la desaceleraci??n, se refiere simplemente como la aceleraci??n.

Fuerzas; La segunda ley de Newton

Newton fue el primero en expresar matem??ticamente la relaci??n entre la fuerza y el ??mpetu . Algunos f??sicos interpretan segunda ley del movimiento de Newton como una definici??n de la fuerza y la masa, mientras que otros consideran que es un postulado fundamental, una ley de la naturaleza. De cualquier interpretaci??n tiene las mismas consecuencias matem??ticas, hist??ricamente conocido como "La Segunda Ley de Newton":

$\ Mathbf {F} = {\ mathrm {d} \ mathbf {p} \ sobre \ mathrm {d} t} = {\ mathrm {d} (m \ mathbf {v}) \ over \ mathrm {d} t} .$

La cantidad m v se llama el ( can??nica) impulso . La fuerza neta sobre una part??cula es por lo tanto igual a la tasa de cambio de impulso de la part??cula con el tiempo. Dado que la definici??n de aceleraci??n es a = d v / d t, la segunda ley puede escribirse en forma simplificada y m??s familiar:

$\ Mathbf {F} = m \ mathbf {a} \,.$

Mientras se conoce la fuerza que act??a sobre una part??cula, la segunda ley de Newton es suficiente para describir el movimiento de una part??cula. Una vez que las relaciones independientes para cada fuerza que act??a sobre una part??cula est??n disponibles, pueden ser sustituidos en la segunda ley de Newton para obtener una ecuaci??n diferencial ordinaria , que se llama la ecuaci??n de movimiento.

Como ejemplo, supongamos que la fricci??n es la ??nica fuerza que act??a sobre la part??cula, y que puede ser modelado como una funci??n de la velocidad de la part??cula, por ejemplo:

$\ Mathbf {F} _ {\ rm R} = - \ lambda \ mathbf {v} \,,$

donde λ es una constante positiva. Entonces la ecuaci??n de movimiento es

$- \ Lambda \ mathbf {v} = m \ mathbf {a} = m {\ mathrm {d} \ mathbf {v} \ sobre \ mathrm {d} t} \,.$

Esto puede ser integrada para obtener

$\ Mathbf {v} = \ mathbf {v} _0 e ^ {- \ lambda t / m}$

donde v ₀ es la velocidad inicial. Esto significa que la velocidad de esta part??cula decae exponencialmente a cero a medida que avanza el tiempo. En este caso, un punto de vista equivalente es que la energ??a cin??tica de la part??cula es absorbida por la fricci??n (que la convierte en calor la energ??a de acuerdo con la conservaci??n de la energ??a), frenarla. Esta expresi??n puede integrarse adicionalmente para obtener la posici??n r de la part??cula como una funci??n del tiempo.

Fuerzas importantes incluyen la fuerza de la gravedad y la Fuerza de Lorentz para el electromagnetismo . Adem??s, la tercera ley de Newton a veces se puede utilizar para deducir las fuerzas que act??an sobre una part??cula: si se sabe que la part??cula A ejerce una fuerza F sobre otra part??cula B, se deduce que B debe ejercer una fuerza de reacci??n igual y opuesta, - F , en A. La forma fuerte de la tercera ley de Newton requiere que F y - F acto lo largo de la l??nea que une A y B, mientras que la forma d??bil no lo hace. Ilustraciones de la forma d??bil de la tercera ley de Newton se encuentran a menudo por fuerzas magn??ticas.

Trabajo y energ??a

Si una fuerza constante F se aplica a una part??cula que logra un desplazamiento Δ r, el trabajo realizado por la fuerza se define como la producto escalar de los vectores de fuerza y desplazamiento:

$W = \ mathbf {F} \ cdot \ Delta \ mathbf {r} \,.$

M??s en general, si la fuerza var??a como una funci??n de la posici??n que la part??cula se mueve de r a r _{1 2} a lo largo de una trayectoria C, el trabajo realizado sobre la part??cula est?? dada por la integral de l??nea

$W = \ int_C \ mathbf {F} (\ mathbf {r}) \ cdot \ mathrm {d} \ mathbf {r} \,.$

Si el trabajo realizado en el movimiento de la part??cula de R ₁ a R ₂ es el mismo sin importar qu?? camino le consta a la fuerza se dice que es conservador. La gravedad es una fuerza conservadora, como es la fuerza debida a una idealizada primavera, como se da por La ley de Hooke. La fuerza debida a la fricci??n es no conservadora.

La energ??a cin??tica E _k de una part??cula de masa m que viaja a la velocidad v est?? dada por

$E_ \ mathrm {k} = \ tfrac {1} {2} mv ^ 2 \,.$

Para objetos extendidos compuestos por muchas part??culas, la energ??a cin??tica del cuerpo compuesto es la suma de las energ??as cin??ticas de las part??culas.

El teorema de trabajo-energ??a establece que para que una part??cula de masa constante m el trabajo total W realizado sobre la part??cula de posici??n r ₁ r ₂ es igual a la variaci??n de la energ??a cin??tica E _k de la part??cula:

$W = \ Delta E_ \ mathrm {k} = E_ \ mathrm {k, 2} - E_ \ mathrm {k, 1} = \ tfrac {1} {2} m \ left (v_2 ^ {\, 2} - v_1 ^ {\, 2} \ right) \,.$

Las fuerzas conservadoras se pueden expresar como la gradiente de una funci??n escalar, conocido como el energ??a potencial y denotado E _p:

$\ Mathbf {F} = - \ mathbf {\ nabla} E_ \ mathrm {p} \,.$

Si todas las fuerzas que act??an sobre una part??cula son conservadores, y E _p es el total energ??a potencial (que se define como una obra de fuerzas involucradas para reorganizar posiciones mutuas de los ??rganos), que se obtiene sumando las energ??as potenciales correspondientes a cada fuerza

$\ Mathbf {F} \ cdot \ Delta \ mathbf {r} = - \ mathbf {\ nabla} E_ \ mathrm {p} \ cdot \ Delta \ mathbf {r} = - \ Delta E_ \ mathrm {p} \ Rightarrow - \ Delta E_ \ mathrm {p} = \ Delta E_ \ mathrm {k} \ Rightarrow \ Delta (E_ \ mathrm {k} + E_ \ mathrm {p}) = 0 \,.$

Este resultado se conoce como la conservaci??n de la energ??a y establece que el total de la energ??a ,

$\ Suma E = E_ \ mathrm {k} + E_ \ mathrm {p} \,.$

es constante en el tiempo. A menudo es ??til, porque muchas fuerzas com??nmente encontrados son conservadoras.

M??s all?? de las leyes de Newton

La mec??nica cl??sica tambi??n incluye descripciones de los complejos movimientos de los objetos no puntuales extendidas. Leyes de Euler proporcionan extensiones a las leyes de Newton en este ??mbito. Los conceptos de momento angular se basan en el mismo c??lculo se utiliza para describir el movimiento unidimensional. La ecuaci??n cohete se extiende el concepto de velocidad de cambio de impulso de un objeto para incluir los efectos de un objeto "p??rdida de masa".

Hay dos importantes formulaciones alternativas de la mec??nica cl??sica: Mec??nica lagrangiana y Mec??nica hamiltoniana. Estas, y otras formulaciones modernas, por lo general pasan por alto el concepto de "fuerza", en vez refiri??ndose a otras magnitudes f??sicas, como la energ??a, la velocidad y el momento, para la descripci??n de los sistemas mec??nicos en coordenadas generalizadas.

Las expresiones dadas anteriormente para el impulso y la energ??a cin??tica s??lo son v??lidos cuando no hay una contribuci??n significativa electromagn??tica. En el electromagnetismo, la segunda ley de Newton para cables conductores de corriente se rompe menos uno incluye la contribuci??n del campo electromagn??tico al impulso del sistema seg??n lo expresado por el Vector de Poynting divide por ² c, donde c es la velocidad de la luz en el espacio libre.

L??mites de validez

Dominio de validez de la Mec??nica Cl??sica

Muchas ramas de la mec??nica cl??sica son simplificaciones o aproximaciones de las formas m??s exactos; dos de los m??s precisos siendo la relatividad general y relativistas mec??nica estad??stica . La ??ptica geom??trica es una aproximaci??n a la la teor??a cu??ntica de la luz, y no tiene una forma "cl??sica" superior.

La aproximaci??n newtoniana a la relatividad especial

En la relatividad especial, el momento de una part??cula viene dada por

$\ Mathbf {p} = \ frac {m \ mathbf {v}} {\ sqrt {1- (v ^ 2 / c ^ 2)}} \,,$

donde m es la masa en reposo de la part??cula, v su velocidad, y c es la velocidad de la luz.

Si v es muy peque??o en comparaci??n con c, v ² / c ² es aproximadamente cero, y as??

$\ Mathbf {p} \ aprox m \ mathbf {v} \,.$

As??, la ecuaci??n newtoniana p = m v es una aproximaci??n de la ecuaci??n relativista para cuerpos que se mueven con velocidades bajas en comparaci??n con la velocidad de la luz.

Por ejemplo, la frecuencia de ciclotr??n relativista de una ciclotr??n, girotr??n, o de alta tensi??n magnetr??n est?? dada por

$f = f_ \ mathrm {c} \ frac {} {m_0 m_0 + T / c ^ 2} \,,$

donde f es la frecuencia _c cl??sica de un electr??n (o de otra part??cula cargada) con cin??tica de energ??a y T ( descanso) masa m ₀ rodeando en un campo magn??tico. El (resto) masa de un electr??n es 511 keV. As?? que la correcci??n de la frecuencia es de 1% para un tubo de vac??o magn??tico con una tensi??n de corriente continua 5,11 kV de aceleraci??n.

La aproximaci??n cl??sica a la mec??nica cu??ntica

El modelo de rayos de la mec??nica cl??sica se rompe cuando el longitud de onda de De Broglie no es mucho menor que otras dimensiones del sistema. Para part??culas no relativistas, esta longitud de onda es

$\ Lambda = \ frac {h} {p}$

donde h es P constante de Planck es el impulso.

Una vez m??s, esto ocurre con los electrones antes de que suceda con las part??culas m??s pesadas. Por ejemplo, los electrones utilizados por Clinton Davisson y Lester Germer en 1927, acelerado por 54 voltios, ten??a una longitud de onda de 0.167 nm, lo que fue suficiente para exhibir un solo difracci??n l??bulo lateral al reflexionar desde la cara de una moneda de cristal con un espaciado at??mico de 0.215 nm. Con un mayor c??mara de vac??o, parecer??a relativamente f??cil de aumentar la resoluci??n angular de todo un radian a una difracci??n cu??ntica miliradi??n y ver en los patrones peri??dicos de circuito integrado de memoria del ordenador.

Los ejemplos m??s pr??cticos del fracaso de la mec??nica cl??sica en una escala de ingenier??a son la conducci??n por t??nel cu??ntico en diodos t??nel y muy estrecho transistor puertas en circuitos integrados .

La mec??nica cl??sica es el mismo extremo aproximaci??n de alta frecuencia como la ??ptica geom??trica. Es m??s a menudo precisa porque describe part??culas y cuerpos con masa en reposo. Estos tienen m??s impulso y por lo tanto m??s cortas longitudes de onda de De Broglie que las part??culas sin masa, como la luz, con las mismas energ??as cin??ticas.

Ramas

Las ramas de la mec??nica

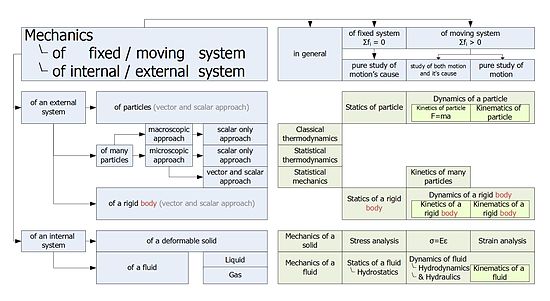
La mec??nica cl??sica fue dividido tradicionalmente en tres ramas principales:

Est??tica, el estudio de equilibrio y su relaci??n con las fuerzas
Din??mica, el estudio del movimiento y su relaci??n con las fuerzas
Cinem??tica , frente a las consecuencias de movimientos observados sin tener en cuenta las circunstancias caus??ndoles

Otra divisi??n se basa en la elecci??n de formalismo matem??tico:

Mec??nica newtoniana
Mec??nica lagrangiana
Mec??nica hamiltoniana

Alternativamente, una divisi??n puede ser hecha por regi??n de aplicaci??n:

La mec??nica celeste, en relaci??n con estrellas , planetas y otros cuerpos celestes
Mec??nica de medios continuos, para materiales modelados como un proceso continuo, por ejemplo, s??lidos y l??quidos (es decir, los l??quidos y los gases ).
Mec??nica relativista (es decir, incluyendo los especiales y generales teor??as de la relatividad), para los ??rganos cuya velocidad cercana a la velocidad de la luz.
La mec??nica estad??stica , que proporciona un marco para relacionar las propiedades microsc??picas de los ??tomos y mol??culas individuales a los macrosc??picos o granel termodin??micas propiedades de los materiales.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Classical_mechanics&oldid=557267211 "