La relatividad general

Un simulado agujero negro de diez masas solares, visto desde una distancia de 600 kilometros con la V??a L??ctea en el fondo.

La relatividad general o la teor??a general de la relatividad es la geom??trica la teor??a de la gravitaci??n publicada por Albert Einstein en 1916. Es la descripci??n del estado de la t??cnica de la gravedad en la moderna f??sica . Unifica la relatividad especial y La ley de Newton de la gravitaci??n universal, y describe la gravedad como una propiedad de la geometr??a de espacio y tiempo, o espacio tiempo. En particular, la curvatura del espacio-tiempo est?? directamente relacionada con la cuatro impulso ( masa-energ??a y lineal impulso ) de cualquier materia y radiaci??n est??n presentes. La relaci??n se especifica por el Ecuaciones de campo de Einstein, un sistema de ecuaciones diferenciales parciales .

Las predicciones de la relatividad general difieren significativamente de los de la f??sica cl??sica, especialmente en relaci??n con el paso del tiempo, la geometr??a del espacio, el movimiento de los cuerpos en ca??da libre, y la propagaci??n de la luz . Ejemplos de tales diferencias incluyen dilataci??n gravitacional del tiempo, la corrimiento al rojo gravitacional de la luz, y la retardo de tiempo gravitacional. Predicciones de la relatividad general se han confirmado en todo observaciones y experimentos hasta la fecha. Aunque la relatividad general es no es la ??nica teor??a relativista de la gravedad, es el m??s simple tal teor??a de que es consistente con los datos experimentales. Sin embargo, quedan preguntas sin respuesta, siendo el m??s importante la forma general de la relatividad se puede reconciliar con las leyes de la f??sica cu??ntica para producir una teor??a completa y auto-consistente de la gravedad cu??ntica.

La teor??a de Einstein tiene aplicaciones astrof??sicas importantes. Se apunta hacia la existencia de agujeros negros -regiones del espacio en el que el espacio y el tiempo est??n distorsionados de tal manera que nada, ni siquiera la luz, puede escapar, como un estado final de masivas estrellas . Hay pruebas de que tales agujeros negros estelares, as?? como variedades m??s masivas de agujero negro son responsables de la intensa radiaci??n emitida por ciertos tipos de objetos astron??micos, tales como n??cleos gal??cticos activos o microcu??sares. La curvatura de la luz por la gravedad puede conducir al fen??meno de la lentes gravitacionales, donde varias im??genes del mismo objeto astron??mico distante son visibles en el cielo. La relatividad general tambi??n predice la existencia de ondas gravitacionales, que ya han sido medidos indirectamente; una medici??n directa es el objetivo de proyectos como LIGO. Adem??s, la relatividad general es la base del actual cosmol??gicos modelos de un universo en expansi??n.

La relatividad general
Introducci??n Formulaci??n matem??tica Recursos
Conceptos fundamentales La relatividad especial Principio de equivalencia Line Mundial ?? La geometr??a de Riemann
Fen??menos Problema de Kepler ?? Lentes ?? Ondas Torsi??n por arrastre ?? Efecto geod??sico Horizonte de eventos ?? Singularidad Agujero negro
Ecuaciones Gravedad linealizada Formalismo post-newtoniana Ecuaciones de campo de Einstein Ecuaci??n geod??sica Ecuaciones de Friedmann ADM formalismo BSSN formalismo Ecuaci??n de Hamilton-Jacobi-Einstein
Teor??as avanzadas Kaluza-Klein La gravedad cu??ntica
Soluciones Schwarzschild Reissner-Nordstr??m ?? G??del Kerr ?? Kerr-Newman Kasner ?? Taub-NUT ?? Milne ?? Robertson-Walker de onda pp ?? polvo van Stockum
Los cient??ficos Einstein ?? Lorentz ?? Hilbert ?? Poincar?? ?? Schwarzschild ?? Sitter ?? Reissner ?? Nordstr??m ?? Weyl ?? Eddington ?? Friedman ?? Milne ?? Zwicky ?? Lema??tre ?? G??del ?? Wheeler ?? Robertson ?? Bardeen ?? Walker ?? Kerr ?? Chandrasekhar ?? Ehlers ?? Penrose ?? Hawking ?? Taylor ?? Hulse ?? Stockum ?? Taub ?? Hombre Nuevo Yau ?? Thorne otros
Espacio Tiempo Espacio Tiempo Espaciotiempo de Minkowski Diagramas espacio-tiempo Espacio-tiempo en la relatividad general

Historia

Primera p??gina del manuscrito de Einstein para explicar la relatividad general

Poco despu??s de la publicaci??n de la teor??a especial de la relatividad en 1905, Einstein comenz?? a pensar en c??mo incorporar la gravedad en su nuevo marco relativista. En 1907, comenzando con un simple pens?? experimento con un observador en ca??da libre, se embarc?? en lo que ser??a una b??squeda de ocho a??os para una teor??a relativista de la gravedad. Despu??s de numerosos desv??os y falsos comienzos, su trabajo culmin?? con la de noviembre de 1915 a la presentaci??n Academia Prusiana de Ciencias de lo que ahora se conoce como el Ecuaciones de campo de Einstein. Estas ecuaciones especifican c??mo la geometr??a del espacio y el tiempo est?? influenciado por lo que importa es el presente y forman el n??cleo de la teor??a general de la relatividad de Einstein.

Las ecuaciones de campo de Einstein son no lineal y muy dif??cil de resolver. Einstein utiliz?? m??todos de aproximaci??n en la elaboraci??n de las predicciones iniciales de la teor??a. Pero ya en 1916, el astrof??sico Karl Schwarzschild encontr?? la primera soluci??n exacta no trivial a las ecuaciones de campo de Einstein, la denominada soluci??n de M??trica de Schwarzschild. Esta soluci??n se sentaron las bases para la descripci??n de las etapas finales del colapso gravitacional, y los objetos conocidos hoy como los agujeros negros . En el mismo a??o, los primeros pasos hacia la generalizaci??n de la soluci??n de Schwarzschild para el??ctricamente cargadas se tomaron los objetos, que finalmente dio lugar a la Soluci??n Reissner-Nordstr??m, ahora asociado con agujeros negros cargados. En 1917, Einstein aplic?? su teor??a al universo como un todo, iniciando el campo de la relativista cosmolog??a . En l??nea con el pensamiento contempor??neo, que asumi?? un universo est??tico, a??adiendo un nuevo par??metro en sus ecuaciones de campo originales -la constante cosmol??gica a reproducir esa "observaci??n". Para 1929, sin embargo, el trabajo de Hubble y otros hab??an demostrado que nuestro universo se est?? expandiendo. Esto se describe f??cilmente por las soluciones cosmol??gicas expansi??n encontrados por Friedmann en 1922, que no requieren de una constante cosmol??gica. Lema??tre utilizar estas soluciones para formular la primera versi??n de los grandes de la explosi??n modelos, en los que nuestro universo ha evolucionado a partir de un estado anterior extremadamente caliente y denso. Einstein m??s tarde declar?? que la constante cosmol??gica el mayor error de su vida.

Durante ese per??odo, la relatividad general se mantuvo en una especie de curiosidad entre las teor??as f??sicas. Era claramente superior a La gravedad newtoniana, siendo consistente con la relatividad especial y la contabilidad de varios efectos no explicados por la teor??a newtoniana. El mismo Einstein hab??a demostrado en 1915 c??mo su teor??a explica la an??mala avance del perihelio del planeta Mercurio sin par??metros arbitrarios ("factores de dulce de az??car"). Del mismo modo, una expedici??n de 1919 dirigido por Eddington confirm?? la predicci??n de la relatividad general para la desviaci??n de la luz estelar por el Sol, por lo que Einstein inmediatamente famoso. Sin embargo, la teor??a entr?? en la corriente principal de la la f??sica te??rica y la astrof??sica s??lo con los acontecimientos ocurridos entre aproximadamente 1960 y 1975, ahora conocido como el Edad de oro de la relatividad general. Los f??sicos comenzaron a entender el concepto de un agujero negro , y para identificar manifestaci??n astrof??sico de estos objetos como cu??sares. Pruebas del sistema solar cada vez m??s precisas confirmaron poder predictivo de la teor??a, y la cosmolog??a relativista, tambi??n, se convirti?? en susceptible de dirigir las pruebas observacionales.

De la mec??nica cl??sica a la relatividad general

La relatividad general se entiende mejor mediante el examen de sus similitudes con y salidas desde la f??sica cl??sica. El primer paso es la comprensi??n de que la mec??nica cl??sica y la ley de gravedad de Newton admiten una descripci??n geom??trica. La combinaci??n de esta descripci??n con las leyes de los resultados de la relatividad especial en una derivaci??n heur??stica de la relatividad general.

Geometr??a de la gravedad de Newton

En la base de la mec??nica cl??sica es la noci??n de que un el movimiento del cuerpo puede ser descrito como una combinaci??n de libre (o inercial) movimiento, y las desviaciones de este movimiento libre. Estas desviaciones son causadas por fuerzas externas que act??an sobre un cuerpo, de acuerdo con el segundo de Newton ley del movimiento , que establece que la fuerza que act??a sobre un cuerpo es igual a (inercial) de ese cuerpo de masa veces su aceleraci??n . Los movimientos de inercia preferidos est??n relacionados con la geometr??a de el espacio y el tiempo : en la norma marcos de referencia de la mec??nica cl??sica, los objetos en movimiento libre se mueven a lo largo de l??neas rectas a velocidad constante. En lenguaje moderno, sus caminos son geod??sicas, recto l??neas mundiales en espacio tiempo.

Bola que cae al suelo en un cohete acelerado (izquierda), y en la Tierra (a la derecha)

Por el contrario, se podr??a esperar que los movimientos de inercia, una vez identificados mediante la observaci??n de los movimientos reales de los cuerpos y hacer provisiones para las fuerzas externas (como el electromagnetismo o fricci??n), se puede utilizar para definir la geometr??a del espacio, as?? como un tiempo de de coordenadas. Sin embargo, hay una ambig??edad una vez la gravedad entra en juego. De acuerdo a Ley de la gravedad de Newton, y verificada independientemente por los experimentos como el de E??tv??s y sus sucesores (ver E??tv??s experimento), hay una universalidad de ca??da libre (tambi??n conocido como el d??bil principio de equivalencia, o la igualdad universal de la masa inercial y pasivo-gravitacional): la trayectoria de un cuerpo de prueba en ca??da libre s??lo depende de su posici??n y la velocidad inicial, pero no en cualquiera de sus propiedades del material. Una versi??n simplificada de este se materializa en el experimento del ascensor de Einstein, que se ilustra en la figura de la derecha: para un observador en una peque??a habitaci??n cerrada, es imposible decidir, mediante la asignaci??n de la trayectoria de los cuerpos, como un bal??n a tierra, si la habitaci??n est?? en reposo en un campo gravitatorio, o en el espacio libre de a bordo de un cohete acelerado.

Dada la universalidad de ca??da libre, no hay distinci??n entre observable movimiento inercial y el movimiento bajo la influencia de la fuerza gravitacional. Esto sugiere la definici??n de una nueva clase de movimiento inercial, es decir, que los objetos en ca??da libre bajo la influencia de la gravedad. Esta nueva clase de movimientos preferidos, tambi??n, define una geometr??a del espacio y el tiempo en t??rminos matem??ticos, es el movimiento geod??sico asociado con una espec??fica conexi??n que depende de la gradiente de la potencial gravitacional. El espacio, en esta construcci??n, todav??a tiene la ordinaria geometr??a euclidiana . Sin embargo, el espacio tiempo como un todo es m??s complicado. Como se muestra, utilizando simples pensado experimentos siguiendo las trayectorias de ca??da libre de las diferentes part??culas de prueba, el resultado del transporte de vectores del espacio-tiempo que puede denotar la velocidad de una part??cula (vectores de tiempo similar) variar?? con la trayectoria de la part??cula; matem??ticamente hablando, la conexi??n de Newton no es integrable. A partir de esto, se puede deducir que el espacio-tiempo es curvo . El resultado es una formulaci??n geom??trica de la gravedad newtoniana utilizando s??lo conceptos covariantes, es decir, una descripci??n que es v??lida en cualquier sistema de coordenadas deseado. En esta descripci??n geom??trica, en efectos de la marea aceleraci??n relativa de los cuerpos en ca??da libre-est??n relacionados con la derivada de la conexi??n, que muestra c??mo la geometr??a modificada es causada por la presencia de la masa.

Generalizaci??n relativista

Cono de luz

Tan intrigante como geom??trico gravedad newtoniana puede ser, su base, la mec??nica cl??sica, no es m??s que un caso l??mite de relativistas (especiales) la mec??nica. En el lenguaje de la simetr??a : donde la gravedad puede ser descuidado, la f??sica es Lorentz invariante como en la relatividad especial en lugar de Galilei invariante como en la mec??nica cl??sica. (La simetr??a definici??n de la relatividad especial es el Grupo de Poincar??, que tambi??n incluye traducciones y rotaciones.) Las diferencias entre los dos se vuelven significativas cuando se trata de velocidades cercanas a la velocidad de la luz , y con los fen??menos de alta energ??a.

Con la simetr??a de Lorentz, estructuras adicionales entra en juego. Se definen por el conjunto de los conos de luz (ver la imagen de la izquierda). Los conos de luz definen una estructura causal: para cada evento A, hay un conjunto de eventos que puede, en principio, bien influir o ser influidos por A trav??s de se??ales o interacciones que no necesitan viajar m??s r??pido que la luz (como evento B en la imagen), y un conjunto de eventos para los que tal influencia no es posible (como evento C en la imagen). Estos conjuntos son independientes del observador. En conjunci??n con el mundo l??neas de part??culas en ca??da libre, los conos de luz pueden ser usados para reconstruir m??trica semi-riemanniana del espacio-tiempo, al menos hasta un factor escalar positivo. En t??rminos matem??ticos, esto define una estructura conformal.

La relatividad especial se define en la ausencia de gravedad, por lo que para las aplicaciones pr??cticas, es un modelo adecuado siempre que la gravedad puede ser descuidado. Traer gravedad en juego, y asumiendo la universalidad de la ca??da libre, un razonamiento an??logo al igual que en el apartado anterior se aplica: no hay mundial sistemas inerciales. En cambio, hay marcos inerciales aproximadas m??viles part??culas junto con la ca??da libre. Traducido al lenguaje del espacio-tiempo: la recta l??neas de tiempo similar que definen un marco inercial libre de gravedad se deforman a las l??neas que se curvan uno respecto al otro, lo que sugiere que la inclusi??n de gravedad requiere un cambio en la geometr??a espacio-tiempo.

A priori, no est?? claro si los nuevos marcos locales en ca??da libre coincidir con los marcos de referencia en el que las leyes de la relatividad especial de sujeci??n que la teor??a se basa en la propagaci??n de la luz, y por lo tanto en el electromagnetismo , que podr??a tener un conjunto diferente de marcos preferido. Pero el uso de diferentes supuestos sobre los marcos especiales relativista (como su ser tierra-fijo, o en ca??da libre), se puede derivar diferentes predicciones para el corrimiento al rojo gravitacional, es decir, la forma en que la frecuencia de la luz cambia como la luz se propaga a trav??s de un campo gravitatorio (cf. m??s adelante ). Las mediciones reales muestran que los marcos en ca??da libre son aquellos en los que la luz se propaga como lo hace en la relatividad especial. La generalizaci??n de esta declaraci??n, a saber, que las leyes de la relatividad especial espera a buena aproximaci??n en ca??da libre (y no rotativo) marcos de referencia, que se conoce como el Einstein principio de equivalencia, un principio rector fundamental para la generalizaci??n de la f??sica relativista especiales para incluir la gravedad.

Los mismos datos experimentales muestran que el tiempo medido por los relojes en un campo gravitacional el momento adecuado, para dar el t??rmino no-t??cnico no seguir las reglas de la relatividad especial. En el lenguaje de la geometr??a del espacio-tiempo, no se mide por el M??trica de Minkowski. Como en el caso newtoniano, esto es sugerente de una geometr??a m??s general. A peque??a escala, todos los marcos de referencia que est??n en ca??da libre son equivalentes, y aproximadamente Minkowski. En consecuencia, ahora estamos tratando con una generalizaci??n curvada del espacio de Minkowski. La tensor m??trico que define la geometr??a, en particular, c??mo se longitudes y ??ngulos no miden-es la m??trica de Minkowski de la relatividad especial, es una generalizaci??n conocida como semi o pseudo-riemanniana m??trica. Adem??s, cada m??trica de Riemann se asocia naturalmente con un tipo particular de conexi??n, el Conexi??n de Levi-Civita, y este es, de hecho, la conexi??n que satisface el principio de equivalencia y hace espacio localmente minkowskiana (es decir, en coordenadas adecuadas "localmente inerciales", la m??trica de Minkowski es, y sus derivados y los coeficientes de conexi??n desaparecen) .

Las ecuaciones de Einstein

Despu??s de haber formulado la versi??n relativista, geom??trica de los efectos de la gravedad, la cuesti??n de la fuente de gravedad permanece. En la gravedad newtoniana, la fuente es la masa. En la relatividad especial, la masa resulta ser parte de una cantidad m??s general llamado tensor energ??a-impulso, que incluye tanto energ??a y momentum densidades as?? como estr??s (es decir, presi??n y cizallamiento). Utilizando el principio de equivalencia, este tensor se generaliza f??cilmente a espacio-tiempo curvo. Dibujo adem??s a la analog??a con la gravedad newtoniana geom??trica, es natural suponer que la ecuaci??n de campo de gravedad se relaciona este tensor y la Tensor de Ricci, que describe una clase particular de efectos de marea: el cambio de volumen para una peque??a nube de part??culas de prueba que son inicialmente en reposo, y luego caen libremente. En la relatividad especial, conservaci??n de la energ??a-impulso corresponde a la afirmaci??n de que el tensor de energ??a-momento es -divergencia libre. Esta f??rmula tambi??n se generaliza f??cilmente para curvado espacio-tiempo mediante la sustituci??n de las derivadas parciales con sus hom??logos de curvas colector, derivadas covariantes. Con esta condici??n, la divergencia covariante adicional del tensor de energ??a-momento, y por lo tanto de lo que est?? en el otro lado de la ecuaci??n, es cero el conjunto m??s simple de las ecuaciones son lo que se llama (de campo) las ecuaciones de Einstein:

En el lado de la izquierda es una combinaci??n espec??fica-divergencia libre de la Tensor de Ricci y la m??trica conocida como la Tensor de Einstein. En particular,

es el escalar de curvatura. El propio tensor de Ricci est?? relacionada con el tensor de curvatura de Riemann m??s general como

En el lado derecho, T _ab es el tensor de energ??a-impulso. Todos los tensores est??n escritos en notaci??n ??ndice abstracto. Coincidencia de la predicci??n de la teor??a a resultados observacionales para planetaria ??rbitas (o, equivalentemente, asegurando que la d??bil gravedad, l??mite de baja velocidad es la mec??nica de Newton), la constante de proporcionalidad se pueden fijar como κ = 8π G / c ^4, con la G constante gravitacional y c la velocidad de la luz . Cuando no hay materia presente, por lo que el tensor de energ??a-momento se desvanece, el resultado es el vac??o ecuaciones de Einstein,

Hay alternativas a la relatividad general construida sobre las mismas instalaciones, que incluyen normas y / o restricciones adicionales, que conducen a diferentes ecuaciones de campo. Ejemplos son Teor??a de Brans-Dicke, Teleparalelismo, y La teor??a de Einstein-Cartan.

Definici??n y aplicaciones b??sicas

La derivaci??n se indica en la secci??n anterior contiene toda la informaci??n necesaria para definir la relatividad general, describir sus propiedades clave, y abordar una cuesti??n de importancia crucial en la f??sica, es decir, c??mo la teor??a puede ser utilizado para la construcci??n de modelos.

Definici??n y propiedades b??sicas

La relatividad general es una teor??a m??trica de la gravitaci??n . En su parte central se encuentran Las ecuaciones de Einstein, que describen la relaci??n entre la geometr??a de cuatro dimensiones, semi- Riemann colector que representa espacio-tiempo, por una parte, y la energ??a-impulso contenida en el espacio-tiempo que en el otro. Fen??menos que en la mec??nica cl??sica se atribuyen a la acci??n de la fuerza de gravedad (tales como caida libre, movimiento orbital, y astronave trayectorias), corresponden a movimiento inercial dentro de una geometr??a curva del espacio-tiempo en la relatividad general; no hay fuerza gravitacional desviar objetos de sus caminos rectos, naturales. En su lugar, la gravedad corresponde a los cambios en las propiedades del espacio y el tiempo, que a su vez modifica los caminos-rectas posible que los objetos seguir?? naturalmente. La curvatura est??, a su vez, causada por la energ??a-impulso de la materia. Parafraseando el relativista John Archibald Wheeler, el espacio-tiempo le dice a la materia c??mo moverse; la materia le dice el espacio-tiempo c??mo curvarse.

Mientras que la relatividad general sustituye a la potencial gravitacional escalar de la f??sica cl??sica por un sim??trico rango de dos tensor, este ??ltimo se reduce a la antigua, en cierta casos l??mite. Para campos gravitatorios d??biles y velocidad lenta con respecto a la velocidad de la luz, las predicciones de la teor??a convergen en los de La ley de Newton de la gravedad.

Como se construye utilizando tensores, exhibiciones de la relatividad general covariancia general: sus leyes-y otras leyes formuladas en el marco de la relatividad general-toma en la misma forma en todos los sistemas de coordenadas. Adem??s, la teor??a no contiene ning??n geom??tricas estructuras de fondo invariables. Por lo tanto, satisface una m??s estricta principio general de la relatividad, a saber, que la leyes de la f??sica son las mismas para todos los observadores. Localmente, tal como se expresa en el principio de equivalencia, el espacio-tiempo es Minkowski, y las leyes de la f??sica de exposiciones invariancia Lorentz local.

El fomento de Modelo

El concepto central de la construcci??n de modelos-relativistas es el de un soluci??n de las ecuaciones de Einstein. Teniendo en cuenta tanto las ecuaciones de Einstein y las ecuaciones adecuadas para las propiedades de la materia, una soluci??n de este tipo consiste en un colector espec??fico semi-Riemann (generalmente definida por dar la m??trica en coordenadas espec??ficas), y campos de materia espec??ficos definidos en dicha colector. La materia y la geometr??a deben satisfacer las ecuaciones de Einstein, por lo que, en particular, la energ??a-impulso tensor de la materia deben ser divergencia libre. El asunto debe, por supuesto, tambi??n satisfacer wheatever se impusieron ecuaciones adicionales en sus propiedades. En definitiva, una soluci??n de este tipo es un modelo de universo que satisfaga a las leyes de la relatividad general, y las leyes posiblemente adicionales que regulan cualquier asunto pudiera estar presente.

Las ecuaciones de Einstein son no lineales de ecuaciones diferenciales parciales y, como tal, dif??cil de resolver con exactitud. Sin embargo, un n??mero de soluciones exactas son conocidas, aunque s??lo unos pocos tienen aplicaciones f??sicas directas. Las soluciones exactas m??s conocidos, y tambi??n los m??s interesantes desde el punto de vista de la f??sica, son los Soluci??n de Schwarzschild, la Soluci??n Reissner-Nordstr??m y la Kerr m??trico, cada uno correspondiente a un determinado tipo de agujero negro en un universo por lo dem??s vac??o, y el Friedmann-Lema??tre-Robertson-Walker y universos de Sitter, cada uno describiendo un cosmos en expansi??n. Soluciones exactas de gran inter??s te??rico incluyen la G??del universo (que abre la posibilidad intrigante de viaje en el tiempo en espacio-tiempos curvos), la Soluci??n Taub-NUT (un modelo de universo que es homog??nea, pero anisotr??pico), y Espacio anti-de Sitter (que ha llegado recientemente a la prominencia en el contexto de lo que se llama la Maldacena conjetura).

Dada la dificultad de encontrar soluciones exactas, las ecuaciones de campo de Einstein tambi??n se resuelven con frecuencia por la integraci??n num??rica en un ordenador, o bien considerando las peque??as perturbaciones de las soluciones exactas. En el campo de relatividad num??rica, se emplean potentes ordenadores para simular la geometr??a del espacio-tiempo y para resolver las ecuaciones de Einstein para situaciones interesantes, como colisi??n de dos agujeros negros . En principio, estos m??todos pueden ser aplicados a cualquier sistema, dados los recursos inform??ticos suficientes, y pueden abordar cuestiones fundamentales como singularidades desnudas. Soluciones aproximadas tambi??n pueden ser encontrados teor??as de perturbaci??n tales como la gravedad linealizado y su generalizaci??n, la expansi??n post-newtoniana, los cuales fueron desarrollados por Einstein. Esta ??ltima ofrece un enfoque sistem??tico para la soluci??n de la geometr??a de un espacio-tiempo que contiene una distribuci??n de la materia que se mueve lentamente en comparaci??n con la velocidad de la luz. La expansi??n implica una serie de t??rminos; los primeros t??rminos representan la gravedad newtoniana, mientras que los t??rminos posteriores representan correcciones cada vez m??s peque??os a la teor??a de Newton debido a la relatividad general. Una extensi??n de esta expansi??n es la post-newtoniana (PPN) formalismo parametrizada, lo que permite hacer comparaciones cuantitativas entre las predicciones de la relatividad general y teor??as alternativas.

Consecuencias de la teor??a de Einstein

La relatividad general tiene una serie de consecuencias f??sicas. Algunos siguen directamente de los axiomas de la teor??a, mientras que otros han puesto de manifiesto s??lo en el transcurso de los noventa a??os de investigaciones que siguieron a la publicaci??n inicial de Einstein.

La dilataci??n del tiempo gravitacional y desplazamiento de frecuencia

Representaci??n esquem??tica de la corrimiento al rojo gravitacional de una onda de luz que escapa de la superficie de un cuerpo masivo

Suponiendo que el principio de equivalencia se mantiene, la gravedad influye en el paso del tiempo. Luz enviada abajo en un as?? gravedad es blueshifted, mientras que la luz enviada en la direcci??n opuesta (es decir, saliendo del pozo de gravedad) es desplazada hacia el rojo ; En conjunto, estos dos efectos se conocen como el desplazamiento de frecuencia gravitacional. De manera m??s general, los procesos de cierre a una corrida enorme cuerpo m??s lentamente en comparaci??n con los procesos que tienen lugar m??s lejos; Este efecto se conoce como la dilataci??n del tiempo gravitacional.

Corrimiento al rojo gravitacional se ha medido en el laboratorio y el uso de las observaciones astron??micas. La dilataci??n del tiempo gravitacional en el campo gravitacional de la Tierra se ha medido varias veces usando relojes at??micos, mientras que la validaci??n en curso se proporciona como un efecto secundario de la operaci??n de la Sistema de Posicionamiento Global (GPS). Las pruebas en campos gravitacionales fuertes son proporcionados por la observaci??n de p??lsares binarios. Todos los resultados est??n de acuerdo con la relatividad general. Sin embargo, en el nivel actual de la precisi??n, estas observaciones no pueden distinguir entre la relatividad general y otras teor??as en las que el principio de equivalencia es v??lida.

Desviaci??n de la luz y retardo de tiempo gravitacional

Desviaci??n de la luz (enviado desde la ubicaci??n que se muestra en azul) cerca de una masa compacta (en gris)

La relatividad general predice que el camino de la luz se curva en un campo gravitatorio; luz que pasa a un cuerpo masivo es desviado hacia ese cuerpo. Este efecto ha sido confirmado por la observaci??n de la luz de las estrellas o distante cu??sares siendo desviados a medida que pasa el Sol .

Esto y predicciones relacionadas deduce del hecho de que la luz sigue lo que se llama una luz similar o nula geod??sica una generalizaci??n de las l??neas rectas a lo largo de la cual la luz viaja en la f??sica cl??sica. Tales geod??sicas son la generalizaci??n de la invariancia de velocidad de la luz en la relatividad especial . Como uno examina espaciotiempos modelo adecuados (ya sea en el exterior Soluci??n de Schwarzschild o, por m??s de una sola masa, la expansi??n post-newtoniana), varios efectos de la gravedad sobre la propagaci??n de la luz emergen. Aunque la curvatura de la luz tambi??n se puede derivar mediante la ampliaci??n de la universalidad de la ca??da libre de la luz , el ??ngulo de desviaci??n que resulta de estos c??lculos es s??lo la mitad del valor dado por la relatividad general.

En estrecha relaci??n con desviaci??n de la luz es el retraso gravitacional tiempo (o efecto Shapiro), el fen??meno de que las se??ales de luz tardan m??s en pasar a trav??s de un campo gravitatorio que lo har??an en ausencia de ese campo. Ha habido numerosas pruebas exitosas de esta predicci??n. En el parametrizada formalismo post-newtoniana (PPN), las mediciones tanto de la desviaci??n de la luz y el tiempo de retardo gravitacional determinar un par??metro llamado 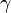, Que codifica la influencia de la gravedad en la geometr??a del espacio.

Las ondas gravitacionales

Anillo de part??culas de prueba flotando en el espacio

Anillo de prueba de part??culas influenciada por ondas gravitacionales

Una de las varias analog??as entre la gravedad de campo d??bil y el electromagnetismo es que, de forma an??loga a las ondas electromagn??ticas , hay ondas gravitacionales: ondas en la m??trica del espacio-tiempo que se propagan en la velocidad de la luz . El tipo m??s simple de una onda de este tipo puede ser visualizado por su acci??n sobre un anillo de part??culas libremente flotantes (imagen superior a la derecha). Una onda sinusoidal se propaga a trav??s de un anillo como hacia el lector distorsiona el anillo en una caracter??stica, de forma r??tmica (bajo, imagen animada a la derecha). Desde las ecuaciones de Einstein son no lineal, de manera arbitraria fuertes ondas gravitacionales no obedecen superposici??n lineal, por lo que su descripci??n dif??cil. Sin embargo, para los campos d??biles, una aproximaci??n lineal se puede hacer. Estas ondas gravitacionales linealizadas son suficientemente precisos para describir las olas extremadamente d??biles que se esperan para llegar aqu?? en la Tierra de los acontecimientos c??smicos lejanos, que normalmente resultan en distancias relativas aumentando y disminuyendo por o menos. M??todos de an??lisis de datos rutinariamente hacen uso del hecho de que estas ondas pueden ser linealizadas Fourier descompone.

Algunos soluciones exactas describen ondas gravitacionales sin ninguna aproximaci??n, por ejemplo, un tren de onda que viaja a trav??s del espacio vac??o o la llamada Universos Gowdy, variedades de un cosmos en expansi??n llenas de ondas gravitacionales. Pero para las ondas gravitacionales producidas en situaciones astrof??sicamente pertinentes, como la fusi??n de dos agujeros negros, m??todos num??ricos son actualmente la ??nica manera de construir modelos apropiados.

Efectos orbitales y la relatividad de la direcci??n

La relatividad general se diferencia de la mec??nica cl??sica en una serie de predicciones sobre los cuerpos que orbitan. Se predice una rotaci??n general ( precesi??n) de las ??rbitas planetarias, as?? como la degradaci??n orbital causado por la emisi??n de ondas gravitacionales y los efectos relacionados con la relatividad de la direcci??n.

Precesi??n de ??psides

Newtoniano (rojo) vs. ??rbita de Einstein (azul) de un planeta orbitando una estrella solitaria

En la relatividad general, la ??psides de cualquier ??rbita (el punto m??s cercano de aproximaci??n del cuerpo que orbita al del sistema centro de masas ) se precesi??n-la ??rbita no es una elipse , pero similar a una elipse que gira sobre su enfoque, resultando en una rosa-curva como forma (ver imagen). Einstein deriva primero este resultado mediante el uso de una m??trica aproximado que representa el l??mite newtoniano y el tratamiento del cuerpo en ??rbita como part??cula de prueba. Para ??l, el hecho de que su teor??a dio una explicaci??n directa de la desplazamiento del perihelio an??malo del planeta Mercurio , descubierto anteriormente por Urbain Le Verrier en 1859, fue una importante evidencia de que hab??a identificado al fin la forma correcta del ecuaciones del campo gravitatorio.

El efecto tambi??n se puede derivar mediante el uso de ya sea la exacta M??trica de Schwarzschild (que describe el espacio-tiempo alrededor de una masa esf??rica) o la mucho m??s general formalismo post-newtoniana. Es debido a la influencia de la gravedad en la geometr??a del espacio y a la contribuci??n de auto-energ??a a la gravedad de un cuerpo (codificada en el no linealidad de las ecuaciones de Einstein). Precesi??n relativista se ha observado en todos los planetas que permiten mediciones precisas de precesi??n (Mercurio, Venus y la Tierra ), as?? como en sistemas de pulsares binarios, en los que es m??s grande por cinco ??rdenes de magnitud.

Decaimiento orbital

Decaimiento orbital para PSR1913 + 16: cambio de tiempo en segundos, seguido m??s de tres d??cadas.

De acuerdo con la relatividad general, una sistema binario emitir?? ondas gravitacionales, perdiendo as?? la energ??a . Debido a esta p??rdida, la distancia entre los dos cuerpos que orbitan disminuye, y tambi??n lo hace su periodo orbital. Dentro del sistema solar o de corriente estrellas dobles, el efecto es demasiado peque??o para ser observable. No as?? para su fin pulsar binario, un sistema de dos en ??rbita las estrellas de neutrones, uno de los cuales es un p??lsar: desde el p??lsar, los observadores de la Tierra reciben una serie regular de pulsos de radio que pueden servir como un reloj de alta precisi??n, lo que permite realizar mediciones precisas del periodo orbital. Dado que las estrellas de neutrones son muy compactos, cantidades significativas de energ??a se emiten en forma de radiaci??n gravitatoria.

La primera observaci??n de una disminuci??n en el periodo orbital debido a la emisi??n de las ondas gravitacionales fue hecha por Hulse y Taylor, utilizando el p??lsar binario PSR1913 + 16 que hab??an descubierto en 1974. Esta fue la primera detecci??n de ondas gravitacionales, aunque indirecto, para el que fueron galardonados con el 1993 Premio Nobel de F??sica. Desde entonces, se han encontrado varios otros p??lsares binarios, en particular la doble pulsar PSR J0737-3039, en el que ambas estrellas son p??lsares.

Precesi??n geod??sica y arrastre de marco

Varios efectos relativistas est??n directamente relacionados con la relatividad de la direcci??n. Uno es precesi??n geod??sica: la direcci??n del eje de una giroscopio en ca??da libre en espacio-tiempo curvado va a cambiar cuando se compara, por ejemplo, con la direcci??n de la luz recibida de estrellas lejanas, incluso aunque un giroscopio como representa la forma de mantener una direcci??n lo m??s estable posible (" transporte paralelo ") Para el. Luna - Tierra -system, este efecto se ha medido con la ayuda de medici??n l??ser lunar. M??s recientemente, se ha medido para masas de prueba a bordo del sat??lite Gravity Probe B con una precisi??n superior a 1 por ciento.

Cerca de una masa en rotaci??n, no son los llamados gravitomagn??tico o torsi??n por arrastre efectos. Un observador distante determinar?? que los objetos cerca de los medios de conseguir "arrastrado alrededor". Esto es m??s extrema para agujeros negros en rotaci??n en el que, para cualquier objeto de entrar en una zona conocida como la ergosfera, la rotaci??n es inevitable. Tales efectos pueden ser probadas de nuevo a trav??s de su influencia en la orientaci??n de los giroscopios en ca??da libre. Pruebas un tanto controversiales se han realizado utilizando el Sat??lites LAGEOS, confirmando la predicci??n relativista. Una medici??n de precisi??n es el objetivo principal de la Misi??n Gravity Probe B, con los resultados que se esperan de septiembre de 2008.

Aplicaciones Astrophysical

La lente gravitatoria

Einstein cruz: cuatro im??genes del mismo objeto astron??mico, producidos por una lente gravitacional

La desviaci??n de la luz por la gravedad es responsable de una nueva clase de fen??menos astron??micos. Si un objeto masivo est?? situado entre el astr??nomo y un objeto de destino distante con distancias de masas y relativas apropiadas, el astr??nomo ver?? m??ltiples im??genes distorsionadas de la meta. Tales efectos se conocen como lente gravitacional. Dependiendo de la configuraci??n, la escala y distribuci??n de la masa, no puede haber dos o m??s im??genes, un anillo brillante conocido como Anillo de Einstein, o anillos parciales llamados arcos. La ejemplo m??s temprano fue descubierto en 1979; desde entonces, se han observado más de un centenar de lentes gravitacionales. Incluso si están demasiado cerca uno del otro a resolver las múltiples imágenes, el efecto aún se puede medir, por ejemplo, como un brillo total del objeto de destino; una serie de tales " se ha observado eventos de microlente ".

La lente gravitatoria se ha convertido en una herramienta de la astronomía observacional. Se utiliza para detectar la presencia y distribución de la materia oscura , proporcionar un "telescopio natural" para la observación de galaxias distantes, y para obtener una estimación independiente de la constante de Hubble . Las evaluaciones estadísticas de datos de lentes proporcionan información valiosa sobre la evolución estructural de las galaxias .

La astronomía de ondas gravitacionales

Impresión del detector de ondas gravitacionales espacio transmitidas del artistaLISA

Las observaciones de pulsares binarios proporcionan una fuerte evidencia indirecta de la existencia de las ondas gravitacionales (véase el decaimiento orbital , arriba). Sin embargo, las ondas gravitacionales que nos llegan desde las profundidades del cosmos no se han detectado directamente, que es un objetivo importante de la investigación relacionada con la relatividad de corriente. Varios terrestres detectores de ondas gravitacionales están actualmente en operación, más notablemente los detectores interferométricos GEO 600, LIGO (tres detectores), TAMA 300 y VIRGO. Un detector espacial estadounidense-europeo conjunto, LISA, se encuentra actualmente en fase de desarrollo, con una misión precursora ( LISA Pathfinder) que se lanzará a finales de 2009.

Las observaciones de las ondas gravitacionales prometen para complementar las observaciones en el espectro electromagn??tico.Se espera que proporcionar información sobre los agujeros negros y otros objetos densos, como las estrellas de neutrones y las enanas blancas, sobre ciertos tipos desupernovasimplosiones, y sobre los procesos en el universo muy temprano, incluyendo la firma de ciertos tipos de hipotéticacuerda cósmica.

Los agujeros negros y otros objetos compactos

Simulación basado en las ecuaciones de la relatividad general: una estrella que colapsa para formar un agujero negro, mientras que la emisión de ondas gravitacionales

Siempre que un objeto se convierte en lo suficientemente compacta, la relatividad general predice la formación de un agujero negro , una región del espacio de la cual nada, ni siquiera la luz, puede escapar. En los modelos actualmente aceptados de la evolución estelar, estrellas de neutrones con alrededor de 1,4 masas solares y los llamados agujeros negros estelares con unos pocos a unas pocas docenas se piensa masas solares para ser el estado final de la evolución de las estrellas masivas. Los agujeros negros supermasivos con unos cuantos millones a unos mil millones de masas solares se consideran la regla y no la excepción en los centros de las galaxias, y su presencia se cree que han desempeñado un papel importante en la formación de galaxias y estructuras cósmicas más grandes.

Astronómicamente, la propiedad más importante de objetos compactos es que proporcionan un mecanismo magníficamente eficiente para convertir la energía gravitacional en radiación electromagnética. acreción, la caída de polvo o materia gaseosa en estelares o agujeros negros supermasivos, se cree que es responsable de algunos espectacularmente luminosa objetos astronómicos, en particular diversos tipos de núcleos activos de galaxias en escalas galácticas y objetos de tamaño estelar como microcu??sares. En particular, la acreción pueden conducir a chorros relativistas, centrado haces de partículas altamente energéticas que están siendo arrojadas al espacio a casi la velocidad de la luz . La relatividad general juega un papel central en el modelado de todos estos fenómenos, y las observaciones proporcionan una fuerte evidencia de la existencia de agujeros negros con las propiedades predichas por la teoría.

Los agujeros negros también son codiciados objetivos en la búsqueda de ondas gravitacionales (cf. ondas gravitatorias , arriba). La fusión de los binarios de agujeros negros deben dar lugar a algunos de los más fuertes señales de ondas gravitacionales que alcanzan los detectores aquí en la Tierra, y la fase inmediatamente antes de la fusión ("chirrido") podría ser utilizado como una " candela estándar "para deducir la distancia a la eventos- fusión y por lo tanto servir como una sonda de la expansión cósmica a grandes distancias. Las ondas gravitacionales producidas como estelares hunde agujero negro supermasivo en uno deben proporcionar información directa sobre la geometría del agujero negro supermasivo.

Cosmolog??a

Imagen de la radiación emitida no más de unos pocos cientos de mil años después del Big Bang, capturado con el telescopio satéliteWMAP

Los modelos actuales de la cosmología se basan en las ecuaciones de Einstein, incluyendo?? constante cosmológica, que tiene influencia importante en la dinámica a gran escala del cosmos,

donde g _ab es la espacio-tiempo métrico. Isotrópico y soluciones homogéneas de estas ecuaciones mejoradas, las soluciones de Friedmann-Lemaître-Robertson-Walker, permiten a los físicos para modelar un universo que se ha desarrollado durante los últimos 14 millones de años a partir de una temprana caliente Big Bang fase. Una vez que un pequeño número de parámetros (por ejemplo media del universo la materia de densidad ) se han fijado por la observación astronómica, más datos observacionales se puede utilizar para poner los modelos a prueba. Las predicciones, todo un éxito, incluyen la abundancia inicial de elementos químicos formados en un período de nucleosíntesis primordial, la estructura a gran escala del universo, y la existencia y propiedades de un " eco térmica "de la década de cosmos, el la radiaci??n c??smica de fondo.

Observaciones astronómicas de la tasa de expansión cosmológica permiten la cantidad total de materia en el universo a estimar, aunque la naturaleza de esa materia sigue siendo un misterio, en parte. Alrededor del 90 por ciento de toda la materia parece ser la llamada materia oscura , que tiene masa (o, equivalentemente, la influencia de la gravedad), pero no interactúa electromagnéticamente y, por lo tanto, no se puede observar directamente. ¡No hay generalmente descripción de este nuevo tipo de materia aceptada, en el marco de conocida la física de partículas o de otro modo. Evidencia observacional de las encuestas de corrimiento al rojo lejano supernovas y las mediciones de la radiación cósmica de fondo también muestran que la evolución de nuestro universo está influenciada significativamente por una constante cosmológica que resulta en una aceleración de la expansión cósmica o, equivalentemente, por una forma de energía con una inusual ecuación de estado, conocida como energía oscura, la naturaleza de la cual sigue siendo poco clara.

Una llamada fase inflacionaria , una fase adicional de la expansión acelerada fuertemente en momentos cósmicos de alrededor de segundos, se planteó la hipótesis en 1980 para tener en cuenta varias observaciones desconcertantes que fueron inexplicable por los modelos cosmológicos clásicos, como la homogeneidad casi perfecta de la radiación cósmica de fondo . Mediciones recientes de la radiación cósmica de fondo han dado lugar a la primera evidencia de este escenario. Sin embargo, hay una desconcertante variedad de posibles escenarios inflacionarios, que no puede ser no restringidos por las observaciones actuales. Una pregunta aún más grande es la física del universo temprano, antes de la fase inflacionaria y cerca de donde los modelos clásicos predicen el big bang singularidad. Una respuesta autorizada requeriría una teoría completa de la gravedad cuántica, que aún no se ha desarrollado (véase la sección sobre la gravedad cuántica , más adelante).

Conceptos avanzados

Estructura causal y la geometría mundial

Diagrama de Penrose de un infinitouniverso de Minkowski

En la relatividad general, ningún cuerpo material puede ponerse al día con o adelantar a un pulso de luz. Sin la influencia de un evento A puede llegar a cualquier otro lugar X antes de la luz enviada en A para X. En consecuencia, una exploración de todas líneas de universo de luz ( geodésicas nulas) da información clave acerca de la estructura causal del espacio-tiempo. Esta estructura se puede visualizar utilizando diagramas de Penrose-Carter en la que se encogen infinitamente grandes regiones de intervalos de tiempo y espacio infinito (" compactificada ") a fin de que quepan en un mapa finito, mientras que la luz sigue viajando a lo largo de las diagonales como en estándar diagramas espacio-tiempo.

Consciente de la importancia de la estructura causal, Roger Penrose y otros desarrollaron lo que se conoce como geometría global. En geometría global, el objeto de estudio no es un particular solución (o familia de soluciones) a las ecuaciones de Einstein. Más bien, las relaciones que mantienen cierto para todas las geodésicas, como la ecuación Raychaudhuri, y los supuestos no específicos adicionales sobre la naturaleza de la materia (por lo general en forma de las llamadas condiciones de energía) se utilizan para derivar resultados generales.

Horizons

El uso de la geometría global, algunas espacio-tiempos se pueden mostrar para contener límites llamados horizontes, que delimitan una región del resto de espacio tiempo. los ejemplos más conocidos son los agujeros negros : si la masa se ??????comprime en una región suficientemente compacta del espacio (como se especifica en la conjetura aro , la escala de longitud de referencia es el radio de Schwarzschild), no hay luz desde el interior puede escapar al exterior. Dado que ningún objeto puede adelantar a un pulso de luz, toda la materia interior está encarcelado también. Passage desde el exterior a la interior es todavía posible, lo que demuestra que el límite, del agujero negro horizonte , no es una barrera física.

La ergosfera de unagujero negro en rotación, que desempeña un papel clave a la hora de extraer la energía de un agujero negro

Los primeros estudios de los agujeros negros se basó en soluciones explícitas de las ecuaciones de Einstein, en particular el esféricamente simétrica solución de Schwarzschild (utilizado para describir un agujero negro estático) y el axisimétrico solución de Kerr (utilizado para describir una rotación del agujero negro estacionaria, y la introducción de características interesantes, como la ergosfera). El uso de la geometría global, estudios posteriores han revelado propiedades más generales de los agujeros negros. A la larga, son más bien simples objetos caracterizados por once parámetros que especifican la energía , cantidad de movimiento , momento angular , ubicación en un momento determinado y la carga eléctrica . Esto se afirma por los teoremas de singularidad del agujero negro: "los agujeros negros no tienen pelo", es decir, no hay señas de identidad como los peinados de los seres humanos. Independientemente de la complejidad de un objeto gravitante colapsar para formar un agujero negro, el objeto de que los resultados (habiendo emiten ondas gravitatorias) es muy simple.

Aún más notable, hay un conjunto general de las leyes conocidas como la mecánica de los agujeros negros, que es análoga a la leyes de la termodin??mica. , por ejemplo, por la segunda ley de la mecánica de los agujeros negros, el área del horizonte de sucesos de un agujero negro en general nunca disminuirá con el tiempo , análoga a la entropía de un sistema termodinámico. Esto limita la energía que se puede extraer por medio clásicas de un agujero negro en rotación (por ejemplo, mediante el proceso de Penrose). Hay fuertes indicios de que las leyes de la mecánica de los agujeros negros son, de hecho, un subconjunto de las leyes de la termodinámica, y que el área del agujero negro es proporcional a su entropía. Esto conduce a una modificación de las leyes originales de la mecánica de agujeros negros: por ejemplo, como la segunda ley de la mecánica de los agujeros negros se convierte en parte de la segunda ley de la termodinámica, es posible que el área del agujero negro para disminuir-el tiempo que aseguran otros procesos que, en general, la entropía aumenta. Como termodinámico objetos con una temperatura que no sea cero, los agujeros negros deberían emitir radiación térmica. Cálculos semi-clásicas indican que de hecho lo hacen, con la gravedad de la superficie en el papel de la temperatura en la ley de Planck. Esta radiación se conoce como radiación de Hawking (cf. la sección de la teoría cuántica , a continuación).

Hay otros tipos de horizontes. En un universo en expansión, un observador puede encontrar que algunas regiones del pasado no pueden ser observados (" horizonte de partículas "), y en algunas regiones del futuro no pueden ser influenciados (horizonte de sucesos). Incluso en un espacio plano de Minkowski, cuando descrito por un observador acelerado ( espacio Rindler), habrá horizontes asociados con una radiación semi-clásica conocida como radiación Unruh.

Singularidades

Otra característica inquietante-generales-y bastante de la relatividad general es la aparición de los límites espacio-temporales conocidos como singularidades. Espacio-tiempo puede ser explorado por el seguimiento de tipo tiempo y lightlike geodésicas-todas las formas posibles que la luz y las partículas en caída libre pueden viajar. Pero algunas de las soluciones de las ecuaciones de Einstein tienen -regiones "bordes irregulares" conocidos como singularidades espacio-tiempo, donde los caminos de luz y partículas que caen vienen a un final abrupto, y la geometría se convierte en mal definidos. En los casos más interesantes, se trata de "singularidades de curvatura", donde las cantidades geométricas que caracterizan a la curvatura del espacio-tiempo, como el escalar de Ricci, adquieren valores infinitos. Ejemplos de espacio-tiempos Conocida con futuros singularidades-donde líneas de universo de fin son la solución de Schwarzschild, que describe una singularidad dentro de un agujero negro estático eterna, o la solución de Kerr con su singularidad en forma de anillo interior de un agujero negro en rotación eterna. La Friedmann-Lemaître soluciones-Walker -Robertson y otros espacio-tiempos que describen universos, tienen singularidades últimas líneas de universo en el que comienza, es decir, grandes explosión singularidades, y algunos tienen singularidades futuros ( Big Crunch) también.

. Teniendo en cuenta que estos ejemplos son todos altamente simétrica y por lo tanto simplifica-es tentador concluir que la aparición de singularidades es un artefacto de idealización Los famosos teoremas de singularidad, probaron utilizando los métodos de la geometría global, dicen lo contrario: singularidades son una característica genérica de generales relatividad, e inevitable una vez que el colapso de un objeto con propiedades de materia realistas ha procedido más allá de una cierta etapa y también en el comienzo de una amplia clase de expansión universos. Sin embargo, los teoremas dicen poco acerca de las propiedades de las singularidades, y gran parte de la investigación actual se dedica a la caracterización de la estructura genérica de estas entidades (por ejemplo, por la hipótesis de la llamada conjetura BKL). La hipótesis de la censura cósmica establece que todas las singularidades futuros realistas (no perfecta simetrías, la materia con propiedades realistas) se ocultan con seguridad lejos detrás de un horizonte, y por tanto invisible a todos los observadores distantes. Aunque todavía no existe una prueba formal, simulaciones numéricas ofrecen elementos de prueba de su validez.

Ecuaciones de evolución

Cada solución de la ecuación de Einstein abarca toda la historia de un universo que no es sólo una instantánea de cómo son las cosas, pero en su conjunto, posiblemente lleno de materia, espacio tiempo. él se describe el estado de la materia y la geometría en todas partes y en todo momento, en ese universo particular. Por esta razón, la teoría de Einstein parece ser diferente de la mayoría de otras teorías físicas, que especifican ecuaciones de evolución de los sistemas físicos: si el sistema está en un estado dado en algún momento dado, las leyes de la física permiten la extrapolación hacia el pasado o el futuro. Otras diferencias entre la gravedad de Einstein y otros campos son que el primero es libre interacción (es decir, no lineal, incluso en ausencia de otros campos), y que no tiene ninguna estructura el fondo fijo escenario mismo evoluciona como el drama cósmico es jugado.

Para entender las ecuaciones de Einstein como ecuaciones diferenciales parciales , es útil para formular de una manera que se describe la evolución del universo en el tiempo. Esto se hace en las llamadas formulaciones "3 + 1", donde el espacio-tiempo se divide en tres dimensiones espaciales y una dimensión temporal. El ejemplo más conocido es el formalismo ADM. Estas descomposiciones muestran que las ecuaciones de evolución espacio-tiempo de la relatividad general son bien educados: siempre soluciones existen, y se definen de forma única, se han especificado las condiciones iniciales una vez adecuados. Tales formulaciones de las ecuaciones de campo de Einstein son la base de la relatividad numérica.

Cantidades globales y cuasi-locales

La noción de ecuaciones de evolución está íntimamente vinculado con otro aspecto de la física relativista general. En la teoría de Einstein, que resulta ser imposible encontrar una definición general de una aparentemente simple propiedad, tales como el total de un sistema de masa (o energía ). La razón principal es que el campo como cualquier campo debe físico atribuirse una cierta energía, pero que se demuestra que es fundamentalmente imposible de localizar esa energía gravitacional.

Sin embargo, hay posibilidades para definir la masa total de un sistema, ya sea utilizando un hipotético "observador infinitamente distante" ( masa ADM) o simetrías adecuadas ( medios de Komar). Si uno excluye de la masa total del sistema de la energía que se llevaron hasta el infinito por las ondas gravitacionales, el resultado es la llamada masa Bondi en nulo el infinito. Al igual que en la física clásica, se puede demostrar que estas masas son positivos. Existen correspondientes definiciones globales para el impulso y momento angular . También ha habido un número de intentos de definir cuasi local de cantidades, tales como la masa de un sistema aislado formulado usando sólo cantidades definidas dentro de una región finita del espacio que contiene dicho sistema. La esperanza es obtener una cantidad útil para las declaraciones generales sobre los sistemas aislados, como una formulación más precisa de la conjetura aro.

Relación con la teoría cuántica

Si la relatividad general es considerado uno de los dos pilares de la física moderna, la teoría cuántica , la base de nuestra comprensión de la materia de partículas elementales a la física del estado sólido, es el otro. Sin embargo, sigue siendo una pregunta abierta de cómo los conceptos de la teoría cuántica pueden conciliarse con las de la relatividad general.

Teoría cuántica de campos en el espacio-tiempo curvo

Ordinaria teorías cuánticas de campos , que forman la base de la moderna física de partículas elementales , se definen en plana espacio de Minkowski, que es una excelente aproximación a la hora de describir el comportamiento de las partículas microscópicas en campos gravitatorios débiles como las que se encuentran en la Tierra. Para describir situaciones en las que la gravedad es lo suficientemente fuerte como para influir (quantum) importa, pero no lo suficientemente fuertes como para requerir de cuantificación en sí, los físicos han formulado teorías cuánticas de campos en el espacio-tiempo curvo. Estas teorías se basan en la relatividad general clásica para describir un fondo curva el espacio-tiempo, y definir una teoría cuántica de campos generalizada para describir el comportamiento de la materia cuántica dentro de ese espacio-tiempo. El uso de este formalismo, se puede demostrar que los agujeros negros emiten un espectro de cuerpo negro de partículas conocidas como radiación de Hawking , dando lugar a la posibilidad de que se evaporan con el tiempo. Como se ha mencionado brevemente más arriba , esta radiación juega un papel importante para la termodinámica de los agujeros negros.

La gravedad cuántica

La demanda de coherencia entre una descripción cuántica de la materia y una descripción geométrica del espacio-tiempo, así como la aparición de singularidades (en escalas de longitud curvatura convierten microscópica), indica la necesidad de una teoría completa de la gravedad cuántica: para una descripción adecuada de la interior de los agujeros negros, y del universo muy temprano, se requiere una teoría en la que la gravedad y la geometría del espacio-tiempo asociado se describen en el lenguaje de la física cuántica. A pesar de grandes esfuerzos, ninguna teoría completa y consistente de la gravedad cuántica se conoce actualmente, a pesar de que existe un número de candidatos prometedores.

Proyección de uncolector de Calabi-Yau, una de las formas decompactifying las dimensiones extra postuladas por la teoría de cuerdas

Los intentos de generalizar teorías cuánticas de campos comunes, utilizados en física de partículas elementales para describir las interacciones fundamentales, a fin de incluir la gravedad han dado lugar a graves problemas. A bajas energías, este enfoque tiene éxito, en que resulta en un aceptable eficaz (quantum) la teoría de campo de la gravedad. A muy altas energías, sin embargo, el resultado son modelos desprovistos de todo poder predictivo (" no-renormalizabilidad ").

Simple red de giro del tipo utilizado en la gravedad cuántica de bucles

Un intento de superar estas limitaciones es la teoría de cuerdas , una teoría cuántica no de partículas puntuales, pero de minutos objetos extendidos unidimensionales. La teoría promete ser una descripción unificada de todas las partículas e interacciones, incluyendo la gravedad; el precio a pagar son características inusuales, tales como seis dimensiones extra del espacio, además de los tres habituales. En lo que se llama la segunda revolución de las supercuerdas, se conjetura que tanto la teoría de cuerdas y una unificación de la relatividad general y la supersimetría conocido como formulario de supergravedad parte de un modelo de once dimensiones hipótesis conocida como teoría-M , lo que constituiría una definida forma única y coherente teoría de la gravedad cuántica.

Otro enfoque comienza con los procedimientos de cuantificación canónicos de la teoría cuántica. Utilizando el valor-formulación inicial de la relatividad general (cf. el apartado de ecuaciones de evolución, por encima ), el resultado es la ecuación de Wheeler-DeWitt (un análogo de la ecuación de Schrödinger) que, lamentablemente, resulta ser mal definida. Sin embargo, con la introducción de lo que ahora se conoce como variables de Ashtekar, esto conduce a un modelo prometedor conocido como la gravedad cuántica de bucles. El espacio es representado por una estructura similar a una red llamada red de centrifugado, evolucionando con el tiempo en pasos discretos.

Dependiendo de qué características de la relatividad general y la teoría cuántica son aceptadas sin cambios, y de qué nivel se introducen cambios, hay muchos otros intentos de llegar a una teoría viable de la gravedad cuántica, algunos ejemplos siendo triangulaciones dinámicas, juegos causales,modelos twistores o losmodelos basados ??????en rutas de acceso integral dela cosmología cuántica.

Todas las teorías candidatos todavía tienen importantes problemas formales y conceptuales que superar. También se enfrentan al problema común de que, hasta ahora, no hay manera de poner las predicciones de gravedad cuántica a pruebas experimentales (y por tanto de decidir entre los candidatos en sus predicciones varían), aunque hay esperanza de que esto cambie de datos como los futuros de cosmológico observaciones y experimentos de física de partículas que se disponga.

Estado actual

La relatividad general se ha convertido en un modelo de gran éxito de la gravitación y la cosmología, que ha pasado hasta ahora cada prueba observacional y experimental inequívoca. Aun así, hay fuertes indicios de la teoría está incompleta. El problema de la gravedad cuántica y la cuestión de la realidad de las singularidades del espacio-tiempo permanecen abiertas. Datos de observación que se toma como evidencia de la energía oscura y la materia oscura podría indicar la necesidad de una nueva física, y si bien el llamado Pioneer anomalía todavía podría admitir una explicación convencional, también podría ser un presagio de una nueva física. Incluso tomada tal cual, la relatividad general es rico en posibilidades para una mayor exploración. Relativistas matemáticos tratan de comprender la naturaleza de las singularidades y las propiedades fundamentales de las ecuaciones de Einstein, y simulaciones por ordenador cada vez más potentes (como los que describe la fusión de agujeros negros) se ejecute. La carrera por la primera detección directa de ondas gravitacionales continúa a buen ritmo, con la esperanza de crear oportunidades para poner a prueba la validez de la teoría de campos gravitatorios mucho más fuertes de lo que ha sido posible hasta la fecha. Más de noventa años después de su publicación, la relatividad general sigue siendo un área muy activa de investigación.