Introducci??n a la relatividad general
Antecedentes
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organiz?? esta selecci??n. Antes de decidir sobre el patrocinio de un ni??o, ??por qu?? no aprender sobre diferentes obras de caridad de patrocinio primero ?
| La relatividad general |
|---|
 |
| Introducci??n Formulaci??n matem??tica Recursos |
Conceptos fundamentales |
Fen??menos Problema de Kepler ?? Lentes ?? Ondas Torsi??n por arrastre ?? Efecto geod??sico Horizonte de eventos ?? Singularidad Agujero negro |
Ecuaciones Gravedad linealizada Formalismo post-newtoniana Ecuaciones de campo de Einstein Ecuaci??n geod??sica Ecuaciones de Friedmann ADM formalismo BSSN formalismo Ecuaci??n de Hamilton-Jacobi-Einstein |
Teor??as avanzadas Kaluza-Klein La gravedad cu??ntica |
Soluciones Schwarzschild Reissner-Nordstr??m ?? G??del Kerr ?? Kerr-Newman Kasner ?? Taub-NUT ?? Milne ?? Robertson-Walker de onda pp ?? polvo van Stockum |
Los cient??ficos Einstein ?? Lorentz ?? Hilbert ?? Poincar?? ?? Schwarzschild ?? Sitter ?? Reissner ?? Nordstr??m ?? Weyl ?? Eddington ?? Friedman ?? Milne ?? Zwicky ?? Lema??tre ?? G??del ?? Wheeler ?? Robertson ?? Bardeen ?? Walker ?? Kerr ?? Chandrasekhar ?? Ehlers ?? Penrose ?? Hawking ?? Taylor ?? Hulse ?? Stockum ?? Taub ?? Hombre Nuevo Yau ?? Thorne otros |
Espacio Tiempo Espacio Tiempo Espaciotiempo de Minkowski Diagramas espacio-tiempo Espacio-tiempo en la relatividad general |
La relatividad general es una la teor??a de la gravitaci??n que fue desarrollada por Albert Einstein entre 1907 y 1915. De acuerdo con la relatividad general, la atracci??n gravitacional observada entre masas resultados de su deformaci??n de espacio y tiempo.
A principios del siglo 20, La ley de la gravitaci??n universal de Newton hab??a sido aceptada por m??s de 200 a??os como una descripci??n v??lida de la fuerza gravitacional entre masas. En el modelo de Newton, la gravedad es el resultado de una fuerza de atracci??n entre los objetos masivos. Aunque incluso Newton estaba preocupado por la naturaleza desconocida de esa fuerza, el marco b??sico tuvo un gran ??xito en describir el movimiento.
Experimentos y observaciones muestran que la descripci??n de la gravitaci??n de Einstein explica varios efectos que son inexplicables por la ley de Newton, como anomal??as en el minuto ??rbitas de Mercurio y otros planetas . La relatividad general predice tambi??n novedosos efectos de la gravedad, como ondas gravitacionales, lente gravitatoria y un efecto de la gravedad sobre el tiempo conocido como la dilataci??n del tiempo gravitacional. Muchas de estas predicciones se han confirmado por el experimento, mientras que otros son objeto de la investigaci??n en curso. Por ejemplo, aunque hay evidencia indirecta de ondas gravitacionales, la evidencia directa de su existencia sigue siendo buscado por varios equipos de cient??ficos en experimentos como el LIGO y GEO 600 proyectos.
La relatividad general se ha convertido en una herramienta esencial en la moderna astrof??sica . Proporciona la base para la comprensi??n actual de los agujeros negros , regiones del espacio donde la atracci??n gravitacional es tan fuerte que ni siquiera la luz puede escapar. Su fuerte gravedad se cree que es responsable de la intensa radiaci??n emitida por ciertos tipos de objetos astron??micos (como n??cleos gal??cticos activos o microcu??sares). La relatividad general tambi??n es parte del marco de la norma Big Bang modelo de la cosmolog??a .
Aunque la relatividad general no es la ??nica teor??a relativista de la gravedad, es el m??s simple tal teor??a de que es consistente con los datos experimentales. Sin embargo, una serie de preguntas abiertas siguen siendo, el m??s fundamental de que es la forma general de la relatividad se puede reconciliar con las leyes de la f??sica cu??ntica para producir una teor??a completa y auto-consistente de la gravedad cu??ntica.
De especial a la relatividad general
En septiembre de 1905, Albert Einstein public?? su teor??a de la relatividad especial , que reconcilia las leyes del movimiento de Newton con electrodin??mica (la interacci??n entre los objetos con carga el??ctrica ). La relatividad especial introdujo un nuevo marco para toda la f??sica proponiendo nuevos conceptos de espacio y tiempo. Algunas teor??as f??sicas luego aceptados eran incompatibles con ese marco; un ejemplo clave era la teor??a de Newton de la gravedad , que describe la atracci??n mutua que experimentan los cuerpos debido a su masa.
Varios f??sicos, incluido Einstein, buscaron una teor??a que concilie ley de la gravedad y de la relatividad especial de Newton. S??lo la teor??a de Einstein demostr?? ser consistente con los experimentos y observaciones. Para entender las ideas b??sicas de la teor??a, es instructivo a seguir el pensamiento de Einstein entre 1907 y 1915, de su sencillo pensado experimento con un observador en ca??da libre a su teor??a totalmente geom??trica de la gravedad.
Principio de equivalencia
Una persona en una ca??da libre ascensor experimenta ingravidez, y objetos ya sea flotar inm??vil o la deriva a una velocidad constante. Como todo en el ascensor est?? cayendo juntos, ning??n efecto gravitacional se puede observar. De esta manera, las experiencias de un observador en ca??da libre son indistinguibles de los de un observador en el espacio profundo, lejos de cualquier fuente significativa de la gravedad. Dichos observadores son los ("inercia") observadores privilegiados Einstein describi?? en su teor??a de la relatividad especial : los observadores para quienes la luz viaja a lo largo de l??neas rectas a velocidad constante.
Einstein plante?? la hip??tesis de que las experiencias similares de observadores de ingravidez y observadores inerciales en la relatividad especial representaban una propiedad fundamental de la gravedad, y ??l hizo esta la piedra angular de su teor??a de la relatividad general, formalizado en su principio de equivalencia. En t??rminos generales, los principio establece que una persona en un ascensor en ca??da libre no puede decir que est?? en ca??da libre. Cada experimento en un entorno de este tipo ca??da libre tiene los mismos resultados que lo har??a para un observador en reposo o en movimiento uniforme en el espacio profundo, lejos de todas las fuentes de la gravedad.
La gravedad y la aceleraci??n

La mayor??a de los efectos de la gravedad se desvanecen en ca??da libre, pero los efectos que parecen las mismas que las de la gravedad pueden ser producidos por un acelerado marco de referencia. Un observador en una habitaci??n cerrada no puede decir cu??l de las siguientes es verdadera:
- Los objetos se caen al suelo porque la habitaci??n est?? descansando en la superficie de la Tierra y los objetos est??n siendo derribadas por la gravedad.
- Los objetos se caen al suelo porque la habitaci??n es a bordo de un cohete en el espacio, que se acelera a 9,81 m / s 2 y est?? lejos de cualquier fuente de gravedad. Los objetos est??n siendo arrastradas hacia el suelo por la misma "fuerza inercial" que presiona el conductor de un coche acelerando en el respaldo de su asiento.
A la inversa, cualquier efecto observado en un marco de referencia acelerado tambi??n se debe observar en un campo gravitacional de la resistencia correspondiente. Este principio permite Einstein para predecir varios efectos novedosos de gravedad en 1907, como se explica en la siguiente secci??n .
Un observador en un sistema de referencia acelerado debe introducir lo que los f??sicos llaman fuerzas ficticias para dar cuenta de la aceleraci??n experimentada por ??l mismo y los objetos que le rodean. Un ejemplo, la fuerza de presi??n que el conductor de un coche acelerando en su asiento, ya se ha mencionado; otra es la fuerza puede sentirse tirando los brazos hacia arriba y hacia fuera si se intenta dar vueltas como un trompo. Visi??n maestro de Einstein fue que el constante tir??n, familiar del campo gravitatorio de la Tierra es fundamentalmente el mismo que estas fuerzas ficticias. La magnitud aparente de las fuerzas ficticias siempre parece ser proporcional a la masa de cualquier objeto sobre el que act??an - por ejemplo, el asiento del conductor ejerce suficiente fuerza para acelerar el conductor en el mismo ritmo que el coche. Por analog??a, Einstein propuso que un objeto en un campo gravitatorio debe sentir una fuerza gravitatoria proporcional a su masa, que se concreta en La ley de Newton de la gravitaci??n.
Consecuencias f??sicas
En 1907, Einstein a??n tardaron ocho a??os lejos de completar la teor??a general de la relatividad. No obstante, ??l fue capaz de hacer una serie de nuevas predicciones comprobables, que se basaban en su punto de partida para el desarrollo de su nueva teor??a: el principio de equivalencia.

El primer efecto es la nueva cambio de frecuencia gravitacional de la luz. Considere dos observadores a bordo de un cohete de la nave acelerando. A bordo de un buque de este tipo no es un concepto natural de "arriba" y "abajo": la direcci??n en la que la nave acelera es "arriba", y los objetos no unidos a acelerar en la direcci??n contraria, cayendo "hacia abajo". Supongamos que uno de los observadores es "m??s alto" que el otro. Cuando el observador inferior env??a una se??al de luz para el observador m??s alto, la aceleraci??n hace que la luz sea desplazada al rojo , como puede ser calculada a partir de la relatividad especial ; el segundo observador medir?? un menor frecuencia de la luz que el primero. Por el contrario, la luz enviada desde el observador m??s alta a la m??s baja es desplazada al azul, es decir, desplazado hacia frecuencias m??s altas. Einstein argument?? que tales cambios de frecuencia tambi??n deben tener en cuenta en un campo gravitatorio. Esto se ilustra en la figura de la izquierda, que muestra una onda de luz que es gradualmente de color rojo-desplazado como funciona su camino hacia arriba contra la aceleraci??n de la gravedad. Este efecto ha sido confirmado experimentalmente, como se describe a continuaci??n .
Este desplazamiento de frecuencia gravitacional corresponde a una dilataci??n gravitacional del tiempo: Desde el observador "superior" mide la misma onda de luz a una frecuencia m??s baja que el observador "inferior", el tiempo debe ser pasar m??s r??pido para el observador m??s alto. Por lo tanto, el tiempo corre m??s despacio para observadores que son m??s bajos en un campo gravitatorio.
Es importante destacar que, para cada observador, no hay cambios observables del flujo del tiempo para los eventos o procesos que est??n en reposo en su marco de referencia. Cinco minutos-huevos como timed por el reloj de cada observador tienen la misma consistencia; s??lo un a??o pasa en cada reloj, cada observador edades por esa cantidad; cada reloj, en definitiva, est?? en perfecto acuerdo con todos los procesos sucediendo en sus inmediaciones. Es s??lo cuando los relojes se comparan entre observadores independientes que uno puede notar que el tiempo corre m??s despacio para el observador m??s bajo que para el superior. Este efecto es minutos, pero tambi??n se ha confirmado experimentalmente en m??ltiples experimentos, como se describe a continuaci??n .
De manera similar, Einstein predijo la desviaci??n gravitacional de la luz: en un campo gravitacional, la luz es desviada hacia abajo. Cuantitativamente, sus resultados fueron por un factor de dos; la derivaci??n correcta requiere una formulaci??n m??s completa de la teor??a de la relatividad general, no s??lo el principio de equivalencia.
Efectos de la marea

La equivalencia entre los efectos gravitacionales e inerciales no constituye una teor??a completa de la gravedad. Cuando se trata de explicar la gravedad cerca de nuestra propia ubicaci??n en la superficie de la Tierra, haciendo notar que nuestro marco de referencia no est?? en ca??da libre, por lo que fuerzas ficticias son de esperar, proporciona una explicaci??n adecuada. Pero un sistema de referencia en ca??da libre en un lado de la Tierra no puede explicar por qu?? las personas en el lado opuesto de la Tierra experimentan una fuerza gravitatoria en la direcci??n opuesta.
Una manifestaci??n m??s b??sica del mismo efecto implica dos cuerpos que caen al lado del otro hacia la Tierra. En un marco de referencia que se encuentra en ca??da libre al lado de estos ??rganos, que parecen flotar en la ingravidez - pero no es exactamente as??. Estos cuerpos no est??n cayendo precisamente en la misma direcci??n, pero hacia un ??nico punto en el espacio: es decir, de la Tierra el centro de gravedad . En consecuencia, existe una componente de movimiento de cada cuerpo hacia la otra (ver la figura). En un entorno peque??o, como un ascensor en ca??da libre, esta aceleraci??n relativa es min??scula, mientras que para paracaidistas en lados opuestos de la Tierra, el efecto es grande. Estas diferencias en la fuerza tambi??n son responsables de las mareas en los oc??anos de la Tierra, por lo que el t??rmino " efecto de marea "se utiliza para este fen??meno.
La equivalencia entre la inercia y la gravedad no puede explicar los efectos de marea - no puede explicar las variaciones en el campo gravitatorio. Para ello, se necesita una teor??a que describe la forma en que la materia (tales como la gran masa de la Tierra) afecta al medio ambiente de inercia alrededor de ella.
De la aceleraci??n a la geometr??a
Al explorar la equivalencia de la gravedad y la aceleraci??n, as?? como el papel de las fuerzas de marea, Einstein descubri?? varias analog??as con la geometr??a de superficies. Un ejemplo es la transici??n de un sistema de referencia inercial (en el que las part??culas libres costa a lo largo de trayectorias rectas a velocidades constantes) a un marco de referencia de rotaci??n (en el que los t??rminos adicionales correspondientes a fuerzas ficticias que se han introducido con el fin de explicar el movimiento de part??culas): esto es an??logo a la transici??n de un cartesiano sistema (en el que las l??neas de coordenadas son las l??neas rectas) coordinar a un curvada sistema (donde coordinar l??neas no tienen por qu?? ser recto) de coordenadas.
Una analog??a m??s profundo relaciona las fuerzas de marea con una propiedad de las superficies llamada curvatura. Para los campos gravitacionales, la ausencia o presencia de las fuerzas de marea determina si o no la influencia de la gravedad puede ser eliminado por la elecci??n de un marco de referencia que cae libremente. Del mismo modo, la ausencia o presencia de curvatura determina si o no una superficie es equivalente a un avi??n . En el verano de 1912, inspirado por estas analog??as, Einstein busc?? una formulaci??n geom??trica de la gravedad.
Los objetos elementales de geometr??a - puntos, l??neas , tri??ngulos - tradicionalmente se definen en tres dimensiones el espacio o en dos dimensiones superficies. En 1907, el matem??tico Hermann Minkowski (que fue el ex profesor de matem??ticas de Einstein en Swiss Federal Polit??cnica) introdujo una formulaci??n geom??trica de Einstein teor??a especial de la relatividad en el que la geometr??a no s??lo inclu??a espacio, sino tambi??n el tiempo. La entidad b??sica de esta nueva geometr??a es de cuatro dimensional espacio tiempo. Las ??rbitas de los cuerpos en movimiento son curvas en el espacio-tiempo; las ??rbitas de los cuerpos que se mueven a velocidad constante sin cambiar de direcci??n corresponden a las l??neas rectas.
Para superficies, la generalizaci??n de la geometr??a de un plano - una superficie plana - a la de una superficie curva general hab??a sido descrita en el siglo 19 por Carl Friedrich Gauss . Esta descripci??n ha su vez ha generalizado a espacios de dimensiones superiores en un formalismo matem??tico introducido por Bernhard Riemann en la d??cada de 1850. Con la ayuda de La geometr??a de Riemann, Einstein formul?? una descripci??n geom??trica de la gravedad en la que el espacio-tiempo de Minkowski se sustituye por distorsionada, espacio-tiempo curvado, al igual que las superficies curvas son una generalizaci??n de superficies planas ordinarias.
Despu??s de que ??l se hab??a dado cuenta de la validez de esta analog??a geom??trica, tom?? Einstein otros tres a??os para encontrar la piedra angular que faltaba de su teor??a: las ecuaciones que describen c??mo importa curvatura influencias del espacio-tiempo. Habiendo formulado lo que ahora se conoce como Las ecuaciones de Einstein (o, m??s precisamente, sus ecuaciones de campo de la gravedad), present?? su nueva teor??a de la gravedad en varias sesiones del Academia Prusiana de las Ciencias a finales de 1915.
Geometr??a y la gravitaci??n
Parafraseando John Wheeler, teor??a geom??trica de Einstein de la gravedad se puede resumir as??: el espacio-tiempo le dice a la materia c??mo moverse; la materia le dice el espacio-tiempo c??mo curvarse. Lo que esto significa es abordado en las tres secciones siguientes, que exploran el movimiento de las llamadas part??culas de prueba, estudiar?? las propiedades de la materia sirven como fuente de gravedad, y, por ??ltimo, introducir las ecuaciones de Einstein, que se refieren estas propiedades de la materia a la curvatura del espacio-tiempo.
Sondeo del campo gravitatorio

Con el fin de trazar la influencia gravitatoria de un cuerpo, es ??til pensar en lo que los f??sicos llaman sonda o part??culas de prueba: las part??culas que se ven influidas por la gravedad, pero que son tan peque??o y ligero que podemos descuidar su propio efecto gravitacional. En ausencia de la gravedad y otras fuerzas externas, una part??cula de prueba se desplaza a lo largo de una l??nea recta a una velocidad constante. En el lenguaje de el espacio-tiempo, esto es equivalente a decir que tales part??culas de prueba se mueven a lo largo de recta l??neas de mundo en el espacio-tiempo. En presencia de la gravedad, el espacio-tiempo es no euclidiana, o puede que no existan l??neas curvas mundo, y en el espacio-tiempo curvo rectas. En lugar de ello, las part??culas de prueba se mueven a lo largo de l??neas llamadas geod??sicas, que son "lo m??s recto posible".
Una simple analog??a es la siguiente: En geodesia, la ciencia de medir el tama??o y la forma de la Tierra, una geod??sica (de "geo" griega, la Tierra, y "daiein", para dividir) es la ruta m??s corta entre dos puntos de la superficie de la Tierra. Aproximadamente, tal ruta es una segmento de una gran c??rculo, tal como una l??nea de longitud o el ecuador . Estos caminos no son ciertamente recta, simplemente porque tienen que seguir la curvatura de la superficie de la Tierra. Pero son tan recta como sea posible sujetas a esta restricci??n.
Las propiedades de geod??sicas difieren de las de l??neas rectas. Por ejemplo, en un avi??n, l??neas paralelas nunca se encuentran, pero esto no es as?? para las geod??sicas en la superficie de la Tierra: por ejemplo, las l??neas de longitud son paralelas al ecuador, pero se cruzan en los polos. An??logamente, las l??neas mundiales de part??culas de prueba en ca??da libre son geod??sicas del espacio-tiempo, las l??neas m??s rectas posibles en el espacio-tiempo. Pero todav??a hay diferencias cruciales entre ellos y las l??neas rectas realmente que pueden ser rastreados en el espacio-tiempo libre de gravedad de la relatividad especial. En la relatividad especial, geod??sicas paralelas permanecen paralelas. En un campo gravitacional con efectos de marea, esto no es as??, en general, ser el caso. Si, por ejemplo, dos cuerpos est??n inicialmente en reposo respecto a la otra, pero luego se dejan caer en el campo gravitatorio de la Tierra, se mueven una hacia la otra a medida que caen hacia el centro de la Tierra.
En comparaci??n con los planetas y otros cuerpos astron??micos, los objetos de la vida cotidiana (personas, coches, casas, incluso monta??as) tienen poca masa. Cuando se trata de este tipo de objetos, las leyes que rigen el comportamiento de las part??culas de prueba son suficientes para describir lo que sucede. En particular, con el fin de desviar una part??cula de prueba de su trayectoria geod??sica, una fuerza externa se debe aplicar. Una persona sentada en una silla est?? tratando de seguir una geod??sica, es decir, a caer libremente hacia el centro de la Tierra. Pero la silla se aplica una fuerza hacia arriba externa prevenir la persona se caiga. De esta manera, la relatividad general explica la experiencia diaria de la gravedad en la superficie de la Tierra no como el tir??n hacia abajo de una fuerza gravitacional, sino como el empuje hacia arriba de fuerzas externas. Estas fuerzas desv??an todos los cuerpos que descansan sobre la superficie de la Tierra desde las geod??sicas que de otro modo seguir. Para los objetos de materia cuya propia influencia gravitatoria no puede ser descuidado, las leyes del movimiento son un poco m??s complicado que para part??culas de prueba, si bien es cierto que el espacio-tiempo le dice a la materia c??mo moverse.
Las ecuaciones de Einstein
Las ecuaciones de Einstein son la pieza central de la relatividad general. Proporcionan una formulaci??n precisa de la relaci??n entre la geometr??a del espacio-tiempo y las propiedades de la materia, utilizando el lenguaje de las matem??ticas. M??s concretamente, se formulan utilizando los conceptos de La geometr??a de Riemann, en la que las propiedades geom??tricas de un espacio (o un espacio-tiempo) son descritos por una cantidad llamada una m??trica. La m??trica codifica la informaci??n necesaria para calcular las nociones geom??tricas fundamentales de la distancia y el ??ngulo en un espacio curvo (o espacio-tiempo).

Una superficie esf??rica como la de la Tierra ofrece un ejemplo sencillo. La ubicaci??n de cualquier punto de la superficie puede ser descrita por dos coordenadas: la geogr??fica latitud y de longitud. A diferencia de las coordenadas cartesianas del avi??n, coordinan las diferencias no son las mismas que las distancias en la superficie, como se muestra en el diagrama de la derecha: para alguien en el ecuador, se mueve 30 grados de longitud oeste (l??nea magenta) corresponde a una distancia de aproximadamente 3.300 kilometros (2.100 millas). Por otro lado, alguien a una latitud de 55 grados, movimiento 30 grados de longitud oeste (l??nea azul) cubre una distancia de apenas 1.900 kilometros (1.200 millas). Coordenadas, por tanto, no proporcionan suficiente informaci??n para describir la geometr??a de una superficie esf??rica, o incluso la geometr??a de cualquier espacio m??s complicado o espacio-tiempo. Esa informaci??n es precisamente lo que est?? codificado en la m??trica, que es una funci??n definida en cada punto de la superficie (o espacio, o espacio-tiempo) y se relaciona la diferencia de coordenadas a diferencias en la distancia. Todas las dem??s cantidades que son de inter??s en la geometr??a, tales como la longitud de cualquier curva dada, o el ??ngulo en el que dos curvas se encuentran, se pueden calcular a partir de esta funci??n m??trica.
La funci??n de m??trica y su tasa de cambio de punto a punto pueden ser utilizados para definir una cantidad geom??trica llamada Tensor de curvatura de Riemann, que describe exactamente c??mo se curva en cada punto del espacio (o espacio-tiempo). En la relatividad general, la m??trica y el tensor de curvatura de Riemann son cantidades definidas en cada punto del espacio-tiempo. Como ya se ha mencionado, el contenido de materia del espacio-tiempo define otra cantidad, la Energ??a-momento tensor T, y el principio de que "el espacio-tiempo le dice a la materia c??mo moverse, y la materia dice el espacio-tiempo c??mo curvarse" significa que estas cantidades deben estar relacionados entre s??. Einstein formul?? esta relaci??n mediante el tensor de curvatura de Riemann y la m??trica para definir otra cantidad geom??trica G, que ahora se llama la Tensor de Einstein, que describe algunos aspectos de la forma en el espacio-tiempo es curvo. Ecuaci??n de Einstein a continuaci??n que
es decir, hasta un m??ltiplo constante, la cantidad G (que mide la curvatura) se equipara con la cantidad T (que mide el contenido de materia). Las constantes que intervienen en esta ecuaci??n reflejan las diferentes teor??as que en su construcci??n: π es una de las constantes b??sicos de la geometr??a, G es la constante gravitacional que ya est?? presente en la gravedad newtoniana, y c es la velocidad de la luz , la constante fundamental en la relatividad especial.
Esta ecuaci??n se refiere a menudo en plural como las ecuaciones de Einstein, ya que las cantidades G y T son cada determinados por varias funciones de las coordenadas de espacio-tiempo, y las ecuaciones equivale cada una de estas funciones de los componentes. Una soluci??n de estas ecuaciones describe una geometr??a particular de espacio y tiempo; Por ejemplo, el Soluci??n de Schwarzschild describe la geometr??a alrededor de una masa no giratoria esf??rica tal como una estrella o un agujero negro , mientras que la Soluci??n Kerr describe un agujero negro en rotaci??n. Todav??a otras soluciones pueden describir un onda gravitatoria o, en el caso de la Soluci??n Friedmann-Lema??tre-Robertson-Walker, un universo en expansi??n. La soluci??n m??s sencilla es la uncurved Espaciotiempo de Minkowski, el espacio-tiempo descrito por la relatividad especial.
Las pruebas experimentales
Ninguna teor??a cient??fica es apod??cticamente cierto; cada uno es un modelo que debe ser comprobado por la experiencia. Ley de gravedad de Newton fue aceptada ya que represent?? el movimiento de los planetas y las lunas en el sistema solar con una precisi??n considerable. A medida que la precisi??n de las mediciones experimentales mejoraron gradualmente, se observaron algunas discrepancias con las predicciones de Newton, y estos se contabilizan en la teor??a general de la relatividad. Del mismo modo, las predicciones de la relatividad general tambi??n deben ser revisados con el experimento, y el propio Einstein ide?? tres pruebas ahora conocidas como las pruebas cl??sicas de la teor??a:

- La gravedad newtoniana predice que la orbitar la cual un solo planeta alrededor de una traza perfectamente esf??rica estrella debe ser una elipse . La teor??a de Einstein predice una curva m??s complicada: el planeta se comporta como si estuviera viajando por una elipse, pero al mismo tiempo, la elipse como un todo est?? girando lentamente alrededor de la estrella. En el diagrama de la derecha, la elipse predicho por la gravedad newtoniana se muestra en rojo, y parte de la ??rbita predicha por Einstein en azul. Para que un planeta en ??rbita alrededor del Sol, esta desviaci??n de las ??rbitas de Newton es conocido como el desplazamiento del perihelio an??malo. La primera medida de este efecto, para el planeta Mercurio , se remonta a 1859. Los resultados m??s precisos para Mercurio y de otros planetas hasta la fecha se basan en mediciones que se llevaron a cabo entre 1966 y 1990, utilizando radiotelescopios . La relatividad general predice que el cambio perihelio an??malo correcto para todos los planetas donde esta se puede medir con precisi??n ( Mercurio , Venus y la Tierra ).
- De acuerdo con la relatividad general, la luz no viaja a lo largo de l??neas rectas cuando se propaga en un campo gravitatorio. En cambio, es desviado en la presencia de cuerpos masivos. En particular, la luz estelar se desv??a cuando pasa cerca del Sol, dando lugar a cambios aparentes de hasta 1,75 segundos de arco en posiciones de las estrellas en el cielo nocturno (un segundo de arco es igual a 1/3600 de un grado ). En el marco de la gravedad newtoniana, un argumento heur??stica puede ser hecho que conduce a la desviaci??n de la luz por medio de esa cantidad. Los diferentes predicciones pueden ser probados mediante la observaci??n de las estrellas que est??n cerca del Sol durante un eclipse solar . De esta manera, una expedici??n brit??nica a ??frica Occidental en 1919, dirigida por Arthur Eddington, confirm?? que la predicci??n de Einstein era correcta, y las predicciones newtonianas mal, a trav??s de la observaci??n de la 05 1919 eclipse. Resultados de Eddington no eran muy precisos; observaciones subsiguientes de la desviaci??n de la luz de distante qu??sares por el Sol, que utilizan t??cnicas muy precisas de radioastronom??a, han confirmado los resultados de Eddington con significativamente mejor precisi??n (la primera de esas mediciones se remontan a 1967, el an??lisis global m??s reciente de 2004).
- Corrimiento al rojo gravitacional se midi?? por primera vez en un entorno de laboratorio en 1959 por Pound y Rebka. Tambi??n se ve en las mediciones astrof??sicas, en particular para la luz de escapar de la White Dwarf Sirius B . El relacionada efecto de la dilataci??n del tiempo gravitacional se ha medido mediante el transporte de los relojes at??micos a altitudes de entre decenas y decenas de miles de kil??metros (primero por Hafele y Keating en 1971; m??s precisa hasta la fecha por Gravity Probe A puso en marcha en 1976).
De estas pruebas, s??lo el avance del perihelio de Mercurio era conocido antes de la publicaci??n final de Einstein de la relatividad general en 1916. La confirmaci??n experimental posterior de sus otras predicciones, especialmente las primeras mediciones de la desviaci??n de la luz por el sol en 1919, catapult?? a Einstein estrellato internacional. Estas tres pruebas experimentales justificaron la adopci??n de la relatividad general sobre la teor??a de Newton y, de paso, a trav??s de una serie de alternativas a la relatividad general que se hab??an propuesto.

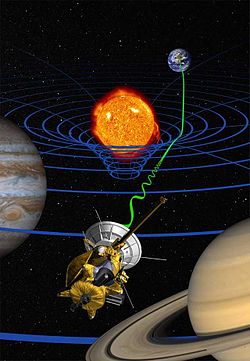
Otras pruebas de la relatividad general incluyen medidas de precisi??n de la Efecto Shapiro o retardo de tiempo gravitacional de la luz, la m??s reciente en 2002 por la Cassini sonda espacial. Una serie de pruebas se centra en los efectos predichos por la relatividad general para el comportamiento de giroscopios que viajan a trav??s del espacio. Uno de estos efectos, precesi??n geod??sica, ha sido probado con el Experimento Ranging Lunar Laser (mediciones de alta precisi??n de la ??rbita de la Luna ). Otra, que est?? relacionada con masas giratorias, se llama torsi??n por arrastre. Los efectos geod??sicos y torsi??n por arrastre fueron probados tanto por el Experimento sat??lite Gravity Probe B puso en marcha en 2004, con resultados que confirman la relatividad de entre 0,5% y 15%, respectivamente, a partir de diciembre de 2008.
Seg??n los est??ndares c??smicos, la gravedad en todo el sistema solar es d??bil. Dado que las diferencias entre las predicciones de Einstein y las teor??as de Newton son m??s pronunciados cuando la gravedad es fuerte, los f??sicos han sido durante mucho tiempo interesados en probar diferentes efectos relativistas en un entorno con comparativamente fuertes campos gravitatorios. Esto ha sido posible gracias a las observaciones de precisi??n de p??lsares binarios. En un sistema de este tipo estrella, dos altamente compacto estrellas de neutrones orbitan entre s??. Al menos uno de ellos es una p??lsar - un objeto astron??mico que emite un haz estrecho de ondas de radio. Estos rayos golpean la Tierra a intervalos muy regulares, de manera similar a la forma en que el rayo giratorio de un faro significa que un observador ve un abrir y cerrar faro, y se puede observar como una serie muy regular de pulsos. La relatividad general predice desviaciones espec??ficas de la regularidad de estos pulsos de radio. Por ejemplo, en momentos en que las ondas de radio pasan cerca de la otra estrella de neutrones, deben ser desviadas por el campo gravitatorio de la estrella. Los patrones de impulsos observados son impresionantemente cerca de los predichos por la relatividad general.
Un conjunto particular de observaciones se relaciona con aplicaciones pr??cticas eminentemente ??tiles, a saber, sistemas de navegaci??n por sat??lite, tales como la Sistema de posicionamiento global que se utiliza tanto para precisa posicionamiento y cronometraje. Tales sistemas se basan en dos conjuntos de relojes at??micos: los relojes a bordo de los sat??lites que orbitan la Tierra, y los relojes de referencia estacionados en la superficie de la Tierra. La relatividad general predice que estos dos conjuntos de relojes deben marcar a velocidades ligeramente diferentes, debido a sus diferentes movimientos (un efecto ya predicho por la relatividad especial) y sus diferentes posiciones dentro del campo gravitatorio de la Tierra. A fin de asegurar la precisi??n del sistema, los relojes de los sat??lites se ralentizado por un factor relativista, o ese mismo factor de se hace parte del algoritmo de evaluaci??n. A su vez, las pruebas de la precisi??n del sistema (sobre todo las medidas muy minuciosas que son parte de la definici??n de tiempo universal coordinado) son testimonio de la validez de las predicciones relativistas.
Un n??mero de otras pruebas han sondeado la validez de diferentes versiones de la principio de equivalencia; en rigor, todas las mediciones de la dilataci??n del tiempo gravitacional son pruebas de la versi??n d??bil de ese principio, no convierte por s?? la relatividad general. Hasta el momento, la relatividad general ha pasado todas las pruebas de observaci??n.
Aplicaciones Astrophysical
Los modelos basados en la relatividad general juegan un papel importante en la astrof??sica , y el ??xito de estos modelos es una prueba m??s de la validez de la teor??a.
La lente gravitatoria

Dado que la luz es desviada en un campo gravitacional, es posible que la luz de un objeto distante para llegar a un observador a lo largo de dos o m??s caminos. Por ejemplo, la luz de un objeto muy distante, como un quasar puede pasar a lo largo de un lado de una enorme galaxia y se desvi?? ligeramente con el fin de llegar a un observador en la Tierra, mientras que la luz que pasa a lo largo del lado opuesto de la misma galaxia es desviado, as??, alcanzar el mismo observador desde una direcci??n ligeramente diferente. Como resultado, ese observador particular, ver?? un objeto astron??mico en dos lugares diferentes en el cielo nocturno. Este tipo de enfoque es bien conocido cuando se trata de lentes ??pticas, y por lo tanto el efecto gravitacional correspondiente se llama lente gravitacional.
Astronom??a observacional utiliza efectos de lente como una herramienta importante para inferir propiedades del objeto-lente. Incluso en los casos en que ese objeto no es directamente visible, la forma de una imagen con lentes proporciona informaci??n sobre la masa de distribuci??n responsable de la desviaci??n de la luz. En particular, las lentes gravitacionales proporciona una forma de medir la distribuci??n de la materia oscura , que no emite luz y puede ser observado s??lo por sus efectos gravitatorios. Una aplicaci??n particularmente interesante son las observaciones a gran escala, donde las masas de lente se extienden sobre una fracci??n significativa del universo observable, y se puede utilizar para obtener informaci??n acerca de las propiedades a gran escala y evoluci??n de nuestro cosmos.
Las ondas gravitacionales
Las ondas gravitacionales, una consecuencia directa de la teor??a de Einstein, son distorsiones de la geometr??a que se propagan a la velocidad de la luz, y se pueden considerar como ondas en el espacio-tiempo. Ellos no deben confundirse con la ondas de gravedad de din??mica de fluidos, que son un concepto diferente.
Indirectamente, el efecto de las ondas gravitacionales se ha detectado en observaciones de estrellas binarias espec??ficas. Tales pares de estrellas orbitan entre s?? y, cuando lo hagan, perder??n gradualmente energ??a emitiendo ondas gravitatorias. Para las estrellas ordinarias como nuestro sol, esta pérdida de energía sería demasiado pequeño para ser detectable, pero esta pérdida de energía se observó en 1974 en un púlsar binario llamado PSR1913 + 16. En un sistema de este tipo, una de las estrellas que orbitan es un púlsar. Esto tiene dos consecuencias: un púlsar es un objeto extremadamente denso conocido como una estrella de neutrones, para el que la emisión de ondas gravitacionales es mucho más fuerte que las estrellas ordinarias. También, un púlsar emite un haz estrecho de radiación electromagnética de sus polos magnéticos. Al girar el púlsar, sus barridos del haz sobre la Tierra, donde se ve como una serie regular de pulsos de radio, así como un barco en el mar observa destellos regulares de la luz de la luz que gira en un faro. Este patrón regular de la radio pulsos funciona como un "reloj" de alta precisión. Se puede utilizar para medir el tiempo periodo orbital de la estrella doble, y reacciona con sensibilidad a las distorsiones del espacio-tiempo en su vecindad inmediata.
Los descubridores de PSR1913 + 16, Russell Hulse y Joseph Taylor, fueron galardonados con el Premio Nobel de Física en 1993. Desde entonces, se han encontrado varios otros púlsares binarios. Los más útiles son aquellas en las que ambas estrellas son púlsares, ya que proporcionan las pruebas más precisas de la relatividad general.
Actualmente, uno de los principales objetivos de la investigación en relatividad es la detección directa de ondas gravitacionales. Con este fin, una serie de terrestres detectores de ondas gravitacionales están en funcionamiento, y una misión para poner en marcha un detector basado en el espacio, LISA, se encuentra actualmente en fase de desarrollo, con una misión precursora ( LISA Pathfinder) debido para el lanzamiento en junio de 2013. Si se detectan ondas gravitacionales, que se podrían utilizar para obtener información acerca de los objetos compactos, como estrellas de neutrones y agujeros negros , y también para sondear el estado de los primeros universo fracciones de segundo después del Big Bang .
Agujeros negros

Cuando se concentra la masa en una suficientemente región compacta del espacio, la relatividad general predice la formación de un agujero negro - una región del espacio con una atracción gravitacional tan fuerte que ni siquiera la luz puede escapar. Ciertos tipos de agujeros negros se cree que son el estado final de la evolución de las grandes estrellas . Por otra parte, agujeros negros supermasivos con la masa de millones o miles de millones de Soles se supone que residen en los núcleos de la mayoría de las galaxias , y juegan un papel clave en la actual modelos de cómo las galaxias se han formado durante los últimos miles de millones de años.
La materia que cae sobre un objeto compacto es uno de los mecanismos más eficaces para la liberación de energía en forma de radiación y la materia que cae en los agujeros negros se cree que es responsable de algunos de los fenómenos astronómicos más brillantes imaginables. Ejemplos notables de gran interés para los astrónomos son los quásares y otros tipos de n??cleos gal??cticos activos. Bajo las condiciones adecuadas, la caída de la materia acumulando alrededor de un agujero negro puede conducir a la formación de chorros, en la que las vigas de la materia se centran lanzado hacia el espacio a velocidades cercanas a la de la luz .
Hay varias propiedades que lo hacen la mayoría de los agujeros negros fuentes prometedoras de ondas gravitacionales. Una de las razones es que los agujeros negros son los objetos más compactos que pueden orbitar entre sí como parte de un sistema binario; Como resultado, las ondas gravitacionales emitidas por un sistema de este tipo son especialmente fuertes. Otra razón se deduce de lo que se llaman teoremas singularidad del agujero negro: con el tiempo, los agujeros negros conservan sólo un conjunto mínimo de características distintivas (ya que diferentes estilos de cabello son una parte crucial de lo que da a diferentes personas sus diferentes apariencias, estos teoremas se han conocido como " sin pelo "teoremas). Por ejemplo, en el largo plazo, el colapso de un cubo materia hipotética no dar lugar a un agujero negro en forma de cubo. En cambio, el agujero negro resultante será indistinguible de un agujero negro formado por el colapso de una masa esférica, pero con una diferencia importante: en su transición a una forma esférica, el agujero negro formado por el colapso de un cubo emitirá ondas gravitacionales .
Cosmolog??a

Uno de los aspectos más importantes de la relatividad general es que puede aplicarse al universo como un todo. Un punto clave es que, a grandes escalas, nuestro universo parece estar construida a lo largo de líneas muy simples: todas las observaciones actuales sugieren que, en promedio, la estructura del cosmos debe ser aproximadamente la misma, independientemente de la ubicación o dirección de observación de un observador : el universo es aproximadamente homog??nea y isotr??pico. Tales universos relativamente simples pueden ser descritos por soluciones simples de las ecuaciones de Einstein. Los actuales modelos cosmológicos del universo se obtienen mediante la combinación de estas soluciones simples a la relatividad general con las teorías que describen las propiedades del universo de la materia de contenido, a saber, la termodinámica , nucleares y la física de partículas . Según estos modelos, nuestro universo actual surgió de un muy denso estado de alta temperatura (la Gran Explosión ) aproximadamente 14 bill??n años atrás, y ha estado expandiendo desde entonces.
Las ecuaciones de Einstein se puede generalizar añadiendo un término llamado constante cosmol??gica. Cuando este término está presente, en sí un espacio vacío actúa como una fuente de atractivo o, excepcionalmente, la gravedad repulsiva. Einstein introdujo originalmente este término en su artículo pionero 1917 sobre cosmología, con una motivación muy concreto: el pensamiento cosmológico contemporáneo sostuvo que el universo es estático, y se requirió el término adicional para construir universos modelo estático en el marco de la relatividad general. Cuando se hizo evidente que el universo no es estático, sino en expansión, Einstein se apresuró a desechar este plazo adicional; antes de tiempo, tal como lo conocemos hoy en día: Desde aproximadamente 1998 en adelante, un cuerpo acumulando constantemente de evidencia astronómica ha demostrado que la expansión del universo se está acelerando de una manera que sugiere la presencia de una constante cosmológica o, equivalentemente, de una energía oscura con la específica propiedades que impregna todo el espacio.
La investigación moderna: la relatividad general y más allá
La relatividad general es un gran éxito en la prestación de un marco de modelos precisos que describen una impresionante variedad de fenómenos físicos. Por otra parte, hay muchas preguntas abiertas interesantes y, en particular, la teoría en su conjunto es casi ciertamente incompleta.
A diferencia de todas las demás teorías modernas de las interacciones fundamentales, la relatividad general es una teoría clásica: no incluye los efectos de la física cuántica . La búsqueda de una versión cuántica de la relatividad general se dirige a uno de los más fundamentales preguntas abiertas en la física. Si bien no son candidatos prometedores para una teoría de tal gravedad cuántica, en particular la teoría de cuerdas y la gravedad cuántica de bucles, en la actualidad hay una teoría coherente y completa. Desde hace tiempo se esperaba que una teoría de la gravedad cuántica también eliminaría otra característica problemática de la relatividad general: la presencia de singularidades espacio-tiempo. Estas singularidades son los límites ("filos") de espacio-tiempo en el que se convierte en mal definida la geometría, con la consecuencia de que la propia relatividad general pierde su poder predictivo. Además, existen los llamados teoremas de singularidad que predicen que tales singularidades deben existir en el universo, si las leyes de la relatividad general iban a celebrar sin ninguna modificación cuántica. Los ejemplos más conocidos son las singularidades asociadas a los universos modelo que describen los agujeros negros y el origen del universo .
Otros intentos de modificar la relatividad general se han hecho en el contexto de la cosmología . En los modelos cosmológicos modernos, la mayor parte de la energía en el universo es en formas que nunca han sido detectadas directamente, es decir, la energía oscura y la materia oscura . Ha habido varias propuestas controversiales para obviar la necesidad de estas formas enigmáticas de la materia y la energía, mediante la modificación de las leyes que rigen la gravedad y la dinámica de la expansión cósmica, por ejemplo modificado la dinámica newtoniana.
Más allá de los retos de los efectos cuánticos y la cosmología, la investigación sobre la relatividad general es rico en posibilidades para una mayor exploración: relativistas matemáticos exploran la naturaleza de las singularidades y las propiedades fundamentales de las ecuaciones de Einstein, simulaciones por ordenador cada vez más amplios de espacio-tiempos específicos (como los que describen la fusión agujeros negros) se ejecutan, y la carrera por la primera detección directa de ondas gravitacionales continúa a buen ritmo. Más de noventa años después de la teoría fue publicada por primera vez, la investigación es más activa que nunca.