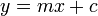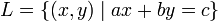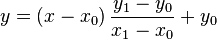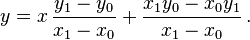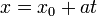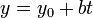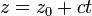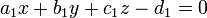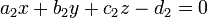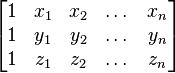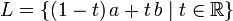Line (geometría)

Tres líneas - las líneas rojas y azules tienen la misma pendiente, mientras que los rojos y verdes tienen el mismo punto de intersección.

Una representación de una segmento de línea

Geometría
Oxirrinco papiro (P.Oxy. I 29) que muestra un fragmento de los Elementos de Euclides
Historia de la geometría
Ramas Geometría euclidiana · La geometría no-euclidiana · Geometría analítica · La geometría de Riemann · Geometría diferencial · La geometría descriptiva · La geometría algebraica
Líneas de investigación La geometría algebraica · Geometría diferencial · Geometría simpléctica
Conceptos importantes Notas · · Línea Perpendicular · Paralelo · El segmento de línea · Ray · Plano · Longitud · Espacio · Volumen · Vertex · ángulo · Congruencia · Similitud · Polígono · Triángulo · Altitud · Hipotenusa · teorema de Pitágoras · Cuadrilátero · Trapecio · Kite · Paralelogramo ( Romboidal, Rectángulo, Rombo, Plaza ) · Diagonal · Simetría · curva · Círculo · Área de un círculo · Circunferencia · Diámetro · Cilindro · Esfera · Pirámide · Dimensiones ( uno, dos, tres, cuatro)
Los geómetras Aryabhata · Ahmes · Apolonio · Arquímedes · Baudhayana · Bolyai · Brahmagupta · Euclides · Pitágoras · Khayyám · Descartes · Pascal · Euler · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · Katyayana · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · Poincaré · Sijzi · Hilbert · Minkowski · Cartan · Veblen · Sakabe Kohan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng

La noción de línea o línea recta fue introducido por los matemáticos antiguos para representar objetos rectas con anchura y profundidad insignificante. Las líneas son una idealización de tales objetos. Por lo tanto, hasta el siglo XVII, las líneas se definieron así: "La línea es la primera especie de la cantidad, que tiene sólo una dimensión, es decir, la longitud, sin ningún tipo de anchura ni la profundidad, y no es otra cosa que el flujo o de ejecución del punto que [...] Saldremos desde su imaginario moviendo algún vestigio de longitud, exentos de cualquier anchura. [...] La línea recta es la que se extiende por igual entre sus puntos "

Euclides describe una línea como "longitud sin anchura", y presentó varios postulados indemostrables como propiedades básicas de la que construye la geometría, que ahora se llama la geometría euclidiana para evitar confusiones con otras geometrías que se han introducido desde el fin del siglo XIX (como geometría no euclidiana, la geometría proyectiva, y geometría afín).

En la matemática moderna, dada la multitud de geometrías, el concepto de una línea está estrechamente ligada a la forma en que la geometría se describe. Por ejemplo, en la geometría analítica , una línea en el plano se define a menudo como el conjunto de puntos cuyas coordenadas satisfacer una determinada ecuación lineal , pero en un entorno más abstracto, tales como la geometría de la incidencia, una línea puede ser un objeto independiente, distinto del conjunto de puntos que se encuentran en él.

Cuando una geometría se describe mediante un conjunto de axiomas, la noción de una línea por lo general se dejan sin definir (a la llamada objeto primitivo). Las propiedades de las líneas A continuación se determinan por los axiomas que se refieren a ellos. Una ventaja de este enfoque es la flexibilidad que da a los usuarios de la geometría. Así, en la geometría diferencial de una línea puede ser interpretado como un geodésica (camino más corto entre dos puntos), mientras que en algunos geometrías proyectivas una línea es un espacio vectorial de 2 dimensiones (todas las combinaciones lineales de dos vectores independientes). Esta flexibilidad también se extiende más allá de las matemáticas y, por ejemplo, permite a los físicos a pensar en la trayectoria de un rayo de luz como una línea.

La segmento de línea es una parte de una línea que está delimitada por dos puntos finales distintos y contiene todos los puntos en la línea entre sus puntos extremos. Dependiendo de cómo se define el segmento de línea, cualquiera de los dos puntos finales pueden o no ser parte del segmento de línea. Dos o más segmentos de línea pueden tener algunas de las mismas relaciones como líneas, como paralelas, se cruzan, o sesgar.

Definiciones frente a las descripciones

Todas las definiciones son en última instancia, de naturaleza circular ya que dependen de conceptos que deben ellos mismos tienen definiciones, una dependencia que no se puede continuar indefinidamente sin volver al punto de partida. Para evitar este círculo vicioso ciertos conceptos deben ser tomados como conceptos primitivos; términos que se dan ninguna definición. En la geometría, es con frecuencia el caso de que el concepto de la línea se toma como una primitiva. En aquellas situaciones en las que una línea es un concepto definido, como en la geometría de coordenadas , algunas otras ideas fundamentales se toman como primitivas. Cuando el concepto de línea es una primitiva, el comportamiento y las propiedades de las líneas son dictadas por el axiomas que deben satisfacer.

En un tratamiento axiomático no axiomática o simplificada de la geometría, el concepto de una noción primitiva puede ser demasiado abstracto para ser tratado. En este caso es posible que se proporciona una descripción o imagen mental de una noción primitiva para dar una base para construir la noción de que formalmente se basa en los axiomas (no declaradas). Las descripciones de este tipo pueden ser referidos a, por algunos autores, como definiciones de este estilo informal de presentación. Estas no son las definiciones verdaderas y no podían utilizarse en pruebas formales de los estados. La "definición" de la línea en los Elementos de Euclides entra en esta categoría. Incluso en el caso en que se está considerando una geometría específica (por ejemplo, la geometría euclidiana ), hay un acuerdo generalmente aceptada entre los autores en cuanto a lo que una descripción informal de una línea debe ser cuando el sujeto no está siendo tratado formalmente.

Geometría euclidiana

Cuando la geometría se formalizó por primera vez por Euclides en Elementos , definió una línea de ser "longitud sin anchura" con una línea recta es una línea ", que yace por igual respecto de los puntos sobre sí mismo". Estas definiciones sirven de poco ya que utilizan términos que no son, ellos mismos, definen. De hecho, Euclides no hizo uso de estas definiciones en este trabajo y, probablemente, los incluyó sólo para dejar claro al lector lo que se estaba discutiendo. En la geometría moderna, una línea se toma simplemente como un objeto indefinido con propiedades dadas por axiomas, pero a veces se define como un conjunto de puntos que obedecen a una relación lineal cuando algún otro concepto fundamental se deja indefinido.

En una formulación axiomático de la geometría euclidiana, como la de Hilbert (axiomas originales de Euclides contenían diversas fallas que han sido corregidas por los matemáticos modernos), una línea se afirma que tienen ciertas propiedades que se refieren a otras líneas y puntos. Por ejemplo, para dos puntos distintos, hay una línea única que contiene ellos, y cualquiera de las dos líneas distintas se cruzan en un solo punto. En dos dimensiones, es decir, la euclidiana plano , dos líneas que no se intersecan se llaman paralelo. En las dimensiones superiores, dos líneas que no se cruzan pueden ser paralelas si están contenidos en un avión , o sesgar si no lo son.

Cualquier colección de un número finito de líneas divide el plano en polígonos convexos (posiblemente sin límites); Esta partición se conoce como una disposición de las líneas.

Rayo

Dada una línea y un punto cualquiera en él, podemos considerar como una descomposición de esta línea en dos partes. Cada uno de tales parte se llama un rayo (o medio-line) y el punto A se llama su punto inicial. El punto A se considera que es un miembro del rayo. Intuitivamente, un rayo consiste en esos puntos en una recta que pasa por A y que proceden de forma indefinida, a partir de A, sólo en una dirección a lo largo de la línea. Sin embargo, con el fin de utilizar este concepto de un rayo en las pruebas se requiere una definición más precisa.

Dada puntos distintos A y B, que determinan un rayo único con el punto inicial A. Como dos puntos definen una línea única, este rayo consiste en todos los puntos entre A y B (incluyendo A y B) y todos los puntos C en la línea a través de A y B tal que B está entre A y C. Esto es, a veces, también expresó como el conjunto de todos los puntos de C tal que A no es entre B y C. Un punto D, en la línea determinada por A y B, pero no en el rayo con el punto inicial A determinado por B, determinará otro rayo con el punto inicial A. Con respecto al rayo AB, el rayo AD se llama el rayo opuesto.

Por lo tanto, podríamos decir que dos puntos diferentes, A y B, definen una línea y una descomposición de esta línea en el unión de la desunión de un segmento abierto (A, B) y dos rayos, AC y AD (el punto D no se dibuja en el diagrama, pero está a la izquierda de A en la línea AB). Estos no son rayos opuestos, ya que tienen diferentes puntos iniciales.

La definición de un rayo depende de la noción de intermediación de puntos en una línea. De ello se desprende que existen rayos sólo para geometrías para los que existe esta noción, por lo general la geometría euclidiana o geometría afín a través de una campo ordenado. Por otro lado, no existen rayos en geometría proyectiva ni en una geometría sobre un no campo ordenado, como los números complejos o cualquier campo finito.

En topología , un rayo en un espacio X es una incrustación continua R ⁺ → X. Se utiliza para definir el concepto importante de extremo del espacio.

Geometría de coordenadas

En la geometría de coordenadas , líneas en un plano cartesiano pueden ser descritos por algebraicamente ecuaciones lineales . En dos dimensiones, la ecuación para líneas no verticales se da a menudo en la forma pendiente-intersección :

donde:

m es el pendiente o pendiente de la recta.

c es la intersección y de la línea.

x es el variable independiente de la función y = f (x).

La pendiente de la recta que pasa por los puntos A (x _a, y _a) y B (x _b, y _b), cuando X _a ≠ x _b, está dada por m = (y _b -y _a) / _(b x -x _a) y la ecuación de esta línea se puede escribir y = m (x - x _a) + y _a.

En R ^2, cada línea L (incluyendo las líneas verticales) se describe mediante una ecuación lineal de la forma

con verdadera fijo coeficientes a, b y c de tal manera que A y B no sean ambos cero. El uso de este forma, líneas verticales corresponden a las ecuaciones con b = 0.

Hay muchas maneras de variantes para escribir la ecuación de una línea de la que todos se pueden convertir de una a otra mediante la manipulación algebraica. Estas formas (ver ecuación lineal para otras formas) son generalmente nombrados por el tipo de información (datos) sobre la línea que se necesita para escribir la forma. Algunos de los datos importantes de una línea es su pendiente, intersección x, puntos conocidos de la línea y la intersección.

La ecuación de la línea que pasa a través de dos puntos diferentes 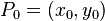y 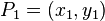puede ser escrito como

.

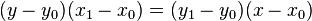Si x ≠ ₀ x _1, esta ecuación puede ser reescrita como

o

En tres dimensiones, las líneas no pueden ser descritos por una única ecuación lineal, por lo que con frecuencia se describen por ecuaciones paramétricas:

donde:

x, y, y z son todas las funciones del t variable independiente que se extiende sobre los números reales.

(X _0, y _0, z ₀₎ es cualquier punto de la línea.

a, b, y c están relacionadas con la pendiente de la línea, de manera que el vector (a, b, c) es paralela a la línea.

También se pueden describir como las soluciones simultáneas de dos ecuaciones lineales

de tal manera que 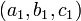y 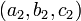no son proporcionales (las relaciones 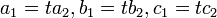implicar t = 0). Esto se deduce ya que en tres dimensiones una sola ecuación lineal típicamente describe un avión y una línea es lo que es común a dos planos que se cortan distintas.

Ecuación vectorial

La ecuación vectorial de la línea a través de los puntos A y B está dado por r = OA + λ AB (donde λ es un escalar).

Si a es vector OA y OB vector b es, entonces la ecuación de la línea se puede escribir: r = a + λ (b - a).

Un rayo comenzando en el punto A se describe mediante la limitación de λ. Se obtiene un rayo si λ ≥ 0, y el rayo opuesto viene de λ ≤ 0.

Puntos colineales

Tres puntos se dice que son colineales si se encuentran en la misma línea. En el espacio euclidiano , tres puntos por lo general determinan un plano , pero en el caso de tres puntos alineados esto no sucede.

En la geometría analítica , n-dimensional espacio los puntos X = (x _1, x _2, ..., x _n), Y = (y _1, y _2, ..., y _n), y Z = (z _1, z _2, ..., z _n) son colineales si la matriz

tiene un clasificar menos de 3. En particular, para los tres puntos en el plano (n = 2), por encima de la matriz es cuadrada y los puntos son colineales si y sólo si su determinante es cero.

Cuando la distancia d (a, b) entre dos puntos A y B se define, la colinealidad entre tres puntos se puede expresar a través de:

Los puntos a, b y c son colineales si y sólo si d (x, a) = d (c, a) y d (x, b) = d (c, b) implica x = c.

En la geometría euclidiana esta propiedad es cierto, ya que si c no está en la línea determinada por ayb habrá otro punto (no es igual a c), que es igual de lejos de a y b como el punto c es (visualizar el punto en el otro lado de la línea que es la imagen especular de c).

En las geometrías donde el concepto de una línea es un noción primitiva, como puede ser el caso en algunos geometrías sintéticas, se necesitan otros métodos para determinar la colinealidad.

Espacio euclidiano

En el espacio euclidiano , R ⁿ (y de forma análoga en todos los demás espacio afín), la línea L que pasa por dos puntos A y B (considerado como vectores) es el subconjunto

La dirección de la línea es de un (t = 0) a B (t = 1), o en otras palabras, en la dirección del vector b - a. Diferentes opciones de ayb pueden producir la misma línea.

Tipos de líneas

En cierto sentido, todas las líneas de la geometría euclidiana son iguales, ya que, sin coordenadas, uno no puede distinguirlos unos de otros. Sin embargo, las líneas pueden desempeñar funciones especiales con respecto a otros objetos de la geometría y se divide en tipos de acuerdo con esa relación. Por ejemplo, con respecto a una cónica , las líneas pueden ser:

• Líneas tangentes ,
• Líneas secantes,
• Líneas del exterior, que no cumplen con la cónica en cualquier punto del plano euclidiano, o una más especializada
• directriz .

Para más general curvas algebraicas, las líneas también podrían ser:

• i -secant líneas, cumpliendo la curva en los puntos i contado sin la multiplicidad, o
• asíntotas.

Con respecto a los triángulos tenemos:

• la Recta de Euler, y
• la Líneas de Simson.

Para un hexágono con vértices acostado en una cónica tenemos la Línea de Pascal y, en el caso especial en que la cónica es un par de líneas, tenemos la Línea de Pappus.

Geometría proyectiva

En muchos modelos de la geometría proyectiva, la representación de una línea rara vez se ajusta a la noción de la "curva de recta", como se visualiza en la geometría euclidiana. En Geometría elíptica vemos un ejemplo típico de esto. En la representación esférica de la geometría elíptica, están representados por líneas grandes círculos de una esfera con puntos diametralmente opuestos identificados. En un modelo diferente de la geometría elíptica, están representados por líneas euclidianas planos que pasan por el origen. A pesar de que estas representaciones son visualmente distintas, satisfacen todas las propiedades (como, dos puntos determinan una línea única) que los hacen representaciones adecuadas para líneas en esta geometría.

Geodesia

La "rectitud" de una línea, interpretado como la propiedad que minimiza las distancias entre sus puntos, se puede generalizar y nos lleva al concepto de geodésicas en espacios métricos.