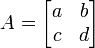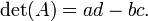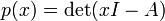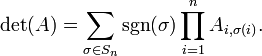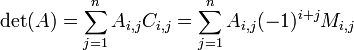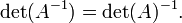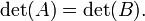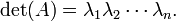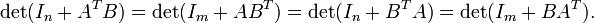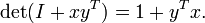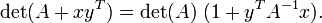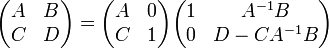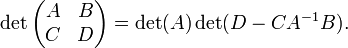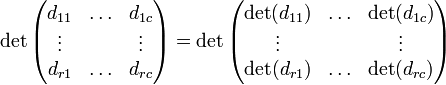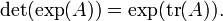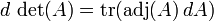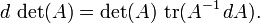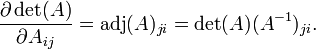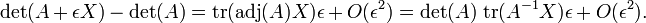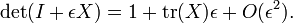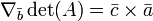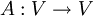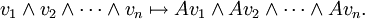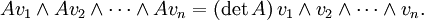Determinante
Sab??as ...
La organizaci??n de una selecci??n de Wikipedia para escuelas en el mundo en desarrollo sin internet fue una iniciativa de SOS Children. patrocinio SOS Ni??o est?? genial!
En ??lgebra , un factor determinante es una funci??n dependiente de n que asocia un escalar, det (A), para cada n ?? n matriz cuadrada A. El significado geom??trico fundamental de un determinante es como la factor de escala para el volumen cuando A es considerado como una transformaci??n lineal. Determinantes son importantes tanto en el c??lculo , donde entran en el regla de sustituci??n de varias variables, y en ??lgebra multilineal.
Para un n??mero entero positivo n fijo, hay una funci??n determinante ??nico para el n ?? n matrices sobre cualquier anillo conmutativo R. En particular, existe esta funci??n cuando R es el campo de reales o n??meros complejos .
Notaci??n barra vertical
El determinante de una matriz A veces tambi??n se denota por | A |. Esta notaci??n puede ser ambigua, ya que tambi??n se utiliza para ciertas normas de la matriz y para el valor absoluto . Sin embargo, a menudo la norma matriz se denota con barras verticales dobles (por ejemplo, ‖ ‖ A) y puede llevar a un sub??ndice tambi??n. Por lo tanto, la notaci??n barra vertical para determinante se utiliza con frecuencia (por ejemplo, La regla de Cramer y menores de edad). Por ejemplo, para la matriz
el determinante 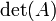 podr??a ser indicado por
podr??a ser indicado por  o m??s expl??citamente como
o m??s expl??citamente como
Es decir, los corchetes alrededor de las matrices se sustituyen con barras verticales alargadas.
Determinantes de matrices 2-por-2

La matriz 2 ?? 2
tiene determinante
La interpretaci??n cuando la matriz tiene entradas de n??meros reales es que esto da el ??rea orientada de la paralelogramo con v??rtices en (0,0), (a, b), (a + c, b + d), y (c, d). La zona orientada es el mismo que el habitual zona , excepto que es negativa cuando los v??rtices se enumeran en orden las agujas del reloj.
El supuesto aqu?? es que la transformaci??n lineal se aplica a la fila vectores como el producto vectorial de matriz 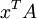 , Donde
, Donde 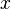 es un vector columna. El paralelogramo en la figura se obtiene multiplicando los vectores fila
es un vector columna. El paralelogramo en la figura se obtiene multiplicando los vectores fila  y
y  , La definici??n de los v??rtices del cuadrado de la unidad. Con el producto matriz-vector m??s com??n
, La definici??n de los v??rtices del cuadrado de la unidad. Con el producto matriz-vector m??s com??n  el paralelogramo tiene v??rtices en
el paralelogramo tiene v??rtices en  y
y  (Tenga en cuenta que
(Tenga en cuenta que  ).
).
Se dar?? a continuaci??n una f??rmula para matrices m??s grandes.
Determinantes de matrices 3-por-3

La matriz 3 ?? 3:
Usando el expansi??n cofactor en la primera fila de la matriz se obtiene:

que puede ser recordado como la suma de los productos de tres diagonal noroeste de l??neas al sur-este de elementos de la matriz, menos la suma de los productos de tres diagonal suroeste de l??neas al noreste de elementos cuando las copias de la primera dos columnas de la matriz se escriben junto a ??l como a continuaci??n:
Tenga en cuenta que esta regla mnemot??cnica no se traslada en dimensiones superiores.
Aplicaciones
Determinantes se utilizan para caracterizar matrices invertibles (es decir, exactamente esas matrices con determinantes distintos de cero), y para describir expl??citamente la soluci??n de un sistema de ecuaciones lineales con La regla de Cramer. Se pueden utilizar para encontrar los valores propios de la matriz  a trav??s de polinomio caracter??stico
a trav??s de polinomio caracter??stico
donde I es la matriz de identidad de la misma dimensi??n que A.
Se piensa a menudo del determinante como la asignaci??n de un n??mero a cada secuencia de 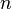 vectores en
vectores en 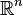 , Mediante el uso de la matriz cuadrada cuyas columnas son los vectores dados. Con este entendimiento, el signo del determinante de una base se puede utilizar para definir la noci??n de orientaci??n en espacios eucl??deos . El determinante de un conjunto de vectores es positivo si forman los vectores de un diestro sistema de coordenadas, y negativo si zurdo.
, Mediante el uso de la matriz cuadrada cuyas columnas son los vectores dados. Con este entendimiento, el signo del determinante de una base se puede utilizar para definir la noci??n de orientaci??n en espacios eucl??deos . El determinante de un conjunto de vectores es positivo si forman los vectores de un diestro sistema de coordenadas, y negativo si zurdo.
Determinantes se utilizan para calcular los vol??menes de c??lculo de vectores : el valor absoluto del determinante de vectores reales es igual al volumen de la paralelep??pedo atravesado por aquellos vectores. Como consecuencia, si el mapa lineal 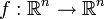 est?? representado por la matriz
est?? representado por la matriz  Y
Y 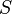 es cualquiera medible subconjunto de
es cualquiera medible subconjunto de 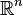 , Entonces el volumen de
, Entonces el volumen de  es dado por
es dado por 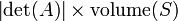 . M??s generalmente, si el mapa lineal
. M??s generalmente, si el mapa lineal 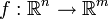 est?? representado por la
est?? representado por la 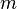 -by-
-by- 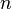 matriz
matriz  Y
Y 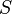 es cualquier subconjunto medible de
es cualquier subconjunto medible de 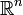 , Entonces el
, Entonces el 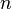 - volumen dimensional de
- volumen dimensional de  es dado por
es dado por  . Al calcular el volumen del tetraedro delimitada por cuatro puntos, que pueden ser utilizados para identificar l??neas oblicuas.
. Al calcular el volumen del tetraedro delimitada por cuatro puntos, que pueden ser utilizados para identificar l??neas oblicuas.
El volumen de cualquier tetraedro , dado sus v??rtices a, b, c, y d, es (1/6) ?? | det (a - b, b - c, c - d) |, o cualquier otra combinaci??n de pares de v??rtices que forma un simplemente conectado gr??fico.
Definici??n general y la computaci??n
La definici??n del determinante viene de la siguiente teorema.
Teorema. Sea M n (K) denota el conjunto de todos 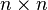 matrices sobre el campo K. Existe exactamente una funci??n
matrices sobre el campo K. Existe exactamente una funci??n
con las dos propiedades:
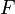 es alterno multilineal con respecto a las columnas;
es alterno multilineal con respecto a las columnas; 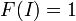 .
.
Uno puede entonces definir el determinante como la funci??n ??nica con las propiedades anteriores.
Para probar el teorema anterior, tambi??n se obtiene la F??rmula de Leibniz:
Aqu?? la suma se calcula sobre todas las permutaciones 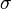 de los n??meros de {1,2, ..., n} y
de los n??meros de {1,2, ..., n} y  denota la firma de la permutaci??n
denota la firma de la permutaci??n 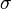 : 1 si
: 1 si 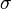 es una incluso permutaci??n y -1 si es impar.
es una incluso permutaci??n y -1 si es impar.
Esta f??rmula contiene 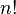 ( factorial ) sumandos, y es por lo tanto poco pr??ctico utilizar para calcular determinantes para grandes
( factorial ) sumandos, y es por lo tanto poco pr??ctico utilizar para calcular determinantes para grandes 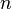 .
.
Para las peque??as matrices, se obtiene las siguientes f??rmulas:
- si
 es una matriz de 1 por 1, a continuaci??n,
es una matriz de 1 por 1, a continuaci??n, 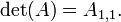
- si
 es una matriz de 2 por 2, a continuaci??n,
es una matriz de 2 por 2, a continuaci??n, 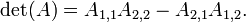
- para una matriz de 3 por 3
 , La f??rmula es m??s complicado:
, La f??rmula es m??s complicado:
que toma la forma del esquema Sarrus ' .
En general, los factores determinantes se pueden calcular utilizando la eliminaci??n gaussiana usando las siguientes reglas:
- Si
 es un matriz triangular, es decir,
es un matriz triangular, es decir, 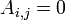 siempre que
siempre que 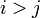 o, alternativamente, cada vez
o, alternativamente, cada vez 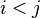 , A continuaci??n,
, A continuaci??n,  (El producto de las entradas diagonales de
(El producto de las entradas diagonales de  ).
). - Si
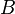 resultados de
resultados de  mediante el intercambio de dos filas o columnas, entonces
mediante el intercambio de dos filas o columnas, entonces 
- Si
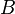 resultados de
resultados de  multiplicando una fila o columna con el n??mero de
multiplicando una fila o columna con el n??mero de  , A continuaci??n,
, A continuaci??n, 
- Si
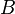 resultados de
resultados de  mediante la adici??n de un m??ltiplo de una fila a otra fila, o un m??ltiplo de una columna a otra columna, a continuaci??n,
mediante la adici??n de un m??ltiplo de una fila a otra fila, o un m??ltiplo de una columna a otra columna, a continuaci??n, 
Expl??citamente, comenzando con alguna matriz, utilizar los ??ltimos tres reglas para convertirlo en una matriz triangular, a continuaci??n, utilizar la primera regla para calcular su determinante.
Tambi??n es posible ampliar un determinante a lo largo de una fila o columna usando La f??rmula de Laplace, que es eficiente para matrices relativamente peque??as. Para ello a lo largo de la fila 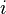 , Por ejemplo, escribimos
, Por ejemplo, escribimos
donde el 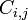 representar la matriz cofactores, es decir,
representar la matriz cofactores, es decir, 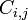 es
es  veces el menor
veces el menor  , Que es el determinante de la matriz que resulta de
, Que es el determinante de la matriz que resulta de  mediante la eliminaci??n de la
mediante la eliminaci??n de la 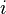 fila -??simo y la
fila -??simo y la 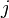 columna -th.
columna -th.
Ejemplo
Supongamos que queremos calcular el determinante de
Podemos seguir adelante y utilizar la f??rmula de Leibniz directamente:
- Click on the following link to visit or download this HTML page
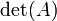

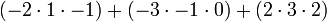



Alternativamente, podemos utilizar La f??rmula de Laplace para ampliar el determinante a lo largo de una fila o columna. Lo mejor es elegir una fila o columna con muchos ceros, por lo que se expandir?? a lo largo de la segunda columna:
- Click on the following link to visit or download this HTML page

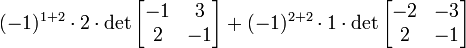


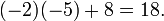
Una tercera forma (y el m??todo de elecci??n para matrices m??s grandes) implicar??an el algoritmo de Gauss. Al hacer los c??lculos a mano, a menudo se puede acortar cosas dram??ticamente a??adiendo inteligentemente m??ltiplos de columnas o filas a otras columnas o filas; esto no cambia el valor del determinante, pero puede crear entradas de cero lo que simplifica los c??lculos posteriores. En este ejemplo, la adici??n de la segunda columna a la primera uno es especialmente ??til:
y este determinante puede ser expandido r??pidamente a lo largo de la primera columna:
- Click on the following link to visit or download this HTML page
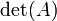



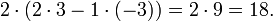
Propiedades
El determinante es un mapa multiplicativo en el sentido de que
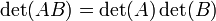 para todo n -by- n matrices
para todo n -by- n matrices  y
y 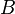 .
.
Esto se generaliza por el F??rmula de Cauchy-Binet a los productos de matrices no cuadradas.
Es f??cil ver que 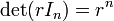 y por lo tanto
y por lo tanto
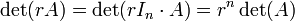 para todos
para todos 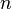 -by-
-by- 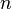 matrices
matrices  y todo escalares
y todo escalares  .
.
Una matriz sobre un anillo conmutativo R es invertible si y s??lo si su determinante es una unidad en R. En particular, si A es una matriz sobre una campo como los reales o n??meros complejos , entonces A es invertible si y s??lo si det (A) no es cero. En este caso tenemos
Expresado de otra manera: los vectores v 1, ..., v n en R n forman un base si y s??lo si det (v 1, ..., v n) es distinto de cero.
Una matriz y su transponer tienen el mismo determinante:
Los determinantes de una matriz compleja y de su transpuesta conjugada son conjugado:
(Tenga en cuenta la transpuesta conjugada es id??ntica a la transposici??n de una matriz real)
El determinante de una matriz  exhibe las siguientes propiedades bajo transformaciones matriciales elementales de
exhibe las siguientes propiedades bajo transformaciones matriciales elementales de  :
:
- Intercambiar filas o columnas multiplica el determinante por -1.
- Multiplicar una fila o columna
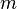 multiplica por el factor determinante
multiplica por el factor determinante 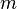 .
. - Adici??n de un m??ltiplo de una fila o columna a otra deja el determinante sin cambios.
As?? se desprende de la propiedad multiplicativa y los determinantes de la elementales matrices de transformaci??n de la matriz.
Si  y
y 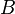 son similar, es decir, si existe una matriz invertible
son similar, es decir, si existe una matriz invertible 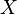 de tal manera que
de tal manera que  =
= 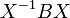 , Y luego por la propiedad multiplicativa,
, Y luego por la propiedad multiplicativa,
Esto significa que el determinante es una similitud invariante. Debido a esto, el determinante de alguna transformaci??n lineal T: V → V para algunos de dimensi??n finita espacio vectorial V es independiente de la base de la V. La relaci??n es de un solo sentido, sin embargo: existen matrices que tienen el mismo determinante, pero no son similares.
Si  es un cuadrado
es un cuadrado 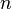 -by-
-by- 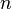 matriz con reales o complejos entradas y si λ 1, ..., λ n son los (complejo) valores propios de
matriz con reales o complejos entradas y si λ 1, ..., λ n son los (complejo) valores propios de  enumerados seg??n sus multiplicidades algebraicas, luego
enumerados seg??n sus multiplicidades algebraicas, luego
Esto se deduce del hecho de que  siempre es similar a su Jordan forma normal, una matriz triangular superior con los valores propios de la diagonal principal.
siempre es similar a su Jordan forma normal, una matriz triangular superior con los valores propios de la diagonal principal.
Identidades ??tiles
Para m -by- n matriz A y m -by- n matriz B, se tiene
Una consecuencia de estas igualdades para el caso de (columna) vectores x e y
Y una versi??n generalizada de esta identidad
Las pruebas se pueden encontrar en .
Matrices Bloque
Supongamos,  son
son  matrices respectivamente. Entonces
matrices respectivamente. Entonces
Esto puede ser (bastante) f??cilmente visto desde por ejemplo la F??rmula de Leibniz. Empleando la siguiente identidad
lleva a
Identidad similares con  factorizada a cabo se puede derivar de forma an??loga. Estas identidades se tomaron de .
factorizada a cabo se puede derivar de forma an??loga. Estas identidades se tomaron de .
Si 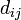 son matrices diagonales, entonces
son matrices diagonales, entonces
Este es un caso especial del teorema publicado en .
Relaci??n con el rastro
A partir de esta conexi??n entre el determinante y los valores propios, se puede derivar una conexi??n entre el funci??n de rastreo, la funci??n exponencial, y el determinante:
Realizar la sustituci??n 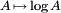 en los rendimientos de ecuaciones anteriores
en los rendimientos de ecuaciones anteriores
que est?? estrechamente relacionado con el Determinante Fredholm. Del mismo modo,
Para n -by- n matrices est??n las relaciones:
- Caso n = 1:
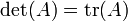
- Caso n = 2:

- Caso n = 3:

- Caso n = 4:

que est??n estrechamente relacionados con Identidades de Newton.
Derivado
El determinante de matrices cuadradas reales es una funci??n polin??mica de 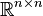 a
a 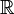 , Y como tal, est?? en todas partes diferenciables . Su derivado puede expresarse utilizando La f??rmula de Jacobi:
, Y como tal, est?? en todas partes diferenciables . Su derivado puede expresarse utilizando La f??rmula de Jacobi:
donde adj (A) denota la adjugate de A. En particular, si A es invertible, tenemos
En forma de componentes, estos son
Cuando  es un peque??o n??mero de ??stos son equivalentes a
es un peque??o n??mero de ??stos son equivalentes a
El caso especial de que  es igual a la matriz identidad
es igual a la matriz identidad 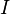 rendimientos
rendimientos
Una propiedad ??til en el caso de 3 x 3 matrices es la siguiente:
A puede escribirse como 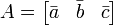 donde
donde  ,
, 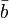 ,
,  son vectores, entonces el gradiente de m??s de uno de los tres vectores se puede escribir como el producto cruzado de los otros dos:
son vectores, entonces el gradiente de m??s de uno de los tres vectores se puede escribir como el producto cruzado de los otros dos:
Formulaci??n abstracta
Un n ?? n matriz cuadrada A puede ser pensado como la representaci??n de una coordenada transformaci??n lineal de un n-dimensional espacio vectorial V. Dado cualquier transformaci??n lineal
podemos definir el determinante de A como el determinante de cualquier representaci??n matricial de A. Esto es un noci??n bien definida (es decir, independiente de la elecci??n de base), ya que el determinante es invariante bajo transformaciones de semejanza.
Como era de esperar, es posible definir el determinante de una transformaci??n lineal de manera coordinar libre. Si V es un espacio vectorial n-dimensional, entonces uno puede construir su cima exterior Λ potencia n V. Este es un espacio vectorial unidimensional cuyos elementos est??n escritos
donde cada v i es un vector en V y la producto exterior ∧ es antisim??trica (es decir, u ∧ u = 0). Cualquier transformaci??n lineal A: V → V induce una transformaci??n lineal de Λ n V de la siguiente manera:
Desde Λ V n es unidimensional esta operaci??n se acaba de multiplicaci??n por algunos escalar que depende de una. Esta escalar se llama el determinante de A. Es decir, definimos det (A) por la ecuaci??n
Se puede comprobar que esta definici??n est?? de acuerdo con la definici??n de coordenadas dependiente dado anteriormente.
Aplicaci??n algor??tmica
- El m??todo ingenua de la aplicaci??n de un algoritmo para calcular el determinante es el uso de la f??rmula de Laplace para la expansi??n por cofactores. Este enfoque es extremadamente ineficiente en general, sin embargo, ya que es de orden n! (N factorial ) para una matriz n ?? n M.
- Una mejora de orden n 3 se puede lograr mediante el uso de Descomposici??n LU escribir M = LU para triangular matrices L y U. Ahora, det M = det LU = det L det U, y desde L y U son triangulares el determinante de cada uno es simplemente el producto de sus elementos diagonales. Alternativamente, se puede realizar la Descomposici??n de Cholesky si es posible o la Descomposici??n QR y encontrar el determinante de una manera similar.
- Dado que la definici??n del determinante no necesita divisiones, surge una pregunta: ??algoritmos r??pidos existir que no necesitan divisiones? Esto es especialmente interesante para las matrices sobre anillos. Algoritmos hecho con tiempo de ejecuci??n proporcional an 4 existir. Una algoritmo de Mahajan y Vinay, y Berkowitz se basa en caminatas ordenadas cerrados (corto Clow). Se calcula m??s productos que la definici??n determinante requiere, pero algunos de estos productos cancelar y la suma de estos productos se puede calcular de manera m??s eficiente. El algoritmo final se parece mucho a un producto iterativa de las matrices triangulares.
- Lo que no se discute a menudo es el llamado "complejidad poco" del problema, es decir, la cantidad de bits de precisi??n que necesita para almacenar los valores intermedios. Por ejemplo, usando eliminaci??n de Gauss , se puede reducir la matriz a la forma triangular superior, luego multiplicar la diagonal principal de obtener el determinante (este es esencialmente un caso especial de la descomposici??n LU como antes), pero un c??lculo r??pido mostrar?? que el bit tama??o de valores intermedios potencialmente podr??a llegar a ser exponencial. Se podr??a hablar de cu??ndo es adecuado para redondear valores intermedios, pero de una manera elegante de calcular el determinante utiliza el Bareiss algoritmo, un m??todo exacto por divisi??n basa en Identidad de Sylvester para dar un tiempo de ejecuci??n de orden n 3 y complejidad poco m??s o menos el tama??o de bits de las entradas originales en los tiempos de la matriz n.
Historia
Hist??ricamente, los factores determinantes fueron considerados antes de matrices. Originalmente, un determinante se define como una propiedad de un sistema de ecuaciones lineales . El determinante "determina" si el sistema tiene una soluci??n ??nica (que se produce precisamente si el determinante es distinto de cero). En este sentido, los factores determinantes se utilizaron por primera vez en el libro de texto de matem??ticas BC chino del siglo tercero Los nueve cap??tulos en el arte matem??tico. En Europa, de dos en dos factores determinantes fueron considerados por Cardano al final del siglo 16 y los m??s grandes por Leibniz y, en Jap??n, por Seki cerca de 100 a??os m??s tarde. Cramer (1750) a??ade a la teor??a, el tratamiento del tema en relaci??n con sistemas de ecuaciones. La ley recurrente fue anunciado por primera vez por B??zout (1764).
Fue Vandermonde (1771) que primero determinantes reconocido como funciones independientes. Laplace (1772) dio el m??todo general de ampliar un factor determinante en t??rminos de su complementaria menores: Vandermonde ya hab??a dado un caso especial. Inmediatamente despu??s, Lagrange (1773) trataron determinantes del segundo y tercer orden. Lagrange fue el primero en aplicar determinantes a las preguntas teor??a de la eliminaci??n; demostr?? muchos casos especiales de identidades generales.
Gauss (1801) hizo el siguiente avance. Como Lagrange, hizo mucho uso de los determinantes en la teor??a de los n??meros . Se introdujo la palabra determinantes (Laplace hab??a usado resultante), aunque no en el presente significaci??n, sino m??s bien como aplicada a la discriminante de una cu??ntico. Gauss tambi??n lleg?? a la noci??n de (inversos) determinantes rec??procos, y estuvo muy cerca del teorema de la multiplicaci??n.
El siguiente factor de importancia es Binet (1811, 1812), que declar?? formalmente el teorema relacionada con el producto de dos matrices de m columnas y n filas, que para el caso especial de m = n reduce con el teorema de la multiplicaci??n. En el mismo d??a ( 30 de noviembre de 1812 ) que Binet present?? su documento a la Academia, Cauchy tambi??n present?? uno sobre el tema. (Ver F??rmula de Cauchy-Binet.) En este us?? la palabra determinante en su sentido actual, resumida y simplificada de lo que entonces se conoc??a sobre el tema, mejor?? la notaci??n, y le dio el teorema de multiplicaci??n con una prueba m??s satisfactoria que Binet. Con ??l comienza la teor??a en su generalidad.
La siguiente figura importante era Jacobi (desde 1827). ??l temprana utiliz?? el determinante funcional que Sylvester m??s tarde llam?? la Jacobiano, y en sus memorias en Crelle para 1841 especialmente trata este tema, as?? como la clase de funciones que Sylvester ha llamado alternantes alterna. Sobre el momento de las ??ltimas memorias de Jacobi, Sylvester (1839) y Cayley comenz?? su trabajo.
El estudio de las formas especiales de los determinantes ha sido el resultado natural de la finalizaci??n de la teor??a general. Determinantes simetr??a axial han sido estudiados por Lebesgue, Hesse, y Silvestre; determinantes persymmetric por Sylvester y Hankel; circulants por Catal??n, Spottiswoode, Glaisher, y Scott; determinantes de sesgo y Pfaffians, en relaci??n con la teor??a de la transformaci??n ortogonal, por Cayley; continuants por Sylvester; Wronskians (llamado as?? por Muir) por Christoffel y Frobenius; determinantes compuestos por Sylvester, Reiss, y Picquet; Jacobianos y Arpilleras por Sylvester; y determinantes gauche sim??tricos por Trudi. De los libros de texto sobre el tema Spottiswoode fue la primera. En Estados Unidos, Hanus (1886), Weld (1893), y Muir / Metzler (1933), publicado tratados.