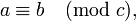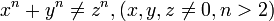Teoría de los números

Temas relacionados: Matemáticas

Antecedentes

Voluntarios SOS ayudaron a elegir artículos e hicieron otro material curricular ¿Quieres saber sobre el patrocinio? Ver www.sponsorachild.org.uk

Teoría de los números es la rama de matemáticas puras se ocupan de las propiedades de los números en general, y los números enteros , en particular, así como las clases más amplias de los problemas que surgen de su estudio.

Teoría de los números se puede subdividir en varios campos, de acuerdo con los métodos utilizados y el tipo de preguntas investigado. (Véase el lista de temas teoría de números.)

El término " aritmética "también se utiliza para referirse a la teoría de números. Este es un término algo más viejo, que ya no es tan popular como lo era antes. Teoría de los números que antes se llamaba la aritmética superior, pero esto también está cayendo en desuso. Sin embargo, todavía aparece en los nombres de los campos matemáticos ( funciones aritméticas, aritmética de curvas elípticas, teorema fundamental de la aritmética ). Este sentido de la expresión aritmética no debe confundirse ni con la aritmética elemental , o con la rama de la lógica de que los estudios Aritmética de Peano como sistema formal. Los matemáticos que trabajan en el campo de la teoría de números se llama teoría de números.

Cuando la organización de los números naturales en una espiral y haciendo hincapié en los números primos, se observa un patrón totalmente explicado intrigante y no, llamado el Espiral de Ulam.

Campos

Teoría de números Primaria

En teoría elemental de números, números enteros se estudian sin el uso de técnicas de otras disciplinas matemáticas. Las cuestiones de divisibilidad , el uso de la Algoritmo de Euclides para calcular máximo común divisor , factorizaciones enteros en números primos , la investigación de los números perfectos y congruencias pertenecen aquí. Varios descubrimientos importantes de este campo son Pequeño teorema de Fermat, El teorema de Euler, la Teorema chino del resto y de la ley de reciprocidad cuadrática. Las propiedades de multiplicativos funciones tales como la Función de Möbius y Función φ de Euler, secuencias enteras, factoriales , y los números de Fibonacci todo también entran en esta área.

Muchas de las preguntas en la teoría de números pueden expresarse en términos de teoría de números elemental, pero pueden requerir un examen muy profundo y nuevos enfoques fuera del ámbito de la teoría de números elemental para resolver. Los ejemplos incluyen:

La conjetura de Goldbach en relación con la expresión de incluso números como sumas de dos números primos.
La conjetura de catalán (ahora Teorema de Mihăilescu) con respecto a potencias enteras sucesivas.
La conjetura gemelo prima sobre la infinitud de pares de primos.
La Collatz conjetura relativa a una iteración simple.
El último teorema de Fermat (declaró en 1637, pero no demostró hasta 1994) relativa a la imposibilidad de encontrar números enteros distintos de cero x, y, z tales que 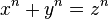$x ^ n + y ^ n = z ^ n$ para algún entero n mayor que 2.

La teoría de la Ecuaciones diofánticas incluso se ha demostrado que es indecidible (ver Décimo problema de Hilbert).

Teoría analítica de números

Teoría analítica de números emplea la maquinaria de cálculo y análisis complejo para hacer frente a preguntas sobre los enteros. La número primo teorema (PNT) y la relacionada Hipótesis de Riemann son ejemplos. El problema de Waring (que representa un entero dado como una suma de plazas, cubos, etc.), la Conjetura de los números primos gemelos (encontrar un número infinito de pares de primera con diferencia 2) y la conjetura de Goldbach (escribiendo incluso enteros como sumas de dos números primos) están siendo atacados con métodos analíticos también. Las pruebas de la trascendencia de constantes matemáticas, tales como π o e, también se clasifican como la teoría de números analítica. Mientras que las declaraciones sobre números trascendentes puede parecer que ha sido eliminada del estudio de los números enteros, que realmente estudian los posibles valores de polinomios con coeficientes enteros evaluados en, por ejemplo, el correo; también están estrechamente relacionados con el campo de la Aproximación Diophantine, donde se investiga "lo bien" un número real dado puede ser aproximado por una racional uno.

Teoría de números algebraicos

En teoría algebraica de números, el concepto de un número se amplió a la números algebraicos que son raíces de polinomios con racionales coeficientes. Estos dominios contienen elementos análogos a los enteros, la denominada solución de enteros algebraicos. En este entorno, las características familiares de los números enteros (por ejemplo, la factorización única) no tienen por qué tienen. La virtud de la maquinaria employed- teoría de Galois , cohomología grupo, la teoría de campos de clase, representaciones de grupo y L-funciones-es que permite recuperar ese orden en parte por esta nueva clase de números.

Muchos números planteamientos teóricos son mejor atacados por estudiarlos módulo p para todos los números primos p (ver campos finitos). Esto se denomina la localización y conduce a la construcción de la números p-adic; este campo de estudio se llama análisis local y surge de la teoría algebraica de números.

Teoría de números geométrica

Teoría de números geométrica (tradicionalmente llamado geometría de los números) incorpora algunos conceptos geométricos básicos, como celosías, a preguntas de teoría de números. Empieza con El teorema de Minkowski sobre puntos de la red en convexa fija, y conduce a las pruebas básicas de la finitud de la número de clase y Unidad teorema de Dirichlet, dos teoremas fundamentales de la teoría algebraica de números.

Teoría de números Combinatoria

Ofertas de teoría de números combinatorios con la teoría de números problemas que implican combinatorias ideas en sus formulaciones o soluciones. Paul Erdös es el principal fundador de esta rama de la teoría de números. Los temas típicos incluyen sistema de recubrimiento, problemas de suma cero, varios sumsets restringidos, y progresiones aritméticas en un conjunto de números enteros. Métodos algebraicos o analíticas son poderosos en este campo.

Teoría de números Computacional

Teoría de números Computacional estudia algoritmos relevantes en la teoría de números. Algoritmos rápidos para pruebas de primera y factorización de enteros tiene importantes aplicaciones en criptografía .

Historia

Teoría de números védica

Los matemáticos en la India estaban interesados en la búsqueda de soluciones integrales de Ecuaciones diofánticas desde el Época védica. El uso geométrica primera de las ecuaciones diofánticas se remonta a la Sulba Sutras, que fueron escritas entre los siglos sexto y octavo antes de Cristo. Baudhayana (c. 800 aC) encontró dos conjuntos de soluciones integrales positivos a un conjunto de ecuaciones diofánticas simultáneas, y también se utiliza ecuaciones diofánticas simultáneas con hasta cuatro incógnitas. Apastamba (c. 600 aC) utiliza ecuaciones diofánticas simultáneas con hasta cinco incógnitas.

Jaina teoría de números

En India, Jaina matemáticos desarrollaron la teoría sistemática más temprana de los números desde el siglo cuarto antes de Cristo hasta el siglo segundo de la CE. (C. 400 aC) El texto Jaina Surya Prajinapti clasifica todos los números en tres conjuntos: enumerables, innumerables e infinitas. Cada uno de éstos se subdividió en tres órdenes:

Enumerable: bajo, intermedio y alto.
Innumerable: casi innumerables, verdaderamente innumerables e innumerable innumerables.
Infinito: casi infinita, verdaderamente infinita, infinitamente infinito.

Los jainistas fueron los primeros en descartar la idea de que todos los infinitos eran el mismo o equivalente. Reconocieron cinco tipos diferentes de infinito: infinitas en una y dos direcciones (una dimensión), infinito en el área (dos dimensiones), infinito en todas partes (tres dimensiones), e infinito perpetuamente (número infinito de dimensiones).

El mayor número N enumerable de los jainistas se corresponde con el concepto moderno de aleph-null 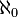$\ Aleph_0$ (El número cardinal del conjunto infinito de números enteros 1, 2, ...), el cardenal más pequeño número transfinito. El jainistas también definió todo un sistema de números cardinales transfinitos, de los cuales 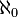$\ Aleph_0$ es el más pequeño.

En la obra Jaina en la teoría de conjuntos , dos tipos básicos de los números transfinitos se distinguen. Por tanto física como razones ontológicas, se hizo una distinción entre asmkhyata y ananata, entre infinitos rígidamente delimitadas y sin apretar acotadas.

Teoría de números griego

Teoría de los números fue un estudio de los favoritos entre los Matemáticos griegos de la época helenística tardía (siglo tercero dC) en Alejandría , Egipto , que eran conscientes de la Concepto ecuación Diophantine en numerosos casos especiales. El primer matemático griego para estudiar estas ecuaciones fue Diofanto.

Diofanto también buscó un método para encontrar soluciones enteras a lineal ecuaciones indeterminadas, ecuaciones que carecen de información suficiente para producir un único conjunto discreto de respuestas. La ecuación 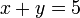$x + y = 5$ es una ecuación. Diofanto descubrió que muchas ecuaciones indeterminadas pueden reducirse a un formulario en una determinada categoría de respuestas se conoce, aunque una respuesta concreta no lo es.

La teoría clásica de numeración indio

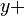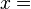Ecuaciones diofánticas fueron estudiados ampliamente por los matemáticos en la India medieval, que fueron los primeros en investigar sistemáticamente métodos para la determinación de soluciones integrales de ecuaciones diofánticas. Aryabhata (499) dio la primera descripción explícita de la solución integral general de la ecuación lineal Diophantine un $y +$ b $x =$ c, que se produce en su texto Aryabhatiya. Este algoritmo kuttaka es considerado como uno de los aportes más significativos de Aryabhata en matemática pura, que encuentran soluciones a las ecuaciones diofánticas mediante fracciones continuas. La técnica fue aplicada por Aryabhata para dar soluciones integrales de ecuaciones diofánticas lineales simulataneous, un problema con importantes aplicaciones en astronomía. También encontró la solución general de la indeterminado ecuación lineal utilizando este método.

Brahmagupta en 628 maneja ecuaciones diofánticas más difíciles. Utilizó el método chakravala resolver cuadráticas ecuaciones diofánticas, incluyendo formas de La ecuación de Pell, tales como 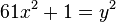$61x ^ 2 + 1 = y ^ 2$ . Su Brahma Sphuta Siddhanta fue traducido al árabe en 773 y fue traducido al latín en 1126. La ecuación 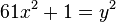$61x ^ 2 + 1 = y ^ 2$ más tarde fue planteado como un problema en 1657 por el francés matemático Pierre de Fermat . La solución general a esta forma particular de la ecuación de Pell fue encontrado más de 70 años más tarde por Leonhard Euler , mientras que la solución general de la ecuación de Pell fue encontrado más de 100 años después por Joseph Louis Lagrange en Hace 1767. Mientras tanto, muchos siglos, la solución general de la ecuación de Pell fue grabado por Bhaskara II en 1150, utilizando una versión modificada del método chakravala de Brahmagupta, que también se utiliza para determinar la solución general a otras ecuaciones cuadráticas indeterminadas y ecuaciones diofánticas cuadráticas. Método chakravala de Bhaskara para encontrar la solución general de la ecuación de Pell era mucho más simple que el método utilizado por Lagrange más de 600 años después. Bhaskara también encontró soluciones a otra cuadrática indeterminada, cúbico, cuarto grado, y de orden superior polinomios ecuaciones. Narayana Pandit mejorar aún más en el método chakravala y encontró soluciones más generales a otra cuadrática indeterminada y de orden superior ecuaciones polinómicas.

Teoría de números islámica

A partir del siglo noveno, Matemáticas islámicas tenían un gran interés en la teoría de números. El primero de estos fue matemáticos Thabit Ibn Qurra, que descubrió un algoritmo que permite pares de números amigos que se encuentran, es decir dos números tales que cada uno es la suma de los divisores apropiados de la otra. En el siglo 10, Al-Baghdadi miró con una ligera variante del método de Thabit Ibn Qurra.

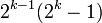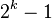En el siglo 10, al-Haitham parece haber sido el primero en tratar de clasificar a todos incluso los números perfectos (números iguales a la suma de sus divisores propios) como los de la forma $2 ^ {k-1} (2 ^ k - 1)$ donde $2 ^ k - 1$ es primo. Al-Haytham es también la primera persona a declarar El teorema de Wilson, a saber, que si p es primo, entonces 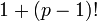$1+ (p-1)!$ es divisible por 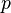$p$ . No está claro si él sabía cómo demostrar este resultado. Se llama el teorema de Wilson debido a un comentario hecho por Edward Waring en 1770 que John Wilson había notado el resultado. No hay evidencia de que John Wilson sabía cómo probarlo y ciertamente Waring no lo hizo. Lagrange dio la primera prueba en 1771.

Números amigos jugaron un papel importante en las matemáticas islámicas. En el siglo 13, Matemático persa Al-Farsi dio una nueva demostración del teorema de Thabit Ibn Qurra, la introducción de nuevas e importantes ideas sobre la factorización y métodos combinatorios. También le dio el par de números amigables 17.296, 18.416 que se han atribuido a Euler, pero sabemos que estos eran conocidos antes que al-Farsi, quizás incluso por el propio Thabit Ibn Qurra. En el siglo 17, Muhammad Baqir Yazdi dio el par de números amigos 9.363.584 y 9.437.056 todavía muchos años antes de que la contribución de Euler.

Teoría de números Europeo Temprano

Teoría de los números se inició en Europa en los siglos 16 y 17, con François Viète, Bachet de Meziriac, y especialmente Fermat , cuyo método de descenso infinito era la primera prueba general de preguntas diofánticas. el último teorema de Fermat se planteó como un problema en 1637, una prueba de que no se ha encontrado hasta 1994. Fermat también planteó la ecuación 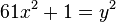$61x ^ 2 + 1 = y ^ 2$ como un problema en 1657.

En el siglo XVIII, Euler y Lagrange hicieron importantes contribuciones a la teoría de números. Euler hizo algunos trabajos en teoría analítica de números, y se encontró una solución general de la ecuación 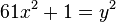$61x ^ 2 + 1 = y ^ 2$ . Lagrange encontró una solución a la ecuación más general de Pell. Euler y Lagrange resolver estas ecuaciones por medio de Pell fracciones continuas, aunque esto era más difícil que la de la India método chakravala.

Los comienzos de la teoría de números moderna

A comienzos de los libros del siglo XIX de Legendre (1798), y Gauss juntos las primeras teorías sistemáticas en Europa. Gauss Disquisitiones Arithmeticae (1801), puede decirse para comenzar la moderna teoría de números.

La formulación de la teoría de la congruencias comienza con Disquisitiones de Gauss. Él introdujo el simbolismo

$un \ equiv b \ pmod c,$

y exploró la mayor parte del campo. Chebyshev publicado en 1847 una obra en ruso sobre el tema, y en Francia Serret lo popularizó.

Además de resumir el trabajo previo, Legendre declaró el ley de reciprocidad cuadrática. Esta ley, descubierta por inducción y enunciada por Euler, fue probado por primera vez por Legendre en su Théorie des Nombres (1798) para los casos especiales. Independientemente de Euler y Legendre, Gauss descubrió la ley sobre 1795, y fue el primero en dar una prueba general. La siguiente también han contribuido al tema: Cauchy; Dirichlet cuyo Vorlesungen über Zahlentheorie es un clásico; Jacobi, quien introdujo el Símbolo de Jacobi; Liouville, Zeller (?), Eisenstein, Kummer, y Kronecker. La teoría se extiende para incluir cúbico y reciprocidad de cuarto grado, (Gauss, Jacobi quien primero demostró la ley de la reciprocidad cúbica, y Kummer).

Para Gauss se debe también la representación de números binarios formas cuadráticas.

Teoría de números Primer

Un tema recurrente y productiva en la teoría de números es el estudio de la distribución de los números primos. Carl Friedrich Gauss conjeturó el límite de la cantidad de números primos que no superen un número determinado (el teorema del número primo) cuando era un adolescente.

Chebyshev (1850) dio límites útiles para el número de primos entre dos límites dados. Riemann introducido análisis complejo en la teoría de la Función zeta de Riemann. Esto condujo a una relación entre los ceros de la función zeta y la distribución de los números primos, llevando eventualmente a una prueba de teorema del número primo independiente por Hadamard y de la Vallée Poussin en 1896. Sin embargo, una prueba elemental fue dada más tarde por Paul Erdös y Atle Selberg en 1949. Aquí medios elementales que no utiliza técnicas de análisis complejo; Sin embargo, la prueba está siendo muy ingenioso y difícil. La Hipótesis de Riemann, que le daría una información mucho más precisa, es todavía una cuestión abierta.

Desarrollos del siglo XIX

Cauchy, Poinsot (1845), Lebesgue (1859, 1868), y en particular Hermite han añadido a la materia. En la teoría de las formas ternarias, Eisenstein ha sido un líder, ya él ya HJS Smith se debe también un avance notable en la teoría de las formas en general. Smith dio una clasificación completa de las formas cuadráticas ternarias, y amplió las investigaciones de Gauss referentes reales formas cuadráticas a formas complejas. Las investigaciones sobre la representación de los números por la suma de 4, 5, 6, 7, 8 plazas fueron avanzados por Eisenstein y la teoría fue completada por Smith.

Dirichlet fue el primero en dar una conferencia sobre el tema en una universidad alemana. Entre sus contribuciones es la extensión del último teorema de Fermat :

$x ^ n + y ^ n \ neq z ^ n, (x, y, z \ neq 0, n> 2)$

que Euler y Legendre habían probado para 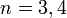$n = 3, 4$ (Y, por tanto, por implicación, todos los múltiplos de 3 y 4), que muestra que Dirichlet 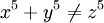$x ^ 5 + y ^ 5 \ neq z ^ 5$ . Entre los escritores franceses posteriores son Borel; Poincaré, cuyas memorias son numerosos y valiosos; Curtiembre, y Stieltjes. Entre los principales contribuyentes en Alemania eran Kronecker, Kummer, Schering, Bachmann, y Dedekind. En Austria Vorlesungen Arithmetik de Stolz allgemeine über (1885-1886), y en Inglaterra Teoría Mathews 'de los Números (Parte I, 1892) eran trabajos académicos generales. Genocchi, Sylvester, y JWL Glaisher también se han sumado a la teoría.

Acontecimientos de finales del siglo XX siglo XIX y principios

Era la época de los grandes avances en la teoría de números, debido a los trabajos de Axel Thue en ecuaciones diofánticas, de David Hilbert en teoría algebraica de números (que también demostró la Del número conjetura primer Waring), y para la creación de teoría de números geométrica por Hermann Minkowski, pero también gracias a Adolf Hurwitz, Georgy F. Voronoy, Waclaw Sierpinski, Derrick Norman Lehmer y varios otros.

Acontecimientos del siglo XX

Las principales figuras en la teoría de números del siglo XX incluyen Hermann Weyl, Nikolai Chebotaryov, Emil Artin, Erich Hecke, Helmut Hasse, Alexander Gelfond, Yuri Linnik, Paul Erdös, Gerd Faltings, GH Hardy, Edmund Landau, Louis Mordell, John Edensor Littlewood, Srinivasa Ramanujan, André Weil, Ivan Vinogradov, Atle Selberg, Carl Ludwig Siegel, Igor Shafarevich, John Tate, Robert Langlands, Goro Shimura, Kenkichi Iwasawa, Jean-Pierre Serre, Pierre Deligne, Enrico Bombieri, Alan Baker, Peter Swinnerton-Dyer, Bryan Birch, Vladimir Drinfeld, Laurent Lafforgue, Andrew Wiles, y Richard Taylor.

Hitos en la teoría de números del siglo XX incluyen la prueba del último teorema de Fermat por Andrew Wiles en 1994 y la prueba de la relacionada Taniyama-Shimura en 1999.

Citas

La matemática es la reina de las ciencias y la teoría de números es la reina de las matemáticas -. Gauss
Dios inventó los números enteros; todo lo demás es obra del hombre. - Kronecker

Recuperado de " http://en.wikipedia.org/w/index.php?title=Number_theory&oldid=195773958 "