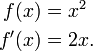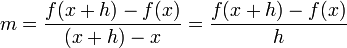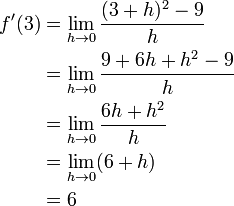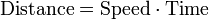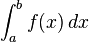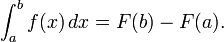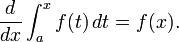C??lculo

C??lculo ( Am??rica , c??lculo, una peque??a piedra utilizada para el recuento) es una rama de las matem??ticas que incluye el estudio de l??mites , derivadas , integrales , y series infinitas, y constituye una parte importante de la educaci??n universitaria moderna. Hist??ricamente, se refiere a veces como "el c??lculo", pero que el uso no es habitual hoy en d??a. C??lculo tiene amplias aplicaciones en la ciencia y la ingenier??a , y se utiliza para resolver problemas complicados para que el ??lgebra es insuficiente. C??lculo se basa en el ??lgebra , la trigonometr??a y la geometr??a anal??tica e incluye dos ramas principales, c??lculo diferencial y c??lculo integral , que est??n relacionados por el teorema fundamental del c??lculo . En matem??ticas m??s avanzadas, c??lculo se suele denominar an??lisis y se define como el estudio de las funciones .

M??s en general, el c??lculo puede referirse a cualquier m??todo o sistema de c??lculo.

Historia

Aryabhatta junto con otros matem??ticos indios durante siglos hechas importante contribuci??n al campo de c??lculo.

Sir Isaac Newton es uno de los m??s famosos contribuyentes al desarrollo del c??lculo, con, entre otras cosas, el uso del c??lculo en sus leyes del movimiento y la gravitaci??n.

Desarrollo

La historia del c??lculo se divide en varios per??odos de tiempo distintos, sobre todo la antigua , medieval , y per??odos modernos. El per??odo antiguo introdujo algunas de las ideas del c??lculo integral, pero no parece haber desarrollado estas ideas en una forma rigurosa y sistem??tica. C??lculo de vol??menes y ??reas, la funci??n b??sica del c??lculo integral, se remonta a la Egipcio Mosc?? papiro (c. 1800 aC), en la que un egipcio calcul?? correctamente el volumen de una pir??mide tronco. Desde la escuela de Matem??ticas griegas, Eudoxo (c. 408-355 aC) utiliz?? el m??todo de agotamiento, que prefigura el concepto del l??mite, para calcular ??reas y vol??menes, mientras que Arqu??medes (c. 287-212 aC) desarroll?? esta idea, inventando heur??stica que se asemejan c??lculo integral . La m??todo de agotamiento fue utilizado m??s adelante en China Liu Hui en el 3er siglo DC con el fin de encontrar el ??rea de un c??rculo. Tambi??n fue utilizado por Zu Chongzhi en el siglo 5 dC, que lo utiliz?? para encontrar el volumen de una esfera .

En el a??o 499 el indio matem??tico Aryabhata usa la noci??n de infinitesimales y expresaron un problema astron??mico en la forma de una base ecuaci??n diferencial . Esta ecuaci??n finalmente llev?? Bhaskara II en el siglo 12 para desarrollar un temprano derivado que representa el cambio infinitesimal, y describi?? una forma temprana de " El teorema de Rolle ". Alrededor de 1000, el AD Matem??tico isl??mico Ibn al-Haytham (Alhazen) fue el primero en obtener la f??rmula para la suma del cuarto poderes , y el uso de inducci??n matem??tica, desarroll?? un m??todo que es f??cilmente generalizable a encontrar la f??rmula para la suma de las integrales poderes, lo cual fue fundamental para el desarrollo del c??lculo integral. En el siglo 12, la Persa matem??tico Sharaf al-Din al-Tusi descubri?? el derivado de polinomios c??bicos, un resultado importante en el c??lculo diferencial. En el siglo 14, Madhava de Sangamagrama, junto con otros matem??tico-astr??nomos de la Escuela de Kerala, describi?? casos especiales de la serie de Taylor , que se tratan en el texto Yuktibhasa.

En la ??poca moderna, se estaban haciendo descubrimientos independientes de c??lculo a principios de siglo 17 Jap??n, por los matem??ticos tales como Seki Kowa, que ampli?? el m??todo de agotamiento. En Europa, la segunda mitad del siglo 17 fue una ??poca de gran innovaci??n. C??lculo proporciona una nueva oportunidad en la f??sica matem??tica para resolver problemas de larga data. Varios matem??ticos han contribuido a estos avances, en particular John Wallis y Isaac Barrow. James Gregory prob?? un caso especial del segundo teorema fundamental del c??lculo en el a??o 1668.

Gottfried Wilhelm Leibniz fue acusado originalmente de plagio de obras in??ditas de Sir Isaac Newton, pero ahora se mira como un inventor independiente y colaborador hacia el c??lculo.

Leibniz y Newton sacaron estas ideas en un todo coherente y por lo general se les atribuye la invenci??n independiente y casi simult??nea de c??lculo. Newton fue el primero en aplicar el c??lculo a general de la f??sica y Leibniz desarroll?? gran parte de la notaci??n utilizada en el c??lculo de hoy; a menudo pasaba d??as determinaci??n s??mbolos apropiados para los conceptos. La idea b??sica que tanto Newton y Leibniz ten??an era el teorema fundamental del c??lculo .

Cuando Newton y Leibniz public?? por primera vez sus resultados, hab??a gran controversia sobre cu??l matem??tico (y, por tanto, en qu?? pa??s) merecido cr??dito. Newton deriv?? sus resultados primero, pero Leibniz public?? por primera vez. Newton afirm?? Leibniz rob?? las ideas de sus notas in??ditas, que Newton hab??a compartido con algunos miembros de la Royal Society. Esta controversia divide matem??ticos de los matem??ticos continentales de habla Ingl??s desde hace muchos a??os, en detrimento de las matem??ticas en ingl??s. Un examen cuidadoso de los papeles de Leibniz y Newton muestra que llegaron a sus resultados de forma independiente, con Leibniz comenzando primero con la integraci??n y Newton con la diferenciaci??n. Hoy en d??a, tanto Newton y Leibniz se le da cr??dito por el desarrollo del c??lculo independiente. Es Leibniz, sin embargo, que dio a la nueva disciplina de su nombre. Newton llam?? a su c??lculo " la ciencia de fluxiones ".

Desde la ??poca de Leibniz y Newton, muchos matem??ticos han contribuido al continuo desarrollo del c??lculo. En el siglo 19, el c??lculo se puso en pie mucho m??s riguroso por los matem??ticos como Cauchy, Riemann , y Weierstrass. Fue tambi??n durante este per??odo que las ideas de c??lculo fueron generalizadas para el espacio euclidiano y el plano complejo . Lebesgue generaliza a??n m??s la noci??n de la integral.

El c??lculo es un tema omnipresente en la mayor??a de las escuelas secundarias y universidades modernas, y los matem??ticos de todo el mundo que siga contribuyendo a su desarrollo.

Significado

Mientras que algunas de las ideas del c??lculo se desarrollaron antes, en Grecia, China, India , Irak, Persia, y Jap??n, el uso moderno de c??lculo se inici?? en Europa , durante el siglo 17, cuando Isaac Newton y Gottfried Wilhelm Leibniz construyeron sobre el trabajo de los matem??ticos anteriores para introducir los principios b??sicos de c??lculo. Este trabajo tuvo un fuerte impacto en el desarrollo de la f??sica .

Aplicaciones del c??lculo diferencial incluyen operaciones en que intervienen la velocidad y la aceleraci??n , los pendiente de una curva, y optimizaci??n. Aplicaciones del c??lculo integral incluyen operaciones en que intervienen ??rea , volumen , longitud del arco, centro de masa , trabajo , y presi??n. Aplicaciones m??s avanzadas incluyen series de potencias y Las series de Fourier. C??lculo se puede utilizar para calcular la trayectoria de un acoplamiento de transporte en una estaci??n espacial o la cantidad de nieve en un camino de entrada.

C??lculo Tambi??n se utiliza para obtener una comprensi??n m??s precisa de la naturaleza del espacio, tiempo y movimiento. Durante siglos, los matem??ticos y fil??sofos lucharon con paradojas que implica divisi??n por cero o sumas de infinitos n??meros. Estas preguntas surgen en el estudio del movimiento y la zona . El griego antiguo fil??sofo Zen??n dio varios ejemplos famosos de tales paradojas. C??lculo proporciona herramientas, especialmente el l??mite y la serie infinita, que resuelve las paradojas.

Cimientos

En matem??ticas, las fundaciones se refiere a la desarrollo riguroso de un sujeto a partir de axiomas y definiciones precisas. La elaboraci??n de una base rigurosa para c??lculos matem??ticos ocup?? durante gran parte del siglo siguiente Newton y Leibniz, y sigue siendo, en cierta medida un ??rea activa de investigaci??n hoy en d??a.

Hay m??s de un enfoque riguroso a la fundaci??n de c??lculo. El habitual es a trav??s del concepto de l??mites definidos en el continuo de n??meros reales . Una alternativa es an??lisis no est??ndar, en la que el sistema de n??meros reales se aumenta con infinitesimal y n??meros infinitos. Las bases de c??lculo se incluyen en el ??mbito de an??lisis real, que contiene definiciones completas y pruebas de los teoremas del c??lculo, as?? como las generalizaciones como medir la teor??a y la teor??a de la distribuci??n.

Principios

L??mites y Infinitesimales

C??lculo generalmente se desarrolla mediante la manipulaci??n de cantidades muy peque??as. Hist??ricamente, el primer m??todo de hacerlo era por infinitesimales. Estos son los objetos que pueden ser tratadas como n??meros, pero que son, en cierto sentido, "infinitamente peque??o". En una recta num??rica, ??stos ser??an lugares que no son cero, pero que tienen distancia cero de cero. No hay un n??mero distinto de cero es un infinitesimal, porque su distancia de cero es positivo. Cualquier m??ltiplo de un infinitesimal sigue siendo infinitamente peque??o, en otras palabras, los infinitesimales no satisfacen la Axioma de Arqu??medes. Desde este punto de vista, el c??lculo es una colecci??n de t??cnicas para manipular los infinitesimales. Este punto de vista cay?? en desgracia en el siglo 19, ya que es dif??cil tomar la noci??n de una precisi??n infinitesimal. Sin embargo, el concepto fue revivido en el siglo 20 con la introducci??n de an??lisis no est??ndar, que proporciona una base s??lida para la manipulaci??n de los infinitesimales.

En el siglo 19, los infinitesimales fueron reemplazados por l??mites . L??mites describen el valor de una funci??n en un cierto aporte en t??rminos de sus valores de la entrada cerca. Capturan comportamiento a peque??a escala, al igual que los infinitesimales, pero utilizando n??meros ordinarios. Desde este punto de vista, el c??lculo es una colecci??n de t??cnicas para la manipulaci??n de ciertos l??mites. Infinitesimales reemplazados por n??meros muy peque??os, y lo infinitamente peque??o comportamiento de la funci??n se encuentra tomando el comportamiento l??mite para los n??meros cada vez m??s peque??os. Los l??mites son f??ciles de poner fundamentos rigurosos, y por esta raz??n son el m??todo est??ndar para el c??lculo.

Derivados

L??nea tangente en (x, f (x)). La derivada f '(x) de una curva en un punto es la pendiente (aumento de m??s de correr) de la l??nea tangente a la curva en ese punto.

El c??lculo diferencial es el estudio de la definici??n, propiedades y aplicaciones de la derivada o pendiente de una gr??fica. El proceso de encontrar la derivada se llama diferenciaci??n. En lenguaje t??cnico, el derivado es una operador lineal, que introduce una funci??n y emite una segunda funci??n, de modo que en cada punto el valor de la salida es la pendiente de la entrada.

El concepto de la derivada es fundamentalmente m??s avanzado que los conceptos encontrados en ??lgebra. En ??lgebra, los estudiantes aprenden acerca de las funciones que introducir un n??mero y la salida de otro n??mero. Por ejemplo, si las entradas de la funci??n de duplicaci??n 3, a continuaci??n, se da salida a 6, mientras que si las entradas de la funci??n de elevaci??n al cuadrado 3, emite 9. Pero las entradas derivados de una funci??n y salidas de otra funci??n. Por ejemplo, si las entradas de derivados de la funci??n de elevaci??n al cuadrado, entonces se env??a la funci??n de duplicaci??n, porque la funci??n de duplicaci??n da la pendiente de la funci??n de la cuadratura en cualquier punto dado.

Para entender la derivada, los estudiantes deben aprender la notaci??n matem??tica. En notaci??n matem??tica, un s??mbolo com??n para la derivada de una funci??n es una marca-ap??strofe como llamada prime. As??, la derivada de f es f '(hablado "f prima"). La ??ltima frase del p??rrafo anterior, en notaci??n matem??tica, se escribir??a

Si la entrada de una funci??n es el tiempo, entonces la derivada de esa funci??n es la velocidad a la que la funci??n cambia.

Si una funci??n es lineal (es decir, si el gr??fica de la funci??n es una l??nea recta), entonces la funci??n se puede escribir y = mx + b, donde:

.

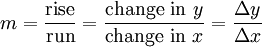Esto da un valor exacto para la pendiente de una l??nea recta. Si la funci??n no es una l??nea recta, sin embargo, entonces el cambio en y dividido por el cambio en x var??a, y se puede utilizar el c??lculo para encontrar un valor exacto en un punto dado. (Tenga en cuenta que y y f (x) representan lo mismo:. La salida de la funci??n) una l??nea a trav??s de dos puntos en una curva se llama una l??nea secante. La pendiente, o aumento de m??s de correr, de una l??nea secante se pueden expresar como

donde el coordenadas del primer punto son (x, f (x)) y h es la distancia horizontal entre los dos puntos.

Para determinar la pendiente de la curva, se utiliza el l??mite de:

.

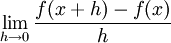La elaboraci??n de un caso particular, nos encontramos con la pendiente de la funci??n de elevaci??n al cuadrado en el punto donde la entrada es 3 y la salida es 9 (es decir, f (x) = x ^2, por lo que f (3) = 9).

La pendiente de la funci??n de elevaci??n al cuadrado en el punto (3, 9) es 6, es decir, que va hasta seis veces m??s r??pido que va a la derecha.

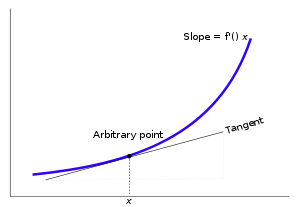
El proceso de l??mite se acaba de describir se puede generalizar a cualquier punto de la gr??fica de cualquier funci??n. El procedimiento se puede visualizar como en la siguiente figura.

Tangente como l??mite de las l??neas secantes. La derivada f '(x) de una curva en un punto es la pendiente de la l??nea tangente a la curva en ese punto. Esta pendiente se determina considerando el valor l??mite de las pendientes de rectas secantes.

Aqu?? la funci??n de que se trate (dibujado en rojo) es f (x) = x ³ - x. La l??nea tangente (en verde) que pasa por el punto (-3/2, -15/8) tiene una pendiente de 23/4. Tenga en cuenta que las escalas verticales y horizontales en esta imagen son diferentes.

Integrales

C??lculo integral es el estudio de las definiciones, propiedades y aplicaciones de los dos conceptos relacionados, la integral indefinida y la integral definida. El proceso de encontrar el valor de una integral se denomina integraci??n. En lenguaje t??cnico, c??lculo integral estudia dos relacionados operadores lineales.

La integral indefinida es la primitiva, la operaci??n inversa a la derivada. F es una integral indefinida de f, donde f es un derivado de F. (Este uso de letras may??sculas y min??sculas para una funci??n y su integral indefinida es com??n en los c??lculos.)

Las entradas integral definida una funci??n y da salida a un n??mero, que da el ??rea entre la gr??fica de la entrada y el eje x . La definici??n t??cnica de la integral definida es el l??mite de una suma de ??reas de rect??ngulos, llamado Suma de Riemann.

Un ejemplo es motivar a las distancias recorridas en un tiempo dado.

Si la velocidad es constante, s??lo se necesita la multiplicaci??n, pero si los cambios de velocidad, entonces necesitamos una m??s potente m??todo para encontrar la distancia. Uno de tales m??todos es la aproximaci??n de la distancia recorrida por romper el tiempo en muchos intervalos cortos de tiempo, a continuaci??n, multiplicando el tiempo transcurrido en cada intervalo por una de las velocidades en ese intervalo, y despu??s tomando la suma (a Riemann suma) de la distancia aproximada recorrida en cada intervalo. La idea b??sica es que si s??lo un corto tiempo transcurrido, entonces la velocidad se mantendr?? m??s o menos lo mismo. Sin embargo, una suma de Riemann s??lo da una aproximaci??n de la distancia recorrida. Debemos tomar el l??mite de todas las sumas de Riemann para encontrar la distancia exacta recorrida.

La integraci??n puede ser pensado como midiendo el ??rea bajo una curva, definida por f (x), entre dos puntos (aqu?? A y B).

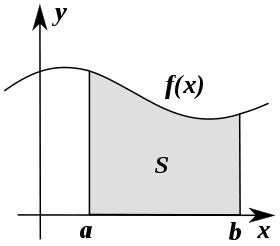
Si f (x) en el diagrama de la izquierda representa la velocidad, ya que var??a con el tiempo, la distancia recorrida entre los tiempos representados por A y B es el ??rea de la regi??n sombreada s.

Para aproximar esa ??rea, un m??todo intuitivo ser??a dividir la distancia entre A y B en un n??mero de segmentos iguales, la longitud de cada segmento representado por el s??mbolo? X. Para cada segmento peque??o, podemos optar por un valor de la funci??n f (x). Llame a ese valor h. Entonces el ??rea del rect??ngulo con la base y la altura h Dx da la distancia (tiempo Dx multiplica por la velocidad h) recorrida en ese segmento. Asociado con cada segmento es el valor promedio de la funci??n por encima de ella, f (x) = h. La suma de todos estos rect??ngulos da una aproximaci??n de la zona entre el eje y la curva, que es una aproximaci??n de la distancia total recorrida. Un valor menor para Dx dar?? m??s rect??ngulos y en la mayor??a de los casos una mejor aproximaci??n, pero para una respuesta exacta que necesita tomar un l??mite? X se aproxima a cero.

El s??mbolo de la integraci??n es 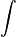, Una S alargada (que significa "suma"). La integral definida se escribe como:

y se lee "la integral de A a B de f -OF- x con respecto a x."

La integral indefinida, o primitiva, est?? escrito:

.

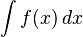Funciones que difieren en s??lo una constante tienen el mismo derivado, y por lo tanto la primitiva de una funci??n dada es en realidad una familia de funciones que difieren s??lo por una constante. Puesto que la derivada de la funci??n y = x ?? + C, donde C es cualquier constante, es y '= 2 x, la primitiva de este ??ltimo viene dada por:

.

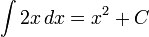Una constante indeterminada como C en el antiderivative se conoce como una constante de integraci??n.

Teorema fundamental

El teorema fundamental del c??lculo indica que la diferenciaci??n y la integraci??n son operaciones inversas. M??s precisamente, se refiere a los valores de primitivas a las integrales definidas. Debido a que por lo general es m??s f??cil de calcular una primitiva de aplicar la definici??n de una integral definida, el teorema fundamental del c??lculo proporciona una forma pr??ctica de calcular integrales definidas. Tambi??n se puede interpretar como una indicaci??n precisa del hecho de que la diferenciaci??n es la inversa de la integraci??n.

El teorema fundamental del c??lculo establece que: Si una funci??n f es continua en el intervalo [a, b], y si F es una funci??n cuya derivada es f en el intervalo (a, b), entonces

Adem??s, para cada x en el intervalo (a, b),

Esta toma de conciencia, hecho tanto por Newton y Leibniz , que basa sus resultados en trabajos anteriores de Isaac Barrow, fue clave para la proliferaci??n masiva de los resultados anal??ticos despu??s de su trabajo lleg?? a ser conocido. El teorema fundamental proporciona un m??todo algebraico de computaci??n muchas integrales-sin realizar l??mite definido procesos mediante la b??squeda de f??rmulas para primitivas. Tambi??n es una soluci??n de prototipo de una ecuaci??n diferencial . Ecuaciones diferenciales relacionan una funci??n desconocida de sus derivados, y son ubicuos en las ciencias.

Aplicaciones

La espiral logar??tmica de la Nautilus Shell es una imagen cl??sica utilizada para representar el crecimiento y el cambio en relaci??n con el c??lculo

El c??lculo se utiliza en todas las ramas de las ciencias f??sicas , de la inform??tica , las estad??sticas , la ingenier??a , la econom??a , los negocios , la medicina , y en otros campos donde un problema puede ser modelado matem??ticamente y una se desea soluci??n ??ptima.

F??sica hace uso particular de c??lculo; todos los conceptos de la mec??nica cl??sica se interrelacionan a trav??s de c??lculo. La masa de un objeto de conocida la densidad , la momento de inercia de los objetos, as?? como la energ??a total de un objeto dentro de un campo conservador puede ser encontrado por el uso del c??lculo. En los subcampos de la electricidad y el magnetismo c??lculo se puede utilizar para encontrar el total flujo de los campos electromagn??ticos. Un ejemplo m??s hist??rica de la utilizaci??n de c??lculo en la f??sica es la segunda ley de Newton del movimiento , utiliza expresamente el t??rmino "velocidad de cambio" que se refiere a la derivada: La velocidad de cambio de impulso de un cuerpo es igual a la fuerza que act??a resultante en el cuerpo y est?? en la misma direcci??n. Incluso la expresi??n com??n de la segunda ley de Newton como Fuerza = masa ?? aceleraci??n implica el c??lculo diferencial debido a la aceleraci??n se puede expresar como la derivada de la velocidad. Teor??a de Maxwell del electromagnetismo y de Einstein teor??a de la relatividad general tambi??n se expresa en el lenguaje del c??lculo diferencial.

C??lculo se puede utilizar en conjunci??n con otras disciplinas matem??ticas. Por ejemplo, se puede utilizar con ??lgebra lineal para encontrar el "mejor ajuste" aproximaci??n lineal para un conjunto de puntos en un dominio.

En el ??mbito de la medicina, el c??lculo se puede utilizar para encontrar el ??ngulo ??ptimo de ramificaci??n de un vaso sangu??neo con el fin de maximizar el flujo.

En la geometr??a anal??tica , el estudio de gr??ficas de funciones, c??lculo se utiliza para encontrar puntos altos y puntos bajos (m??ximos y m??nimos), pendiente, concavidad y puntos de inflexi??n.

En econom??a, c??lculo permite la determinaci??n de la ganancia m??xima, proporcionando una manera de calcular f??cilmente tanto el costo marginal y el ingreso marginal.

C??lculo se puede utilizar para encontrar soluciones aproximadas a las ecuaciones, en m??todos tales como el m??todo de Newton , iteraci??n de punto fijo, y aproximaci??n lineal. Por ejemplo, la nave espacial utilizar una variaci??n de la M??todo de Euler para aproximar cursos curvas dentro de los entornos de gravedad cero.