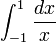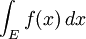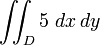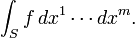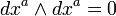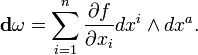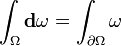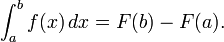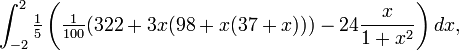Integral
Antecedentes de las escuelas de Wikipedia
Esta selecci??n wikipedia ha sido elegido por los voluntarios que ayudan Infantil SOS de Wikipedia para esta Selecci??n Wikipedia para las escuelas. Una buena manera de ayudar a otros ni??os es mediante el patrocinio de un ni??o
- La palabra "integral" (adjetivo) tambi??n puede significar: "ser un n??mero entero ".
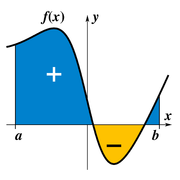
La integraci??n es un concepto b??sico de avanzadas matem??ticas , espec??ficamente en los campos de c??lculo y an??lisis matem??tico . Dada una funci??n f (x) de un verdadero x variable y un intervalo [a, b] de la recta real, la integral
es igual a la zona de una regi??n en el plano xy xy limitada por el gr??fica de f, el eje x, y la vertical l??neas x = a y x = b, con ??reas por debajo del eje x va a restar.
El t??rmino "integral" tambi??n puede referirse a la noci??n de antiderivative, una funci??n F cuya derivada es la funci??n f dada. En este caso se llama una integral indefinida, mientras que las integrales discutidos en este art??culo se denominan integrales definidas. Algunos autores sostienen una distinci??n entre primitivas e integrales indefinidas.
Los principios de integraci??n fueron formuladas por Isaac Newton y Gottfried Leibniz en el siglo XVII. A trav??s del teorema fundamental del c??lculo , que se desarrollaron de forma independiente, la integraci??n est?? conectado con diferenciaci??n, y la integral definida de una funci??n se pueden calcular f??cilmente una vez que se conoce una primitiva. Integrales y derivadas se convirtieron en las herramientas b??sicas de c??lculo , con numerosas aplicaciones en la ciencia y la ingenier??a.
Una definici??n matem??tica rigurosa de la integral se dio por Bernhard Riemann . Se basa en una limitaci??n de procedimiento que se aproxima al ??rea de una regi??n curvil??nea rompiendo la regi??n en losas verticales delgadas. A partir del siglo XIX, las nociones m??s sofisticadas de integral comenzaron a aparecer, donde el tipo de la funci??n, as?? como el dominio sobre el cual se realiza la integraci??n se ha generalizado. La integral de l??nea se define para las funciones de dos o tres variables, y el intervalo de integraci??n [a, b] se sustituye por una cierta curva que conecta dos puntos en el plano o en el espacio. En un integral de superficie, la curva se sustituye por una pieza de una superficie en el espacio tridimensional. Integrales de formas diferenciales desempe??an un papel fundamental en la moderna geometr??a diferencial . Estas generalizaciones de integrante primero surgieron de las necesidades de la f??sica , y juegan un papel importante en la formulaci??n de muchas leyes f??sicas, en particular las de electrodin??mica. Los conceptos modernos de la integraci??n se basan en la teor??a matem??tica abstracta conocida como la integraci??n de Lebesgue , desarrollado por Henri Lebesgue.
Historia
Integraci??n Pre-c??lculo
La integraci??n puede rastrearse ya en el antiguo Egipto, alrededor del a??o 1800 antes de Cristo, con la Papiro de Mosc?? demostrar el conocimiento de una f??rmula para el volumen de un piramidal tronco. La t??cnica sistem??tica primero documentado capaz de integrales determinantes es la m??todo de agotamiento de los Eudoxo (circa 370 aC), que pretend??a encontrar ??reas y vol??menes, rompiendo para arriba en un n??mero infinito de formas para el que era conocido el ??rea o volumen. Este m??todo fue desarrollado y empleado por Arqu??medes y se utiliza para calcular las ??reas de par??bolas y una aproximaci??n a la ??rea de un c??rculo. M??todos similares se desarrollaron de forma independiente en China alrededor del siglo 3 dC por Liu Hui, que lo utiliz?? para encontrar el ??rea del c??rculo. Este m??todo fue utilizado m??s adelante por Zu Chongzhi para encontrar el volumen de una esfera. Algunas ideas del c??lculo integral se encuentran en el Siddhanta Shiromani, un texto 12?? astronom??a siglo por el matem??tico indio Bhaskara II.
Avances significativos en t??cnicas como el m??todo de agotamiento no comenzaron a aparecer hasta el siglo 16o. En este momento el trabajo de Cavalieri con su m??todo de indivisibles, y el trabajo de Fermat , comenz?? a sentar las bases de c??lculo moderno. Otras medidas se hicieron a principios del siglo 17 por Barrow y Torricelli, que proporcion?? los primeros indicios de una conexi??n entre la integraci??n y diferenciaci??n.
Newton y Leibniz
El mayor avance en la integraci??n se produjo en el siglo 17 con el descubrimiento independiente del teorema fundamental del c??lculo por Newton y Leibniz . El teorema demuestra una conexi??n entre la integraci??n y la diferenciaci??n. Esta conexi??n, junto con la relativa facilidad de la diferenciaci??n, puede ser explotado para calcular las integrales. En particular, el teorema fundamental del c??lculo le permite a uno para resolver una clase mucho m??s amplio de problemas. Igual en importancia es el marco matem??tico integral que tanto Newton y Leibniz desarrollaron. Dado el nombre de c??lculo infinitesimal, que permiti?? el an??lisis preciso de las funciones dentro de los dominios continuos. Este marco de tiempo se convirti?? moderno C??lculo , cuya notaci??n para las integrales se extrae directamente de la obra de Leibniz.
La formalizaci??n de las integrales
Mientras que Newton y Leibniz siempre un enfoque sistem??tico para la integraci??n, su trabajo carec??a de un grado de rigor. Obispo Berkeley memorablemente atacado infinitesimales como "los fantasmas de la cantidad difuntos". C??lculo adquiri?? una base m??s firme con el desarrollo de l??mites y se le dio una base adecuada por Cauchy en la primera mitad del siglo 19. La integraci??n fue primero rigurosamente formalizada, utilizando los l??mites, por Riemann . Aunque todos los trozos acotada funciones continuas son Riemann integrable en un intervalo acotado, posteriormente se consideraron funciones m??s generales, a las que no se aplica la definici??n de Riemann, y Lebesgue formulado una definici??n diferente de integral, fundada en medir teor??a. Otras definiciones de integral, ampliando los enfoques de Riemann y Lebesgue de, se propusieron.
Notaci??n
Isaac Newton utiliz?? una peque??a barra vertical sobre una variable para indicar la integraci??n, o se coloca la variable dentro de una caja. La barra vertical se confunde f??cilmente con 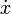 o
o 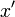 , Que Newton utiliza para indicar la diferenciaci??n y la notaci??n caja era dif??cil para impresoras para reproducir, por lo que estas anotaciones no fueron ampliamente adoptado.
, Que Newton utiliza para indicar la diferenciaci??n y la notaci??n caja era dif??cil para impresoras para reproducir, por lo que estas anotaciones no fueron ampliamente adoptado.
La notaci??n moderna para la integral indefinida fue introducido por Gottfried Leibniz en 1675 (Burton 1988, p 359;. Leibniz 1899, p 154.). Adapt?? el s??mbolo integral "∫", desde una letra S alargada, de pie para summa (del lat??n, "suma" o "total"). La notaci??n moderna para la integral definida, con los l??mites superior e inferior del signo integral, se utiliz?? por primera vez por Joseph Fourier en M??moires de la Academia Francesa en torno a 1819-1820, reimpreso en su libro de 1822 (Cajori 1929, pp 249-250;. Fourier 1822, ??231). En Notaci??n matem??tica ??rabe que se escribe de derecha a izquierda, un s??mbolo integral invertida 22px se utiliza (W3C 2006).
Terminolog??a y notaci??n
Si una funci??n tiene una integral, se dice que es integrable. La funci??n para la que se calcula la integral se llama el integrando. La regi??n sobre la cual se est?? integrando una funci??n se llama el dominio de la integraci??n. Si la integral no tiene un dominio de integraci??n, se considera indefinido (uno con un dominio se considera definitivo). En general, el integrando puede ser una funci??n de m??s de una variable, y el dominio de la integraci??n puede ser un ??rea, volumen, una regi??n dimensional superior, o incluso un espacio abstracto que no tiene una estructura geom??trica en ning??n sentido usual.
El caso m??s simple, la integral de una funci??n real f de una variable real x en el intervalo [a, b], se denota por
El signo ∫, una "S" alargada, representa la integraci??n; a y b son el l??mite inferior y l??mite superior de integraci??n, que define el ??mbito de la integraci??n; f es el integrando, para ser evaluados como x var??a en el intervalo [a, b ]; y dx puede tener diferentes interpretaciones en funci??n de la teor??a que se utiliza. Por ejemplo, se puede ver simplemente como una notaci??n que indica que x es la "variable ficticia" de la integraci??n, como un reflejo de los pesos de la suma de Riemann, una medida (en la integraci??n de Lebesgue y sus extensiones), un infinitesimal (no en -Est??ndar an??lisis) o como una cantidad matem??tica independiente: una forma diferencial. Los casos m??s complicados pueden variar ligeramente la notaci??n.
Introducci??n
Integrales aparecen en muchas situaciones pr??cticas. Considere la posibilidad de una piscina. Si es rectangular, a continuaci??n, a partir de su longitud, anchura, y profundidad podemos determinar f??cilmente el volumen de agua que puede contener (a llenarlo), el ??rea de su superficie (para cubrirlo), y la longitud de su borde (a cuerda de ??l). Pero si es ovalada, con un fondo redondeado, todas estas cantidades llaman para integrales. Aproximaciones pr??cticas pueden ser suficientes al principio, pero al final nos exigir respuestas exactas y rigurosas a este tipo de problemas.

Para empezar, tenga en cuenta la curva y = f (x) entre x = 0 yx = 1, con f (x) = √ x. Le pedimos:
- ??Cu??l es el ??rea bajo la funci??n f en el intervalo de 0 a 1?
y llamar a esta ??rea (todav??a desconocido) la integral de f. La notaci??n para esta integral ser??
Como primera aproximaci??n, mira la unidad cuadrada dada por los lados x = 0 hasta x = 1 ey = f (0) = 0 ey = f (1) = 1. Su superficie es exactamente 1. Tal como es, el verdadero valor de la integral debe ser algo menor. Disminuir el ancho de los rect??ngulos de aproximaci??n dar?? un mejor resultado; por lo que cruzar el intervalo en cinco pasos, utilizando los puntos de aproximaci??n 0, 1/5, 2/5, y as?? sucesivamente a 1. Montar una caja para cada etapa utilizando la altura del extremo derecho de cada pieza curva, por lo tanto √ 1/5, √ 2/5, y as?? sucesivamente hasta √1 = 1. Sumando las ??reas de estos rect??ngulos, obtenemos una mejor aproximaci??n para la integral buscada, es decir,
N??tese que estamos tomando una suma de un n??mero finito de valores de la funci??n de f, multiplicados por las diferencias de dos puntos de aproximaci??n posteriores. Podemos ver f??cilmente que la aproximaci??n es todav??a demasiado grande. El uso de m??s pasos produce una aproximaci??n m??s cercana, pero nunca ser?? exacta: la sustituci??n de los 5 subintervalos por doce como se representa, nos pondremos un valor aproximado para la zona de 0.6203, que es demasiado peque??o. La idea clave es la transici??n de la adici??n de un n??mero finito de las diferencias de puntos de aproximaci??n multiplicados por sus respectivos valores de la funci??n a usar infinitamente fina, o pasos infinitesimales.
En cuanto al c??lculo real de integrales, el teorema fundamental del c??lculo , debido a Newton y Leibniz, es el v??nculo fundamental entre las operaciones de la diferenciaci??n y la integraci??n. Aplicado a la curva de la ra??z cuadrada, f (x) = x 1/2, lo dice a mirar a la funci??n relacionada F (x) = 2/3 x 3/2, y simplemente tomar F (1) - F (0) , donde 0 y 1 son los l??mites de la intervalo [0,1]. (Este es un caso de una regla general, que para f (x) = x q, con q ≠ -1, la funci??n relacionada, el llamado antiderivative es F (x) = (x 1 q) / (q + 1)). As?? que el valor exacto del ??rea bajo la curva se calcula formalmente como
La notaci??n
concibe la integral como una suma ponderada, denotado por la "S" alargada, con valores de la funci??n, f (x), multiplicado por anchuras de paso infinitesimales, los llamados diferenciales, denotado por dx. El signo de multiplicaci??n se omite generalmente.
Hist??ricamente, tras el fracaso de los esfuerzos iniciales para interpretar rigurosamente infinitesimales, Riemann integrales define formalmente como un l??mite de sumas ponderadas, para que el dx sugiri?? el l??mite de una diferencia (es decir, el ancho del intervalo). Las deficiencias de la dependencia de Riemann en intervalos y continuidad motivado nuevas definiciones, especialmente la integral de Lebesgue , que se basa en la capacidad de extender la idea de la "medida" de manera mucho m??s flexible. Por lo tanto la notaci??n
se refiere a una suma ponderada en la que se dividen los valores de la funci??n, con μ medir el peso a asignar a cada valor. Aqu?? A indica la regi??n de integraci??n.
Geometr??a diferencial , con su "c??lculo de colectores ", da la notaci??n familiar pero otra interpretaci??n. Ahora f (x) dx y convertirse en una forma diferencial, ω = f (x) dx, un nuevo operador diferencial d, conocido como el aparece derivada exterior, y el teorema fundamental se convierte en el m??s general El teorema de Stokes,
de los cuales Teorema de Green, el teorema de la divergencia, y el teorema fundamental del c??lculo seguimiento.
M??s recientemente, los infinitesimales han reaparecido con rigor, a trav??s de innovaciones modernas como an??lisis no est??ndar. No s??lo estos m??todos reivindican las intuiciones de los pioneros, que tambi??n conducen a nuevas matem??ticas.
Aunque hay diferencias entre estas concepciones de la integral, hay una considerable superposici??n. As??, el ??rea de la superficie de la piscina ovalada puede ser manejado como una elipse geom??trico, como una suma de los infinitesimales, como una integral de Riemann, como una integral de Lebesgue, o como un colector con una forma diferencial. El resultado calculado ser?? la misma para todos.
Las definiciones formales
Hay muchas maneras de definir formalmente una integral, no todos los cuales son equivalentes. Las diferencias existen sobre todo para hacer frente a diferentes casos especiales que pueden no ser integrable bajo otras definiciones, sino tambi??n de vez en cuando por razones pedag??gicas. Las definiciones m??s utilizadas de integral son integrales de Riemann e integrales de Lebesgue.
Integral de Riemann

La integral de Riemann se define en t??rminos de Riemann sumas de funciones con respecto a las particiones etiquetadas de un intervalo. Deje [a, b] ser un intervalo cerrado de la l??nea real; entonces una partici??n de etiquetado de [a, b] es una secuencia finita

Esto divide el intervalo [a, b] en i subintervalos [x i -1, x i], cada uno de los cuales est?? "marcado" con un punto t distinguido i ∈ [x i -1, x i]. Deje Δ i = x i - x i -1 ser?? la anchura de subintervalo i; a continuaci??n, la malla de una partici??n tales etiquetado es la anchura de la m??s grande sub-intervalo formado por la partici??n, max i = 1 ... n Δ i. Una suma de Riemann de una funci??n f con respecto a una partici??n tales etiquetados se define como
por lo tanto cada t??rmino de la suma es el ??rea de un rect??ngulo con la altura igual al valor de la funci??n en el punto distinguida de la sub-intervalo dado, y una anchura igual a la anchura de subintervalo. La integral de Riemann de una funci??n f en el intervalo [a, b] es igual a S si:
- Por todo ε> 0 existe δ> 0 tal que, para cualquier partici??n etiquetada [a, b] con malla inferior a δ, tenemos
Cuando las etiquetas elegidas dan la m??xima (respectivamente, m??nima) valor de cada intervalo, la suma de Riemann se convierte en una parte superior (respectivamente, inferior) Suma Darboux, lo que sugiere la estrecha relaci??n entre la integral de Riemann y la Darboux integral.
Integral de Lebesgue
La integral de Riemann no est?? definido para una amplia gama de funciones y situaciones de importancia en las aplicaciones (y de inter??s en la teor??a). Por ejemplo, la integral de Riemann puede integrar f??cilmente la densidad de encontrar la masa de una viga de acero, pero no puede dar cabida a una bola de acero que descansa sobre ella. Esto motiva a otras definiciones, en las que un surtido m??s amplio de funciones es integrable (Rudin, 1987). La integral de Lebesgue, en particular, logra una gran flexibilidad al dirigir la atenci??n a los pesos en la suma ponderada.
La definici??n de la integral de Lebesgue por lo tanto comienza con una medida, μ. En el caso m??s simple, el Medida de Lebesgue μ (A) de un intervalo de A = [a, b] es su anchura, b - a, de modo que la integral de Lebesgue est?? de acuerdo con la (propia) integral de Riemann cuando ambos existen. En casos m??s complicados, los conjuntos est??n medidos pueden estar muy fragmentadas, sin continuidad y no se parece a intervalos.
Para aprovechar esta flexibilidad, las integrales de Lebesgue revertir el enfoque de la suma ponderada. Como Folland (1984, p. 56) dice, "Para calcular la integral de Riemann de f, se divide el dominio [a, b] en subintervalos", mientras que en la integral de Lebesgue, "uno es en efecto dividir el rango de f ".
Un enfoque com??n define primero la integral de la funci??n de indicador de un conjunto medible A trav??s de:
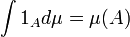 .
.
Esto se extiende por la linealidad de un medible s sencilla funci??n, que alcanza s??lo un n??mero finito, n, de los valores no negativos distintas:
(Donde la imagen de A i bajo la simple funci??n s es el valor de la constante a i). As??, si E es un conjunto medible uno define
Entonces para cualquier no negativo funci??n medible f se define
es decir, la integral de f se ajusta para que sea el supremum de todas las integrales de funciones simples que son menos que o igual a f. Una funci??n f medible en general, se divide en sus valores positivos y negativos mediante la definici??n
Finalmente, f es integrable Lebesgue si
y entonces la integral se define por
Cuando el espacio de medida en la que se definen las funciones es tambi??n una localmente compacto espacio topol??gico (como es el caso con los n??meros reales R), las medidas compatibles con la topolog??a en un sentido adecuado ( Medidas de Radon, de los cuales la medida de Lebesgue es un ejemplo) y integral con respecto a ellos se puede definir de manera diferente, a partir de las integrales de funciones continuas con soporte compacto. M??s precisamente, las funciones de soporte compacto forman un espacio vectorial que lleva un naturales topolog??a, y (rad??n) medida se pueden definir como cualquier continuo funcional lineal en este espacio; el valor de una medida en una funci??n de soporte compacto es entonces tambi??n, por definici??n, la integral de la funci??n. Uno procede entonces para expandir la medida (la integral) a las funciones m??s generales por la continuidad, y define la medida de un conjunto como la integral de la funci??n de indicador. Este es el enfoque adoptado por Bourbaki (2004) y un cierto n??mero de otros autores. Para m??s detalles ver Medidas de Radon.
Otros integrales
Aunque las integrales de Riemann y Lebesgue son las definiciones m??s importantes de la integral, un n??mero de otros existe, incluyendo:
- La Integral de Riemann-Stieltjes, una extensi??n de la integral de Riemann.
- La Lebesgue-Stieltjes integral, desarrollada posteriormente por Johann Radon, que generaliza el Riemann-Stieltjes y Lebesgue integrales .
- La Daniell integral, que subsume la integral de Lebesgue y Lebesgue-Stieltjes integral sin la dependencia de medidas.
- La Henstock-Kurzweil integral, definido de diversas maneras por Arnaud Denjoy, Oskar Perron, y (lo m??s elegante, como el indicador integral) Jaroslav Kurzweil, y desarrollado por Ralph Henstock.
Propiedades de la integraci??n
Linealidad
- La colecci??n de funciones integrables Riemann en un intervalo cerrado [a, b] forma un espacio vectorial bajo las operaciones de adici??n puntual y la multiplicaci??n por un escalar, y la operaci??n de la integraci??n
- es un funcional lineal en este espacio vectorial. Por lo tanto, en primer lugar, la colecci??n de funciones integrables es cerrado bajo la asunci??n combinaciones lineales; y, en segundo lugar, la integral de una combinaci??n lineal es la combinaci??n lineal de las integrales,
- Del mismo modo, el conjunto de bienes -valued funciones integrables Lebesgue en un dado medir el espacio de E con μ medida es cerrado bajo tomar combinaciones lineales y por lo tanto forman un espacio vectorial, y la integral de Lebesgue
- es un funcional lineal en este espacio vectorial, de manera que
- De manera m??s general, considere el espacio vectorial de todas funciones medibles en un espacio de medida (E μ,), que toman valores en un localmente compacto completo topol??gica espacio vectorial V sobre un localmente compacto K campo topol??gico, f: E → V. Entonces uno puede definir un mapa de la integraci??n abstracta asignando a cada funci??n f un elemento de V o el s??mbolo ∞,
- que es compatible con las combinaciones lineales. En esta situaci??n, la linealidad se mantiene para el subespacio de funciones cuya integral es un elemento de V (es decir, "finito"). Los m??s importantes casos especiales surgen cuando K es R, C, o una extensi??n finita del campo Q p de n??meros p-adic, y V es un espacio vectorial de dimensi??n finita sobre K, y cuando K = C y V es un complejo Espacio de Hilbert.
Linealidad, junto con algunas propiedades de continuidad naturales y normalizaci??n para una cierta clase de funciones "simples", se puede utilizar para dar una definici??n alternativa de la integral. Este es el enfoque de Daniell para el caso de funciones reales en un conjunto X, generalizada por Nicolas Bourbaki a las funciones con valores en un espacio localmente compacto vectorial topol??gico. Ver (Hildebrandt 1953) para una caracterizaci??n axiom??tica de la integral.
Las desigualdades de las integrales
Una serie de desigualdades generales sostenga para Riemann integrables funciones definidas en un cerrado y delimitada intervalo [a, b] y se puede generalizar a otras nociones de integral (Lebesgue y Daniell).
- Los l??mites superiores e inferiores. Una funci??n f integrable en [a, b], es necesariamente delimitada en ese intervalo. As??, hay n??meros reales my M para que m ≤ f (x) ≤ M para todo x de [a, b]. Dado que las sumas inferior y superior de f sobre [a, b] son por lo tanto limitado por, respectivamente, m (b - a) y M (b - a), se deduce que
- Las desigualdades entre funciones. Si f (x) ≤ g (x) para cada x en [a, b], entonces cada una de las sumas superior e inferior de f est?? acotada por encima de las sumas superior e inferior, respectivamente, de g. As??
- Esta es una generalizaci??n de las desigualdades anteriores, como M (b - a) es la integral de la funci??n constante con el valor M sobre [a, b].
- Subintervalos. Si [c, d] es un subintervalo de [a, b] yf (x) es no negativa para todo x, entonces
- Productos y valores absolutos de funciones. Si fyg son dos funciones, entonces podemos considerar su productos pointwise y poderes, y valores absolutos :
- Si f es Riemann integrable en [a, b], entonces el mismo es cierto para | f |, y
- Por otra parte, si fyg son ambas Riemann-integrable, f 2, g 2, y fg son tambi??n Riemann integrable, y
- Esta desigualdad, conocido como el Desigualdad de Cauchy-Schwarz, juega un papel destacado en Hilbert teor??a del espacio, donde el lado izquierdo se interpreta como la producto interno de dos funciones cuadrado-integrables F y G en el intervalo [a, b].
- La desigualdad de H??lder. Supongamos que p y q son dos n??meros reales, 1 ≤ p, q ≤ ∞ con 1 / p + 1 / q = 1, y f y g son dos funciones Riemann integrables. Entonces la funci??n | f | p y | g | q tambi??n son integrables y la siguiente La desigualdad de H??lder sostiene:
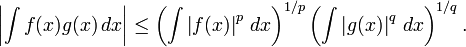
- Para p = q = 2, la desigualdad de H??lder se convierte en la desigualdad de Cauchy-Schwarz.
- La desigualdad de Minkowski. Supongamos que p ≥ 1 es un n??mero real y f y g son funciones Riemann integrables. Entonces | f | p, | g | p y | f + g | p son tambi??n Riemann integrable y la siguiente Minkowski desigualdad se cumple:
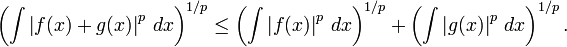
- Un an??logo de esta desigualdad de Lebesgue integral se utiliza en la construcci??n de L espacios p.
Convenciones
En esta secci??n f es una de valor real Riemann integrable funci??n . La integral
en un intervalo [a, b] se define si a <b. Esto significa que las sumas superior e inferior de la funci??n f se eval??an en un una partici??n = x 0 ≤ x ≤ 1. . . ≤ x n = b cuyos valores x i van en aumento. Geom??tricamente, esto significa que la integraci??n se lleva a cabo "izquierda a derecha", evaluando f dentro de los intervalos [x i, x i + 1] donde un intervalo con un ??ndice m??s alto se encuentra a la derecha de uno con un ??ndice inferior. Los valores de a y b, los puntos finales de la intervalo, se llaman el l??mites de integraci??n de f. Integrales tambi??n se pueden definir si a> b:
- Revertir l??mites de integraci??n. Si a> b entonces a definir
Esto, con a = b, implica:
- Integrales en intervalos de longitud cero. Si A es un n??mero real entonces
La primera convenci??n es necesaria la consideraci??n de tomar integrales sobre subintervalos de [a, b]; el segundo dice que una integral en un intervalo de degenerado, o una punto, debe ser cero . Una de las razones por primera convenci??n es que la integrabilidad de f en un intervalo [a, b] implica que f es integrable en cualquier subintervalo [c, d], pero en las integrales particulares tienen la propiedad de que:
- Si c es cualquier aditividad de la integraci??n en intervalos. elemento de [a, b], entonces
Con la primera convenci??n de la relaci??n resultante
est?? entonces bien definido para cualquier permutaci??n c??clica de a, b, y c.
En lugar de considerar lo anterior como convenciones, tambi??n se puede adoptar el punto de vista de que la integraci??n se realiza en variedades orientadas solamente. Si M es un colector de m-dimensional tal orientado, y M 'es el mismo bloque con orientaci??n opuesta y ω es una m -forma, entonces uno ha (ver m??s abajo para la integraci??n de formas diferenciales):
Teorema fundamental del c??lculo
El teorema fundamental del c??lculo es la afirmaci??n de que la diferenciaci??n y la integraci??n son operaciones inversas: si un funci??n continua se integra primero y luego diferenciado, se recupera la funci??n original. Una consecuencia importante, a veces llamado el segundo teorema fundamental del c??lculo, le permite a uno computar integrales mediante el uso de un antiderivada de la funci??n a integrar.
Declaraciones de teoremas
- Teorema fundamental del c??lculo. Sea f una de valor real integrable funci??n definida en un intervalo cerrado [a, b]. Si F est?? definida para x en [a, b] por
- entonces F es continua en [a, b]. Si f es continua en x en [a, b], entonces F es diferenciable en x, y F '(x) = f (x).
- Segundo teorema fundamental del c??lculo. Sea f una funci??n integrable con valores reales definida en un intervalo cerrado [a, b]. Si F es una funci??n tal que F '(x) = f (x) para todo x en [a, b] (es decir, F es una primitiva de f), a continuaci??n,
- Corolario. Si f es una funci??n continua en [a, b], entonces f es integrable en [a, b], y F, definido por
- es un anti-derivada de f en [a, b]. Por otra parte,
Extensiones
Integrales impropias
Un "buen" integral de Riemann asume el integrando es definido y finito en un intervalo cerrado y acotado, delimitado por los l??mites de integraci??n. Una integral impropia se produce cuando una o m??s de estas condiciones no se cumple. En algunos casos tales integrales pueden ser definidos por teniendo en cuenta el l??mite de una secuencia de adecuada Riemann integrales en intervalos cada vez m??s grandes.
Si el intervalo es ilimitado, por ejemplo en su extremo superior, entonces la integral impropia es el l??mite en ese punto final tiende a infinito.
Si el integrando s??lo se define o finita en un intervalo semiabierto, por ejemplo (a, b], entonces otra vez un l??mite puede proporcionar un resultado finito.
Es decir, la integral impropia es el l??mite de integrales adecuados como un punto final del intervalo de integraci??n se acerca o bien un determinado n??mero real , o ∞ o -∞. En casos m??s complicados, se requieren l??mites en ambos extremos, o en puntos interiores.
Consideremos, por ejemplo, la funci??n 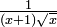 integrado de 0 a ∞ (a la derecha). En el l??mite inferior, cuando x va a 0 la funci??n va a ∞, y el l??mite superior es en s?? ∞, aunque la funci??n va a 0. Por lo tanto se trata de una doble integral impropia. Integrado, por ejemplo, de 1 a 3, una suma ordinaria Riemann es suficiente para producir un resultado de
integrado de 0 a ∞ (a la derecha). En el l??mite inferior, cuando x va a 0 la funci??n va a ∞, y el l??mite superior es en s?? ∞, aunque la funci??n va a 0. Por lo tanto se trata de una doble integral impropia. Integrado, por ejemplo, de 1 a 3, una suma ordinaria Riemann es suficiente para producir un resultado de 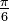 . Integrar de 1 a ∞, una suma de Riemann no es posible. Sin embargo, cualquier l??mite superior finito, dicen t (con t> 1), da un resultado bien definido,
. Integrar de 1 a ∞, una suma de Riemann no es posible. Sin embargo, cualquier l??mite superior finito, dicen t (con t> 1), da un resultado bien definido, 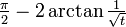 . Esto tiene un l??mite finito cuando t tiende a infinito, es decir,
. Esto tiene un l??mite finito cuando t tiende a infinito, es decir, 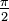 . Del mismo modo, la integral desde 1/3 a 1 permite a una suma de Riemann, as??, casualmente produciendo de nuevo
. Del mismo modo, la integral desde 1/3 a 1 permite a una suma de Riemann, as??, casualmente produciendo de nuevo 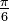 . Sustituci??n de un tercio por un valor positivo arbitrario s (con s <1) es igual de seguro, dando
. Sustituci??n de un tercio por un valor positivo arbitrario s (con s <1) es igual de seguro, dando 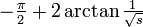 . Esto, tambi??n, tiene un l??mite finito como s tiende a cero, es decir,
. Esto, tambi??n, tiene un l??mite finito como s tiende a cero, es decir, 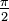 . La combinaci??n de los l??mites de los dos fragmentos, el resultado de esta integral es impropia
. La combinaci??n de los l??mites de los dos fragmentos, el resultado de esta integral es impropia
Este proceso no se garantiza el ??xito; un l??mite puede dejar de existir, o puede ser ilimitada. Por ejemplo, en el intervalo acotado de 0 a 1 la integral de 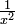 no converge; y en el intervalo de 1 a ∞ sin l??mites la integral de
no converge; y en el intervalo de 1 a ∞ sin l??mites la integral de 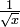 no converge.
no converge.
Tambi??n puede suceder que un integrando es ilimitada en un punto interior, en cuyo caso la integral debe dividirse en ese punto, y debe existir las integrales l??mite en ambos lados y debe ser limitada. As??
Pero la integral parecido
No se puede asignar un valor de esta manera, como las integrales por encima y por debajo de cero no hacerlo de forma independiente converger. (Sin embargo, vea Cauchy valor principal.)
Integración múltiple
Integrales se pueden tomar más de regiones distintas de intervalos. En general, una integral sobre un conjunto E de una función f se escribe:
Aquí x no tiene que ser un número real, pero puede ser otra cantidad adecuada, por ejemplo, un vector en R 3 . teorema de Fubini muestra que tales integrales pueden reescribirse como una integral iterada . En otras palabras, la integral se puede calcular mediante la integración de una coordenada a la vez.
Así como la integral definida de una función positiva de una variable representa eláreade la región entre la gráfica de la función y laxeje x, laintegral doblede una función positiva de dos variables representa elvolumende la región entre la superficie definida por la función y el plano que contiene su dominio.(El mismo volumen puede obtenerse a través de laintegral triple- la integral de una función en tres variables - de la función constantef(x,y,z) = 1 sobre la región antes mencionada entre la superficie y el plano). Si el número de variables es mayor, entonces la integral representa unhipervolumen, un volumen de un sólido de más de tres dimensiones que no pueden ser graficados.
Por ejemplo, el volumen de laparalelepípedo de lados 4 × 6 × 5 puede obtenerse de dos maneras:
- Por la integral doble
- de la funciónf(x,y) = 5 calculado en la regiónDen laxyplano xy que es la base del paralelepípedo.
- Por la integral triple
- de la función constante 1 calculado sobre la propia paralelepípedo.
Debido a que es imposible calcular laantiderivada de una función de más de una variable,indefinidano existen integrales múltiples, por lo que tales integrales son todosdefinitivo.
Integrales de línea
El concepto de una integral puede extenderse a dominios más generales de integración, tales como líneas y superficies curvas. Tales integrales son conocidas como integrales de línea y las integrales de superficie respectivamente. Estos tienen importantes aplicaciones en la física, como cuando se trata de campos de vectores.
Una línea integral (a veces llamado un camino integral ) es una integral donde la función de ser integrado se evalúa a lo largo de una curva . Varios diferentes integrales de línea están en uso. En el caso de una curva cerrada que también se llama una integral de contorno .
La función de ser integrado puede ser un campo escalar o un campo vectorial. El valor de la integral de línea es la suma de los valores del campo en todos los puntos de la curva, ponderado por alguna función escalar en la curva (comúnmente longitud de arco o, para un vector campo, el producto escalar del campo vectorial con un vector diferencial en la curva). Esta ponderación se distingue la línea integral de las integrales simples definidos en intervalos. Muchas fórmulas simples de la física tienen análogos continuos naturales en términos de integrales de línea; por ejemplo, el hecho de que el trabajo es igual a la fuerza multiplicada por la distancia puede expresarse (en términos de cantidades vectoriales) como:
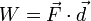 ;
;
que es paralela a la integral de línea:
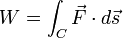 ;
;
que resume componentes del vector a lo largo de una trayectoria continua, y por lo tanto se encuentra el trabajo realizado sobre un objeto que se mueve a través de un campo, tal como un campo eléctrico o gravitacional
Integrales de superficie
Un integral de superficie es una integral definida tomado más de un superficie (que puede ser una curva conjunto en el espacio); que puede ser pensado como el analógico integral doble de la integral de línea. La función de ser integrado puede ser un campo escalar o un campo vectorial. El valor de la integral de superficie es la suma del campo en todos los puntos en la superficie. Esto se puede lograr mediante la división de la superficie en elementos de superficie, que proporcionan el particionamiento para sumas de Riemann.
Para un ejemplo de las aplicaciones de las integrales de superficie, considere un campo vector v sobre una superficie S ; es decir, para cada punto x en S , v ( x ) es un vector. Imaginemos que tenemos un fluido que fluye a través de S , de tal modo que v ( x ) determina la velocidad del fluido en x . La de flujo se define como la cantidad de fluido que fluye a través de S en cantidad unidad de tiempo. Para encontrar el flujo, tenemos que tomar el producto escalar de v con la unidad de superficie normal a S en cada punto, lo que nos dará un campo escalar, que integramos sobre la superficie:
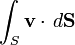 .
.
El flujo de fluido en este ejemplo puede ser de un fluido física tal como agua o aire, o de flujo eléctrico o magnético. Así integrales de superficie tienen aplicaciones en la física , en particular con la teoría clásica de electromagnetismo .
Integrales de formas diferenciales
La forma diferencial es un concepto matemático en los campos decálculo multivariable,topología diferencial y tensores.la notación moderna de la forma diferencial, así como la idea de las formas diferenciales como losproductos de cuña dederivados exteriores que forman unálgebra exterior, fue presentado por ??lie Cartan.
Inicialmente Trabajamos en un conjunto abierto en R n . A 0-forma se define como una función suave f . Cuando integramos una función f sobre un m - dimensional subespacio S de R n , escribimos como
(Los superíndices son índices, no exponentes.) Podemos considerar dx 1 través dx n ser propios objetos formales, en lugar de las etiquetas adjuntas para hacer integrales parecen Riemann resume. Alternativamente, podemos verlos como covectores, y por lo tanto una medida de la "densidad" (de ahí integrable en un sentido general). Llamamos a la dx 1 , ..., dx n básicos 1- formas .
Definimos elproducto exterior, "???", un operador bilineal "multiplicación" de estos elementos, con laalternanciapropiedad que
para todos los índices a . Tenga en cuenta que la alternancia junto con linealidad implica dx b ??? dx la = - dx la ??? dx b . Esto también asegura que el resultado del producto de cuña tiene una orientación.
Definimos el conjunto de todos estos productos para ser básico 2- formas , y del mismo modo se define el conjunto de productos de la forma dx la ??? dx b ??? dx c ser básica 3- formas . Un general k -forma es entonces una suma ponderada de básicos k- formas, donde los pesos son las funciones lisa f . Juntos forman un espacio vectorial con básicos k -formas como los vectores de la base, y 0-formas (funciones suaves) como el campo de escalares. El producto cuña luego se extiende a k -formas de la manera natural. Con el R n en la mayoría de n covectores puede ser linealmente independientes, así una k- formulario con k > n siempre será cero, por la propiedad alterna.
Además del producto de cuña, también existe el exterior derivado operador d . Esto mapas operador k -formas de ( k 1) -formas. Para una k ?? -forma = f dx la sobre R n , definimos la acción de d por:
con extensión a lo generalk-formas que ocurre linealmente.
Este enfoque más general permite un enfoque más natural coordinar libre a la integración de los colectores . También permite una generalización natural del teorema fundamental del cálculo , llamado teorema de Stokes, que podemos afirmar que
donde ?? es un general k -forma, y ????? denota el límite de la región ??. Así, en el caso de que ?? es una forma de 0 y ?? es un intervalo cerrado de la línea real, esto reduce al teorema fundamental del cálculo . En el caso de que ?? es una forma 1 y ?? es una región 2-dimensional en el plano, el teorema se reduce a teorema de Green. Del mismo modo, el uso de 2-formas, y 3-formas y Hodge dualidad, podemos llegar a teorema de Stokes y la teorema de la divergencia. De esta manera podemos ver que las formas diferenciales proporcionan una poderosa visión unificadora de la integración.
Métodos y aplicaciones
Integrales Informática
La técnica más básica para el cálculo de las integrales de una variable real se basa en el teorema fundamental del cálculo . Se procede así:
- Elija una funciónf(x) y un intervalo [a,b].
- Encontrar una primitiva def, es decir, una funciónFtal queF '=f.
- Por el teorema fundamental del cálculo, siempre que el integrando e integral no tienensingularidades en el camino de la integración,
- Por lo tanto el valor de la integral esF(b) -F(un).
Tenga en cuenta que la integral no es en realidad la antiderivada, pero el teorema fundamental nos permite utilizar primitivas para evaluar integrales definidas.
El paso difícil a menudo encontrar una primitiva de f . Rara vez es posible echar un vistazo a una función y anote su antiderivada. Más a menudo, es necesario utilizar una de las muchas técnicas que se han desarrollado para evaluar integrales. La mayoría de estas técnicas reescribir una integral como una diferente que es de esperar más manejable. Las técnicas incluyen:
- Integración por sustitución
- Integración por partes
- Integración por sustitución trigonométrica
- Integración por fracciones parciales
- Integración mediante fórmulas de reducción
Incluso si estas técnicas fallan, todavía puede ser posible evaluar una integral dado. La siguiente técnica más común es el cálculo residuo, mientras que para las integrales no elementales serie de Taylor a veces puede ser usado para encontrar el antiderivative. También hay muchos menos comunes formas de calcular integrales definidas; por ejemplo, identidad de Parseval puede ser utilizado para transformar una integral sobre una región rectangular en una suma infinita. De vez en cuando, una integral puede evaluarse mediante un truco; un ejemplo de esto, vea integral de Gauss.
Los cálculos de volúmenes desólidos de revolución por lo general se puede hacer conla integración de disco ola integración shell.
Los resultados específicos que se han trabajado a cabo mediante diversas técnicas se recogen en lalista de las integrales.
Algoritmos simbólicos
Muchos de los problemas en las matemáticas, la física y la ingeniería implican la integración en donde se desea una fórmula explícita para la integral. Extenso tablas de integrales se han compilado y publicado en los últimos años para este propósito. Con la difusión de las computadoras , muchos profesionales, educadores y estudiantes han recurrido a sistemas de álgebra computacional que están específicamente diseñados para realizar tareas difíciles o tediosas, incluyendo la integración. Integración simbólica presenta un desafío especial en el desarrollo de este tipo de sistemas.
Una dificultad importante en la integración matemática simbólica es que en muchos casos, simplemente no existe una fórmula cerrada para la primitiva de una función más bien inocentemente mirando. Por ejemplo, se sabe que las primitivas de las funciones exp ( x 2 ), x X y el pecado x / x no puede ser expresado en la forma cerrada que implica sólo racionales y exponenciales funciones, logaritmo , trigonométricas y funciones trigonométricas inversas, y las operaciones de multiplicación y la composición; en otras palabras, ninguna de las tres funciones dadas es integrable en funciones elementales. la teoría de Galois diferencial proporciona criterios generales que permiten determinar si la primitiva de una función elemental es elemental. Por desgracia, resulta que las funciones con expresiones cerradas de primitivas son la excepción y no la regla. En consecuencia, los sistemas informatizados de álgebra no tienen esperanza de ser capaz de encontrar una antiderivada de una función elemental construida al azar. En el lado positivo, si los "bloques de construcción" para primitivas están fijados de antemano, puede todavía ser posible decidir si la antiderivada de una función dada puede expresarse usando estos bloques y operaciones de multiplicación y composición, y para encontrar el respuesta simbólica siempre existe. La algoritmo de Risch, implementado en Mathematica y los Arce sistemas de álgebra computacional, hace exactamente eso para las funciones y primitivas construidas a partir de las funciones racionales, radicales, logaritmos y funciones exponenciales.
Algunos integrandos especiales ocurren con suficiente frecuencia como para justificar un estudio especial. En particular, puede ser útil tener, en el conjunto de primitivas, las funciones especiales de la física (como las funciones de Legendre, la función hipergeométrica, la función gamma y así sucesivamente). Extendiendo el algoritmo de Risch-Norman para que incluya estas funciones es posible pero difícil.
La mayoría de los seres humanos no son capaces de integrar estas fórmulas generales, por lo que en cierto sentido los ordenadores son más hábiles en la integración de fórmulas muy complicadas. Muy fórmulas complejas es probable que tengan de forma cerrada primitivas, por lo que la cantidad de una ventaja hace presente es una pregunta filosófica que está abierto para el debate.
Cuadratura numérica
Las integrales se encuentran en un curso básico de cálculo son elegidos deliberadamente por simplicidad; las que se encuentran en aplicaciones reales no son siempre tan complaciente. Algunas integrales no se puede encontrar exactamente, algunos requieren funciones especiales que sí son un reto para calcular, y otros son tan complejos que encontrar la respuesta exacta es demasiado lento. Esto motiva el estudio y aplicación de métodos numéricos para integrales de aproximación, que utilizan hoy flotante aritmética de punto en electrónicos digitales ordenadores . Muchas de las ideas surgió mucho antes, para los cálculos de la mano; pero la velocidad de las computadoras de propósito general como el ENIAC creó la necesidad de mejoras.
Los objetivos de la integración numérica son la precisión, fiabilidad, eficiencia y generalidad. Métodos sofisticados pueden superar ampliamente un método ingenuo por las cuatro medidas (Dahlquist y Björck próximas; Kahaner, Moler & Nash 1989; Stoer y Bulirsch 2002). Consideremos, por ejemplo, la integral
que tiene la respuesta exacta 94 / 25 = 3,76. (En la práctica ordinaria, la respuesta no se conoce de antemano, por lo que una tarea importante - no explorado aquí -. Es decidir cuándo una aproximación es lo suficientemente bueno) Un "libro de cálculo" enfoque divide el rango de integración en, digamos, 16 piezas iguales, y calcula valores de la función.
Valores de la función espaciados x -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 f(x) 2.22800 2.45663 2.67200 2.32475 0.64400 -0.92575 -0.94000 -0.16963 0.83600 x -1.75 -1.25 -0.75 -0.25 0.25 0.75 1.25 1.75 f(x) 2.33041 2.58562 2.62934 1.64019 -0.32444 -1.09159 -0.60387 0.31734
Usando el extremo izquierdo de cada pieza, el método rectángulo resume 16 valores de la función y se multiplica por el ancho de paso, h , 0,25 aquí, para obtener un valor aproximado de 3,94325 para la integral. La precisión no es impresionante, pero el cálculo utiliza formalmente piezas de anchura infinitesimal, por lo que inicialmente puede parecer poco motivo de preocupación. De hecho, doblando varias veces el número de pasos eventualmente produce una aproximación de 3,76001. Sin embargo 2 18 se requieren piezas, un gran costo computacional para tan poca precisión; y un alcance para una mayor precisión puede obligar a pasos tan pequeños que la precisión aritmética se convierte en un obstáculo.
Un mejor enfoque reemplaza las tapas horizontales de los rectángulos con las tapas inclinadas tocar la función en los extremos de cada pieza. Este regla del trapecio es casi tan fácil de calcular; que resume todos los 17 valores de la función, pero los pesos de la primera y la última por un medio, y de nuevo se multiplica por el ancho de paso. Esto mejora inmediatamente la aproximación a 3,76925, que es notablemente más precisa. Además, sólo 2 10 se necesitan piezas de lograr 3,76000, sustancialmente menor que el método de cálculo rectángulo de precisión comparable.
Método de Romberg se basa en el método trapezoidal con gran efecto. En primer lugar, las longitudes de paso se reducen a la mitad de forma incremental, dando aproximaciones trapezoidales denotados por T ( h 0 ), T ( h 1 ), y así sucesivamente, donde h k1 es un medio de h k . Para cada nuevo tamaño de paso, sólo la mitad de los nuevos valores de la función deben ser computados; los otros se transfieren de tamaño anterior (como se muestra en la tabla anterior). Pero la idea es realmente potente para interpolar un polinomio a través de las aproximaciones, y extrapolar a T (0). Con este método, una forma numérica exacta respuesta aquí requiere sólo cuatro piezas (cinco valores de función)! La Lagrange polinomio de interpolación { h k , T ( h k )} k= 0 ... 2 = {(4.00,6.128), (2.00,4.352), (1.00,3.908)} es 3.76 + 0.148 h 2 , produciendo el valor extrapolado 3.76 en h = 0.
Cuadratura de Gauss requiere a menudo notablemente menos trabajo para una precisión superior. En este ejemplo, se puede calcular los valores de la función en sólo dos x posiciones, ± 2 / ???3 , haga doble cada valor y la suma para obtener la respuesta numérica exacta. La explicación de este éxito espectacular se encuentra en análisis de errores, y un poco de suerte. Un n- método de Gauss punto es exacta para polinomios de grado hasta 2 n -1. La función en este ejemplo es un polinomio de grado 3, más un término que cancela porque los puntos finales elegidos son simétricas en torno a cero. (Cancelación también se beneficia el método de Romberg.)
Desplazamiento de la gama dejó un poco, por lo que la integral es -2,25-1,75, elimina la simetría. Sin embargo, el método trapezoidal es bastante lento, el método de interpolación polinómica de Romberg es aceptable, y el método de Gauss requiere la menor trabajo - si el número de puntos se conoce de antemano. Además, la interpolación racional puede utilizar las mismas evaluaciones trapezoidales como el método de Romberg con mayor eficacia.
Cuadratura de comparación de costos método M??todo Trapecio Romberg Racional Gauss Puntos 1048577 257 129 36 Rel.Err. -5,3 × 10-13 -6,3 × 10-15 8,8 × 10-15 3,1 × 10-15 Valor 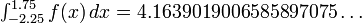
En la práctica, cada método debe utilizar evaluaciones adicionales para asegurar una cota de error de una función desconocida; esto tiende a compensar parte de la ventaja del método de Gauss puro, y motiva al popular híbrido de Gauss-Kronrod. Simetría todavía puede ser explotada mediante el fraccionamiento de esta integral en dos rangos, -2,25 a -1,75 (sin simetría), y -1,75 a 1,75 (simetría). En términos más generales, en cuadratura adaptativa particiones de un rango en pedazos basados ??????en las propiedades de la función, por lo que los puntos de datos se concentran donde más se necesitan.
Esta breve introducción omite integrales de dimensiones superiores (por ejemplo, el área y cálculos de volumen), donde las alternativas tales comola integración Monte Carlo tienen gran importancia.
Un texto de cálculo no es un sustituto para el análisis numérico, pero lo contrario también es cierto. Incluso el mejor código numérico de adaptación a veces requiere un usuario para ayudar con las integrales más exigentes. Por ejemplo, integrales impropias pueden requerir un cambio de variable o métodos que se pueden evitar infinitos valores de la función; y propiedades conocidas como la simetría y periodicidad pueden proporcionar apalancamiento crítico.

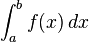
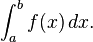
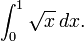
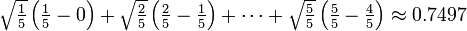
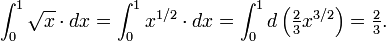
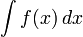
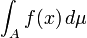
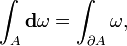
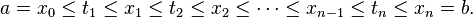
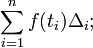
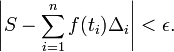
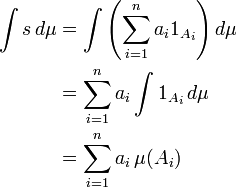
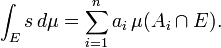
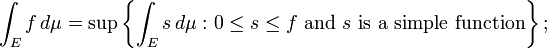

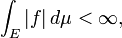
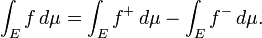
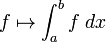
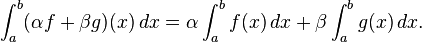
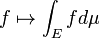
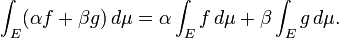
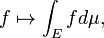
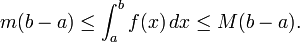
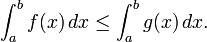
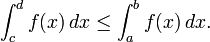
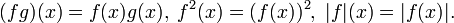
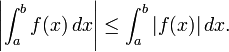
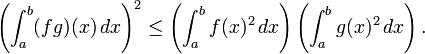
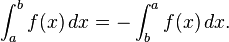
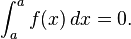
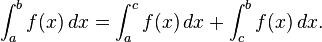
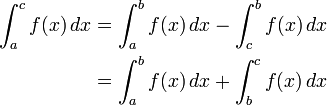
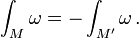
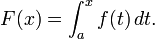
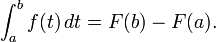
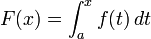

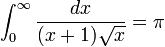
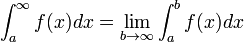
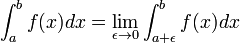
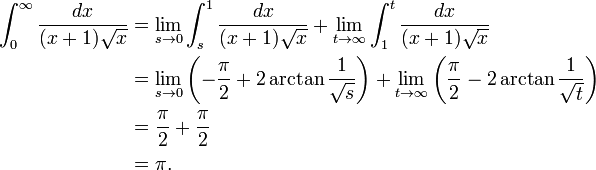
![\ Begin {align} \ int _ {- 1} ^ {1} \ frac {dx} {\ sqrt [3] {x ^ 2}} y {} = \ lim_ {s \ a 0} \ int _ {- 1} ^ {- s} \ frac {dx} {\ sqrt [3] {x ^ 2}} + \ lim_ {t \ a 0} \ int_ {t} ^ {1} \ frac {dx} {\ sqrt [3 ] {x ^ 2}} \\ & {} = \ lim_ {s \ a 0} 3 (1- \ sqrt [3] {s}) + \ lim_ {t \ a 0} 3 (1- \ sqrt [ 3] {t}) \\ & {} = 3 + 3 \\ & {} = 6. \ end {align}](../../images/116/11627.png)