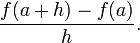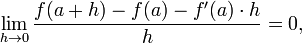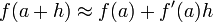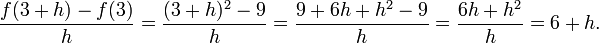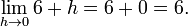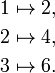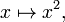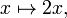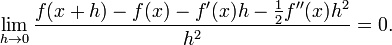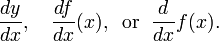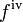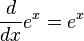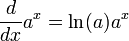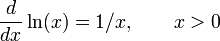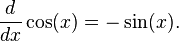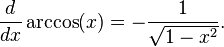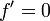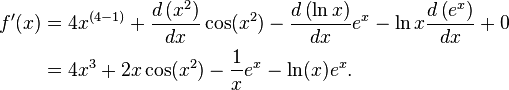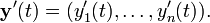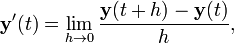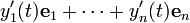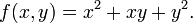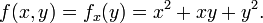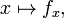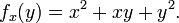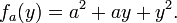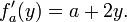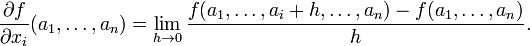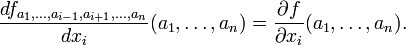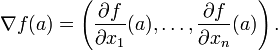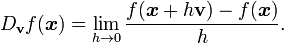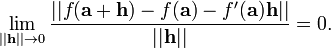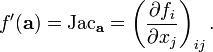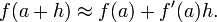Derivado

Temas relacionados: Matem??ticas

Sab??as ...

SOS Children ha intentado que el contenido de Wikipedia m??s accesible por esta selecci??n escuelas. Todos los ni??os disponibles para el apadrinamiento de ni??os de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer m??s ...

La gr??fica de una funci??n, dibujado en negro, y una l??nea tangente a esa funci??n, dibujado en rojo. La pendiente de la l??nea tangente es igual a la derivada de la funci??n en el punto marcado.

En el c??lculo , una rama de las matem??ticas , la derivada es una medida de c??mo una funci??n cambia cuando los valores de sus entradas cambian. En t??rminos generales, un derivado puede ser pensado como la cantidad de una cantidad est?? cambiando en alg??n momento dado. Por ejemplo, la derivada de la posici??n o la distancia de un coche en alg??n momento en el tiempo es la velocidad instant??nea, o velocidad instant??nea (respectivamente), en el que ese coche est?? viajando (a la inversa de la integral de la velocidad es la posici??n del coche).

Una noci??n estrechamente relacionada es la diferencial de una funci??n.

La derivada de una funci??n en un valor de entrada elegido describe la mejor aproximaci??n lineal de la funci??n cerca de ese valor de entrada. Para funci??n con valores reales de una sola variable real, la derivada en un punto es igual a la pendiente de la recta tangente a la gr??fica de la funci??n en ese punto. En dimensiones m??s altas, la derivada de una funci??n en un punto es una transformaci??n lineal llama linealizaci??n ..

El proceso de b??squeda de un derivado se llama diferenciaci??n. El teorema fundamental del c??lculo indica que la diferenciaci??n es el proceso inverso a la integraci??n .

La diferenciaci??n y el derivado de

En cada punto, el derivado es el pendiente de una l??nea que es tangente a la curva . La l??nea roja es siempre tangente a la curva azul; su pendiente es la derivada.

La diferenciaci??n es un m??todo para calcular la velocidad a la que una cantidad, y, los cambios con respecto al cambio en otra cantidad, X, sobre la cual se dependiente. Esta tasa de cambio se llama la derivada de y con respecto a x. En lenguaje m??s preciso, la dependencia de y sobre x significa que y es una funci??n de x. Si x e y son n??meros reales , y si el gr??fica de y se representa frente x, las medidas derivadas de los pendiente de esta gr??fica en cada punto. Esta relaci??n funcional se denota a menudo y = f (x), donde f denota la funci??n.

El caso m??s simple es cuando Y es un funci??n lineal de x, lo que significa que la gr??fica de y contra x es una l??nea recta. En este caso, y = f (x) = m x + c, para los n??meros reales M y C, y la pendiente m est?? dado por

$m = {\ mbox {cambiar en} y \ sobre \ mbox {} en cambiar x} = {\ Delta y \ over {\ Delta x}}$

donde el s??mbolo Δ (la forma may??scula de la letra griega Delta) es una abreviatura de "cambio en el." Esta f??rmula es verdad porque

y + Δ y = f (x + Δ x) = m (x + Δ x) + c = m x + c + m Δ x = y + m Δ x.

De ello se deduce que Δ Δ y = m x.

Esto da un valor exacto para la pendiente de una l??nea recta. Si la funci??n f no es lineal (es decir, su gr??fica no es una l??nea recta), sin embargo, entonces el cambio en y dividido por el cambio en x var??a: la diferenciaci??n es un m??todo para encontrar un valor exacto para esta tasa de cambio en cualquier dado valor de x.

Figura 1. La tangente l??nea en (x, f (x))

Figura 2. La secante a la curva y = f (x) determinado por los puntos (x, f (x)) y (x + h, f (x + h)).

Figura 3. La recta tangente como l??mite de secantes.

La idea, ilustrado por las figuras 1-3, es calcular la tasa de cambio como el valor l??mite de la relaci??n de las diferencias Δ Y / Δ Δ x como x se hace infinitamente peque??o.

En Notaci??n de Leibniz, como un cambio infinitesimal en x se denota por dx, y la derivada de y con respecto a x est?? escrito

$\ Frac {dy} {dx} \, \!$

lo que sugiere la relaci??n de dos cantidades infinitesimales. (La expresi??n anterior se manifiesta en diversas formas, tales como "dy dx por" o "dy sobre dx". La forma "dydx" oral se utiliza a menudo coloquial, aunque puede dar lugar a confusi??n.)

El enfoque m??s com??n para convertir esta idea intuitiva en una definici??n precisa utiliza l??mites , pero hay otros m??todos, tales como an??lisis no est??ndar.

Definici??n a trav??s de cocientes de diferencias

Sea y = f (x) una funci??n de x. En la geometr??a cl??sica, la l??nea tangente en un n??mero real a es la ??nica l??nea por el punto (a, f (a)), que no cumpli?? con la gr??fica de f transversalmente, lo que significa que la l??nea no pasa directamente a trav??s del gr??fico. La derivada de y con respecto a x en A es, geom??tricamente, la pendiente de la recta tangente a la gr??fica de f en a. La pendiente de la l??nea tangente est?? muy cerca de la pendiente de la recta que pasa por (a, f (a)) y un punto cercano en el gr??fico, por ejemplo (a + h, f (a + h)). Estas l??neas se llaman rectas secantes. Un valor de h cercana a cero dar?? una buena aproximaci??n a la pendiente de la recta tangente, y los valores m??s peque??os (en valor absoluto ) de h ser??, en general, dar un mejor aproximaciones. La pendiente de la recta secante es la diferencia entre los valores de y de estos puntos dividido por la diferencia entre los valores de x, es decir,

$\ Frac {f (a + h) -f (a)} {h}.$

Esta expresi??n es Newton 's cociente de diferencias. El derivado es el valor del cociente de diferencias como las l??neas secantes se acercan cada vez m??s cerca de la l??nea tangente. Formalmente, la derivada de la funci??n f en A es el l??mite

$f '(a) = \ lim_ {h \ a 0} {f (a + h) -f (a) \ over h}$

del cociente de diferencias cuando h tiende a cero, si existe este l??mite. Si existe el l??mite, entonces f es diferenciable en a. Aqu?? f '(a) es una de varias notaciones comunes para el derivado ( v??ase m??s adelante ).

De manera equivalente, el derivado satisface la propiedad de que

$\ Lim_ {h \ a 0} {f (a + h) -f (a) - f '(a) \ cdot h \ over h} = 0,$

que tiene la interpretaci??n intuitiva (v??ase la Figura 1) que la l??nea tangente a f en una ofrece la mejor aproximaci??n lineal

$f (a + h) \ aprox f (a) + f '(a) h$

af cerca de una (es decir, por peque??a h). Esta interpretaci??n es la m??s f??cil de generalizar a otros contextos ( v??ase m??s adelante ).

Sustituyendo 0 para h en las causas cociente de diferencias divisi??n por cero, por lo que la pendiente de la l??nea tangente no se pueden encontrar directamente. En lugar de ello, definir Q (h) para ser el cociente de la diferencia como una funci??n de h:

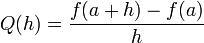$Q (h) = \ frac {f (a + h) - f (a)} {h}$ .

Q (h) es la pendiente de la recta secante entre (a, f (a)) y (a + h, f (a + h)). Si f es una funci??n continua, lo que significa que su gr??fica es una curva continua, sin huecos, entonces Q es una funci??n continua de distancia desde el punto h = 0. Si el l??mite 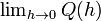$\ Estilo de texto \ lim_ {h \ a 0} Q (h)$ existe, lo que significa que hay una manera de elegir un valor para Q (0) que hace que el gr??fico de Q una funci??n continua, entonces la funci??n f es diferenciable en el punto A, y su derivada en un Q es igual a (0).

En la pr??ctica, la continuidad de la Q cociente de diferencias (h) a h = 0 se muestra mediante la modificaci??n del numerador para cancelar h en el denominador. Este proceso puede ser largo y tedioso para funciones complicadas, y muchos cortes cortos se utilizan com??nmente para simplificar el proceso.

Ejemplo

La funci??n cuadrada f (x) = x ?? es diferenciable en x = 3, y su derivada existe 6. Esto se demuestra por escribir el cociente de diferencias de la siguiente manera:

${F (3 + h) -f (3) \ over h} = {(3 + h) ^ 2 - 9 \ over {h}} = {9 + 6h + h ^ 2 - 9 \ over {h}} = {6h + h ^ 2 \ over {h}} = 6 + h.$

Entonces conseguimos la funci??n simplificada en el l??mite:

$\ Lim_ {h \ a 0} 6 + h = 6 + 0 = 6.$

La ??ltima expresi??n muestra que el cociente de diferencias es igual a 6 + h cuando h no es cero y no est?? definido cuando h es cero. (Recuerde que debido a la definici??n del cociente de diferencias, el cociente de diferencias siempre indefinido cuando h es cero.) Sin embargo, no es una forma natural de llenar un valor para el cociente de diferencias en cero, es decir, 6. Por lo tanto la pendiente de la gr??fica de la funci??n de elevaci??n al cuadrado en el punto (3, 9) es 6, y por lo que su derivada en x = 3 es f '(3) = 6.

M??s en general, un c??lculo similar muestra que la derivada de la funci??n de elevaci??n al cuadrado en x = a es f '(a) = 2 a.

Continuidad y diferenciabilidad

Esta funci??n no tiene una derivada en el punto marcado, ya que la funci??n no es continua all??.

Si y = f (x) es diferenciable en a, entonces f tambi??n debe ser continua en a. A modo de ejemplo, elegir un punto a y sea f la funci??n de paso que devuelve un valor, por ejemplo 1, para todos los x menos de una, y devuelve un valor diferente, por ejemplo 10, para todo x mayor que o igual a a. f no puede tener una derivada en a. Si h es negativa, entonces a + h es en la parte baja del paso, por lo que la l??nea secante de A a A + h ser?? muy empinada, y cuando h tiende a cero la pendiente tiende a infinito. Si h es positivo, entonces a + h est?? en la parte alta de la etapa, por lo que la l??nea secante de A a A + h tendr?? pendiente cero. En consecuencia, las l??neas secantes no se acercan a cualquier sola pendiente, por lo que no existe el l??mite del cociente de diferencias.

La funci??n valor absoluto es continua, pero no ser diferenciable en x = 0, ya que tiene una esquina aguda.

Sin embargo, incluso si una funci??n es continua en un punto, puede que no sea diferenciable all??. Por ejemplo, el valor absoluto funci??n y = | x | es continua en x = 0, pero no es diferenciable all??. Si h es positivo, entonces la pendiente de la recta secante de 0 a h es uno, mientras que si h es negativa, entonces la pendiente de la recta secante de 0 a h es uno negativo. Esto se puede ver gr??ficamente como una "torcedura" en el gr??fico en x = 0. Incluso una funci??n con un gr??fico lisa, que no es diferenciable en un punto donde su tangente es vertical: Por ejemplo, la funci??n y = ³ √ x no es diferenciable en x = 0.

La mayor??a de las funciones que se producen en la pr??ctica tienen los derivados en todos los puntos o en casi todos los puntos. Sin embargo, un resultado de Stefan Banach afirma que el conjunto de funciones que tienen un derivado en alg??n momento es una magro aparato en el espacio de todas las funciones continuas. De manera informal, esto significa que las funciones diferenciables son muy at??pica entre funciones continuas. El primer ejemplo conocido de una funci??n que es continua en todas partes pero diferenciable en ninguna parte es la Funci??n de Weierstrass.

El derivado como una funci??n

Sea f una funci??n que tiene un derivado en cada punto a en el dominio de f. Debido a que cada punto A tiene un derivado, hay una funci??n que env??a el punto A a la derivada de f en a. Esta funci??n se escribe f '(x) y se llama la funci??n derivada o la derivada de f. La derivada de f recoge todos los derivados de f en todos los puntos en el dominio de f.

A veces, f tiene una derivada en la mayor??a, pero no todos, los puntos de su dominio. La funci??n cuyo valor en A es igual a f '(a) siempre que f' (a) se define y est?? definido en otra parte es tambi??n llamada la derivada de f. Todav??a es una funci??n, pero su dominio es estrictamente menor que el dominio de f.

El uso de esta idea, la diferenciaci??n se convierte en una funci??n de las funciones: El derivado es una operador cuyo dominio es el conjunto de todas las funciones que tienen derivadas en cada punto de su dominio y cuyo recorrido es un conjunto de funciones. Si denotamos por este operador D, entonces D (f) es la funci??n f '(x). Desde D (f) es una funci??n, que puede ser evaluada en un punto a. Por la definici??n de la funci??n derivada, D (f) (A) = f '(a).

Para la comparaci??n, considere la funci??n de duplicaci??n f (x) = x 2; f es una funci??n real de un n??mero real, lo que significa que se necesita un n??mero como entradas y tiene n??meros como salidas:

$\ Begin {align} 1 & {} \ mapsto 2, \\ 2 & {} \ mapsto 4, 3 \\ & {} \ mapsto 6. \ end {align}$

El operador D, sin embargo, no est?? definido en n??meros individuales. S??lo se define en las funciones de:

$\ Begin {align} D (x \ mapsto 1) y = (x \ mapsto 0), \\ D (x \ mapsto x) y = (x \ mapsto 1), \\ D (x \ mapsto x ^ 2) & = (x \ mapsto 2 \ cdot x). \ End {align}$

Debido a la salida de D es una funci??n, la salida del D puede ser evaluada en un punto. Por ejemplo, cuando D se aplica a la funci??n de elevaci??n al cuadrado,

$x \ mapsto x ^ 2,$

D env??a la funci??n de duplicaci??n,

$x \ mapsto 2x,$

que nombramos f (x). Esta funci??n de salida puede entonces ser evaluada para obtener f (1) = 2, f (2) = 4, y as?? sucesivamente.

Derivados m??s altos

Sea f una funci??n diferenciable, y sea f '(x) su derivada. La derivada de f '(x) (si lo tiene) se escribe f' '(x) y se llama la segunda derivada de f. Del mismo modo, la derivada de una segunda derivada, si existe, se escribe f '' '(x) y se llama la tercera derivada de f. Estos derivados repetidas se llaman derivadas de orden superior.

Una funci??n f no necesita tener un derivado, por ejemplo, si no es continua. Del mismo modo, incluso si f tiene un derivado, puede no tener una segunda derivada. Por ejemplo, dejar

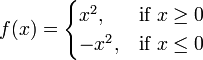$f (x) = \ begin {casos} x ^ 2, y \ mbox {si} x \ ge 0 \\ -x ^ 2, y \ mbox {si} x \ le 0 \ end {casos}$ .

Un c??lculo elemental muestra que f es una funci??n diferenciable cuya derivada es

$f '(x) = \ begin {casos} 2x, y \ mbox {si} x \ ge 0 \\ -2x, & \ mbox {si} x \ le 0 \ end {casos}$ .

f '(x) es el doble de la funci??n de valor absoluto, y no tienen un derivado en cero. Ejemplos similares demostrar que una funci??n puede tener derivados k para cualquier k entero no negativo, pero no (k + 1) -orden derivado. Una funci??n que tiene k derivadas sucesivas se llama k veces diferenciable. Si adem??s el orden k derivada es continua, entonces la funci??n se dice que es de diferenciabilidad clase C ^k. (Esta es una condici??n m??s fuerte que tiene derivados k. Para un ejemplo, v??ase clase diferenciabilidad.) Una funci??n que tiene infinitamente muchos derivados se llama infinitamente diferenciable o liso.

En la recta real, cada funci??n polin??mica es infinitamente diferenciable. Por norma reglas de diferenciaci??n, si un polinomio de grado n se diferencia n veces, entonces se convierte en una funci??n constante. Todas sus derivados posteriores son id??nticamente cero. En particular, existen, por lo polinomios son funciones suaves.

Las derivadas de una funci??n f en un punto x proporcionan aproximaciones polin??micas a esa funci??n cerca de x. Por ejemplo, si f es dos veces diferenciable, entonces

$f (x + h) \ aprox f (x) + f '(x) h + \ tfrac12 f' '(x) h ^ 2$

en el sentido de que

$\ Lim_ {h \ a 0} \ frac {f (x + h) - f (x) - f '(x) h - \ frac12 f' '(x) h ^ 2} {h ^ 2} = 0.$

Si f es infinitamente diferenciable, entonces este es el comienzo de la serie de Taylor para f.

Notaciones para la diferenciaci??n

Notaci??n de Leibniz

La notaci??n para derivados introducidos por Gottfried Leibniz es uno de los primeros. Todav??a se utiliza com??nmente cuando la ecuaci??n y = f (x) es vista como una relaci??n funcional entre variables dependientes e independientes. A continuaci??n, la primera derivada se denota por

$\ Frac {dy} {dx}, \ quad \ frac {df} {dx} (x), \; \; \ mathrm {o} \; \; \ Frac {d} {dx} f (x).$

Derivadas de orden superior se expresan usando la notaci??n

$\ Frac {d ^ ny} {dx ^ n}, \ quad \ frac {d ^ nf} {dx ^ n} (x), \; \; \ mathrm {o} \; \; \ Frac {d ^ n} {dx ^ n} f (x)$

para la n-??sima derivada de y = f (x) (con respecto a x).

Con la notaci??n de Leibniz, podemos escribir la derivada de y en el punto x = a de dos maneras diferentes:

$\ Frac {dy} {dx} \ left {\ \ \ frac {} {}!} \ Right |. _ {X = a} = \ frac {dy} {dx} (a).$

Notaci??n de Leibniz permite especificar la variable de diferenciaci??n (en el denominador). Esto es especialmente relevante para diferenciaci??n parcial. Tambi??n hace que el regla de la cadena f??cil de recordar:

$\ Frac {dy} {dx} = \ frac {dy} {du} \ cdot \ frac {du} {dx}.$

Notaci??n de Lagrange

Una de las notaciones modernas m??s comunes para la diferenciaci??n se debe a Joseph Louis Lagrange y utiliza el Primer marca, f de manera que se denota la derivada de una funci??n f (x) '(x) o simplemente f'. Del mismo modo, el segundo y el tercero derivados se denotan

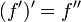$(F ')' = f '' \,$ y $(F '') '= f' '' \ ,.$

M??s all?? de este punto, algunos autores utilizan n??meros romanos como

$f ^ {\ mathrm {iv}} \,$

para la cuarta derivada, mientras que otros autores sit??an el n??mero de derivados entre par??ntesis:

$f ^ {(4)} \,$

Esta ??ltima notaci??n generaliza para dar el f notaci??n ⁽ⁿ⁾ para la en??sima derivada de f - esta notaci??n es m??s ??til cuando se quiere hablar de la derivada como una funci??n en s??, como en este caso la notaci??n de Leibniz puede llegar a ser engorroso.

Notaci??n de Newton

La notaci??n de Newton para la diferenciaci??n, tambi??n llamada la notaci??n de punto, coloca un punto sobre el nombre de funci??n para representar un derivado. Si y = f (t), entonces

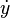$\ Dot {y}$ y $\ Ddot {y}$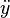

denotan, respectivamente, las primera y segunda derivadas de y con respecto a t. Esta notaci??n se utiliza casi exclusivamente para derivados de tiempo, lo que significa que la variable independiente de la funci??n representa el tiempo . Es muy com??n en la f??sica y en disciplinas matem??ticas relacionadas con la f??sica, como las ecuaciones diferenciales . Mientras la notaci??n se vuelve inmanejable para los derivados de alto orden, en la pr??ctica s??lo se necesitan muy pocos derivados.

Notaci??n de Euler

Euler utiliza la notaci??n 's un operador diferencial D, que se aplica a una funci??n f para dar el derivado de primera Df. La segunda derivada se denota D ² f, y la n-??sima derivado se denota D ⁿ f.

Si y = f (x) es una variable dependiente, a continuaci??n, a menudo el sub??ndice x se une a la D para aclarar la variable x independiente. Notaci??n de Euler se escribe a continuaci??n

$D_X y \,$ o $D_X f (x) \,$ ,

Aunque este sub??ndice se omite a menudo cuando se entiende la variable x, por ejemplo, cuando esta es la ??nica variable presente en la expresi??n.

Notaci??n de Euler es ??til para afirmar y resolver ecuaciones diferenciales lineales.

C??lculo de la derivada

La derivada de una funci??n puede, en principio, se calcula a partir de la definici??n considerando el cociente de diferencias, y calcular su l??mite. Para algunos ejemplos, v??ase Derivados (ejemplos). En la pr??ctica, una vez que se conocen los derivados de algunas funciones sencillas, los derivados de otras funciones se calculan m??s f??cilmente el uso de reglas para la obtenci??n de derivados de funciones m??s complicadas de otras m??s simples.

Derivadas de las funciones elementales

Adem??s, los derivados de algunas funciones comunes son ??tiles para saber.

Los derivados de poderes: si

$f (x) = x ^ r \,$ ,

donde r es cualquier n??mero real , entonces

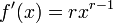$f '(x) = ^ rx \ {r-1},$ ,

donde esta funci??n se define. Por ejemplo, si r = 1/2, entonces

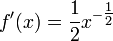$f '(x) = \ frac {1} {2} x ^ {- \ tfrac12} \,$ .

y la funci??n se define s??lo para x no negativo. Cuando r = 0, esta regla se recupera la regla constante.

Exponenciales y logar??tmicas funciones:

$\ Frac {d} {dx} e ^ x = e ^ x$

$\ Frac {d} {dx} a ^ x = \ ln (a) a ^ x$

$\ Frac {d} {dx} \ ln (x) = 1 / x, \ qquad x> 0$

$\ Frac {d} {dx} \ log_a (x) = \ frac {1} {x \ ln (a)}$

Funciones trigonom??tricas :

$\ Frac {d} {dx} \ sin (x) = \ cos (x).$

$\ Frac {d} {dx} \ cos (x) = - \ sin (x).$

$\ Frac {d} {dx} \ tan (x) = \ s ^ 2 (x).$

Funciones trigonom??tricas inversas:

$\ Frac {d} {dx} \ arcsin (x) = \ frac {1} {\ sqrt {1-x ^ 2}}.$

$\ Frac {d} {dx} \ arccos (x) = - \ frac {1} {\ sqrt {1-x ^ 2}}.$

$\ Frac {d} {dx} \ arctan (x) = \ frac {1} {{1 + x ^ 2}}.$

Reglas para la b??squeda de la derivada

En muchos casos, los c??lculos de l??mite complicados por aplicaci??n directa de la diferencia de cociente de Newton se pueden evitar utilizando las reglas de diferenciaci??n. Algunas de las reglas m??s b??sicas son las siguientes.

Constant regla: si f (x) es constante, entonces

$f '= 0 \,$

Regla Suma:

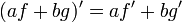$(Af + bg) '= af' + bg '\,$ para todas las funciones f y g y todos los n??meros reales a y b.

Estado del producto:

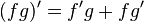$(Fg) '= f' g + fg '\,$ para todas las funciones f y g.

Regla del cociente:

$\ Left (\ frac {f} {g} \ right) '= \ frac {f'g - fg'} {g ^ 2}$

Regla de la cadena: Si 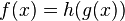$f (x) = h (g (x))$ , A continuaci??n,

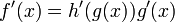$f '(x) = h' (g (x)) g '(x) \,$ .

Ejemplo de c??lculo

El derivado de

$f (x) = x ^ 4 + \ sin (x ^ 2) - \ ln (x) e ^ x + 7 \,$

$\ Begin {align} f '(x) y = 4 x ^ {(4-1)} + \ frac {d \ left (x ^ 2 \ right)} {dx} \ cos (x ^ 2) - \ frac {d \ left (\ ln {x} \ right)} {dx} e ^ x - \ ln {x} \ frac {d \ left (e ^ x \ right)} {dx} + 0 \\ & = 4x ^ 3 + 2x \ cos (x ^ 2) - \ frac {1} {x} e ^ x - \ ln (x) e ^ x. \ End {align}$

Aqu?? el segundo t??rmino se calcula utilizando la regla de la cadena y tercero utilizando la regla del producto: los derivados conocidos de las funciones elementales x ??, x ^4, sin (x), ln (x) y exp (x) = tambi??n se utilizaron e ^x .

Derivados en dimensiones superiores

Derivados de funciones vectoriales valorado

La funci??n y vector de valor (t) de una variable real es una funci??n que env??a los n??meros reales a los vectores en alg??n espacio vectorial R ^n. Una funci??n vectorial se puede dividir en sus funciones coordinar y ₁ (t), y ₂ (t), ..., y _n (t), lo que significa que y (t) = (y ₁ (t), ... , y _n (t)). Esto incluye, por ejemplo, curvas param??tricas en ^R2 o ^R3. Las funciones de coordenadas son reales funciones valorados, por lo que la anterior definici??n de derivado se aplica a ellos. El derivado de y (t) se define como el vector , llamado vector tangente, cuyas coordenadas son las derivadas de las funciones de coordenadas. Esto es,

$\ Mathbf {y} '(t) = (y'_1 (t), \ ldots, y'_n (t)).$

De manera equivalente,

$\ Mathbf {y} '(t) = \ lim_ {h \ a 0} \ frac {\ mathbf {y} (t + h) - \ mathbf {y} (t)} {h},$

si existe el l??mite. La resta en el numerador es la resta de vectores, no escalares. Si existe la derivada de y para cada valor de t, entonces y 'es otra funci??n vectorial valorado.

Si e _1, ..., e _n es la base est??ndar para R ^n, entonces y (t) tambi??n se puede escribir como _y1 (t) e ₁ + ... + y _n (t) _e s. Si asumimos que la derivada de una funci??n vectorial conserva la propiedad de linealidad, a continuaci??n, la derivada de y (t) debe ser

$y'_1 (t) \ mathbf {e} _1 + \ cdots + y'_n (t) \ mathbf {e} _n$

porque cada uno de los vectores de la base es una constante.

Esta generalizaci??n es ??til, por ejemplo, si y (t) es el vector de posici??n de una part??cula en el tiempo t; entonces la derivada y '(t) es la velocidad del vector de la part??cula en el tiempo t.

Derivadas parciales

Supongamos que f es una funci??n que depende de m??s de una variable. Por ejemplo,

$f (x, y) = x ^ 2 + xy + y ^ 2. \,$

f puede ser reinterpretado como una familia de funciones de una variable indexada por las otras variables:

$f (x, y) = f_x (y) = x ^ 2 + xy + y ^ 2. \,$

En otras palabras, cada valor de x elige una funci??n, denotado f _x, que es una funci??n de un n??mero real. Esto es,

$x \ mapsto f_x, \,$

$f_x (y) = x ^ 2 + xy + y ^ 2. \,$

Una vez que se elige un valor de x, decir a, entonces f (x, y) determina una funci??n f _a la cual Y env??a a un ?? + ay + y ??:

$f_a (y) = a ^ 2 + ay + y ^ 2. \,$

En esta expresi??n, a es una constante, no una variable, por lo que _un f es una funci??n de una sola variable real. En consecuencia, la definici??n de la derivada de una funci??n de una variable se aplica:

$f_a '(y) = a 2y +. \,$

El procedimiento anterior se puede realizar para cualquier elecci??n de a. Montaje de los derivados juntos en una funci??n da una funci??n que describe la variaci??n de f en la direcci??n y:

$\ Frac {\ part f} {\ part y} (x, y) = x + 2y.$

Esta es la derivada parcial de f con respecto a y. Aqu?? ∂ es una d redondeada llama el s??mbolo de derivada parcial. Para distinguirla de la letra d, ∂ a veces se pronuncia "der", "del" o "parcial" en lugar de "dee".

En general, la derivada parcial de una funci??n f (x _1, ..., x _n) en la direcci??n x _i en el punto (a ₁ ..., a _n) se define como:

$\ Frac {\ part f} {\ part x_i} (a_1, \ ldots, a_n) = \ lim_ {h \ a 0} \ frac {f (a_1, \ ldots, a_i + h, \ ldots, a_n) - f (a_1, \ ldots, a_n)} {h}.$

En el cociente de diferencias anteriormente, todas las variables, excepto x _i se mantiene fijo. Esta elecci??n de valores fijos determina una funci??n de una variable

$F_ {a_1, \ ldots, a_ {i-1}, a_ {i + 1}, \ ldots, a_n} (x_i) = f (a_1, \ ldots, a_ {i-1}, x_i, a_ {i + 1}, \ ldots, a_n)$

y, por definici??n,

$\ Frac {df_ {a_1, \ ldots, a_ {i-1}, a_ {i + 1}, \ ldots, a_n}} {} dx_i (a_1, \ ldots, a_n) = \ frac {\ part f} { \ parte x_i} (a_1, \ ldots, a_n).$

En otras palabras, las diferentes opciones de un ??ndice de una familia de funciones de una variable igual que en el ejemplo anterior. Esta expresi??n tambi??n muestra que el c??lculo de las derivadas parciales reduce al c??lculo de los derivados de una variable.

Un ejemplo importante de una funci??n de varias variables es el caso de una funci??n f con valores escalares (x _1, ... x _n) en un dominio en el espacio euclidiano R ⁿ (por ejemplo, en I o R ?? ??). En este caso f tiene una derivada parcial f ∂ / ∂ x _j con respecto a cada x _j variable. En el punto a, estas derivadas parciales definen el vector

$\ Nabla f (a) = \ left (\ frac {\ f parcial} {\ x_1 parcial} (a), \ ldots, \ frac {\ f parcial} {\ x_n parcial} (a) \ right).$

Este vector se llama gradiente de f en a. Si f es diferenciable en cada punto en alg??n dominio, entonces el gradiente es una funci??n f ∇ vector de valor que tiene el punto a al vector ∇ f (a). En consecuencia, el gradiente determina una campo vectorial.

Derivadas direccionales

Si f es una funci??n de valor real en R ^n, entonces las derivadas parciales de medida f su variaci??n en la direcci??n de los ejes de coordenadas. Por ejemplo, si f es una funci??n de x e y, a continuaci??n, sus derivadas parciales miden la variaci??n de f en la direcci??n x y la direcci??n y. Ellos no, sin embargo, medir directamente la variaci??n de f en cualquier otra direcci??n, tal como a lo largo de la diagonal recta y = x. Estos se miden utilizando derivadas direccionales. Elige un vector

$\ Mathbf {v} = (v_1, \ ldots, v_n).$

La derivada direccional de f en la direcci??n de v en el punto x es el l??mite

$D _ {\ mathbf {v}} {f} (\ boldsymbol {x}) = \ lim_ {h \ rightarrow 0} {\ frac {f (\ boldsymbol {x} + h \ mathbf {v}) - f (\ boldsymbol {x})} {h}}.$

Vamos λ sea un escalar. La sustituci??n de h / λ para h cambia diferencia cociente del λ v de direcci??n en tiempos λ diferencia de cociente la v de direcci??n. En consecuencia, la derivada direccional en la direcci??n λ v es λ veces la derivada direccional en la direcci??n v. Debido a esto, derivadas direccionales a menudo se consideran s??lo para vectores unitarios v.

Si existen todas las derivadas parciales de f y son continuas en x, entonces determinar la derivada direccional de f en la direcci??n v por la f??rmula:

$D _ {\ mathbf {v}} {f} (\ boldsymbol {x}) = \ sum_ {j = 1} ^ n v_j \ frac {\ f parcial} {\ x_j parcial}.$

Esto es una consecuencia de la definici??n de la derivada total. Se deduce que la derivada direccional es lineal en v.

La misma definici??n tambi??n funciona cuando f es una funci??n con valores en R ^m. Nos limitamos a usar la definici??n anterior en cada componente de los vectores. En este caso, la derivada direccional es un vector en R ^m.

La derivada total, el diferencial total y el Jacobiano

Sea f una funci??n de un dominio de R a R. La derivada de f en un punto A en su dominio es la mejor aproximaci??n lineal a f en ese punto. Como anteriormente, este es un n??mero. Geom??tricamente, si v es un vector unitario a partir de a, entonces f '(a), la mejor aproximaci??n lineal de f en A, debe ser la longitud del vector encontrado moviendo v para el espacio objetivo usando f. (Este vector se llama pushforward de v por f y por lo general se escribe 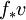$f_ * v$ .) En otras palabras, si v se mide en t??rminos de distancias en el objetivo, entonces, porque v s??lo puede medirse a trav??s de f, v ya no parece ser un vector unitario porque f no conserva vectores unitarios. En lugar v parece tener longitud f '(a). Si m es mayor que uno, entonces escribiendo f usando coordinar las funciones, la longitud de v en cada una de las direcciones de coordenadas se puede medir por separado.

Supongamos ahora que f es una funci??n de un dominio R en ⁿ a R ^m y que a es un punto en el dominio de f. La derivada de f en una todav??a debe ser la mejor aproximaci??n lineal a f en a. En otras palabras, si v es un vector en R ^n, entonces f '(a) debe ser el transformaci??n lineal que mejor aproxima f. La transformaci??n lineal debe contener toda la informaci??n acerca de c??mo f transforma vectores en una de vectores en f (a), y en los s??mbolos, esto significa que debe ser la transformaci??n lineal f '(a) tal que

$\ Lim_ {|| \ mathbf {h} || \ rightarrow 0} \ frac {|| f (\ mathbf {a} + \ mathbf {h}) - f (\ mathbf {a}) - f '(\ mathbf {a}) \ mathbf {h}} {|| || \ mathbf {h}} || = 0.$

Aqu?? h es un vector en R ^n, por lo que la norma en el denominador es la longitud est??ndar en R ^n. Sin embargo, f '(a) h es un vector en R ^m, y la norma en el numerador es la longitud est??ndar en R ^m. La transformaci??n lineal f '(a), si existe, se llama la derivada total de f en una o la (total) diferencial de f en a.

Si existe la derivada total en a, entonces existen todas las derivadas parciales de f en a. Si escribimos f usando coordinar las funciones, de manera que f = (f _1, f _2, ..., f _m), entonces la derivada total puede ser expresado como una matriz de llamada Matriz jacobiana de f en un:

$f '(\ mathbf {a}) = \ text {} Jac _ {\ mathbf {a}} = \ left (\ frac {\ f_i parcial} {\ x_j parcial} \ right) _ {ij}.$

La existencia de la Jacobiana es estrictamente m??s fuerte que la existencia de todas las derivadas parciales, pero si existen las derivadas parciales y satisfacen las condiciones de suavidad suaves, entonces existe la derivada total y est?? dada por el Jacobiano.

La definici??n de la derivada total subsume la definici??n de la derivada de una variable. En este caso, existe la derivada total si y s??lo si existe el derivado de costumbre. La matriz Jacobiana reduce a una matriz de 1 ?? 1 cuya entrada s??lo es la derivada f '(x). Esta 1 ?? 1 matriz satisface la propiedad de que f (a + h) - f (a) - f '(a) h es aproximadamente cero, en otras palabras, que

$f (a + h) \ aprox f (a) + f '(a) h.$

Hasta las variables cambiantes, esto es la afirmaci??n de que la funci??n de 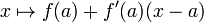$x \ mapsto f (a) + f '(a) (x-a)$ es la mejor aproximaci??n lineal de f en a.

El derivado total de una funci??n no da otra funci??n de la misma manera que el caso de una sola variable. Esto es porque la derivada total de una funci??n multivariable tiene que grabar mucha m??s informaci??n que la derivada de una funci??n de una sola variable. En cambio, la derivada total da una funci??n de la paquete de la tangente de la fuente hasta el fibrado tangente de la meta.

Las generalizaciones

El concepto de un derivado se puede extender a muchas otras configuraciones. El hilo com??n es que la derivada de una funci??n en un punto sirve como aproximaci??n lineal de la funci??n en ese punto.

Un importante generalizaci??n de las preocupaciones derivados complejos funciones de variables complejas, como las funciones de (un dominio en) los n??meros complejos C a C. La noci??n de la derivada de una funci??n de este tipo se obtiene mediante la sustituci??n de las variables reales con variables complejas en la definici??n. Sin embargo, esta definici??n inocente esconde algunas propiedades muy profundas. Si C se identifica con R ?? escribiendo un n??mero complejo z como x + i y, a continuaci??n, una funci??n diferenciable de C a C es ciertamente diferenciable como una funci??n de R a R ?? ?? (en el sentido de que existen todas sus derivadas parciales) , pero lo contrario no es cierto en general: el complejo derivado s??lo existe si el verdadero derivado es lineal complejo y esto impone las relaciones entre las derivadas parciales llamado Ecuaciones de Cauchy Riemann - ver funciones holomorfas.

Otra generalizaci??n se refiere a las funciones entre variedades diferenciables o lisas. Intuitivamente hablando una variedad M tal es un espacio que puede ser aproximado cerca de cada punto x por un espacio vectorial llamado su espacio tangente: el ejemplo protot??pico es un superficie lisa en I ??. El derivado (o diferencial) de un (diferenciable) f: M → N entre colectores, en un punto x en M, es entonces un mapa lineal desde el espacio tangente de M en x para el espacio tangente de N en f (x). La funci??n derivada se convierte en un mapa entre el paquetes tangentes de M y N. Esta definici??n es fundamental en geometr??a diferencial y tiene muchos usos - ver pushforward (diferencial) y pullback (geometr??a diferencial).

La diferenciaci??n tambi??n se puede definir para los mapas entre dimensionales infinitos espacios vectoriales como Espacios de Banach y Espacios de Fr??chet. No es una generalizaci??n tanto de la derivada direccional, llamado Derivado G??teaux, y de la diferencia de, llamado el Derivada de Fr??chet.

Una deficiencia del derivado cl??sica es que no muchas funciones son diferenciables. Sin embargo, hay una manera de extender la noci??n del derivado de modo que todos funciones continuas y muchas otras funciones pueden diferenciarse utilizando un concepto conocido como la derivado d??bil. La idea es la de insertar las funciones continuas en un espacio m??s grande llamado el espacio de distribuciones y s??lo requieren que una funci??n es diferenciable "en promedio".

Las propiedades de la derivada han inspirado la introducci??n y estudio de muchos objetos similares en el ??lgebra y la topolog??a - ver, por ejemplo, ??lgebra diferencial.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Derivative&oldid=198886698 "