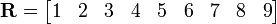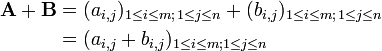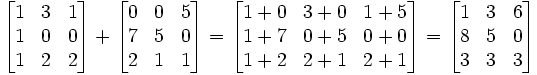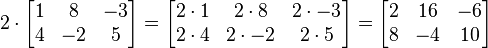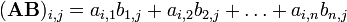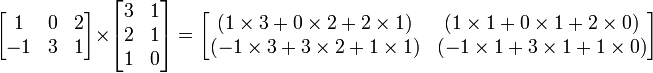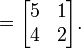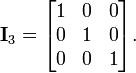Matriz (matemáticas)

Temas relacionados: Matemáticas

Antecedentes de las escuelas de Wikipedia

SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Antes de decidir sobre el patrocinio de un niño, ¿por qué no aprender sobre diferentes obras de caridad de patrocinio primero ?

En matemáticas , una matriz (matrices plural) es una mesa rectangular de elementos (o entradas), que pueden ser números o, más generalmente, cualquier cantidades abstractas que se pueden agregar y se multiplicaba. Las matrices se utilizan para describir ecuaciones lineales , no perder de vista el coeficientes de transformaciones lineales y para registrar los datos que dependen de varios parámetros. Las matrices se describen por el campo de la teoría de la matriz . Las matrices se pueden agregar, se multiplicaron y descompuestos de diversas maneras, lo que también les hace un concepto clave en el campo de álgebra lineal .

En este artículo, las entradas de una matriz son reales o complejos números a menos que se indique lo contrario.

Organización de una matriz

Definiciones y notaciones

Las líneas horizontales en una matriz se llaman filas y las líneas verticales se llaman columnas. Una matriz con m filas y n columnas se llama (m × n escrito) m -by- n matriz y m y n son llamados sus dimensiones. Las dimensiones de una matriz siempre se dan con el número de filas primera, a continuación, el número de columnas. Comúnmente se dice que una matriz -by- n m tiene un orden de m × n ("orden", es decir el tamaño). Dos matrices del mismo orden cuyas entradas correspondiente son equivalentes se consideran iguales.

Casi siempre mayúsculas denotan las matrices con las correspondientes letras minúsculas con dos índices que representan las entradas. Por ejemplo, la entrada de una matriz A que se encuentra en la fila i-ésima y la j-ésima columna se escribe como una _{i, j} y llamaron a la i, j de entrada o (i, j) -ésimo entrada de A. Notaciones alternativas para que la entrada es a [i, j] o A _{i, j.} La fila siempre se observa en primer lugar, a continuación, la columna. En este ejemplo, A (sin subíndices) simbolizaría toda la matriz. Además de usar las letras mayúsculas como símbolos que representan matrices, muchos autores utilizan un estilo tipográfico especial, comúnmente negrita en posición vertical (no en cursiva), para distinguir aún más matrices de otras variables. A raíz de este convenio, A es una matriz, que se distingue de la A, un escalar. Una convención alternativa es anotar matrices con sus dimensiones en letra pequeña debajo del símbolo, por ejemplo, 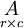$\ r \ {underset veces c} {A}$ para una matriz r -by- c.

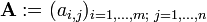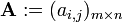A menudo escribimos $\ Mathbf {A}: = (a_ {i, j}) _ {i = 1, \ ldots, m; \, \, j = 1, \ ldots, n}$ o $\ Mathbf {A}: = (a_ {i, j}) _ {m \ times n}$ para definir una matriz m × n A. En este caso, las entradas a _{i, j} se definen por separado para todos los enteros 1 ≤ i ≤ m y 1 ≤ j ≤ n. En algunos lenguajes de programación, la numeración de filas y columnas comienza en cero. Textos que utilizan dicha lengua ampliamente, con frecuencia seguir esa convención, así que tenemos 0 ≤ i ≤ m -1 y 0 ≤ j ≤ n -1.

Una matriz en donde una de las dimensiones es igual a uno a menudo se llama un vector, y se interpreta como un elemento de espacio de coordenadas reales . Un m × (filas una columna y m) 1 de la matriz se llama vector columna y una matriz n × 1 (una fila y n columnas) se llama vector fila.

Definición matemática

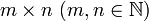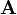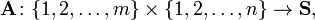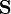Una $\, M \ times n \, \, (m, n \ in \ mathbb {N})$ matriz $\ Mathbf {A} \,$ es una función de $\ Mathbf {A} \ puntos \ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \ a \ mathbf {S}, \, \,$ donde $\ Mathbf {S} \,$ es cualquier no- conjunto vacío.

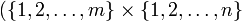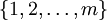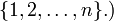
$(\ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \,$ es el Producto cartesiano de conjuntos $\ {1, 2, \ ldots, m \} \,$ y $\ {1, 2, \ ldots, n \}.) \,$

Decimos que la matriz 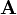$\ Mathbf {A}$ es una matriz sobre el conjunto 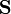$\ Mathbf {S}$ . Lo importante a destacar es que, si queremos tener álgebra de matrices, el conjunto 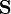$\ Mathbf {S} \,$ debe ser una anillo y la matriz 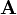$\ Mathbf {A}$ debe ser una matriz cuadrada (ver matrices cuadradas y definiciones relacionados a continuación para obtener una explicación más detallada). Dado que el conjunto de todas las matrices cuadradas sobre un anillo es también un anillo, álgebra de matrices generalmente se llama anillo de matriz.

Dado que este artículo considera principalmente matrices sobre los números reales , las matrices que se muestran aquí son en realidad funciones 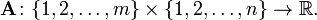$\ Mathbf {A} \ puntos \ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \ a \ mathbb {R}. \, \,$

Ejemplo

La matriz

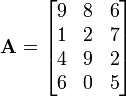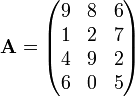
$\ Mathbf {A} = \ begin {} bmatrix 9 y 8 y 6 \\ 1 & 2 y 7 \\ 4 y 9 y 2 \\ 6 y 0 y 5 \ end {bmatrix}$ o $\ Mathbf {A} = \ begin {pmatrix} 9 y 8 y 6 \\ 1 & 2 y 7 \\ 4 y 9 y 2 \\ 6 y 0 y 5 \ end {pmatrix}$

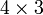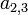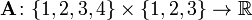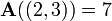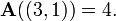
es un $4 \ 3 veces$ matriz. El elemento $a_ {2,3}$ o $\ Mathbf {A} [2,3]$ es 7. En términos de la definición matemática dada anteriormente, esta matriz es una función de $\ Mathbf {A} \ puntos \ {1, 2, 3, 4 \} \ times \ {1, 2, 3 \} \ a \ mathbb {R} \,$ y, por ejemplo, $\ Mathbf {A} ((2, 3)) = 7 \,$ y $\ Mathbf {A} ((3, 1)) = 4. \,$

La matriz

$\ Mathbf {R} = \ begin {bmatrix} 1 & 2 & 3 & 4 y 5 & 6 & 7 & 8 & 9 \ end {bmatrix}$

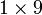es un $1 \ 9 veces$ matriz o 9-elemento vector fila.

Sumar y multiplicar matrices

Suma

Dos o más matrices de dimensiones idénticas M y n pueden ser añadidos. M -by- n matrices Dada A y B, su suma A + B es la matriz m -by- n calculada sumando los elementos correspondientes:

$\ Begin {align} \ mathbf {A} + \ vec {B} & = (a_ {i, j}) _ {1 \ le i \ le m; \, 1 \ le j \ le n} + (b_ { i, j}) _ {1 \ le i \ le m; \, 1 \ le j \ le n} \\ & = (a_ {i, j} + b_ {i, j}) _ {1 \ le i \ le m; 1 \ le j \ le n} \\ \ end {align}$

Por ejemplo:

$\ Begin {bmatrix} 1 & 3 & 1 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \ end {bmatrix} + \ begin {bmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \ end {bmatrix} = \ begin {bmatrix} 1 + 0 y 3 + 0 y 1 + 5 + 7 \\ 1 y 0 + 5 y 0 + 0 \\ 1 + 2 y 2 + 1 y 2 1 \ end {bmatrix} = \ begin {bmatrix} 1 y 3 y 6 \\ 8 y 5 y 0 \\ 3 & 3 & 3 \ end {bmatrix}$

Otra idea, que se utiliza con mucha menos frecuencia de la suma de matrices es la suma directa.

Multiplicación escalar

Dada una matriz A y un número c, la la multiplicación escalar c A se calcula multiplicando cada elemento de A por la escalar c (es decir, 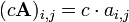$(C \ mathbf {A}) _ {i, j} = c \ cdot a_ {i, j}$ ). Por ejemplo:

$2 \ cdot \ begin {bmatrix} 1 y 8 y -3 \\ 4 y -2 y 5 \ end {bmatrix} = \ begin {bmatrix} 2 \ cdot 1 y 2 \ cdot 8 y 2 \ cdot -3 \\ 2 \ cdot 4 y 2 \ cdot -2 y 2 \ cdot 5 \ end {bmatrix} = \ begin {bmatrix} 2 y 16 y -6 \\ 8 y -4 y 10 \ end {bmatrix}$

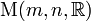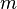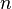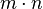Además Matrix y multiplicación escalar gire el conjunto $\ Text {H} (m, n, \ mathbb {R})$ de todo $m$ -by- $n$ matrices con verdaderas entradas en un verdadero espacio vectorial de dimensión $m \ cdot n$ .

La multiplicación de matrices

La multiplicación de dos matrices está bien definido sólo si el número de columnas de la matriz de la izquierda es el mismo que el número de filas de la matriz de la derecha. El punto medio ( $\ Cdot$ ) No se utiliza para indicar la multiplicación de matrices (que se utiliza para la multiplicación escalar). Si A es una matriz m -by- n y B es una matriz de n -by- p, entonces su producto AB es la matriz m -by- matriz de p dada por:

$(\ Mathbf {AB}) _ {i, j} = a_ {i, 1} b_ {1, j} + a_ {i, 2} b_ {2, j} + \ ldots + a_ {i, n} b_ {n, j}$

para cada par 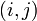$(I, j)$ . Por ejemplo:

$\ Begin {bmatrix} 1 & 0 & 2 \\ -1 y 3 & 1 \\ \ end {bmatrix} \ times \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \\ \ end { bmatrix} = \ begin {bmatrix} (1 \ épocas 3 + 0 \ Tiempos 2 + 2 \ veces 1) y (1 \ Tiempos 1 + 0 \ Tiempos 1 + 2 \ épocas 0) \\ (-1 \ veces 3 + 3 \ Tiempos 2 + 1 \ Tiempos 1) y (-1 \ Tiempos 1 + 3 \ Tiempos 1 + 1 \ Tiempos 0) \\ \ end {bmatrix}$

$= \ Begin {bmatrix} 5 y 1 \\ 4 y 2 \\ \ end {bmatrix}.$

La multiplicación de matrices tiene las siguientes propiedades:

(AB) C = A (BC) para todo k -by- m matrices A, m -by- n matrices B y n -by- matrices p C ("asociatividad").
(A + B) C = AC + BC para todo m -by- n matrices A y B yn -by- matrices k C ("distributividad derecho").
C (A + B) = CA + CB para todo m -by- n matrices A y B y K -by- m matrices C ("distributividad izquierda").

La multiplicación de matrices no es conmutativa ; es decir, dado matrices A y B y su producto definido, entonces generalmente AB 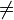$\ Ne$ BA. También puede suceder que AB está definido, pero BA no está definido.

Además de la multiplicación de la matriz ordinaria se acaba de describir, existen otras operaciones en matrices que se pueden considerar formas de multiplicación, como el producto Hadamard y de la Producto de Kronecker.

Transformaciones lineales, clasifica y transponer

Las matrices pueden representar convenientemente transformaciones lineales porque la multiplicación matriz corresponde perfectamente a la composición de mapas, como se describe a continuación. Esta misma propiedad los convierte en las estructuras de datos de gran alcance en los lenguajes de programación de alto nivel.

Aquí y en la secuela identificamos R ⁿ con el conjunto de "columnas" o n-1 -por matrices. Por cada mapa lineal f: ^Rn → R ^m existe una m única -by- n matriz A tal que f (x) = Ax para todo x en R ^n. Decimos que la matriz A "representa" el mapa f lineal. Ahora bien, si el k -by- matriz m B representa otro mapa lineal g: R → R ^{m k,} entonces el mapa lineal g o f está representado por BA. Esto se deduce de la asociatividad de multiplicación de la matriz anteriormente mencionada.

Más en general, un mapa lineal de un espacio vectorial n-dimensional a un espacio de vector dimensional m está representado por una matriz de m -by- n, siempre que bases han sido elegidos para cada uno.

La rango de una matriz A es el dimensión de la imagen del mapa lineal representado por A; esta es la misma que la dimensión del espacio generado por las filas de A, y también la misma que la dimensión del espacio generado por las columnas de A. También puede ser definido sin referencia a álgebra lineal como sigue: el rango de una m -by- matriz n A es el número más pequeño k tal que A se puede escribir como un producto BC donde B es una matriz de m -by- k y C es la matriz n un k -by- (aunque esto no es una forma práctica para calcular el rango).

La transpuesta de una matriz de m -by- n A es el n -by- m matriz A ^tr (también escrito a veces como A o ^{T t} A) formado girando filas en columnas y columnas en filas, es decir, A ^tr [i, j] = A [j, i] para todos los índices i y j. Si A describe un mapa lineal con respecto a dos bases, a continuación, la matriz A ^tr describe la transpuesta del mapa lineal con respecto a las bases dobles, ver espacio dual.

Tenemos (A + B) ^tr = A + B ^{tr tr} y (AB) ^tr = B ^tr A ^tr.

Matrices cuadradas y definiciones relacionados

Una matriz es una matriz cuadrada que tiene el mismo número de filas y columnas. El conjunto de todos los cuadrados n -by- n matrices, junto con la adición de la matriz y la multiplicación de matrices es una anillo. A menos que n = 1, este anillo no es conmutativa .

M (n, R), el anillo de las matrices cuadradas reales, es un unitario de bienes álgebra asociativa. M (n, C), el anillo de las matrices cuadradas complejas, es un complejo de álgebra asociativa.

La matriz de unidad o matriz de identidad I _n, con elementos de la principal conjunto diagonal a 1 y todos los demás elementos establecidos en 0, satisface MI _n = M y E _n N = N para cualquier m -by- n matriz M y n -by- k matriz N. Por ejemplo, si n = 3:

$\ Mathbf {I} _3 = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}.$

La matriz de identidad es el elemento de identidad en el anillo de las matrices cuadradas.

Elementos invertibles en este anillo se denominan matrices invertibles o matrices no singulares. Una matriz N por N A es invertible si y sólo si existe una matriz B tal que

AB = I _n (= BA).

En este caso, B es el matriz inversa de A, denotado por A ^-1. El conjunto de todas las matrices invertibles n -by- n forma un grupo (específicamente un Grupo de Lie) bajo la multiplicación de matrices, la grupo lineal general.

Si λ es un número y v es un vector no nulo tal que Av = λ v, entonces llamamos v Un vector propio de A y λ la asociada valor propio . (Eigen significa "propietario" en alemán y en holandés .) El número λ es un valor propio de A si y sólo si A -λ E _n no es invertible, lo que ocurre si y sólo si p _A (λ) = 0. Aquí p _A (x) es la polinomio característico de A. Este es un polinomio de grado n y tiene, por tanto, n raíces complejas (contando raíces múltiples de acuerdo con su multiplicidad). En este sentido, cada matriz cuadrada tiene valores propios complejos n.

El determinante de una matriz cuadrada A es el producto de sus n valores propios, pero también puede ser definido por el Fórmula de Leibniz. Matrices invertibles son precisamente esas matrices con un determinante distinto de cero.

La eliminación de Gauss algoritmo es de vital importancia: se puede utilizar para calcular determinantes, rangos y inversas de matrices y para resolver sistemas de ecuaciones lineales .

La traza de una matriz cuadrada es la suma de las entradas de la diagonal, lo que equivale a la suma de sus valores propios n.

Exponencial Matrix se define para matrices cuadradas, utilizando series de potencias .

Tipos especiales de matrices

En muchas áreas de las matemáticas, matrices con cierta estructura surgen. Algunos ejemplos importantes son

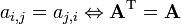Matrices simétricas son tales que los elementos simétrica respecto a la diagonal principal (de la parte superior izquierda a la parte inferior derecha) son iguales, es decir, $a_ {i, j} = a_ {j, i} \ leftrightarrow \ mathbf {A} ^ \ mathrm {T} = \ mathbf {A}$ .
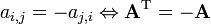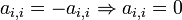Matrices antisimétrica son tales que los elementos simétrica respecto a la diagonal principal son el negativo de la otra, es decir, $a_ {i, j} = - a_ {j, i} \ leftrightarrow \ mathbf {A} ^ \ mathrm {T} = - \ mathbf {A}$ . En una matriz antisimétrica, todos los elementos de la diagonal son cero, es decir, $a_ {i, i} = - a_ {i, i} \ Rightarrow a_ {i, i} = 0$ .
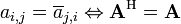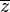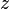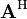Hermitianas (o auto-adjuntos) matrices son tales que los elementos simétricos sobre la diagonal son cada uno de los demás complejos conjugados, es decir, $a_ {i, j} = \ overline {a} _ {j, i} \ leftrightarrow \ mathbf {A} ^ \ mathrm {H} = \ mathbf {A}$ , Donde $\ Overline {z}$ significa el complejo conjugado de un número complejo $z$ y $\, \! \ Mathbf {A} ^ \ mathrm {H}$ la conjugada transpuesta de A.
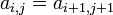Matrices de Toeplitz tienen elementos comunes en sus diagonales, es decir, $\, \! a_ {i, j} = a_ {i + 1, j + 1}$ .
Matrices estocásticos son matrices cuadradas cuyas filas son vectores de probabilidad; que se utilizan para definir Cadenas de Markov.
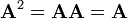Una matriz cuadrada A se llama idempotente si $\ Mathbf {A} ^ 2 = \ mathbf {AA} = \ mathbf {A}$ .

Para una lista más extensa ver lista de matrices.

Matrices en álgebra abstracta

Si partimos de una anillo R, podemos considerar el conjunto M (m, n, R) de todos los m por n matrices con entradas en R. La adición y la multiplicación de estas matrices pueden ser definidos como en el caso de matrices reales o complejos (véase más arriba ). El conjunto M (n, R) de todo n cuadrado por n matrices de más de R es un anillo en su propio derecho, isomorfo al anillo endomorfismo de la R a la izquierda - módulo R ^n.

Del mismo modo, si las entradas se toman de una semiring S, adición y multiplicación de la matriz todavía se pueden definir como de costumbre. El conjunto de todas las n cuadrado × n matrices de más de S es en sí mismo un semiring. Tenga en cuenta que los algoritmos de multiplicación de matriz rápido como el Strassen algoritmo general sólo se aplica a las matrices sobre los anillos y no funcionará para las matrices sobre semirings que no son anillos.

Si R es un anillo conmutativo , entonces M (n, r) es un unitaria álgebra asociativa sobre R. Es entonces también significativo para definir el factor determinante de las matrices cuadradas utilizando el Fórmula de Leibniz; una matriz es invertible si y sólo si su determinante es invertible en R.

Todas las declaraciones mencionadas en este artículo para matrices reales o complejos siguen siendo correcta para matrices más de una arbitraria campo.

Matrices más de una anillo de polinomios son importantes en el estudio de la teoría de control .

Matrices sin entradas

Una pregunta sutil que casi nunca se plantea es si hay una cosa tal como una matriz de 3 por 0. Eso sería una matriz con 3 filas, pero sin ningún tipo de columnas, lo que parece absurdo. Sin embargo, si se quiere ser capaz de tener matrices para todos los mapas lineales entre espacios vectoriales de dimensión finita, se necesita este tipo de matrices, ya que no hay nada malo con mapas lineales de un espacio 0-dimensional a un espacio de 3 dimensiones (de hecho si los espacios están fijados allí es uno de tales mapa, el mapa cero). Así que uno es llevado a admitir que hay exactamente un 3 por 0 matriz (que tiene 3 × 0 = 0 entradas; entradas no nulas pero ninguno en absoluto). Del mismo modo hay matrices con un número positivo de columnas pero no filas. Además, incluso en ausencia de entradas, uno debe todavía seguir la pista del número de filas y columnas, ya que el producto BC donde B es la matriz de 3 por 0 y C es una matriz 0-por-4 es un perfectamente normal 3 -por-4 matriz, cuyos 12 entradas son 0 (ya que se dan por una suma vacío). Tenga en cuenta que este cálculo de BC justifica el criterio dado anteriormente para el rango de una matriz en términos de posibles expresiones como un producto: la matriz de 3 por 4 con cero entradas ciertamente tiene rango 0, por lo que debe ser el producto de un 3 -por-0 de la matriz y una matriz 0-por-4. Para permitir y distinguir entre matrices sin entradas, matrices formalmente deberían definirse, en un estilo de informática poco pedante, como cuádruples (A, R, C, M), donde A es el conjunto en el que las entradas viven, r y c son los números (naturales) de filas y columnas, y M es la colección rectangular de elementos rc de A (la matriz en el sentido usual).

Historia

El estudio de matrices es bastante antiguo. A 3-por-3 cuadrado mágico aparece en La literatura china que data ya desde 650 AC.

Matrices tienen un largo historial de aplicación en la solución de ecuaciones lineales . Un importante Texto chino de entre 300 aC y 200 dC, Los nueve capítulos en el arte matemático (Jiu Zhang Suan Shu), es el primer ejemplo de la utilización de métodos de matrices para resolver ecuaciones simultáneas . En el séptimo capítulo, "demasiado y no lo suficiente", el concepto de un determinante aparece por primera vez casi 2000 años antes de su publicación por el Matemático japonés Seki Kowa en 1683 y el matemático alemán Gottfried Leibniz en 1693.

Cuadrados mágicos eran conocidos Matemáticos árabes, posiblemente ya en el siglo séptimo, cuando los árabes conquistaron partes del noroeste de la Subcontinente indio y aprendió matemáticas de la India y astronomía, incluyendo otros aspectos de la matemática combinatoria . También se ha sugerido que la idea vino a través de China. Los primeros cuadrados mágicos de orden 5 y 6 aparecen en una enciclopedia de Bagdad alrededor 983 AD, el Enciclopedia de los Hermanos de la Pureza (Rasa'il Ihkwan al-Safa); cuadrados mágicos simples eran conocidos por varios matemáticos árabes anteriores.

Tras el desarrollo de la teoría de los determinantes de Seki Kowa y Leibniz en el siglo 17, Cramer desarrolló la teoría más en el siglo 18, la presentación de La regla de Cramer en 1750 . Carl Friedrich Gauss y Wilhelm Jordan desarrolló Gauss-Jordan eliminación en el 1800.

El término "matriz" fue acuñado en 1848 por JJ Sylvester. Cayley, Hamilton, Grassmann, Frobenius y von Neumann son algunos de los famosos matemáticos que han trabajado en la teoría de matrices.

Olga Taussky-Todd (1906-1995) hizo importantes contribuciones a la teoría de la matriz, usándolo para investigar un fenómeno aerodinámico llamado aleteo o aeroelasticidad durante la Segunda Guerra Mundial . Ha sido llamado "un portador de la antorcha" de la teoría de matrices.

Educación

Las matrices fueron enseñadas tradicionalmente como parte de álgebra lineal en la universidad, o con el cálculo. Con la adopción de integrado textos de matemáticas para su uso en la escuela secundaria en la década de 1990, han sido incluidos por muchos textos tales como el Core-Plus Proyecto de matemáticas que se dirige a menudo ya en el noveno grado, o antes, para los estudiantes de honores. A menudo requieren el uso de calculadoras gráficas como la TI-83 que puede realizar operaciones complejas tales como la inversión de matrices muy rápidamente.

Aunque la mayoría de los lenguajes de programación no están diseñados con comandos o bibliotecas de matrices, ya en la década de 1970, algunos equipos de escritorio de ingeniería, tales como la HP 9830 tenía cartuchos ROM para agregar comandos BASIC para matrices. Algunos lenguajes de programación tales como APL, fueron diseñados para manipular matrices, y los programas de matemáticas como Mathematica, junto con Arce, Matlab, y Octave también se utilizan para ayudar a la computación con matrices.

Aplicaciones

Encryption

Las matrices pueden ser utilizadas para cifrar los datos numérico. El cifrado se hace multiplicando la matriz de datos con una matriz de teclas. El descifrado se hace simplemente multiplicando la matriz cifrada con la inversa de la clave.

Gráficos de computadora

4 × 4 matrices de transformación se utilizan comúnmente en los gráficos por ordenador. La parte superior izquierda 3 × 3 de una matriz de transformación se compone de la nueva X, Y, y Z ejes de la post-transformación de coordenadas espacio.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Matrix_(mathematics)&oldid=199124713 "