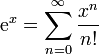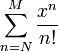N??mero Real

Temas relacionados: Matem??ticas

Antecedentes

Esta selecci??n Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Est?? disponible como una descarga intranet. Haga clic aqu?? para obtener m??s informaci??n sobre SOS Children.

En matem??ticas , los n??meros reales pueden ser descritos de manera informal como n??meros que se pueden dar por una infinita representaci??n decimal, como 2,4871773339 .... Los n??meros reales incluyen tanto los n??meros racionales , como el 42 y -23 / 129 y los n??meros irracionales , tales como π y la ra??z cuadrada de 2, y puede ser representado como puntos a lo largo de un tiempo infinitamente largo numero de linea.

Una definici??n m??s rigurosa de los n??meros reales fue uno de los acontecimientos m??s importantes del siglo 19 las matem??ticas. Definiciones populares en uso hoy en d??a incluyen clases de equivalencia de Secuencias de Cauchy de n??meros racionales, Cortes de Dedekind, una versi??n m??s sofisticada de "representaci??n decimal", y una definici??n axiom??tica de los n??meros reales como la ??nica completo Arqu??medes ordenado campo.

Los n??meros reales de nombres surgieron para distinguirlas de lo que se llam?? entonces los n??meros imaginarios (y ahora los n??meros complejos ).

Propiedades b??sicas

Un n??mero real puede ser racional o irracional ; cualquiera de los dos algebraica o trascendental; y tambi??n positivo, negativo o cero .

Bienes medida n??meros cantidades continuas. Ellos pueden, en teor??a, ser expresados por representaciones decimales que tienen una secuencia infinita de d??gitos a la derecha del punto decimal; estas son a menudo representados en la misma forma que 324,823211247 ... El elipsis (tres puntos) indican que todav??a habr??a m??s d??gitos para venir.

M??s formalmente, los n??meros reales tienen las dos propiedades b??sicas de ser un campo ordenado, y que tiene la propiedad del l??mite superior menos. La primera dice que los n??meros reales comprenden una campo, con la suma y la multiplicaci??n y divisi??n de n??meros distintos de cero, lo que puede ser totalmente ordenado en una recta num??rica de una manera compatible con la suma y la multiplicaci??n. La segunda dice que si un conjunto no vac??o de n??meros reales tiene una l??mite superior, entonces tiene una extremo superior. Estos dos juntos definen los n??meros reales por completo, y permite que sus otras propiedades a deducir. Por ejemplo, podemos probar a partir de estas propiedades que todo polinomio de grado impar con coeficientes reales tiene una ra??z real, y que si se agrega la ra??z cuadrada de -1 a los n??meros reales, la obtenci??n de los n??meros complejos , el resultado es algebraicamente cerrado.

Usos

Las mediciones en las ciencias f??sicas son casi siempre concebidos como aproximaciones a los n??meros reales. Mientras que los n??meros usados para este prop??sito son generalmente fracciones decimales que representan n??meros racionales, escrito en t??rminos decimales sugiere que son una aproximaci??n a un n??mero real subyacente te??rico.

Un n??mero real se dice que es computable si existe un algoritmo que produce sus d??gitos. Porque no s??lo son numerable de algoritmos, pero un n??mero incontable de reales, la mayor??a de los n??meros reales no son computables. Algunos constructivistas aceptan la existencia de s??lo los reales que son computables. El conjunto de n??meros definibles es m??s amplio, pero todav??a s??lo contable.

Computadoras s??lo pueden aproximar la mayor??a de los n??meros reales. M??s com??nmente, pueden representar un cierto subconjunto de los n??meros racionales con exactitud, ya sea a trav??s n??meros de punto flotante o n??meros de punto fijo, y estos n??meros racionales se utilizan como una aproximaci??n para otros valores reales cercanas. Precisi??n arbitraria es un m??todo para representar n??meros racionales arbitrarias, limitado solamente por disponibles memoria, pero m??s com??nmente se utiliza un n??mero fijo de bits de precisi??n determinados por el tama??o de la registros del procesador. Adem??s de estos valores racionales, sistemas de ??lgebra computacional son capaces de tratar muchos (contables) n??meros irracionales exactamente almacenando una descripci??n algebraica (como "(2) sqrt") en lugar de su aproximaci??n racional. Tenga en cuenta que un par de lenguajes de programaci??n utilizan "real" para describir su num??rico principal tipo de datos, tales como AppleScript.

Los matem??ticos usan el s??mbolo R (o, alternativamente, 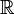$\ Bbb {R}$ , La carta " R "en pizarra negrita, Unicode ℝ) para representar el conjunto de todos los n??meros reales. La notaci??n R ⁿ se refiere a un n - espacio dimensional con coordenadas reales; por ejemplo, un valor de R ³ consta de tres n??meros reales y especifica una ubicaci??n en el espacio 3-dimensional.

En matem??ticas, los bienes se usa como adjetivo, lo que significa que el campo subyacente es el campo de los n??meros reales. Por ejemplo verdadera matriz , bienes polinomio y reales Acu??stese ??lgebra. Como sustantivo, el t??rmino se utiliza casi estrictamente en referencia a los n??meros reales, ellos mismos (por ejemplo, el "conjunto de todos los n??meros reales").

Historia

Fracciones vulgares hab??an sido utilizados por el Egipcios alrededor 1000 aC; la V??dica " Sulba Sutras "(" regla de los acordes "en s??nscrito ), ca. 600 aC, incluye lo que puede ser el primer ??utilizaci??n?? de los n??meros irracionales .

Alrededor 500 aC, los griegos matem??ticos dirigidos por Pit??goras se dio cuenta de la necesidad de los n??meros irracionales , en particular, la irracionalidad de la ra??z cuadrada de dos.

En las 18a y decimonoveno siglos hab??a mucho trabajo en irracional y n??meros trascendentes. Lambert (1761) dio la primera prueba defectuoso que π no puede ser racional, Legendre (1794) complet?? la prueba, y demostr?? que π no es la ra??z cuadrada de un n??mero racional. Ruffini (1799) y Pruebas Abel (1842), ambos construidos de Abel-Ruffini teorema: que el general ecuaciones de quinto grado o superior no pueden ser resueltos por una f??rmula general que incluye ??nicamente las operaciones aritm??ticas y ra??ces.

Evariste Galois (1832) desarroll?? t??cnicas para determinar si una ecuaci??n dada podr??a ser resuelto por los radicales que dieron lugar al campo de la teor??a de Galois . Joseph Liouville (1840) mostr?? que ni correo ni e ² pueden ser la ra??z de un n??mero entero ecuaci??n de segundo grado , y luego estableci?? la existencia de n??meros trascendentales, la prueba siendo desplazado posteriormente por Georg Cantor (1873). Charles Hermite (1873) demostr?? por primera vez que e es trascendental, y Ferdinand von Lindemann (1882), demostr?? que π es trascendental. Prueba de Lindemann se simplifica mucho por Weierstrass (1885), a??n m??s por David Hilbert (1893), y finalmente se ha hecho elemental por Hurwitz y Paul Albert Gordan.

El desarrollo del c??lculo en los a??os 1700 utiliza todo el conjunto de los n??meros reales sin haberlas definido limpiamente. La primera definici??n rigurosa fue dada por Georg Cantor en 1871 . En 1874 se demostr?? que el conjunto de todos los n??meros reales es uncountably infinita, pero el conjunto de todos n??meros algebraicos es infinito numerable. Contrariamente a la creencia generalizada, su m??todo no era su famoso argumento diagonal, que public?? en 1891.

Definici??n

Construcci??n de los n??meros racionales

Los n??meros reales pueden ser construidos como una realizaci??n de los n??meros racionales de tal manera que una secuencia definida por una decimal o binario de expansi??n como {3, 3,1, 3,14, 3,141, 3,1415, ...} converge a un ??nico n??mero real. Para obtener m??s informaci??n y otras construcciones de los n??meros reales, consulte construcci??n de los n??meros reales.

Enfoque axiom??tico

Sea R denota el conjunto de todos los n??meros reales. Entonces:

El conjunto R es una campo, lo que significa que adem??s y multiplicaci??n est??n definidas y tienen las propiedades habituales.
El campo R es orden??, lo que significa que hay una total de ≥ orden tal que, para todos los n??meros reales x, y y z:
- si x ≥ y entonces x + z ≥ y + z;
- si x ≥ 0 ey ≥ 0 entonces xy ≥ 0.
El orden es -Dedekind completa; es decir, cada no vac??o subconjunto S de R con un l??mite superior en R tiene una unido (tambi??n llamado supremo) superior menos en R.

La ??ltima propiedad es lo que diferencia a los reales de los n??meros racionales . Por ejemplo, el conjunto de los racionales con plaza de menos de 2 tiene un l??mite superior racional (por ejemplo, 1,5), pero no menos racional l??mite superior, porque la ra??z cuadrada de 2 no es racional.

Los n??meros reales se especifican ??nicamente por las propiedades anteriores. M??s precisamente, dado cualquier dos campos ordenados Dedekind-completos R ₁ y R _2, existe un campo ??nico isomorfismo de R ₁ a R _2, lo que nos permite pensar en ellos como esencialmente el mismo objeto matem??tico.

Por otra axiomatizaci??n de R, ver Axiomatizaci??n de Tarski de los reales.

Propiedades

Lo completo

La raz??n principal para la introducci??n de los reales es que los reales contienen todos los l??mites . M??s t??cnicamente, los reales son completa (en el sentido de espacios m??tricos o espacios uniformes, lo cual es una sensaci??n diferente a la integridad Dedekind de la orden en la secci??n anterior). Esto significa lo siguiente:

Una secuencia (x _n) de n??meros reales se denomina Secuencia de Cauchy si para cualquier ε> 0 existe un entero N (posiblemente dependiendo de ε) tal que la distancia | x _n - _m x | es menor que ε para todo n y m, que son ambos mayores que N. En otras palabras, una secuencia es una Sucesi??n de Cauchy si sus elementos x _n eventualmente llegan y permanecen arbitrariamente cerca uno del otro.

Una secuencia (x _n) converge al l??mite de x si para cualquier ε> 0 existe un entero N (posiblemente dependiendo de ε) tal que la distancia | x _n - x | es menor que ε siempre que n es mayor que N. En otras palabras, una secuencia tiene un l??mite de x si sus elementos eventualmente llegan y permanecen arbitrariamente cerca de x.

Es f??cil ver que cada sucesi??n convergente es una sucesi??n de Cauchy. Un hecho importante acerca de los n??meros reales es que el contrario tambi??n es cierto:

Cada secuencia de Cauchy de n??meros reales es convergente.

Es decir, los reales est??n completos.

Tenga en cuenta que los n??meros racionales no son completos. Por ejemplo, la secuencia (1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ...) es Cauchy pero no converge a un n??mero racional. (En los n??meros reales, en contraste, converge a la ra??z cuadrada de 2.)

La existencia de l??mites de sucesiones de Cauchy es lo que hace el c??lculo de trabajo y es de gran utilidad pr??ctica. La prueba num??rica est??ndar para determinar si una secuencia tiene un l??mite es para probar si es una secuencia de Cauchy, como el l??mite normalmente no se conoce de antemano.

Por ejemplo, la serie est??ndar de la funci??n exponencial

$\ Mathrm {e} ^ x = \ sum_ {n = 0} ^ {\ infty} \ frac {x ^ n} {n!}$

converge a un n??mero real porque por cada x las sumas

$\ Sum_ {n = N} ^ {M} \ frac {x ^ n} {n!}$

se puede hacer arbitrariamente peque??o eligiendo N suficientemente grande. Esto demuestra que la secuencia es de Cauchy, as?? que sabemos que la sucesi??n converge incluso si el l??mite no se conoce de antemano.

"El campo completo ordenado"

Los n??meros reales son a menudo descrito como "el campo pedido completo", una frase que se puede interpretar de varias maneras.

En primer lugar, una orden puede ser -ret??culo completo. Es f??cil ver que hay un campo ordenado puede ser enrejado completo, ya que puede tener ning??n elemento m??s grande (dada cualquier elemento z, z + 1 es m??s grande), por lo que este no es el sentido que se quiere decir.

Adem??s, una orden puede ser Dedekind-completa, tal como se define en la secci??n de axiomas. El resultado de unicidad al final de esa secci??n justifica usando la palabra "el" "campo completo ordenado" en la frase cuando este es el sentido de "completo" que se quiere decir. Este sentido de integridad est?? m??s estrechamente relacionado con la construcci??n de los reales de los cortes de Dedekind, ya que la construcci??n se inicia a partir de un campo ordenado (los racionales) y luego forma la Dedekind-realizaci??n de la misma en una forma est??ndar.

Estas dos nociones de integridad ignoran la estructura exterior. Sin embargo, una grupo ordenado (en este caso, el grupo aditivo del campo) define una estructura uniforme y estructuras uniformes tienen una noci??n de integridad (topolog??a); la descripci??n en la secci??n de Integridad de arriba es un caso especial. (Nos referimos a la noci??n de integridad en espacios uniformes en lugar de la noci??n relacionada y m??s conocido por espacios m??tricos, ya que la definici??n de espacio m??trico se basa en que ya tiene una caracterizaci??n de los n??meros reales.) No es cierto que R es el campo ordenado s??lo se completa de manera uniforme, pero es la ??nica completa uniformemente Campo de Arqu??medes, y de hecho a menudo se oye la frase "campo de Arqu??medes completa" en vez de "completo campo orden??". Dado que puede ser probado que cualquier campo de Arqu??medes completa uniformemente tambi??n debe ser Dedekind-completa (y viceversa, por supuesto), lo que justifica el uso de "la" en la frase "el campo de Arqu??medes completa". Este sentido de integridad est?? m??s estrechamente relacionado con la construcci??n de los reales de secuencias de Cauchy (la construcci??n lleva a cabo en su totalidad en este art??culo), ya que comienza con un campo de Arqu??medes (los racionales) y forma la terminaci??n uniforme de la misma en un est??ndar manera.

Pero el uso original de la frase "campo de Arqu??medes completa" era por David Hilbert , que significaba todav??a algo m??s por ella. ??l quiso decir que los n??meros reales forman el campo de Arqu??medes m??s grande en el sentido de que todos los dem??s campos de Arqu??medes es un subcampo de la R. As?? R est?? "completo" en el sentido de que nada m??s se puede a??adir a ella sin que sea ya no es un campo de Arqu??medes. Este sentido de integridad est?? m??s estrechamente relacionado con la construcci??n de los reales de n??meros surrealistas, ya que la construcci??n comienza con una clase adecuada que contiene todos los campos ordenado (los surreals) y luego selecciona del mismo el mayor subcampo de Arqu??medes.

Propiedades avanzadas

Los reales son incontable; es decir, no son estrictamente m??s n??meros reales que los n??meros naturales , a pesar de que ambos conjuntos son infinitos . De hecho, la cardinalidad de los reales es igual a la del conjunto de subconjuntos de los n??meros naturales, y Argumento diagonal de Cantor afirma que la cardinalidad de este ??ltimo conjunto es estrictamente mayor que la cardinalidad de N. Dado que s??lo un conjunto numerable de n??meros reales puede ser algebraica, casi todos los n??meros reales son trascendental. La no existencia de un subconjunto de los reales con cardinalidad estrictamente entre el de los enteros y los reales se conoce como el hip??tesis del continuo. La hip??tesis del continuo puede ser probada ni ser refutada; es independiente de los axiomas de la teor??a de conjuntos .

Los n??meros reales forman una espacio m??trico: la distancia entre X e Y se define como el valor absoluto | x - y |. En virtud de ser una totalmente ordenado conjunto, sino que tambi??n llevan un ordenar topolog??a; la topolog??a derivada de la m??trica y la derivada de la orden son id??nticos. Los reales son un contr??ctil (de ah?? conectado y simplemente conexo), espacio m??trico separable de dimensi??n 1, y se denso en todas partes. Los n??meros reales son localmente compacto pero no compacta . Hay varias propiedades que especifican ellos ??nicamente; por ejemplo, todos sin l??mites, conectado, y separable topolog??as orden son necesariamente homeomorfo a los reales.

Cada n??mero real no negativo tiene una ra??z cuadrada en R, y ning??n n??mero negativo hace. Esto demuestra que el orden en R est?? determinada por su estructura algebraica. Adem??s, todo polinomio de grado impar admite al menos una ra??z: estas dos propiedades hacen R la principal ejemplo de un campo real cerrado. Demostrando este es el primer medio de una prueba de la teorema fundamental del ??lgebra.

Los reales llevan una can??nica medir, la Lebesgue medida, que es la Medida de Haar en su estructura como una grupo topol??gico normaliz?? tal que la intervalo unidad [0,1] tiene la medida 1.

El axioma del supremo de los reales se refiere a subconjuntos de los n??meros reales y por lo tanto es una afirmaci??n l??gica de segundo orden. No es posible caracterizar los reales con l??gica de primer orden solo: la L??wenheim-Skolem teorema implica que existe un subconjunto denso numerable de los n??meros reales que satisfacen exactamente las mismas frases en l??gica de primer orden como los propios n??meros reales. El conjunto de n??meros hiperreales cumple las mismas primeras frases de orden como R. Campos ordenados que satisfagan las mismas frases de primer orden como el R se llaman modelos no est??ndar de R. Esto es lo que hace trabajo de an??lisis no est??ndar; demostrando una declaraci??n de primer orden en alg??n modelo no est??ndar (que puede ser m??s f??cil de lo que demuestra que en I), sabemos que la misma declaraci??n tambi??n debe ser verdad de R.

Las generalizaciones y extensiones

Los n??meros reales pueden generalizarse y extenderse en varias direcciones diferentes:

Los n??meros complejos contienen soluciones a todos los polinomios ecuaciones y por lo tanto son una algebraicamente campo cerrado a diferencia de los n??meros reales. Sin embargo, los n??meros complejos no son una campo ordenado.
La sistema de n??meros reales affinely extendida a??ade dos elementos + ∞ y -∞. Es un espacio compacto . Ya no es un campo, ni siquiera un grupo aditivo; todav??a tiene una total de la orden; Por otra parte, es una enrejado completo.
La l??nea descriptivo verdadero agrega s??lo un valor ∞. Tambi??n es un espacio compacto. Una vez m??s, ya no es un campo, ni siquiera un grupo aditivo. Sin embargo, se permite la divisi??n de un elemento distinto de cero por cero. No se orden?? m??s.
La l??nea real a largo pega juntos ℵ ₁ * + ℵ ₁ copias de la recta real m??s un solo punto (en este caso ℵ ₁ * denota el orden invertido de ℵ ₁₎ para crear un conjunto ordenado que es "localmente" id??nticos a los n??meros reales, pero de alguna manera m??s largo; por ejemplo, hay una incrustaci??n orden conservaci??n de ℵ ₁ en la l??nea real de largo pero no en los n??meros reales. La l??nea real de largo es el mayor conjunto ordenado que es Arqu??medes completa y localmente. Al igual que con los dos ejemplos anteriores, este conjunto ya no es un campo o grupo aditivo.
Campos ordenados extienden los reales son la n??meros hiperreales y la n??meros surrealistas; ambos contener n??meros infinitesimales e infinitamente grandes y por lo tanto no son Arqu??medes.
Operadores autoadjunto en un Espacio de Hilbert (por ejemplo, complejos cuadrados autoadjuntos matrices ) generalizar los reales en muchos aspectos: se pueden solicitar (aunque no totalmente ordenado), que est??n completos, todos sus valores propios son reales y forman un verdadero ??lgebra asociativa. Operadores definidas positivas corresponden a los reales positivos y operadores normales corresponden a los n??meros complejos.

"reales" en la teor??a de conjuntos

En la teor??a de conjuntos , en concreto la teor??a de conjuntos descriptiva del Espacio de Baire se utiliza como un sustituto para los n??meros reales ya que este ??ltimo tiene algunas propiedades topol??gicas (connectedness) que son un inconveniente t??cnico. Elementos de espacio de Baire se conocen como "reales".

Recuperado de " http://en.wikipedia.org/w/index.php?title=Real_number&oldid=198231227 "