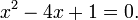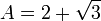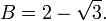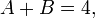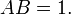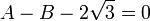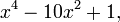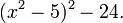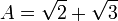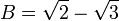La teoría de Galois

Evariste Galois (1811-1832)

En matemáticas , más específicamente en el álgebra abstracta , la teoría de Galois, nombrado después Evariste Galois, proporciona una conexión entre la teoría del campo y la teoría de grupos . Usando la teoría de Galois, ciertos problemas en la teoría del campo se pueden reducir a la teoría de grupos, que en cierto sentido es más simple y mejor comprendido.

Originalmente Galois utilizado grupos de permutaciones para describir cómo los distintos raíces de un determinado polinomio de la ecuación están relacionados entre sí. El enfoque moderno de la teoría de Galois, desarrollado por Richard Dedekind, Leopold Kronecker y Emil Artin, entre otros, implica estudiar automorfismos extensiones de campo.

Además abstracción de la teoría de Galois se logra mediante la teoría de la Conexiones de Galois.

Aplicación a los problemas clásicos

El nacimiento de la teoría de Galois fue motivada originalmente por la siguiente pregunta, cuya respuesta se conoce como el Teorema de Abel-Ruffini.

"¿Por qué hay ninguna fórmula para las raíces de una quinta parte (o superior) grado ecuación polinómica en términos de los coeficientes del polinomio, utilizando únicamente las operaciones usuales algebraicas (suma, resta, multiplicación, división) y la aplicación de los radicales (raíces cuadradas , raíces cúbicas, etc.)? "

La teoría de Galois no sólo proporciona una hermosa respuesta a esta pregunta, sino que también explica en detalle por qué es posible resolver ecuaciones de grado de cuatro o más bajo de la manera anterior, y por qué sus soluciones toman la forma que lo hacen. Además, se proporciona un medio conceptualmente claras, ya menudo prácticos, de narración cuando alguna ecuación particular de grado superior se puede resolver de esa manera.

La teoría de Galois también da una idea clara de las cuestiones relativas a problemas en compás y una regla de construcción. Se da un elegante caracterización de las proporciones de longitudes que pueden ser construidos con este método. El uso de este, se hace relativamente fácil responder a este tipo de problemas clásicos de la geometría como

"regulares Qué polígonos son polígonos construibles? "

"Por qué no es posible trisecar cada ángulo? "

Historia

La teoría de Galois se originó en el estudio de funciones simétricas - los coeficientes de un polinomio son (para firmar) el polinomios simétricos elementales en las raíces. Por ejemplo, (x - a) (x - b) = x ² - (a + b) x + ab, donde 1, a + b y AB son los polinomios elementales de grado 0, 1 y 2 en dos variables.

Esto se formalizó por primera vez por el matemático francés del siglo 16 François Viète, en Fórmulas de Viète, para el caso de raíces reales positivas. En la opinión del matemático británico del siglo 18 Charles Hutton, la expresión de los coeficientes de un polinomio en términos de las raíces (no sólo para las raíces positivas) se entendió por primera vez por el matemático francés del siglo 17 Albert Girard; Hutton escribe:

... [Girard fue] la primera persona que entiende la doctrina general de la formación de los coeficientes de las potencias de la suma de las raíces y sus productos. Él fue el primero que descubrió las reglas para sumar las potencias de las raíces de cualquier ecuación.

En este orden de ideas, la discriminante es una función simétrica en las raíces que refleja las propiedades de las raíces - es cero si y sólo si el polinomio tiene una raíz múltiple, y para los polinomios cuadráticos y cúbicos es positivo si y sólo si todas las raíces son reales y distintas, y negativo si y sólo si hay un par de raíces complejas conjugadas distintas. Ver Discriminante: naturaleza de las raíces para obtener más detalles.

La primera parte fue cúbico resuelto por el 15 / matemático italiano del siglo 16 Scipione del Ferro, quien no obstante publicar sus resultados; este método sólo resuelve una de las tres clases, como los otros involucrados tomando raíces cuadradas de números negativos, y los números complejos no se conocían en el momento. Esta solución se redescubrió independientemente en 1535 por Niccolò Fontana Tartaglia, quien compartió con Gerolamo Cardano, pidiéndole que lo publicó. Cardano luego se extendió esto a los otros dos casos, el uso de raíces cuadradas de los negativos como pasos intermedios; ver los detalles en Método de Cardano. Tras el descubrimiento de la obra de Ferro, sintió que el método de Tartaglia ya no era secreto, y por lo tanto él publicó su solución completa en su 1545 Ars Magna. Su alumno Lodovico Ferrari resolvió el polinomio de cuarto grado, que la solución Cardano también incluido en Ars Magna.

Un paso más allá fue el 1770 de papel Réflexions sur la résolution algébrique des ecuaciones por el matemático francés-italiano Joseph Louis Lagrange , en su método de Resolventes Lagrange, donde analizó solución Cardano y de Ferrarri de las cúbicas y cuárticas considerándolos en términos de permutaciones de las raíces, que arrojó un polinomio auxiliar de grado inferior, proporcionando una comprensión unificada de las soluciones y sentar las bases de la teoría de grupos y Galois teoría. Fundamentalmente, sin embargo, que no consideraba composición de permutaciones. Método de Lagrange no se extendió a las ecuaciones de quinto grado o superior, debido a que el resolutivo tenía mayor grado.

La ecuación de quinto grado fue casi demostrado no tener soluciones generales de los radicales por Paolo Ruffini en 1799 , cuya idea clave era utilizar grupos de permutaciones, y no sólo una única permutación. Su solución contenía una brecha, que Cauchy considerado menor de edad, aunque esto no fue parcheado hasta que el trabajo del matemático noruego Niels Henrik Abel, que publicó una demostración en 1824, estableciendo así el Teorema de Abel-Ruffini.

Mientras Ruffini y Abel establecieron que la de quinto grado no se podía resolver, algunos quínticas particulares pueden ser resueltos, tales como (x - 1) ^5, y el criterio exacto por el cual un polinomio de quinto grado o superior dado se pudo determinar que ser solucionable o no fue dada por Evariste Galois, que mostró que si un polinomio era solucionable o no era equivalente a si el grupo de la permutación de sus raíces - en términos modernos, su Grupo de Galois - tenía una cierta estructura - en términos modernos, si era o no una grupo resoluble. Este grupo fue siempre solucionables para polinomios de grado de cuatro o menos, pero no siempre es así que para polinomios de grado cinco y mayor, lo que explica por qué no hay solución general en mayor grado.

El enfoque de grupo de la permutación de la teoría de Galois

Dado un polinomio, puede ser que algunas de las raíces están conectados por diversos ecuaciones algebraicas. Por ejemplo, puede ser que para dos de las raíces, dicen A y B, que A ² + 5 = 7 B ^3. La idea central de la teoría de Galois es considerar las permutaciones (o reordenamientos) de las raíces que tiene la propiedad de que cualquier ecuación algebraica satisfecho por las raíces es todavía satisfecho después de las raíces se han permutado. Una condición importante es que nos limitamos a ecuaciones algebraicas cuyos coeficientes son números racionales . (Se podría especificar un determinado lugar campo en el que los coeficientes mienta, pero, para los ejemplos simples abajo, nos limitaremos al campo de los números racionales.)

Estas permutaciones juntos forman un grupo de la permutación, también llamado el Grupo de Galois del polinomio (en los números racionales). Para ilustrar este punto, considere los siguientes ejemplos:

Primer ejemplo - una ecuación cuadrática

Considere la ecuación de segundo grado

Mediante el uso de la fórmula cuadrática , encontramos que las dos raíces están

Ejemplos de ecuaciones algebraicas satisfechos por A y B incluyen

y

Obviamente, en cualquiera de estas ecuaciones, si intercambiamos A y B, obtenemos otra declaración verdadera. Por ejemplo, la ecuación A + B = 4 se convierte simplemente en B + A = 4. Por otra parte, es cierto, pero mucho menos obvio, que este se mantiene para cada posible ecuación algebraica con racional coeficientes satisfechos por la raíz A y B; para probar esto requiere la teoría de la polinomios simétricos.

Llegamos a la conclusión de que el grupo de Galois del polinomio x ² - 4 x + 1 se compone de dos permutaciones: la identidad de permutación que deja A y B sin tocar, y el permutación transposición que intercambia A y B. Es un grupo cíclico de orden dos, y por lo tanto isomorfo a Z / Z 2.

Se podría objetar que A y B están relacionadas por otra ecuación algebraica,

que no permanece cierto cuando A y B se intercambian. Sin embargo, esta ecuación no nos concierne, porque no tiene coeficientes racionales; en particular, 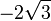es no racional.

Una discusión similar se aplica a cualquier polinomio cuadrático ax ² + bx + c, donde a, b y c son números racionales.

• Si el polinomio tiene sólo una raíz, por ejemplo x ² - 4 x + 4 = (x -2) ^2, entonces el grupo de Galois es trivial; es decir, que sólo contiene la permutación identidad.
• Si tiene dos raíces racionales distintas, por ejemplo x ² - 3 x + 2 = (x -2) (x-1), el grupo de Galois es de nuevo trivial.
• Si tiene dos raíces irracionales (incluyendo el caso en que las raíces son complejas ), entonces el grupo de Galois contiene dos permutaciones, al igual que en el ejemplo anterior.

Segundo ejemplo

Considere el polinomio

que también puede ser escrito como

Deseamos para describir el grupo de Galois de este polinomio, de nuevo sobre el campo de los números racionales . El polinomio tiene cuatro raíces:

Hay 24 formas posibles para permutar estas cuatro raíces, pero no todas estas permutaciones son miembros del grupo de Galois. Los miembros del grupo de Galois deben preservar cualquier ecuación algebraica con coeficientes racionales que involucran A, B, C y D. Uno de tales ecuación es

A + D = 0.

Sin embargo, desde

,

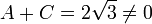la permutación

(A, B, C, D) → (A, B, D, C)

no está permitido (porque transforma la ecuación válida A + D = 0 en la ecuación no válido A + C = 0).

Otra ecuación que satisfacen las raíces es

Esto excluirá otras permutaciones, como

(A, B, C, D) → (A, C, B, D).

Continuando de esta manera, nos encontramos con que las únicas permutaciones (que satisfacen ambas ecuaciones simultáneamente) restante son

(A, B, C, D) → (A, B, C, D)

(A, B, C, D) → (C, D, A, B)

(A, B, C, D) → (B, A, D, C)

(A, B, C, D) → (D, C, B, A),

y el grupo de Galois es isomorfo al Grupo de Klein.

El enfoque moderno de la teoría del campo

En el enfoque moderno, se empieza con una campo de extensión L / K (léase: L sobre K), y examina el grupo de campo automorfismos de L / K (estos son asignaciones α: L → L con α (x) = x para todo x en K). Ver el artículo sobre Grupos de Galois para más explicaciones y ejemplos.

La conexión entre los dos enfoques es la siguiente. Los coeficientes del polinomio en cuestión deben ser elegidos desde el campo base de K. El campo superior L debe ser el campo obtenido por contiguo a las raíces del polinomio en cuestión para el campo base. Cualquier permutación de las raíces que respete ecuaciones algebraicas como se describe anteriormente da lugar a un automorfismo de L / K, y viceversa.

En el primer ejemplo anterior, estábamos estudiando la extensión Q (√3) / Q, donde Q es el campo de los números racionales , y Q (√3) es el campo obtenida de Q por √3 contiguo. En el segundo ejemplo, estábamos estudiando la extensión Q (A, B, C, D) / Q.

Hay varias ventajas para el enfoque moderno sobre el enfoque de grupo de la permutación.

• Permite una declaración mucho más simple de la teorema fundamental de la teoría de Galois.
• El uso de campos de bases distintas de Q es crucial en muchas áreas de las matemáticas. Por ejemplo, en teoría algebraica de números, a menudo se hace uso de la teoría de Galois campos de número, campos finitos o campos locales como el campo base.
• Se permite estudiar con mayor facilidad las extensiones infinitas. De nuevo, esto es importante en la teoría algebraica de números, donde, por ejemplo, a menudo se discute la grupo absoluto de Galois de Q, definido para ser el grupo de Galois de K / Q donde K es una clausura algebraica de Q.
• Permite a la consideración de extensiones inseparables. Este problema no se plantea en el marco clásico, ya que siempre se asume implícitamente que la aritmética se llevó a cabo en característica cero, pero no cero característica surge con frecuencia en la teoría de números y en geometría algebraica.
• Se elimina la dependencia bastante artificial en perseguir raíces de polinomios. Es decir, diferentes polinomios pueden producir los mismos campos de extensión, y el enfoque moderno reconoce la conexión entre estos polinomios.

Grupos resolubles y solución por radicales

La noción de una grupo resoluble en la teoría de grupos permite determinar si un polinomio tiene solución en los radicales, en función de si su grupo de Galois tiene la propiedad de solvencia. En esencia, cada campo de extensión L / K corresponde a una grupo de factor en una serie de composición del grupo de Galois. Si un grupo factor en la serie de composición es cíclico de orden n, entonces si el campo correspondiente extensión es una extensión de un campo que contiene una raíz primitiva de la unidad, entonces es una extensión radical, y los elementos de L entonces se puede expresar mediante la raíz enésima de algún elemento de K.

Si todos los grupos factor en su serie de composición son cíclicos, el grupo de Galois se llama solución, y todos los elementos del campo correspondiente se puede encontrar mediante la adopción de repetidamente raíces, productos y sumas de elementos desde el campo base (por lo general Q) .

Uno de los grandes triunfos de la Teoría de Galois fue la prueba de que para cada n> 4, existen polinomios de grado n que no son resolubles por radicales-la Teorema de Abel-Ruffini. Esto es debido al hecho de que para n> 4 la simétrica grupo S _n contiene una simple, no cíclico, subgrupo normal.

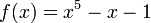El polinomio . La verdadera raíz solitario 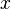= 1,1673 ... es algebraico, pero no expresable como radicales. Los otros cuatro raíces son números complejos .

Un ejemplo de quinto grado no solucionable

Van der Waerden cita el polinomio 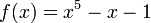. Por el teorema de la raíz racional no tiene ceros racionales. Tampoco tiene factores lineales módulo 2 o 3.

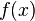tiene la factorización 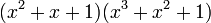modulo 2. Eso significa que su grupo de Galois módulo 2 es cíclico de orden 6.

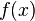tiene ningún factor de módulo cuadrática 3. Así pues, su grupo de Galois módulo 3 tiene orden 5.

Sabemos que un grupo de Galois módulo un primo es isomorfo a un subgrupo del grupo de Galois sobre los números racionales. Un grupo de la permutación en 5 objetos con las operaciones de las órdenes de 6 y 5 debe ser el grupo simétrico 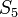, Que debe ser el grupo de Galois de 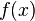. Este es uno de los ejemplos más simples de un polinomio de quinto grado no resoluble. Serge Lang dijo que Artin era aficionado a este ejemplo.

El problema inverso de Galois

Todos los grupos finitos se producen como grupos de Galois. Es fácil de construir extensiones de campo con cualquier grupo finito dado como grupo de Galois, siempre y cuando uno no también especifican el campo de tierra.

Por eso, elegir un campo K y un grupo finito G. El teorema de Cayley dice que G es (hasta isomorfismo) un subgrupo de la grupo S simétrica en los elementos de G. Elija indeterminados {x} _α, uno para cada elemento α de G, y lindan ellos a K para obtener el campo F = K ({x} _α). Contenido dentro de F es el campo de L simétrica funciones racionales en el {x} _α. El grupo de Galois de F / L es S, por un resultado básico de Emil Artin. G actúa sobre F por la restricción de la acción de S. Si el campo fijo de esta acción es H, entonces, por la teorema fundamental de la teoría de Galois, el grupo de Galois de F / M es G.

Es un problema abierto para demostrar la existencia de una extensión de campo del campo racional Q con un grupo finito dado como grupo de Galois. Hilbert tuvo un papel en la solución del problema para todos los grupos simétricos y alternantes. Igor Shafarevich demostró que todo grupo finito solucionable es el grupo de Galois de alguna extensión de Q. Varias personas han resuelto el problema inverso de Galois para no abeliano seleccionado grupos simples. Existencia de soluciones se ha demostrado para todos, pero posiblemente uno ( Grupo Mathieu M ₂₃₎ de los 26 grupos simples esporádicos. Hay incluso un polinomio con coeficientes enteros cuyo grupo de Galois es el Grupo Monstruo.