Grupo cíclico

En la teoría de grupos , un grupo cíclico o grupo monogenous es un grupo que puede ser generada por un solo elemento, en el sentido de que el grupo tiene un elemento g (llamado un " generador "del grupo) de modo que, cuando se escribe multiplicativa, cada elemento del grupo es una potencia de g (un múltiplo de g cuando la notación es aditivo).

Definición

Un grupo G se llama cíclico si existe un elemento g en G tal que G = <g> = {g ⁿ | n es un número entero}. Dado que cualquier grupo generado por un elemento en un grupo es un subgrupo de ese grupo, demostrando que la única subgrupo de un grupo G que contiene g es en sí G basta para demostrar que G es cíclico.

Por ejemplo, si G = ^{0 g, ¹ g, ² g, ³ g, ⁴ g, g ^5} es un grupo, entonces g = ⁶ g ^0, y G es cíclico. De hecho, G es esencialmente la misma que (es decir, isomorfo a) el conjunto {0, 1, 2, 3, 4, 5} con la adición de módulo 6. Por ejemplo, 1 + 2 = 3 (mod 6) corresponde a ¹ g · g = ² g ³ y 2 + 5 = 1 (mod 6) corresponde a ² g · g = ⁵ g ⁷ g = ^1, y así sucesivamente . Uno puede utilizar el isomorfismo φ φ definida por (g ⁱ⁾ = i.

Para cada entero positivo n hay exactamente un grupo cíclico (hasta isomorfismo) cuyo orden es n, y hay exactamente un grupo cíclico infinito (los números enteros bajo la adición). Por lo tanto, los grupos cíclicos son los grupos más simples y están completamente clasifican.

El nombre 'cíclico' puede ser engañoso: es posible generar un número infinito de elementos y no formar ningún ciclo literales; es decir, cada 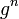es distinta. (Se puede decir que tiene un ciclo infinitamente largo.) Un grupo generado de esta manera se llama un grupo cíclico infinito, y es isomorfo al grupo aditivo de los enteros Z.

Puesto que los grupos cíclicos son abeliano, a menudo se escriben de forma aditiva y denotan Z _n. Sin embargo, esta notación puede ser problemático para los teóricos de números porque entra en conflicto con la notación habitual para p número -adic anillos o localización en una ideal primo. La cociente notaciones Z / n Z, Z / n, y Z / (n) son alternativas estándar. Adoptamos la primera de ellas para evitar la colisión de notación. Ver también la sección Subgrupos y notación abajo.

Uno puede escribir el grupo multiplicativa, y denotan por C _n, donde n es el orden (que puede ser ∞). Por ejemplo, g ³ g ⁴ g = ² en do _5, mientras que 3 + 4 = 2 en Z / 5 Z.

Propiedades

La teorema fundamental de grupos cíclicos establece que si G es un grupo cíclico de orden n entonces cada subgrupo de G es cíclico. Además, el orden de cualquier subgrupo de G es un divisor de n y k para cada divisor positivo de n el grupo G tiene exactamente un subgrupo de orden k. Esta propiedad caracteriza a grupos cíclicos finitos: un grupo de orden n es cíclico si y sólo si para cada divisor d de n el grupo tiene a lo sumo un subgrupo de orden d. A veces, la declaración equivalente se utiliza: un grupo de orden n es cíclico si y sólo si para cada divisor d de n el grupo tiene exactamente un subgrupo de orden d.

Cada grupo cíclico finito es isomorfo al grupo {[0], [1], ..., [n - 1]} de los enteros módulo n bajo la adición, y cualquier grupo cíclico infinito es isomorfo a Z (el conjunto de todos los enteros) bajo la adición. Por lo tanto, uno sólo tiene que mirar a esos grupos para comprender las propiedades de los grupos cíclicos en general. Por lo tanto, los grupos cíclicos son uno de los grupos más simples para estudiar y una serie de propiedades agradables son conocidos.

Dado un grupo cíclico G de orden n (n puede ser infinito) y por cada g en G,

• G es abeliano; es decir, su operación de grupo es conmutativo: gh = hg (para todos h en G). Esto es así ya que g + h mod n = h + g mod n.
• Si n es finito, entonces g ⁿ = g ⁰ es el elemento identidad del grupo, ya que n mod n = 0.
• Si n = ∞, entonces hay exactamente dos generadores: a saber, 1 y -1 para Z, y cualquier otro asignadas a ellos bajo un isomorfismo en otros grupos cíclicos infinitos.
• Si n es finito, entonces hay exactamente (n) generadores φ, donde φ es el Función phi de Euler
• Cada subgrupo de G es cíclico. De hecho, cada subgrupo finito de G es un grupo de {0, 1, 2, 3, ... m - 1} con modulo Además m. Y cada subgrupo infinito de G es m Z para algunos m, que es biyectiva a (de modo isomorfo a) Z.
• G _n es isomorfo a Z / n Z ( de grupo de factor de Z sobre n Z) desde Z / n Z = {0 + n Z, Z 1 + n, n + 2 Z, 3 + n Z, 4 + n Z, ..., n - 1 + n Z } 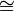{0, 1, 2, 3, 4, ..., n - 1} bajo módulo Además n.

Más generalmente, si d es un divisor de n, entonces el número de elementos en Z / n que tienen el fin d es φ (d). El orden de la clase de residuos de m es n / mcd (n, m).

Si p es un número primo , entonces el único grupo ( hasta isomorfismo) con p elementos es el grupo cíclico C o Z _p / p Z.

La producto directo de dos grupos cíclicos Z / n Z y Z / m Z es cíclico si y sólo si n y m son primos entre sí. Así, por ejemplo, Z / Z 12 es el producto directo de Z / Z 3 y Z / Z 4, pero no el producto directo de Z / 6 Z y Z / Z 2.

La definición de inmediato implica que los grupos cíclicos tienen muy simple presentación del grupo C _∞ = <x |> y C _n = <x | x ^n> para finita n.

La grupo cíclico primaria es un grupo de la forma Z / p ^k donde p es un número primo . La teorema fundamental de los grupos abelianos establece que cada grupo abeliano finitamente generado es el producto directo de un número finito de grupos cíclicos e infinitas primarias finitos cíclicos.

Z / n Z y Z también son anillos conmutativos . Si p es un primo, entonces Z / p Z es una campo finito, también denotado por F _p o GF (p). Cada campo con p elementos es isomorfo a éste.

La unidades del anillo Z / n Z son los números coprimeros a n. Ellos forman una grupo bajo la multiplicación modulo n con φ (n) elementos (véase más arriba). Está escrito como (Z / n Z) ^x. Por ejemplo, obtenemos (Z / n Z) ^x = {1,5} cuando n = 6, y obtener (Z / n Z) ^x = {1,3,5,7} cuando n = 8.

De hecho, se sabe que (Z / n Z) ^× es cíclico si y sólo si n es 2 o 4 o p ^k o 2 p ^k para una extraño número primo p y k ≥ 1, en cuyo caso cada generador de (Z / n Z) ^× se llama primitiva módulo raíz n. Por lo tanto, (Z / n Z) ^× es cíclico para n = 6, pero no para n = 8, donde es isomorfa a la vez Grupo de Klein.

El grupo (Z / p Z) ^× es cíclico con p - 1 elementos para cada primo p, y también se escribe (Z / Z p) ^*, ya que se compone de los elementos distintos de cero. Más generalmente, cada finito subgrupo del grupo multiplicativo de cualquier campo es cíclico.

Ejemplos

En 2D y 3D el grupo de simetría para n -fold simetría rotacional es C _n, del grupo del extracto del tipo Z _n. En 3D también hay otros grupos de simetría que son algebraicamente la misma, ver Grupos de simetría cíclica en 3D.

Tenga en cuenta que el grupo S ¹ de todas las rotaciones de un círculo (la grupo círculo) no es cíclico, ya que no es ni siquiera contable.

El ^enésimo raíces de la unidad forman un grupo cíclico de orden n bajo la multiplicación. por ejemplo, 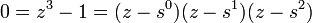donde 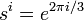y un grupo de 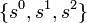bajo la multiplicación es cíclico.

La Grupo de Galois de cada finito extensión de campo de una campo finito es finito y cíclica; Por el contrario, dado un campo finito F y un grupo cíclico finito G, hay una extensión de campo finito F cuyo grupo de Galois es G.

Representación

La gráficos ciclo de grupos cíclicos finitos son todos los polígonos n -sided con los elementos en los vértices. El vértice oscuro en los gráficos de ciclo por debajo de soporte para el elemento de identidad, y los otros vértices son los otros elementos del grupo. Un ciclo consiste en sucesivas potencias de cualquiera de los elementos conectados al elemento de identidad.

C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8

La teoría de la representación del grupo cíclico es un caso base fundamental para la teoría de la representación de los grupos finitos más generales. En el complejo caso, una representación de un grupo cíclico se descompone en una suma directa de caracteres lineales, por lo que la conexión entre la teoría carácter y teoría de la representación transparente. En el caso característica positiva, las representaciones indescomponibles del grupo cíclico formar un modelo y base inductiva para la teoría de la representación de los grupos con cíclico Subgrupos de Sylow y más en general la teoría de la representación de bloques de defecto cíclico.

Subgrupos y notación

Todos subgrupos y grupos cocientes de grupos cíclicos son cíclicos. Específicamente, todos los subgrupos de Z son de la forma Z m, con m un número entero ≥0. Todos estos subgrupos son diferentes, y aparte del grupo trivial (para m = 0) todos son isomorfo a Z. La celosía de subgrupos de Z es isomorfo al dual de la red de los números naturales ordenados por divisibilidad . Todos los grupos de factores de Z son finitos, a excepción de la excepción trivial Z / {0} = Z / Z 0. Por cada divisor d positiva de n, el grupo cociente Z / n Z tiene precisamente un subgrupo de orden d, la generada por la clase de residuo n / d. No hay otros subgrupos. El entramado de subgrupos es así isomorfo al conjunto de divisores de n, ordenados por divisibilidad. En particular, es un grupo cíclico simple si y sólo si su orden (el número de sus elementos) es primo.

Utilizando el formalismo grupo cociente, Z / n Z es una notación estándar para el grupo cíclico aditivo con n elementos. En terminología anillo, el subgrupo n Z es también el ideales (n), por lo que el cociente también se puede escribir Z / (n) o Z / n sin abuso de notación. Estas alternativas no entra en conflicto con la notación para los p enteros -adic. La última forma tiene la ventaja adicional de que se lee de la misma manera que el grupo o anillo se describe a menudo verbalmente, "Zee mod en".

Como un problema práctico, uno se puede dar un subgrupo finito C de orden n, generada por un elemento g, y pidió para encontrar el tamaño m del subgrupo generado por g ^k para algún entero k. Aquí m será el menor entero> 0 tal que mk es divisible por n. Por tanto, es n / m, donde m = (k, n) es el mcd de k y n. Dicho de otra manera, la índice del subgrupo generado por g ^k es m. Este razonamiento se conoce como el Índice algoritmo de cálculo, en la teoría de números .

Endomorfismos

La anillo endomorfismo del abeliano grupo Z / n Z es isomorfo a Z / n en sí Z como anillo. Bajo este isomorfismo, el número r corresponde a la endomorphism de Z / n Z que mapea cada elemento a la suma de r copias de la misma. Esta es una biyección si y sólo si r es primos entre sí con n, por lo que la grupo de automorfismos de Z / n Z es isomorfo al grupo de unidades (Z / n Z) ^x (véase más arriba).

Del mismo modo, el anillo endomorfismo del grupo aditivo Z es isomorfo al anillo Z. Su grupo de automorfismos es isomorfo al grupo de unidades del anillo Z, es decir, a {-1, 1} 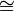C _2.

Prácticamente grupos cíclicos

Un grupo se llama virtualmente cíclico si contiene un subgrupo cíclico de finito índice. Se sabe que un finitamente generado grupo discreto con exactamente dos extremos es prácticamente cíclico. Cada subgrupo abeliano de un Grupo hiperbólico Gromov es prácticamente cíclico.