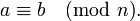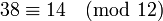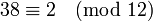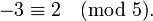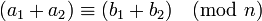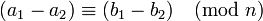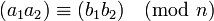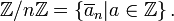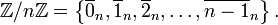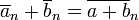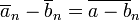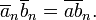La aritmética modular

Temas relacionados: Matemáticas

Acerca de este escuelas selección Wikipedia

Este contenido de Wikipedia ha sido seleccionada por SOS para su utilización en las escuelas de todo el mundo. SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?

La aritmética modular (a veces llamado módulo aritmético, o aritmética del reloj) es un sistema de aritmética de números enteros , donde el número de "envolvente" después de que alcancen un determinado valor - el módulo. La aritmética modular fue introducido por Carl Friedrich Gauss en su libro Disquisitiones Arithmeticae, publicado en 1801.

Un uso familiar de la aritmética modular es su uso en el Reloj de 24 horas: la aritmética de tiempo de mantenimiento en el que el día va de medianoche a medianoche y se divide en 24 horas, numeradas del 0 al 23. Si el tiempo es ahora 19:00 - 7:00 de la tarde - entonces 8 horas más tarde será 03:00. Además podía sugerir que el tiempo después debe ser 19 + 8 = 27, pero esto no es la respuesta porque el tiempo de reloj "envuelve" al final del día. Del mismo modo, si el reloj se pone a las 12:00 (mediodía) y 21 horas transcurren, entonces el tiempo será 09:00 del día siguiente, en lugar de 33:00. Dado que el número horas comienza de nuevo cuando llega a 24, se trata de aritmética módulo 24. Cabe señalar que en este sistema no 24:00 no es una hora válida porque este es igual a la 0:00 del día siguiente, de la misma manera 2:60 es un tiempo válido porque es igual a 3: 00.

Tiempo de mantenimiento en un reloj da un ejemplo de la aritmética modular.

La relación de congruencia

La aritmética modular puede ser manejado matemáticamente mediante la introducción de una Congruencia en los números enteros que sea compatible con las operaciones de la anillo de los enteros: suma , resta y multiplicación . Para un módulo n fijo, que se define como sigue.

Dos números enteros a y b se dice que son congruentes módulo n, si su diferencia a - b es un número entero múltiplo de n. Si este es el caso, se expresa como:

$un \ equiv b \ pmod n. \,$

El enunciado matemático anterior se lee: "a es congruente con b módulo n".

Por ejemplo,

$38 \ equiv 14 \ pmod {12} \,$

porque 38-14 = 24, que es un múltiplo de 12. Para n positiva y a y b no negativo, la congruencia de A y B también puede ser pensado como la afirmación de que estos dos números tienen el mismo resto después de dividir por el módulo n. Por lo tanto,

$38 \ equiv 2 \ pmod {12} \,$

porque, cuando se divide por 12, ambos números dan 2 como resto.

La misma regla se cumple para valores negativos de una:

$-3 \ Equiv 2 \ pmod 5. \,$

Una observación en la notación: Debido a que es común a considerar varios relaciones de congruencia para diferentes módulos al mismo tiempo, el módulo se incorpora en la notación. A pesar de la notación ternaria, la relación de congruencia para un módulo dado es binario. Esto habría sido más claro si la notación a ≡ _n b se había utilizado, en lugar de la notación tradicional común.

Las propiedades que hacen de esta relación una relación de congruencia (respetando la suma, resta y multiplicación) son los siguientes.

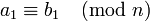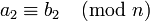Si $a_1 \ equiv b_1 \ n pmod$ y $a_2 \ equiv b_2 \ n pmod$ , Entonces:

$(A_1 + a_2) \ equiv (b_1 + b_2) \ pmod n \,$
$(A_1 - a_2) \ equiv (b_1 - b_2) \ pmod n \,$
$(A_1 a_2) \ equiv (b_1 b_2) \ pmod n \,$

El anillo de clases de congruencia

Al igual que cualquier relación de congruencia, congruencia módulo n es un relación de equivalencia , y la la clase de equivalencia de un número entero, denotado por 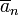$\ Overline {a} _n$ , Es el conjunto 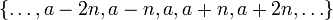$\ Left \ {\ ldots, a - 2n, a - n, a, a + n, a + 2n, \ ldots \ right \}$ . Este conjunto, que consiste de los números enteros congruentes a un módulo n, se llama la clase de congruencia o una clase de residuo de un módulo n. Otra notación para esta clase de congruencia, lo que requiere que en el contexto se conoce el módulo, es $\ Displaystyle [a]$ .

El conjunto de clases de congruencia módulo n se denota como 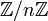$\ Mathbb {Z} / n \ mathbb {Z}$ y definida por:

$\ Mathbb {Z} / n \ mathbb {Z} = \ left \ {\ overline {a} _n | a \ in \ mathbb {Z} \ right \}.$

Cuando n ≠ 0, 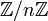$\ Mathbb {Z} / n \ mathbb {Z}$ tiene n elementos, y puede ser escrito como:

$\ Mathbb {Z} / n \ mathbb {Z} = \ left \ {\ overline {0} _n, \ overline {1} _n, \ overline {2} _n, \ ldots, \ overline {n-1} _n \ derecho \}.$

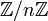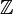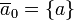Cuando n = 0, $\ Mathbb {Z} / n \ mathbb {Z}$ no tiene elementos cero; más bien, es isomorfo $\ Mathbb {Z}$ , Ya $\ Overline {a} _0 = \ left \ {a \ right \}$ .

Podemos definir la suma, resta y multiplicación en 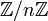$\ Mathbb {Z} / n \ mathbb {Z}$ por las siguientes reglas:

$\ Overline {a} _n + \ overline {b} _n = \ overline {a + b} _n$
$\ Overline {a} _n - \ overline {b} _n = \ overline {a - b} _n$
$\ Overline {a} _n \ overline {b} _n = \ overline {ab} _n.$

La constatación de que se trata de una definición adecuada utiliza las propiedades dadas antes.

De este modo, 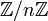$\ Mathbb {Z} / n \ mathbb {Z}$ se convierte en un anillo conmutativo . Por ejemplo, en el anillo de 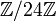$\ Mathbb {Z} / 24 \ mathbb {Z}$ , Tenemos

$\ Overline {12} _ {24} + \ overline {21} _ {24} = \ overline {9} _ {24}$

como en la aritmética para el reloj de 24 horas.

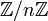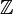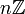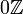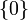La notación $\ Mathbb {Z} / n \ mathbb {Z}$ se utiliza, porque es la anillo factor $\ Mathbb {Z}$ por el ideal $n \ mathbb {Z}$ que contiene todos los enteros divisible por n, donde $0 \ mathbb {Z}$ es el conjunto unitario $\ Left \ {0 \ right \}$ .

En cuanto a los grupos, la clase de residuos 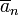$\ Overline {a} _n$ es el clase lateral de un en el grupo cociente 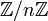$\ Mathbb {Z} / n \ mathbb {Z}$ , Un grupo cíclico .

El conjunto 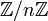$\ Mathbb {Z} / n \ mathbb {Z}$ tiene una serie de importantes propiedades matemáticas que son fundamentales para diversas ramas de las matemáticas.

En lugar de excluir el caso especial n = 0, es más útil incluir 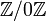$\ Mathbb {Z} / 0 \ mathbb {Z}$ (Que, como se mencionó antes, es isomorfo al anillo 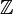$\ Mathbb {Z}$ de números enteros), por ejemplo cuando se habla de la característica de una anillo.

Residuos

La noción de la aritmética modular está relacionada con la de la resto en la división . La operación de encontrar el resto se refiere a veces como la operación de módulo y podemos ver "2 = 14 (mod 12)". La diferencia está en el uso de congruencia, indicado por ≡ e igualdad indican de =. La igualdad implica específicamente el "residuo común", el miembro menos no negativo de una clase de equivalencia. Cuando se trabaja con la aritmética modular, cada clase de equivalencia se suele representar por su residuo común, por ejemplo "38 ≡ 2 (mod 12)" que se puede encontrar utilizando división larga. De ello se desprende que, si bien es correcto decir "38 ≡ 14 (mod 12)", "2 ≡ 14 (mod 12)" y "2 ≡ 14 (mod 12)", es incorrecto decir "38 = 14 ( mod 12) "(con" = "en lugar de" ≡ ").

Los paréntesis son a veces cayeron de la expresión, por ejemplo, "38 ≡ 14 mod 12" o "2 = 14 mod 12", o se colocan alrededor del divisor por ejemplo, "38 ≡ 14 mod (12)". Tales como "38 (mod 12)" también se ha observado la notación, pero es ambiguo sin aclaración contextual.

La relación de congruencia se expresa a veces mediante el uso de módulo en lugar de mod, como "38 ≡ 14 (módulo 12)" en ciencias de la computación . La función de módulo en varios lenguajes de programación típicamente dió el residuo común, por ejemplo la declaración "y = MOD (38,12);" da y = 2.

Aplicaciones

La aritmética modular se hace referencia en la teoría de números , la teoría de grupos , la teoría de anillos, la teoría de nudos , álgebra abstracta , la criptografía , la informática , la química y las visuales y musicales artes.

Es uno de los fundamentos de la teoría de números, tocando en casi todos los aspectos de su estudio, y ofrece ejemplos clave de la teoría de grupos, teoría de anillos y el álgebra abstracta.

En criptografía, la aritmética modular sustenta directamente sistemas de clave pública, como RSA y Diffie-Hellman, así como proporcionar campos finitos que subyacen en curvas elípticas , y se utiliza en una variedad de Los algoritmos de clave simétrica que incluyen AES, IDEA, y RC4.

En ciencias de la computación, la aritmética modular se aplica a menudo en operaciones bit a bit y otras operaciones relacionadas con ancho fijo, cíclico estructuras de datos. La operación de módulo, tal como se aplica en muchos lenguajes de programación y calculadoras , es una aplicación de la aritmética modular que se utiliza a menudo en este contexto.

En química, el último dígito de la Número de registro CAS (un número que es único para cada compuesto químico) es una dígito de control, que se calcula tomando el último dígito de las dos primeras partes de la Número registrado CAS tiempos 1, los tiempos próximo dígito 2, los tiempos siguiente dígito 3, etc., sumando todos estos y el cálculo de la suma módulo 10.

En las artes visuales, la aritmética modular se puede utilizar para crear patrones artísticos basados en las tablas de multiplicación y suma módulo n (ver enlace externo, más adelante).

En la música, la aritmética módulo 12 se utiliza en la consideración del sistema de dodecafónica de temperamento igual, donde octava y equivalencia enarmónico se produce (es decir, lanzamientos en una relación de 01:02 o 02:01 son equivalentes, y C- agudo se considera la misma como D- plana).

El método de la Prueba del nueve ofrece una rápida verificación de los cálculos aritméticos decimales realizados a mano. Se basa en la aritmética modular de módulo 9, y específicamente en la propiedad crucial que 10 ≡ 1 (mod 9).

En términos más generales, la aritmética modular también tiene aplicación en disciplinas como la ley (véase, por ejemplo, distribución), la economía , (véase, por ejemplo, la teoría de juegos ) y otras zonas de la ciencias sociales, donde división proporcional y la asignación de los recursos juega una parte central del análisis.

Algunos neurólogos (véase, por ejemplo, Oliver Sacks) teorizan que los llamados sabios autistas utilizan un "innata" aritmética modular para calcular problemas tan complejos como qué día de la semana de una fecha distante caerá sobre.

Complejidad computacional

Desde la aritmética modular tiene una amplia gama de aplicaciones de este tipo, es importante saber lo difícil que es para resolver un sistema de congruencias. Un sistema lineal de congruencias se puede resolver de tiempo polinomio con una forma de eliminación de Gauss , para más detalles ver el teorema de congruencia lineal.

Resolver un sistema de ecuaciones de la aritmética modular no lineal se NP-completo. Para más detalles, véase por ejemplo MR Garey, DS Johnson: Informática y la dificultad, una Guía de la Teoría de la NP-completitud, WH Freeman 1979.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Modular_arithmetic&oldid=199402396 "