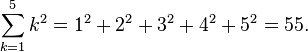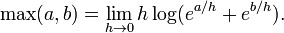Adición
Antecedentes de las escuelas de Wikipedia
Voluntarios SOS ayudaron a elegir artículos e hicieron otro material curricular SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?

Además es una operación matemática que representa la cantidad total de objetos juntos en una colección. Está representado por el signo más (+). Por ejemplo, en la imagen de la derecha, hay 3 + 2 manzanas intencionados tres manzanas y dos manzanas juntos, lo cual es un total de 5 manzanas. Por lo tanto, 3 + 2 = 5. Además de las frutas contando, además también puede representar la combinación de otras cantidades físicas y abstractas utilizando diferentes tipos de números: los números negativos , fracciones , números irracionales , vectores , decimales y más.
Además sigue varios patrones importantes. Es conmutativo , lo que significa que el orden no importa, y es asociativa , lo que significa que cuando uno agrega más de dos números, el orden en el que se lleva a cabo, además, no importa (ver Suma). Además repetida de 1 es el mismo que contando; Además de 0 no cambia un número. Además también obedece a reglas predecibles relativas a las operaciones relacionadas, como la resta y multiplicación . Todas estas reglas pueden ser probados , a partir de la adición de números naturales y generalizar a través de los números reales y más allá. General operaciones binarias que siguen estos patrones se estudian en el álgebra abstracta .
Realización de adición es una de las tareas más simples numéricos. La adición de números muy pequeños es accesible a los niños pequeños; la tarea más básica, 1 + 1, se puede realizar por los bebés tan jóvenes como de cinco meses y hasta algunos animales. En la educación primaria , los estudiantes se les enseña a sumar números en el decimal sistema, a partir de un solo dígito y abordar progresivamente los problemas más difíciles. Las ayudas mecánicas van desde el antiguo ábaco a la moderna computadora , donde la investigación sobre las implementaciones más eficientes de adición continúa hasta nuestros días.
Notación y terminología
Además está escrito utilizando el signo más "+" entre los términos; es decir, en notación infija. El resultado se expresa con una signo igual. Por ejemplo,
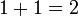 (Verbalmente, "uno más uno es igual a dos")
(Verbalmente, "uno más uno es igual a dos") 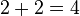 (Verbalmente, "dos más dos son cuatro")
(Verbalmente, "dos más dos son cuatro")  (Verbalmente, "tres más tres es igual a seis")
(Verbalmente, "tres más tres es igual a seis") 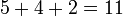 (Ver "asociatividad" de abajo )
(Ver "asociatividad" de abajo )  (Ver "multiplicación" de abajo )
(Ver "multiplicación" de abajo )
También hay situaciones en las que además se "entiende" a pesar de que no aparece ningún símbolo:

5 + 12 = 17
- Una columna de números, con el último número de la columna subrayada, por lo general indica que los números en la columna son para ser añadido, con la suma escrita a continuación en el número subrayado.
- Un número entero seguido inmediatamente por una fracción indica la suma de los dos, llamado un número mixto. Por ejemplo,
3½ = 3 + ½ = 3.5.
Esta notación puede causar confusión, ya que en la mayoría de otros contextos yuxtaposición denota multiplicación lugar.
La suma de una serie de números relacionados se puede expresar a través de notación sigma mayúscula, que denota compacta iteración. Por ejemplo,
Los números o los objetos que se añaden en general de la adición se llaman los términos, los sumandos, o los sumandos; esta terminología se traslada a la suma de varios términos. Esto es para distinguirse de factores, que se multiplican . Algunos autores llaman el primer sumando el primer sumando. De hecho, durante el Renacimiento , muchos autores no consideraron que el primer sumando un "sumando" en absoluto. Hoy en día, debido a la propiedad conmutativa de la adición, "sumando" se utiliza raramente, y ambos términos se denominan generalmente sumandos.
Toda esta terminología se deriva del latín . " Además "y" añadir "son en inglés palabras derivadas del latín addere verbo, que es a su vez un compuesto de aviso "a" y se atreven "a dar", de la Proto-indoeuropeo de la raíz * deh₃- "dar"; por lo tanto añadir es dar a. Usando el gerundio resultados sufijo -nd en "sumando", "cosa que se añadirán". Así mismo desde augere "aumentar", uno obtiene "sumando", "cosa que se incremente".

"Suma" y "sumando" deriva del latín summa sustantivo "la más alta, la parte superior" y summare verbo asociado. Esto es apropiado no sólo porque la suma de dos números positivos es mayor que cualquiera de los dos, sino porque era una vez común añadir al alza, en contra de la práctica moderna de la adición a la baja, de manera que la suma era, literalmente, más alto que los sumandos. Addere y summare se remontan al menos a Boecio, si no a los escritores romanos anteriores, como Vitruvio y Frontino; Boecio también utiliza otros términos para la operación de suma. Cuanto más tarde Términos del inglés medio "Adden" y "añadir" fueron popularizados por Chaucer .
Interpretaciones
Además se utiliza para modelar innumerables procesos físicos. Incluso para el caso simple de sumar números naturales , hay muchas interpretaciones posibles e incluso representaciones más visuales.
Combinando conjuntos
Posiblemente la interpretación más fundamental de la adición radica en la combinación de conjuntos:
- Cuando dos o más colecciones disjuntos se combinan en una sola colección, el número de objetos de la colección única es la suma de la cantidad de objetos en las colecciones originales.
Esta interpretación es fácil de visualizar, con poco peligro de ambigüedad. También es útil en las matemáticas superiores; para el definición rigurosa que inspira, ver Números naturales siguientes. Sin embargo, no es obvio cómo se debe extender esta versión de la adición para incluir números fraccionarios o números negativos.
Una solución posible es considerar las colecciones de objetos que se pueden dividir fácilmente, como pasteles o, aún mejor, segmentado barras. En lugar de simplemente la combinación de colecciones de segmentos, varillas pueden ser unidas de extremo a extremo, que ilustra otra concepción de la adición: la adición de las varillas pero no las longitudes de las varillas.
La extensión de una longitud
Una segunda interpretación de la adición proviene de una longitud inicial que se extiende por una longitud dada:
- Cuando una longitud original se prolonga por una cantidad dada, la longitud final es la suma de la longitud original y la longitud de la extensión.


La suma A + B se puede interpretar como una operación binaria que combina a y b, en un sentido algebraico, o puede ser interpretado como la adición de más unidades de b a a. Bajo la última interpretación, las partes de una suma a + b desempeñan papeles asimétricos, y la operación a + b es visto como la aplicación de la operación unaria + b a a. En lugar de llamar tanto A como B sumandos, es más apropiado para llamar a un el primer sumando en este caso, ya que una juega un papel pasivo. El punto de vista unitario también es útil cuando se habla de la resta , ya que cada operación unario tiene una operación de resta unaria inversa, y viceversa.
Propiedades
Conmutatividad

La adición es conmutativa , lo que significa que uno puede invertir los términos en una suma de izquierda a derecha, y el resultado es el mismo que el último. Simbólicamente, si ayb son dos números cualesquiera, entonces
- a + b = b + a.
El hecho de que la adición es conmutativa es conocida como la "ley conmutativa de la suma". Esta frase sugiere que hay otras leyes conmutativas: por ejemplo, hay una ley conmutativa de la multiplicación. Sin embargo, muchos operaciones binarias no son conmutativa, como la resta y la división, por lo que es engañoso hablar de una "ley conmutativa" sin reservas.
Asociatividad

Una propiedad un tanto más sutil de la adición es la asociatividad , que surge cuando se trata de definir la suma repetida. En caso de que la expresión
- "A + b + c"
ser definido para significar (a + b) + c o a + (b + c)? Esta adición es asociativa nos dice que la elección de la definición es irrelevante. Para cualquiera de los tres números a, b, y c, es cierto que
- (A + b) + c = a + (b + c).
Por ejemplo, (1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2 + 3). No todas las operaciones son asociativas, así que en expresiones con otras operaciones como la resta, es importante especificar el orden de las operaciones.
Elemento de identidad

Cuando la adición de cero a cualquier número, la cantidad no cambia; cero es el elemento de identidad para la adición, también conocido como el identidad aditiva. En símbolos, para todo a,
- a + 0 = 0 + a = a.
Esta ley fue identificado por primera vez en Brahmagupta de Brahmasphutasiddhanta en el 628 dC, aunque él lo escribió como tres leyes distintas, dependiendo de si a es negativo, positivo o cero en sí, y usó palabras en lugar de símbolos algebraicos. Más tarde Matemáticos indios refinaron el concepto; alrededor del año 830, Mahavira escribió, "cero se convierte en lo mismo que lo que se añade a la misma", correspondiente a la declaración unario 0 + a = a. En el siglo 12, Bhaskara escribió: "En la adición de cifrado, o sustracción de la misma, la cantidad, positivo o negativo, sigue siendo el mismo", correspondiente a la declaración unario a + 0 = a.
Sucesor
En el contexto de los números enteros, la adición de uno también desempeña un papel especial: para cualquier número entero a, el número entero (a + 1) es el menor entero mayor que A, también conocido como el sucesor de un. Debido a esta sucesión, el valor de algunos a + b también puede ser visto como el 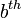 sucesor de una, por lo que además de la sucesión reiteró.
sucesor de una, por lo que además de la sucesión reiteró.
Unidades
Para agregar numéricamente las magnitudes físicas con unidades, primero deben ser expresados con unidades comunes. Por ejemplo, si una medida de 5 pies se extiende por 2 pulgadas, la suma es 62 pulgadas, desde 60 pulgadas es sinónimo de 5 pies. Por otro lado, por lo general es de sentido para tratar de añadir 3 metros y 4 metros cuadrados, ya que esas unidades son incomparable; este tipo de consideración es fundamental en análisis dimensional.
Además Escénicas
Habilidad innata
Los estudios sobre el desarrollo matemático que empiezan alrededor de la década de 1980 se han aprovechado el fenómeno de la habituación: los bebés se vean más largas en situaciones que son inesperados. Un experimento seminal por Karen Wynn en 1992 la participación de Mickey Mouse muñecos manipulados detrás de una pantalla demostró que los bebés de cinco meses de edad esperan que 1 + 1 es 2, y son comparativamente sorprendido cuando una situación física parece implicar que 1 + 1 es 1 o 3. Este hallazgo ya ha sido afirmado por diversos laboratorios que utilizan diferentes metodologías. Otro experimento 1992 con más viejo niños pequeños, de entre 18 y 35 meses, explotaron su desarrollo de control de motor por lo que les permite recuperar de ping-pong bolas de una caja; los más jóvenes respondieron bien para los números pequeños, mientras que los sujetos de edad avanzada fueron capaces de calcular sumas de hasta 5.
Incluso algunos animales no humanos muestran una capacidad limitada para agregar, en particular primates. En un experimento de 1995 imitando 1992 resultado de Wynn (pero utilizando berenjenas en lugar de muñecas), macacos rhesus y tamarinos cottontop un comportamiento similar a los bebés humanos. Más dramáticamente, después de haber sido enseñado el significado de los números arábigos del 0 al 4, uno chimpancé era capaz de calcular la suma de dos números sin más formación.
Descubriendo además como hijos
Por lo general, los niños primero dominar contando. Cuando se le presente un problema que requiere que los dos artículos y tres artículos pueden combinar, los niños pequeños modelar la situación con los objetos físicos, a menudo los dedos o un dibujo, y luego contar el total. A medida que adquieren experiencia, aprenden o descubrir la estrategia de "contar-on": le pide que encuentre dos más tres, los niños cuentan dos y tres, diciendo "tres, cuatro, cinco" (usualmente marcando los dedos), y llegando a las cinco . Esta estrategia parece casi universal; los niños pueden fácilmente recogerlo de sus compañeros o profesores. La mayoría descubren de forma independiente. Con más experiencia, los niños aprenden a sumar más rápidamente aprovechando la conmutatividad de la suma contando desde el número mayor, en este caso a partir de tres y contando "cuatro, cinco." Finalmente los niños comienzan a recordar algunos hechos de adición (" bonos de números "), ya sea a través de la experiencia o la memorización. Una vez que algunos hechos son cometidos a la memoria, los niños empiezan a derivar hechos desconocidos de conocidos. Por ejemplo, un niño pidió que añadir seis y siete pueden saber que el 6 + 6 = 12 y entonces la razón de que 6 + 7 es uno más, o 13. Tales hechos derivados se pueden encontrar muy rápidamente y estudiante de la escuela más elemental eventualmente se basan en una mezcla de hechos memorizados y derivados añadir fluidez.
Sistema Decimal
El requisito previo a la adición en el decimal sistema es el recuerdo con fluidez o derivación de las "operaciones de suma" 100 de un solo dígito. Uno podria memorizar todos los hechos por estrategias memorísticas, pero basadas en patrones son más esclarecedor y, para la mayoría de la gente, más eficiente:
- Propiedad conmutativa: se mencionó anteriormente, utilizando el patrón de a + b = b + a reduce el número de "operaciones de suma» de 100 a 55.
- Uno o dos más: Adición de 1 o 2 es una tarea básica, y puede lograrse a través de contar con o, en última instancia, intuición.
- Zero: Desde el cero es la identidad aditiva, agregando cero es trivial. No obstante, en la enseñanza de la aritmética, algunos estudiantes son introducidos a la adición como un proceso que siempre aumenta los sumandos; problemas de palabras pueden ayudar a racionalizar la "excepción" de cero.
- Dobles: Adición de un número a sí mismo tiene que ver con contar por dos y de multiplicación . Dobles hechos forman una columna vertebral de muchos hechos relacionados, y los estudiantes los encuentran relativamente fácil de entender.
- Cerca-dobles: Sumas como 6 + 7 = 13 se pueden derivar rápidamente en el hecho de dobles 6 + 6 = 12 añadiendo uno más, o de 7 + 7 = 14, pero restando uno.
- Cinco y diez: Sumas de la forma 5 + x 10 + x por lo general se memorizan temprana y se puede utilizar para derivar otros hechos. Por ejemplo, 6 + 7 = 13 se pueden derivar de 5 + 7 = 12 mediante la adición de uno más.
- Hacer diez: Una estrategia de avanzada utiliza 10 como producto intermedio para sumas que incluyen 8 o 9; por ejemplo, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14.
Como los estudiantes crecen, cometen más hechos a la memoria, y aprender a derivar otros hechos rápidamente y con fluidez. Muchos estudiantes nunca se comprometen todos los hechos en la memoria, pero aún pueden encontrar cualquier hecho básico rápidamente.
El algoritmo estándar para añadir números de varios dígitos es alinear los sumandos verticalmente y agregue las columnas, a partir de la columna de los de la derecha. Si una columna es superior a diez, el dedo adicional es " llevó "en la siguiente columna Una estrategia alternativa se inicia la adición de el dígito más significativo a la izquierda;.. esta ruta hace que llevar un poco torpe, pero es más rápido en conseguir una estimación aproximada de la suma Hay muchos otros métodos alternativos.
- Fracción: Adición
- La notación científica: Operaciones
Computadoras

Los ordenadores analógicos trabajan directamente con las cantidades físicas, por lo que sus mecanismos de adición dependen de la forma de los sumandos. Un sumador mecánica podría representar dos sumandos como las posiciones de los bloques de deslizamiento, en cuyo caso se pueden añadir con un promedio palanca. Si los sumandos son las velocidades de rotación de dos ejes, se pueden añadir con una diferencial. Una víbora hidráulico puede añadir el presiones en dos cámaras por la explotación de la segunda ley de Newton para equilibrar fuerzas en una asamblea de pistones. La situación más común que una computadora analógica de propósito general es agregar dos voltajes (por referencia al suelo); esto se puede lograr más o menos con una resistor red, pero un mejor diseño aprovecha una amplificador operacional.
Además también es fundamental para el funcionamiento de los ordenadores digitales , donde la eficiencia de adición, en particular el llevar mecanismo, es una limitación importante para el rendimiento general.

Acciones de adición, calculadoras mecánicas cuya función principal era Además, fueron los primeros equipos automáticos, digitales. 1623 Reloj Cálculo de Wilhelm Schickard podía sumar y restar, pero fue severamente limitado por un mecanismo de transporte torpe. Quemado durante su construcción en 1624 y desconocido para el mundo durante más de tres siglos, fue redescubierto en 1957 y por lo tanto no tuvo impacto en el desarrollo de calculadoras mecánicas. Blaise Pascal inventó la calculadora mecánica en 1642 con un mecanismo de transporte por gravedad asistido ingeniosa . Calculadora de Pascal estaba limitado por su mecanismo de transporte en un sentido diferente: sus ruedas se volvió una sola manera, por lo que podría añadir, pero no restar, excepto por el método de complementos. Por 1674 Gottfried Leibniz hizo el primer multiplicador mecánico; aún así fue accionado, si no motivada, por adición.

Culebras ejecutan además de enteros en los ordenadores digitales electrónicos, normalmente utilizando la aritmética binaria . La arquitectura más simple es el acarreo del sumador ondulación, que sigue el algoritmo de varios dígitos estándar. Una ligera mejora es la llevar el diseño de salto, de nuevo siguiendo la intuición humana; uno no lleva a cabo todos los acarreos en el cálculo de 999 + 1, pero uno no pasa por el grupo de 9s y salta a la respuesta.
Puesto que calculan dígitos uno a la vez, los métodos anteriores son demasiado lento para la mayoría de los propósitos modernos. En las computadoras digitales modernas, además de número entero es típicamente la instrucción aritmética más rápida, sin embargo, tiene el mayor impacto en el rendimiento, ya que la base de toda la operaciones de punto flotante, así como tareas tan básicas como Generación de Direcciones durante de acceso a memoria y ir a buscar instrucciones durante ramificación. Para aumentar la velocidad, diseños modernos calculan en cifras paralelo; estos planes van por nombres tales como llevar a seleccionar, llevar búsqueda hacia delante, y la Pseudocarry Ling. Casi todas las implementaciones modernas son, de hecho, los híbridos de estos tres últimos diseños.
A diferencia de adición en papel, además de un equipo a menudo cambia los sumandos. En el antiguo ábaco y añadiendo bordo, ambos sumandos son destruidas, dejando sólo la suma. La influencia del ábaco en el pensamiento matemático era lo suficientemente fuerte que los primeros latinos textos menudo afirmaban que en el proceso de añadir "un número a un número", ambos números se desvanecen. En los tiempos modernos, la instrucción ADD de un microprocesador reemplaza el primer sumando con la suma, pero conserva el sumando. En un lenguaje de programación de alto nivel, la evaluación a + b no cambia o B; si el objetivo es reemplazar una con la suma este debe ser solicitado expresamente, por lo general con la declaración a = a + b. Algunos lenguajes como C o C ++ permiten que esto se abrevia como a + b =.
La adición de números naturales y reales
Para demostrar las propiedades usuales de suma, primero hay que definir además para el contexto en cuestión. Además se definió por primera vez en los números naturales . En la teoría de conjuntos , la suma se extiende entonces a conjuntos cada vez más grandes que incluyen los números naturales: los números enteros , los números racionales y los números reales . (En enseñanza de las matemáticas, se añaden las fracciones positivas antes de los números negativos son aún considerados; esta es también la ruta histórica)
Números naturales
Hay dos formas populares para definir la suma de dos números naturales a y b. Si uno define los números naturales para ser las cardinalidades de conjuntos finitos, (la cardinalidad de un conjunto es el número de elementos en el conjunto), entonces es apropiado para definir la suma de la siguiente manera:
- Sea N (S) sea la cardinalidad de un conjunto S. Tomar dos conjuntos disjuntos A y B, con N (A) = A y N (B) = b. A continuación, a + b se define como
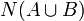 .
.
Aquí, A U B es el unión de A y B. Una versión alterna de esta definición permite que A y B para posiblemente se superponen y luego toma su unión de la desunión, un mecanismo que permite a los elementos comunes que se separan y por lo tanto cuentan dos veces.
La otra definición popular es recursivo:
- Sea n + ser la sucesor de n, que es el siguiente número de n en los números naturales, así + 0 = 1, 1 = 2 +. Definir a + 0 = a. Definir la suma general de forma recursiva por un + (b +) = (a + b) +. Por lo tanto 1 + 1 = 1 + 0 + = (1 + 0) + = + 1 = 2.
Una vez más, hay pequeñas variaciones sobre esta definición en la literatura. Tomado literalmente, la definición anterior es una aplicación de la La recursividad Teorema sobre la poset N2. Por otro lado, algunas fuentes prefieren utilizar un teorema de recursión restringida que sólo se aplica al conjunto de números naturales. Entonces se considera una para ser temporalmente "fijo", se aplica la recursividad en b para definir una función "a +", y pastas de estas operaciones unarios para todo un conjunto para formar la operación binaria completa.
Esta formulación recursiva de adición fue desarrollada por Dedekind ya en 1854, y que se expandiría sobre él en las siguientes décadas. Él demostró las propiedades asociativas y conmutativas, entre otros, a través de inducción matemática; Para ejemplos de tales pruebas inductivas, consulte Adición de números naturales .
Enteros

La concepción más simple de un número entero es que se compone de un valor absoluto (que es un número natural) y una firmar (generalmente ya sea positivo o negativo ). El entero cero es un tercer caso especial, que no es ni positivo ni negativo. La definición correspondiente de adición debe proceder por casos:
- Para un entero n, sea | n | ser su valor absoluto. Vamos a y b son enteros. Si A o B es cero, lo tratan como una identidad. Si ayb son ambos positivos, definir a + b = | a | + | b |. Si a y b son ambos negativos, definir a + b = - (| a | + | b |). Si A y B tienen diferentes signos, definir un B + a ser la diferencia entre | a | y | b |, con el signo del término cuyo valor absoluto es mayor.
Aunque esta definición puede ser útil para problemas concretos, es demasiado complicado de producir pruebas generales elegantes; hay demasiados casos a considerar.
Una concepción mucho más conveniente de los números enteros es el Construcción grupo de Grothendieck. La observación esencial es que cada número entero se puede expresar (no exclusiva) como la diferencia de dos números naturales, por lo que puede así definir un número entero como la diferencia de dos números naturales. Además se define entonces para ser compatible con la resta:
- Dados dos números enteros a - b y c - d, donde a, b, c, y d son números naturales, definir (a - b) + (c - d) = (a + c) - (b + d).
Números racionales (fracciones)
La adición de los números racionales se puede calcular utilizando la mínimo común denominador, pero una definición conceptualmente más simple implica única adición y multiplicación de enteros:
- Definir
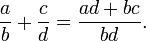
La conmutatividad y asociatividad de la adición racional es una consecuencia fácil de las leyes de la aritmética de enteros. Para un análisis más riguroso y general, véase campo de fracciones.
Los números reales

Una construcción común del conjunto de números reales es la finalización Dedekind del conjunto de los números racionales. Un número real se define como una Dedekind corte de los racionales: una conjunto no vacío de los racionales que está cerrado hacia abajo y no tiene mayor elemento. La suma de los números reales a y b se define elemento por elemento:
- Definir

Esta definición fue publicado por primera vez, en una forma ligeramente modificada, por Richard Dedekind en 1872. La conmutatividad y asociatividad de la suma de bienes son inmediatos; definir el verdadero número 0 que es el conjunto de números racionales negativos, se ve fácilmente la identidad aditiva. Probablemente la parte más delicada de esta construcción perteneciente a la adición es la definición de inversos aditivos.

Por desgracia, se trata de la multiplicación de cortes de Dedekind es una pesadilla caso por caso similar a la adición de enteros con signo. Otro enfoque es la finalización métrica de los números racionales. Un número real está esencialmente define como el límite de una Sucesión de Cauchy de números racionales, lim a n. Además se define término a término:
- Definir
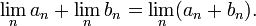
Esta definición fue publicado por primera vez por Georg Cantor , también en 1872, aunque su formalismo fue un poco diferente. Hay que demostrar que está bien definido esta operación, que trata de secuencias de co-Cauchy. Una vez que se hace esta tarea, todas las propiedades de la suma real, siguen inmediatamente de las propiedades de los números racionales. Además, las otras operaciones aritméticas, incluyendo la multiplicación, tienen, definiciones análogas directas.
Las generalizaciones
- Hay muchas cosas que se pueden agregar: números, vectores, matrices, espacios, formas, sistemas, funciones, ecuaciones, cuerdas, cadenas ... - Alexander Bogomolny
Hay muchas operaciones binarias que se pueden ver como generalizaciones de la operación de suma de los números reales. El campo de la álgebra abstracta se preocupa especialmente por tales operaciones generalizadas, y que también aparece en la teoría de conjuntos y la teoría de categorías.
Además en álgebra abstracta
En álgebra lineal , un espacio vectorial es una estructura algebraica que permite la adición de cualquiera de dos vectores y para la ampliación vectores. Un espacio vectorial familiar es el conjunto de todos los pares ordenados de números reales; el par ordenado (a, b) se interpreta como un vector desde el origen en el plano euclidiano hasta el punto (a, b) en el plano. La suma de dos vectores se obtiene mediante la adición de sus coordenadas individuales:
- (A, b) + (c, d) = (a + c, b + d).
Esta operación, además es fundamental para la mecánica clásica , en la que los vectores se interpretan como fuerzas .
En la aritmética modular , el conjunto de enteros módulo 12 tiene doce elementos; hereda una operación de suma de los números enteros que es fundamental para la teoría de conjuntos musicales. El conjunto de los enteros módulo 2 tiene sólo dos elementos; la operación de suma hereda es conocido en la lógica booleana como el " exclusiva o "función. En geometría , la suma de dos medidas de los ángulos se toma a menudo para ser su suma como números reales módulo 2π. Esto equivale a una operación de suma en el círculo , que a su vez se generaliza a las operaciones de suma en muchas dimensiones tori .
La teoría general de álgebra abstracta permite una operación de "adición" al ser cualquier asociativa y conmutativa operación en un conjunto. Básicos estructuras algebraicas con tal operación Además incluyen monoides conmutativa y grupos abelianos.
Además, en la teoría de conjuntos y la teoría de la categoría
Una generalización de largo alcance de la suma de los números naturales es la adición de números ordinales y cardinales en la teoría de conjuntos. Estos dan dos generalizaciones diferentes de la suma de números naturales a la transfinito. A diferencia de la mayoría de las operaciones de suma, además de los números ordinales no es conmutativa. La adición de los números cardinales, sin embargo, es una operación conmutativa estrechamente relacionado con el operación de unión de la desunión.
En la teoría de categorías, unión disjunta es visto como un caso particular de la operación co-producto, y coproductos generales son, quizás, la más abstracta de todas las generalizaciones de adición. Algunos coproductos, tales como Suma directa y Suma Wedge, se nombran para evocar su conexión con la adición.
Las operaciones vinculadas
Aritmética
La resta se puede considerar como un tipo de adición, es decir, la adición de una inverso aditivo. La resta es en sí mismo una especie de inversa de la adición, en que la adición de x y restando x son funciones inversas .
Dado un conjunto con una operación de suma, no siempre se puede definir una operación de resta correspondiente en ese conjunto; el conjunto de los números naturales es un ejemplo sencillo. Por otra parte, una operación de resta determina de forma única una operación de suma, una operación inversa aditivo, y una identidad aditivo; Por esta razón, un grupo aditivo puede ser descrito como un conjunto que se cierra en virtud de la resta.
La multiplicación se puede considerar además como repetida. Si un solo término x aparece en una suma n veces, entonces la suma es el producto de n y x. Si n no es un número natural , el producto todavía puede tener sentido; por ejemplo, la multiplicación por -1 Se obtiene el inverso aditivo de un número.

En los números reales y complejos, la suma y la multiplicación se pueden intercambiar por la función exponencial :
- e a + b = e un e b.
Esta identidad permite la multiplicación para ser llevada a cabo mediante la consulta de una tabla de logaritmos y además la informática con la mano; sino que también permite la multiplicación en una regla de calculo. La fórmula sigue siendo una buena aproximación de primer orden en el contexto amplio de Grupos de Lie, donde se relaciona la multiplicación de los elementos del grupo infinitesimales con adición de vectores en el asociado Acuéstese álgebra.
Hay aún más generalizaciones de la multiplicación de adición. En general, las operaciones de multiplicación siempre distribuir sobre la suma; este requisito se formaliza en la definición de un anillo. En algunos contextos, tales como los números enteros, distributividad sobre la suma y la existencia de una identidad multiplicativa es suficiente para determinar de forma exclusiva la operación de multiplicación. La propiedad distributiva también proporciona información acerca de adición; mediante la expansión del producto (1 + 1) (a + b) en ambos sentidos, se concluye que la adición se ve obligado a ser conmutativa. Por esta razón, la adición anillo es conmutativo en general.
División es una operación aritmética remotamente relacionado con adición. Desde a / b = a (b-1), la división es distributiva derecho sobre la suma: (a + b) / c = a / c + b / c. Sin embargo, la división no se deja distributiva sobre la adición; 1 / (2 + 2) no es el mismo que 1/2 + 1/2.
Ordenando

El funcionamiento máximo "max (a, b)" es una operación binaria similar a la adición. De hecho, si dos números no negativos a y b son de diferente órdenes de magnitud, entonces su suma es aproximadamente igual al máximo. Esta aproximación es extremadamente útil en las aplicaciones de las matemáticas, por ejemplo, en truncar la serie de Taylor . Sin embargo, presenta una dificultad perpetua en análisis numérico, en esencia, ya que "max" no es invertible. Si b es mucho mayor que a, entonces un cálculo directo de (a + b) - b puede acumular una inaceptable error de redondeo, quizás incluso volver a cero. Ver también La pérdida de importancia.
La aproximación es exacta en una especie de límite infinito; si A o B es un infinito número cardinal , su suma cardinal es exactamente igual a la mayor de las dos. Por consiguiente, no hay ninguna operación de resta para cardenales infinitos.
Maximización es conmutativa y asociativa, como adición. Además, puesto que la adición conserva el orden de los números reales, la adición se distribuye sobre "max" de la misma manera que la multiplicación se distribuye sobre la suma:
- a + max (b, c) = max (a + b, a + c).
Por estas razones, en tropical geometría uno reemplaza con la adición de multiplicación y adición con maximización. En este contexto, además se llama "multiplicación tropical", la maximización se llama "Además tropical", y la "identidad aditiva" tropical es infinito negativo. Algunos autores prefieren para sustituir además con la minimización; entonces la identidad aditiva es infinito positivo.
Atar estas observaciones en conjunto, además tropical está aproximadamente relacionada con la adición regular a través del logaritmo :
- log (a + b) ≈ máx (log un log b),
que se vuelve más precisa como la base del logaritmo aumenta. La aproximación se puede hacer exacto por la extracción de una h constante, llamado por analogía con La constante de Planck de la mecánica cuántica , y tomando la " límite clásico "cuando h tiende a cero:
En este sentido, la operación máxima es de undescuantificadaversión de adición.
Otras formas de añadir
Incremento, también conocida como laoperación sucesor, es la adición de1a un número.
Suma describe la adición de muchos números arbitrariamente, por lo general más de sólo dos. Incluye la idea de la suma de un número único, que es en sí, y la suma vacío, que es cero . Una suma infinita es un procedimiento delicado conocido como una serie.
Contandoun conjunto finito es equivalente a la suma de 1 sobre el conjunto.
Integración es una especie de "suma" más de un continuum, o más precisamente y, en general, más de un diferenciable colector . Integración sobre un colector de cero-dimensional se reduce a la suma.
Combinaciones lineales combinan la multiplicación y la suma; que son sumas en la que cada término tiene un multiplicador, por lo general un verdadero o complejo número. Combinaciones lineales son especialmente útiles en contextos en los que además de sencilla violaría alguna regla de normalización, tales como la mezcla de estrategias en la teoría de juegos o superposición de estados de la mecánica cuántica .
Convolución se utiliza para agregar dos independientes variables aleatorias definidas por funciones de distribución . Su definición usual combina la integración, resta y multiplicación. En general, la convolución es útil como un tipo de adición del lado de dominio; por el contrario, la suma de vectores es un tipo de adición del lado del rango.
En la literatura
- En el capítulo 9 de Lewis Carroll A través del espejo , la Reina Blanca pide a Alicia, "y usted Adición? ... ¿Cuál es uno y uno y uno y uno y uno y uno y uno y uno y uno y uno?" Alicia admite que ella perdió la cuenta, y la Reina Roja declara: "Ella no puede hacer Adición".
- En De George Orwell Mil novecientos ochenta y cuatro , el valor de 2 + 2 se pone en duda; el Estado sostiene que si se declara 2 + 2 = 5, entonces es así. Ver Dos más dos son cinco para la historia de esta idea.