Mecanica cuantica

Temas relacionados: Ciencia

Antecedentes de las escuelas de Wikipedia

SOS Children hizo esta selecci??n Wikipedia junto a otros recursos de escuelas . SOS Children ha cuidado de ni??os en ??frica durante cuarenta a??os. ??Puedes ayudar a su trabajo en ??frica ?

Mecanica cuantica
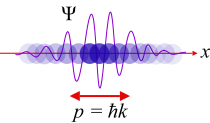La dualidad onda-part??cula
Introducci??n Glosario ?? Historia
Fondo La notaci??n del Sujetador-ket La mec??nica cl??sica Hamiltoniano Interferencia La teor??a cu??ntica Viejo
Conceptos fundamentales Complementariedad La decoherencia La no localidad Estado cu??ntico Superposici??n T??neles Incertidumbre Funci??n de onda
Experimentos La desigualdad de Bell Davisson-Germer Elecci??n retardada borrador cu??ntico Doble rendija Franck-Hertz experimento Entre Mach-Zehnder. Elitzur-Vaidman Corchete Goma de borrar Quantum El gato de Schr??dinger Stern-Gerlach Elecci??n retardada de Wheeler
Formulaciones Formulaciones Heisenberg Interacci??n Mec??nica matricial Schr??dinger Suma de historias El espacio de fase
Ecuaciones Dirac Klein-Gordon Pauli Rydberg Schr??dinger
Interpretaciones Interpretaciones (resumen) Conciencia-causado Historias consistentes Copenhague De Broglie-Bohm Conjunto Variables ocultas Muchos mundos Colapso Objetivo Pondicherry L??gica cu??ntica Relacional Estoc??stico Transaccional
Temas avanzados Caos cu??ntico Teor??a cu??ntica de campos Ciencia de la informaci??n cu??ntica Teor??a de la dispersi??n La mec??nica cu??ntica fraccionarios
Los cient??ficos Campana Blackett Bogolyubov Bohm Bohr Bardeen Nacido Bose De Broglie Compton Tonelero Dirac Dyson Davisson Duarte Debye Ehrenfest Einstein Everett Fock Fermi Feynman Hertz Heisenberg Hilbert Jordania Klitzing Kusch Kramers von Neumann Pauli Cordero Laue Laughlin Moseley Millikan Onnes Planck Raman Rydberg Salam Schr??dinger St??rmer Shockley Schrieffer Shull Sommerfeld Thomson Tsui Tomonaga Weyl Sala Wien Wigner Zeeman Zeilinger

Fig. 1: Densidades de probabilidad correspondiente a la funciones de onda de un electr??n en una ??tomo de hidr??geno que posee definida de energ??a (incrementando la baja: n = 1, 2, 3, ...) y el momento angular (aumentando a trav??s de: s, p, d, ...). Las ??reas m??s brillantes corresponden a una mayor densidad de probabilidad para una medici??n de la posici??n. Funciones de onda como ??stas son directamente comparables con Figuras de Chladni de modos ac??sticos de las vibraciones en la f??sica cl??sica y de hecho son modos de oscilaci??n as??: poseen una fuerte de energ??a y por lo tanto un gran frecuencia. El momento angular y la energ??a son cuantificada, y s??lo tomar valores discretos como los que se muestran (como es el caso de frecuencias de resonancia en ac??stica).

La mec??nica cu??ntica es el estudio de sistemas mec??nicos cuyas dimensiones son cerca o por debajo de la at??mica escala, tales como mol??culas , ??tomos , electrones , protones y otros part??culas subat??micas. La mec??nica cu??ntica es una rama fundamental de la f??sica con amplias aplicaciones. La teor??a cu??ntica generaliza la mec??nica cl??sica y ofrece descripciones precisas para muchos previamente inexplicable fen??menos tales como la radiaci??n del cuerpo negro y estable ??rbitas de los electrones. Los efectos de la mec??nica cu??ntica t??picamente no son observables en escalas macrosc??picas, pero se hacen evidentes en el at??mica y nivel subat??mico. Sin embargo, hay excepciones a esta regla, como superfluidez.

Visi??n de conjunto

La palabra "quantum" proviene de la palabra latina que significa "lo grande" o "cu??nto". En la mec??nica cu??ntica, se refiere a una unidad discreta que la teor??a cu??ntica asigna a ciertas cantidades f??sicas, tales como la energ??a de un ??tomo en reposo (v??ase la Figura 1, a la derecha). El descubrimiento de que las olas tienen paquetes discretos de energ??a (llamado quanta) que se comportan de una manera similar a part??culas llevaron a la rama de la f??sica que se ocupa de los sistemas at??micos y subat??micos que hoy llamamos la mec??nica cu??ntica. Es la subyacente matem??tica marco de muchos campos de la f??sica y la qu??mica , incluyendo la f??sica de la materia condensada , la f??sica de estado s??lido, la f??sica at??mica , f??sica molecular , la qu??mica computacional , qu??mica cu??ntica , la f??sica de part??culas y f??sica nuclear . Los fundamentos de la mec??nica cu??ntica se establecieron durante la primera mitad del siglo XX por Werner Heisenberg, Max Planck , Louis de Broglie, Albert Einstein , Niels Bohr , Erwin Schrodinger, Max Born, John von Neumann , Paul Dirac , Wolfgang Pauli y otros. Todav??a se estudian activamente Algunos aspectos fundamentales de la teor??a.

La mec??nica cu??ntica es esencial para entender el comportamiento de los sistemas en at??micas escalas de longitud y m??s peque??o. Por ejemplo, si la mec??nica newtoniana rigen el funcionamiento de un ??tomo, los electrones ser??an r??pidamente viajar hacia y chocan con el n??cleo , haciendo ??tomos estables imposible. Sin embargo, en el mundo natural los electrones permanecen normalmente en una trayectoria orbital alrededor del n??cleo desconocido, desafiando electromagnetismo cl??sico.

La mec??nica cu??ntica se desarroll?? inicialmente para proporcionar una mejor explicaci??n del ??tomo, en especial el Los espectros de la luz emitida por diferentes especies at??micas . La teor??a cu??ntica del ??tomo fue desarrollado como una explicaci??n de permanencia del electr??n en su orbital, que no pod??a explicarse por las leyes del movimiento de Newton y por las leyes de Maxwell del electromagnetismo cl??sico.

En el formalismo de la mec??nica cu??ntica, el estado de un sistema en un momento dado se describe por un complejo funci??n de onda (a veces referido como orbitales en el caso de los electrones at??micos), y m??s generalmente, los elementos de un complejo espacio vectorial . Este objeto matem??tico abstracto permite el c??lculo de las probabilidades de los resultados de los experimentos concretos. Por ejemplo, se le permite a uno calcular la probabilidad de encontrar un electr??n en una regi??n particular alrededor del n??cleo en un momento particular. Al contrario de la mec??nica cl??sica, nunca se puede hacer predicciones simult??neas de variables conjugadas, como la posici??n y el momento, con una precisi??n arbitraria. Por ejemplo, los electrones pueden ser considerados para ser ubicado en alg??n lugar dentro de una regi??n de espacio, pero con ser desconocido sus posiciones exactas. Contornos de probabilidad constante, a menudo referido como "nubes" se pueden extraer alrededor del n??cleo de un ??tomo de conceptualizar donde el electr??n podr??a ubicarse con m??s probabilidad. Heisenberg principio de incertidumbre cuantifica la imposibilidad de localizar con precisi??n la part??cula.

El otro ejemplar que condujo a la mec??nica cu??ntica fue el estudio de las ondas electromagn??ticas , tales como luz. Cuando se descubri?? en 1900 por Max Planck que la energ??a de las olas podr??a ser descrito como un conjunto de peque??os paquetes o cuantos, Albert Einstein explotado esta idea para mostrar que una onda electromagn??tica tal como la luz puede ser descrito por una part??cula llamada fot??n con una discreto de energ??a depende de su frecuencia. Esto condujo a una teor??a de la unidad entre las part??culas subat??micas y las ondas electromagn??ticas llamadas la dualidad onda-part??cula en el que part??culas y ondas eran ni lo uno ni lo otro, pero ten??a ciertas propiedades de ambos. Si bien la mec??nica cu??ntica describe el mundo de lo muy peque??o, tambi??n es necesario para explicar ciertos " sistemas cu??nticos macrosc??picos ", tales como los superconductores y superfluidos.

En t??rminos generales, la mec??nica cu??ntica incorpora cuatro clases de fen??menos que la f??sica cl??sica no puede dar cuenta de: (i) la cuantificaci??n (discretizaci??n) de ciertas cantidades f??sicas, (ii) la dualidad onda-part??cula , (iii) la principio de incertidumbre, y (iv) entrelazamiento cu??ntico. Cada uno de estos fen??menos se describe en detalle en las secciones siguientes.

Historia

La historia de la mec??nica cu??ntica comenz?? esencialmente con el descubrimiento de 1838 los rayos cat??dicos por Michael Faraday , la declaraci??n 1859 de la problema de la radiaci??n del cuerpo negro por Gustav Kirchhoff, la sugerencia de 1877 Ludwig Boltzmann que los estados de energ??a de un sistema f??sico podr??a ser discreto, y la hip??tesis cu??ntica 1900 por Max Planck que cualquier energ??a se irradia y se absorbe en cantidades divisibles por "elementos de energ??a 'discretas, E, de tal manera que cada uno de estos elementos de energ??a es proporcional al frecuencia ν con la que cada uno de ellos individualmente irradian energ??a , tal como se define por la siguiente f??rmula:

$E = h \ nu = \ hbar \ omega \,$

donde h es Acci??n constante de Planck. Aunque Planck insistido en que esto era simplemente un aspecto de la absorci??n y la radiaci??n de la energ??a y no ten??a nada que ver con la realidad f??sica de la propia energ??a, en 1905, para explicar el efecto fotoel??ctrico (1839), es decir, que la luz de ciertos materiales que brilla puede funcionar para expulsar los electrones de la materia, Albert Einstein postul??, como sobre la base de la hip??tesis cu??ntica de Planck, que la luz en s?? consiste en cuantos individuales, que m??s tarde lleg?? a ser llamado fotones (1926 ). Desde la simple postulaci??n de Einstein fue transmitida por una r??faga de debatir, teorizando y pruebas, y por lo tanto, todo el campo de la f??sica cu??ntica .

La relatividad y la mec??nica cu??ntica

El mundo moderno de la f??sica se fund?? principalmente en dos teor??as probadas y demostrable de sonido de la relatividad general y la mec??nica cu??ntica -theories que parecen contradecirse entre s??. Los postulados que definen la teor??a de la relatividad y la teor??a cu??ntica, tanto de Einstein son indiscutiblemente apoyadas por evidencia emp??rica rigurosa y repetida. Sin embargo, mientras no se contradicen directamente entre s?? en teor??a (por lo menos en lo que respecta a las reclamaciones de primaria), son resistentes a ser incorporados dentro de un modelo coherente.

El mismo Einstein es bien conocido por rechazar algunas de las afirmaciones de la mec??nica cu??ntica. Aunque es evidente que la invenci??n en este campo, no aceptaba las consecuencias y las interpretaciones de la mec??nica cu??ntica m??s filos??ficos, como la falta de determinista causalidad y la afirmaci??n de que una sola part??cula subat??mica puede ocupar numerosas ??reas de espacio a la vez. Tambi??n fue el primero en notar algunas de las consecuencias aparentemente ex??ticas de enredo y los utiliz?? para formular la Paradoja de Einstein-Podolsky-Rosen, con la esperanza de demostrar que la mec??nica cu??ntica tiene consecuencias inaceptables. Esto fue en 1935, pero en 1964 se demostr?? por John Bell (ver Desigualdad de Bell) esa suposici??n de Einstein de que la mec??nica cu??ntica es correcta, pero tiene que ser completada por variables ocultas, se bas?? en suposiciones filos??ficas err??neas: de acuerdo con el papel de J. Bell y el Interpretaci??n de Copenhague (la interpretaci??n com??n de la mec??nica cu??ntica por los f??sicos durante d??cadas), y contrariamente a las ideas de Einstein, la mec??nica cu??ntica es

ni una teor??a "realista" (ya que las mediciones cu??nticas no declaran propiedades pre-existentes, sino que se preparan propiedades)

ni una teor??a local (esencialmente no, debido a que el vector de estado 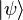$| \ Psi \ rangle$ determina simult??neamente las amplitudes de probabilidad en todos los sitios, $| \ Psi \ rangle \ a \ psi (\ mathbf r), \ forall \ mathbf r$ ).

La paradoja de Einstein-Podolsky-Rosen muestra en todo caso, que existen experimentos por los cuales se puede medir el estado de una part??cula e instant??neamente cambiar el estado de su pareja enredada, aunque las dos part??culas pueden ser una distancia arbitraria aparte; Sin embargo, este efecto no viola causalidad, ya que no hay transferencia de la informaci??n que pasa. Estos experimentos son la base de algunas de las aplicaciones m??s actuales de la teor??a, criptograf??a cu??ntica, que funciona bien, aunque a muy corta distancia de lo general ${\ Le}$ 1000 km de estar en el mercado desde el a??o 2004.

S?? existen teor??as cu??nticas que incorporan ejemplo de la relatividad especial, para, electrodin??mica cu??ntica (QED), que es actualmente la teor??a f??sica probado con mayor precisi??n -y ??stos se sit??an en el coraz??n de la moderna f??sica de part??culas . La gravedad es despreciable en muchas ??reas de la f??sica de part??culas, por lo que la unificaci??n entre la relatividad general y la mec??nica cu??ntica no es un asunto urgente en aquellas aplicaciones. Sin embargo, la falta de una teor??a correcta de la gravedad cu??ntica es un tema importante en la cosmolog??a .

Los intentos de una teor??a unificada

Las inconsistencias se presentan cuando uno trata de unirse a las leyes cu??nticas con la relatividad general , una descripci??n m??s elaborada de espacio-tiempo que incorpora la gravitaci??n . La resoluci??n de estas contradicciones ha sido un objetivo importante del XX - y XXI f??sica -century. Muchos f??sicos prominentes, entre ellos Stephen Hawking , han trabajado en el intento de descubrir un " Gran Unificaci??n Theory "que combina no s??lo diferentes modelos de la f??sica subat??mica, pero tambi??n se deriva cuatro fuerzas del universo-la la fuerza fuerte, electromagnetismo , fuerza d??bil, y la gravedad - desde una ??nica fuerza o fen??meno.

La mec??nica cu??ntica y la f??sica cl??sica

Las predicciones de la mec??nica cu??ntica se han verificado experimentalmente con un muy alto grado de precisi??n. Por lo tanto, la l??gica actual de principio de correspondencia entre la mec??nica cl??sica y cu??ntica es que todos los objetos obedecen las leyes de la mec??nica cu??ntica y la mec??nica cl??sica est?? a la mec??nica cu??ntica de sistemas grandes (o una estad??stica mec??nica cu??ntica de una gran colecci??n de part??culas). Las leyes de la mec??nica cl??sica de este modo se siguen de las leyes de la mec??nica cu??ntica en el l??mite de los sistemas grandes o grandes n??meros cu??nticos.

Principales diferencias entre las teor??as cl??sicas y cu??nticas ya se han mencionado anteriormente en las observaciones sobre la Paradoja de Einstein-Podolsky-Rosen. Esencialmente, la diferencia se reduce a la afirmaci??n de que la mec??nica cu??ntica es coherente (adici??n de amplitudes), mientras que las teor??as cl??sicas son incoherente (adici??n de intensidades). Por lo tanto, las cantidades tales como longitudes de coherencia y tiempos de coherencia entran en juego. Para organismos microsc??picos la extensi??n del sistema es ciertamente mucho m??s peque??o que la longitud de coherencia; para los cuerpos macrosc??picos que uno espera que sea al rev??s.

Esto est?? de acuerdo con las siguientes observaciones:

Muchas de las propiedades macrosc??picas "" de los sistemas "cl??sicos" son consecuencias directas del comportamiento cu??ntico de sus partes. Por ejemplo, la estabilidad de la materia a granel (que consiste en ??tomos y mol??culas que colapsar r??pidamente bajo las fuerzas el??ctricas solo), la rigidez de este asunto, mec??nica, t??rmica, qu??mica, propiedades ??pticas y magn??ticas de este asunto: son todos los resultados de la interacci??n de cargas el??ctricas bajo las reglas de la mec??nica cu??ntica.

Mientras comportamiento aparentemente ex??tico de la materia postulada por la mec??nica cu??ntica y la teor??a de la relatividad a ser m??s evidentes cuando se trata de extremadamente r??pido movimiento o part??culas extremadamente peque??as, las leyes de la f??sica cl??sica "newtoniano" siguen siendo preciso en la predicci??n del comportamiento de los alrededores ("grande") -objetos de la orden del tama??o de las mol??culas grandes y m??s grandes-a velocidades mucho menor que la velocidad de la luz.

Teor??a

Hay numerosas formulaciones matem??ticamente equivalente de la mec??nica cu??ntica. Una de las formulaciones m??s antiguo y m??s utilizado es el teor??a de la transformaci??n propuesta por Cambridge f??sico te??rico Paul Dirac , que unifica y generaliza las dos primeras formulaciones de la mec??nica cu??ntica, mec??nica matricial (inventado por Werner Heisenberg) y la mec??nica ondulatoria (inventado por Erwin Schrodinger).

En esta formulaci??n, el estado instant??neo de un sistema cu??ntico codifica las probabilidades de sus propiedades medibles, o " observables ". Ejemplos de observables incluyen energ??a , posici??n, impulso y momento angular . Observables pueden ser tanto continua (por ejemplo, la posici??n de una part??cula) o discreta (por ejemplo, la energ??a de un electr??n unido a un ??tomo de hidr??geno).

En general, la mec??nica cu??ntica no asigna valores definidos a los observables. En cambio, hace predicciones sobre distribuciones de probabilidad ; es decir, la probabilidad de obtener cada uno de los posibles resultados de la medici??n de un observable. Naturalmente, estas probabilidades depender??n del estado cu??ntico en el instante de la medici??n. Hay, sin embargo, ciertos estados que est??n asociados con un valor definido de un observable particular. Estos son conocidos como "estados propios" de lo observable ("eigen" puede ser m??s o menos traducido del alem??n como inherente o como una caracter??stica). En el mundo cotidiano, es natural e intuitiva de pensar en todo estar en un estado propio de cada observable. Todo parece tener una posici??n definida, un impulso definitivo, y un tiempo definido de ocurrencia. Sin embargo, la mec??nica cu??ntica no se??alan claramente los valores exactos de la posici??n o el impulso de una determinada part??cula en un espacio dado en un tiempo finito; m??s bien, s??lo proporciona una gama de probabilidades de que la part??cula donde podr??a ser. Por lo tanto, se hizo necesario el uso de palabras diferentes para (a) el estado de algo que tiene una relaci??n de incertidumbre y (b) un estado que tiene un valor definido. Este ??ltimo es el llamado "estado propio" de la propiedad que se est?? midiendo.

Por ejemplo, considere un libre de part??culas. En la mec??nica cu??ntica, existe la dualidad onda-part??cula de modo que las propiedades de la part??cula pueden ser descritos como una onda. Por lo tanto, su estado cu??ntico se puede representar como una onda , de forma arbitraria y que se extiende sobre todo el espacio, llamado funci??n de onda. La posici??n y el momento de la part??cula son observables. La Principio de incertidumbre de la mec??nica cu??ntica afirma que tanto la posici??n y el impulso no pueden simult??neamente ser conocidos con precisi??n infinita al mismo tiempo. Sin embargo, se puede medir s??lo la posici??n solo de una part??cula libre en movimiento la creaci??n de un estado propio de la posici??n con una funci??n de onda que es muy grande en una posici??n particular x, y casi cero en todas partes. Si uno realiza una medici??n de la posici??n en una funci??n de onda tal, el resultado x se obtiene con casi el 100% de probabilidad. En otras palabras, casi se conoce la posici??n de la part??cula libre. Esto se llama un estado propio de la posici??n (matem??ticamente m??s preciso: un estado propio generalizada ( eigendistribution)). Si la part??cula est?? en un estado propio de la posici??n entonces su momento es completamente desconocido. Un eigenstate de impulso, por otro lado, tiene la forma de una onda plana. Se puede demostrar que la longitud de onda es igual a h / p, donde h es P constante de Planck es el impulso del estado propio . Si la part??cula est?? en un estado propio del momento, entonces su posici??n es completamente borrosa a cabo.

Por lo general, un sistema no estar?? en un estado propio de lo observable nos interesa. Sin embargo, si se mide el observable, la funci??n de onda ser?? instant??neamente ser un estado propio (o eigenstate generalizada) de ese observable. Este proceso se conoce como colapso funci??n de onda. Se trata de la ampliaci??n del sistema en estudio para incluir el dispositivo de medici??n, por lo que un c??lculo cu??ntico detallada ya no ser??a viable y una descripci??n cl??sica debe ser utilizado. Si se conoce la funci??n de onda correspondiente en el instante antes de la medici??n, uno ser?? capaz de calcular la probabilidad de colapso en cada uno de los posibles estados propios. Por ejemplo, la part??cula libre en el ejemplo anterior por lo general tienen una funci??n de onda que es un paquete de ondas centrado alrededor de alguna posici??n x _0, ni un estado propio de posici??n ni de impulso significa. Cuando se mide la posici??n de la part??cula, es imposible predecir con certeza el resultado de que obtendremos. Es probable, pero no seguro, que ser?? cerca de x _0, donde la amplitud de la funci??n de onda es grande. Despu??s se realiza la medici??n, habiendo obtenido alg??n resultado x, la funci??n de onda colapsa en un estado propio posici??n centrada en x.

Las funciones de onda pueden cambiar a medida que pasa el tiempo. Una ecuaci??n conocida como la Ecuaci??n de Schr??dinger describe c??mo las funciones de onda cambian en el tiempo, un papel similar al de la segunda ley de Newton en la mec??nica cl??sica. La ecuaci??n de Schr??dinger, aplicado al ejemplo antes mencionado de la part??cula libre, predice que el centro de un paquete de ondas se mover?? a trav??s del espacio a una velocidad constante, como una part??cula cl??sica con no hay fuerzas que act??an sobre ella. Sin embargo, el paquete de ondas tambi??n se extender?? como el tiempo progresa, lo que significa que la posici??n se vuelve m??s incierta. Esto tambi??n tiene el efecto de convertir los estados propios de posici??n (que puede ser pensado de paquetes de ondas como infinitamente afilados) en paquetes de onda ampliado que no son estados propios de posici??n m??s largos.

Algunas funciones de onda producen distribuciones de probabilidad que son constantes en el tiempo. Muchos de los sistemas que son tratados de forma din??mica en la mec??nica cl??sica son descritos por dichas funciones de onda "est??ticos". Por ejemplo, un solo electr??n excitado en un ??tomo se representa cl??sicamente como una part??cula que se mueve en una trayectoria circular alrededor del n??cleo at??mico , mientras que en la mec??nica cu??ntica que se describe mediante una est??tica, esf??ricamente sim??trica funci??n de onda que rodea el n??cleo ( Fig. 1 ). (Tenga en cuenta que s??lo los m??s bajos estados de momento angular, s etiquetados, son esf??ricamente sim??trica).

La evoluci??n temporal de las funciones de onda es determinista en el sentido de que, dada una funci??n de onda en un momento inicial, se hace una predicci??n definida de lo que ser?? la funci??n de onda en cualquier momento posterior. Durante una medici??n, el cambio de la funci??n de onda en otra no es determinista, sino m??s bien impredecible, es decir, azar.

El probabil??stico naturaleza de la mec??nica cu??ntica as?? surge del acto de medici??n. Este es uno de los aspectos m??s dif??ciles de sistemas cu??nticos de entender. Fue el tema central en la famosa Bohr-Einstein debates, en los que los dos cient??ficos intentaron aclarar estos principios fundamentales por medio de experimentos mentales. En las d??cadas posteriores a la formulaci??n de la mec??nica cu??ntica, la cuesti??n de lo que constituye una "medida" ha sido ampliamente estudiado. Las interpretaciones de la mec??nica cu??ntica se han formulado para acabar con el concepto de "colapso funci??n de onda"; v??ase, por ejemplo, el interpretaci??n estado relativo. La idea b??sica es que cuando un sistema cu??ntico interact??a con un aparato de medici??n, se convierten en sus respectivas funciones de onda enredado, por lo que el sistema cu??ntico original, deja de existir como una entidad independiente. Para m??s detalles, ver el art??culo sobre medici??n de la mec??nica cu??ntica.

Formulaci??n matem??tica

En la formulaci??n matem??tica rigurosa de la mec??nica cu??ntica, desarrollada por Paul Dirac y John von Neumann , los posibles estados de un sistema mec??nico cu??ntico est??n representados por vectores unitarios (llamados "vectores de estado") que residen en un complejo separable Espacio de Hilbert (diversamente llamado el "espacio de estado" o el "espacio de Hilbert asociado" del sistema) bien definido hasta un n??mero complejo de norma 1 (el factor de fase). En otras palabras, los estados posibles son puntos en el projectivization de un espacio de Hilbert. La naturaleza exacta de este espacio de Hilbert es dependiente del sistema; por ejemplo, el espacio de estados para la posici??n y el momento los estados es el espacio de funciones integrables cuadrados, mientras que el espacio de estados para el giro de un solo prot??n es s??lo el producto de dos planos complejos. Cada observable est?? representado por un maximally- Herm??tica (precisamente: por un autoadjunto) lineal operador que act??a sobre el espacio de estados. Cada eigenstate de un observables corresponde a un vector propio del operador, y el correspondiente valor propio corresponde al valor de la observable en ese estado propio. Si el espectro del operador es discreto, el observable s??lo puede alcanzar esos valores propios discretos.

La evoluci??n temporal de un estado cu??ntico es descrito por el Ecuaci??n de Schr??dinger, en el que la Hamilton, el operador correspondiente a la energ??a total del sistema, genera evoluci??n en el tiempo.

La producto interno entre dos vectores de estado es un n??mero complejo conocido como amplitud de probabilidad. Durante una medici??n, la probabilidad de que un sistema se colapsa desde un estado inicial dado a un eigenstate particular es dada por el cuadrado de la valor absoluto de las amplitudes de probabilidad entre los estados inicial y final. Los posibles resultados de una medici??n son los valores propios del operador - lo que explica la elecci??n de hermitianos, para que todos los valores propios son reales. Podemos encontrar la distribuci??n de probabilidad de un observable en un estado dado computando el descomposici??n espectral del operador correspondiente. Heisenberg principio de incertidumbre est?? representada por la afirmaci??n de que los operadores correspondientes a ciertos observables no lo hacen conmute.

La ecuaci??n de Schr??dinger act??a en toda la amplitud de probabilidad, no s??lo su valor absoluto. Considerando que el valor absoluto de la amplitud de probabilidad codifica la informaci??n acerca de las probabilidades, su fase codifica la informaci??n acerca de la interferencia entre estados cu??nticos. Esto da lugar al comportamiento de onda de estados cu??nticos.

Resulta que las soluciones anal??ticas de la ecuaci??n de Schr??dinger s??lo est??n disponibles para un peque??o n??mero de modelo hamiltonianos, de los cuales el oscilador arm??nico cu??ntico, la part??cula en una caja, la ion hidr??geno molecular y la ??tomo de hidr??geno son los representantes m??s importantes. Incluso el helio ??tomo, que contiene s??lo un electr??n m??s que el hidr??geno, desaf??a todos los intentos de un tratamiento totalmente anal??tica. Existen varias t??cnicas para generar soluciones aproximadas. Por ejemplo, en el m??todo conocido como teor??a de las perturbaciones uno utiliza los resultados anal??ticos para un modelo de la mec??nica cu??ntica sencilla de generar resultados de un modelo m??s complicado relacionado con el modelo simple, por ejemplo, la adici??n de un d??bil energ??a potencial. Otro m??todo es la "ecuaci??n semi-cl??sica del movimiento" enfoque, que se aplica a los sistemas para los que la mec??nica cu??ntica produce desviaciones d??biles del comportamiento cl??sico. Las desviaciones se pueden calcular en base al movimiento cl??sico. Este enfoque es importante para el campo de la caos cu??ntico.

Una formulaci??n alternativa de la mec??nica cu??ntica es Feynman 's Integral de caminos, en el que una amplitud de la mec??nica cu??ntica es considerado como una suma de historias entre los estados inicial y final; esta es la contraparte de la mec??nica cu??ntica de principios de actuaci??n en la mec??nica cl??sica.

Interacciones con otras teor??as cient??ficas

Las reglas fundamentales de la mec??nica cu??ntica son muy amplias. Afirman que el espacio de estados de un sistema es una Espacio de Hilbert y los observables son Hermitianos actuando en ese espacio, pero no nos dicen que los operadores del espacio de Hilbert o que, o si es que existe. Estos deben ser elegidos adecuadamente con el fin de obtener una descripci??n cuantitativa de un sistema cu??ntico. Una gu??a importante para tomar estas decisiones es la principio de correspondencia, que establece que las predicciones de la mec??nica cu??ntica se reducen a las de la f??sica cl??sica, cuando un sistema se mueve a altas energ??as o equivalentemente, n??meros cu??nticos grandes. En otras palabras, la mec??nica cl??sica es simplemente una mec??nica cu??ntica de sistemas grandes. Este l??mite "alta energ??a" se conoce como el l??mite cl??sico o su correspondencia. Por consiguiente, puede comenzar a partir de un modelo cl??sico establecida de un sistema particular, y tratar de adivinar el modelo cu??ntico subyacente que da lugar al modelo cl??sico en el l??mite de la correspondencia

Lista de los problemas sin resolver en la f??sica
En el l??mite de la correspondencia de la mec??nica cu??ntica:* ??Existe una interpretaci??n preferida de la mec??nica cu??ntica?* ??C??mo funciona la descripci??n cu??ntica de la realidad, que incluye elementos tales como la superposici??n de estados y colapso funci??n de onda, da lugar a la realidad que percibir?

Cuando la mec??nica cu??ntica se redact?? inicialmente, se aplica a los modelos cuyo l??mite correspondencia era no relativistas mec??nica cl??sica . Por ejemplo, el modelo de la bien conocida la oscilador arm??nico cu??ntico utiliza una expresi??n expl??cita no relativista para la energ??a cin??tica del oscilador, y es por lo tanto una versi??n cu??ntica de la oscilador arm??nico cl??sico.

Los primeros intentos para fusionar la mec??nica cu??ntica con la relatividad especial implicaron la sustituci??n de la ecuaci??n de Schr??dinger con una ecuaci??n como la covariante Ecuaci??n de Klein-Gordon o la Ecuaci??n de Dirac. Si bien estas teor??as tuvieron ??xito en la explicaci??n de muchos resultados experimentales, ten??an ciertas cualidades insatisfactorias derivadas de su abandono de la creaci??n relativista y la aniquilaci??n de part??culas. Una teor??a cu??ntica relativista completamente necesario el desarrollo de la teor??a cu??ntica de campos , que se aplica cuantizaci??n a un campo en lugar de un conjunto fijo de part??culas. La primera teor??a cu??ntica de campos completos, electrodin??mica cu??ntica, proporciona una descripci??n completamente cu??ntica de la interacci??n electromagn??tica .

El aparato completo de la teor??a cu??ntica de campos es a menudo innecesario para describir sistemas electrodin??micos. Un enfoque m??s sencillo, un empleado desde el inicio de la mec??nica cu??ntica, es tratar cargadas part??culas como objetos de la mec??nica cu??ntica que se act??a por un campo electromagn??tico cl??sico. Por ejemplo, el modelo cu??ntico elemental de la ??tomo de hidr??geno describe el campo el??ctrico de la ??tomo de hidr??geno usando un cl??sica $- \ Frac {e ^ 2} {4 \ pi \ \ epsilon_0 \} \ frac {1} {r}$ Potencial de Coulomb. Este enfoque de "semi-cl??sica" falla si las fluctuaciones cu??nticas en el campo electromagn??tico juegan un papel importante, como en la emisi??n de fotones por part??culas cargadas.

Teor??as cu??nticas de campos para la fuerza nuclear fuerte y la fuerza nuclear d??bil se han desarrollado. La teor??a cu??ntica de campos de la fuerza nuclear fuerte se llama cromodin??mica cu??ntica, y describe las interacciones de las part??culas subnucleares: quarks y gluones. La d??bil fuerza nuclear y la fuerza electromagn??tica se unificaron, en sus formas cuantificados, en una sola teor??a del campo cu??ntico conocido como teor??a electrod??bil.

Se ha demostrado que es dif??cil construir modelos cu??nticos de la gravedad , el restante fuerza fundamental. Aproximaciones semi-cl??sicos son viables, y han dado lugar a predicciones, como la radiaci??n de Hawking . Sin embargo, la formulaci??n de una teor??a completa de la la gravedad cu??ntica se ve obstaculizada por las aparentes incompatibilidades entre la relatividad general , la teor??a m??s precisa de la gravedad actualmente conocida, y algunos de los supuestos fundamentales de la teor??a cu??ntica. La resoluci??n de estas incompatibilidades es un ??rea de investigaci??n activa, y las teor??as, como la teor??a de cuerdas son algunos de los posibles candidatos para una futura teor??a de la gravedad cu??ntica.

Derivaci??n de cuantizaci??n

La part??cula en una caja de energ??a potencial 1-dimensional es el m??s simple ejemplo en el que las restricciones conducen a la cuantizaci??n de los niveles de energ??a. La caja se define como cero potencial de energ??a dentro de un cierto intervalo e infinito en todas partes fuera de ese intervalo. Para el caso 1-dimensional en el 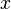$x$ direcci??n, la ecuaci??n de Schr??dinger independiente del tiempo puede escribirse como:

$- \ Frac {\ hbar ^ 2} {2m} \ frac {d ^ 2 \ psi} {dx ^ 2} = E \ psi.$

Las soluciones generales son:

$\ Psi = A e ^ {ikx} + B e ^ {- ikx} \; \; \; \; \; \; E = \ frac {k ^ 2 \ hbar ^ 2} {2m}$

$\ Psi = C \ sin kx + D \ cos kx \;$ ( reescritura exponencial)

La presencia de las paredes de la caja restringe las soluciones aceptables para la funci??n de onda. En cada pared:

$\ Psi = 0 \; \ Mathrm {en} \; \; x = 0, \; x = L$

Considere x = 0

sen 0 = 0, cos 0 = 1. Para satisfacer $\ Psi = 0 \;$ D = 0 (cos se retira plazo)

Ahora Considere lo siguiente: $\ Psi = C \ sen kx \;$

en X = L, $\ Psi = C \ sin kL \;$
Si C = 0, $\ Psi = 0 \;$ para todo x, y entrar??a en conflicto con la interpretaci??n de Born
Por lo tanto, el pecado kL debe ser satisfecha por

$kL = n \ pi \; \; \; \; n = 1,2,3,4,5 \;$

En esta situaci??n, n debe ser un entero que muestra la cuantificaci??n de los niveles de energ??a.

Aplicaciones

La mec??nica cu??ntica ha tenido un enorme ??xito en la explicaci??n de muchas de las caracter??sticas de nuestro mundo. El comportamiento individual de las part??culas subat??micas que componen todas las formas de la materia - los electrones , protones , neutrones , fotones y otros-a menudo s??lo puede ser descrito de manera satisfactoria mediante la mec??nica cu??ntica. La mec??nica cu??ntica ha influido fuertemente en la teor??a de cuerdas , un candidato para un teor??a del todo (ver reduccionismo). Tambi??n est?? relacionado con la mec??nica estad??stica .

La mec??nica cu??ntica es importante para la comprensi??n de c??mo los ??tomos individuales se combinan de forma covalente para formar sustancias qu??micas o mol??culas. La aplicaci??n de la mec??nica cu??ntica a la qu??mica se conoce como qu??mica cu??ntica . Mec??nica (relativista) cu??nticos pueden en principio describir matem??ticamente la mayor parte de la qu??mica. La mec??nica cu??ntica pueden proporcionar informaci??n cuantitativa en los procesos de enlace i??nico y covalente, mostrando expl??citamente qu?? mol??culas son energ??ticamente favorable para que los dem??s, y en aproximadamente cu??nto. La mayor??a de los c??lculos realizados en qu??mica computacional se basan en la mec??nica cu??ntica.

Gran parte de la moderna tecnolog??a opera a una escala donde los efectos cu??nticos son significativos. Los ejemplos incluyen el l??ser , la transistor, la microscopio electr??nico, y imagen de resonancia magn??tica. El estudio de los semiconductores condujo a la invenci??n de la diodo y la transistor, que son indispensables para los modernos productos electr??nicos .

Actualmente, los investigadores est??n buscando m??todos robustos de la manipulaci??n directa de estados cu??nticos. Se est??n realizando esfuerzos para desarrollar criptograf??a cu??ntica, que permitir?? garantizar la transmisi??n segura de informaci??n . Un objetivo m??s lejano es el desarrollo de ordenadores cu??nticos , que se espera para realizar ciertas tareas computacionales exponencialmente m??s r??pido que los cl??sicos ordenadores . Otro tema de investigaci??n activa es teleportaci??n cu??ntica, que trata de t??cnicas para transmitir estados cu??nticos en distancias arbitrarias.

En muchos dispositivos, incluso el simple interruptor de la luz, t??nel cu??ntico es vital, ya que de lo contrario los electrones de la corriente el??ctrica no pod??an penetrar la barrera de potencial formado por, en el caso del interruptor de la luz, de una capa de ??xido. Chips de memoria flash encuentran en Unidades USB tambi??n utilizan t??nel cu??ntico borrar sus c??lulas de memoria.

Consecuencias filos??ficas

Desde su creaci??n, los muchos resultados contra-intuitiva de la mec??nica cu??ntica han provocado fuerte filos??fico debate y muchos interpretaciones. Incluso cuestiones fundamentales como Normas b??sicas de Max Born relativos amplitudes de probabilidad y distribuciones de probabilidad tomaron d??cadas para ser apreciado.

La Interpretaci??n de Copenhague, en gran parte debido al f??sico te??rico dan??s Niels Bohr , es la interpretaci??n de la mec??nica cu??ntica de mayor aceptaci??n entre los f??sicos. Seg??n ??l, la naturaleza probabil??stica de la mec??nica cu??ntica predicciones no se puede explicar en t??rminos de alguna otra teor??a determinista, y no simplemente reflejan nuestro conocimiento limitado.La mecánica cuántica proporcionaprobabilísticosresultados debido a que el universo físico es en sí probabilístico y nodeterminista.

Albert Einstein no le gustaba esta pérdida de determinismo en la medición. (De ahí su famosa frase "Dios no juega a los dados con el universo".) Él sostuvo que no debería haber una teoría variable de la mecánica cuántica locales subyacente ocultos y en consecuencia la actual teoría era incompleta. En represalia del dogma religioso aparentemente se produjo una serie de objeciones a la teoría, el más famoso de los cuales se ha conocido como la paradoja EPR. Existen sospechas de que la mecánica cuántica fue creado para ser confuso y difícil de refutar con el fin de dar a los científicos menores la oportunidad de pasar a la historia junto a Einstein. John Bell demostró que la paradoja EPR llevó a comprobables experimentalmente diferencias entre la mecánica cuántica y las teorías locales. Los experimentos cuyos vigencias son altamente cuestionado se han tomado como una confirmación de que la mecánica cuántica es correcta y el mundo real debe ser descrito en términos de teorías no locales.

El escritor CS Lewis visto la mecánica cuántica como incompleta, debido a las nociones de indeterminismo no estaban de acuerdo con sus creencias religiosas. Lewis, profesor de Inglés, era de la opinión de que el principio de incertidumbre de Heisenberg era más una limitación epistémica que una indicación de indeterminación ontológica, y en este sentido se cree de manera similar a muchos defensores de las variables ocultas teorías. La Bohr-Einstein debates proporcionar una vibrante crítica de la interpretación de Copenhague desde el punto de vista epistemológico.

La Everett universos paralelos, formulado en 1956, sostiene que todas las posibilidades descritas por la teoría cuántica se producen simultáneamente en un " multiverso ", compuesto de universos paralelos en su mayoría independientes. Esto no se logra mediante la introducción de un nuevo axioma de la mecánica cuántica, sino por el contrario por eliminar el axioma del colapso del paquete de ondas: Todos los posibles estados coherentes del sistema de medida y los aparatos de medición (incluyendo el observador) están presentes en una verdadera física (no sólo formalmente matemática, como en otras interpretaciones) superposición cuántica. (Tal superposición de combinaciones estatales consistentes de diferentes sistemas se llama un estado entrelazado.) Mientras que el multiverso es determinista, percibimos el comportamiento no determinista regido por probabilidades, ya que podemos observar solamente el universo, es decir, el aporte estatal coherente a la mencionada superposición, que habitamos. La interpretación de Everett es perfectamente coherente con los experimentos de John Bell y los hace intuitivamente comprensible. Sin embargo, de acuerdo con la teoría de la decoherencia cuántica, los universos paralelos nunca será accesible para nosotros. Esta falta de acceso puede entenderse de la siguiente manera: una vez que se realiza una medición, el sistema de medición se vuelve enredado tanto con el físico que mide y un gran número de otras partículas, algunas de las cuales son fotones que vuelan lejos hacia el otro extremo del universo; con el fin de demostrar que la función de onda no se derrumbó uno tendría que llevar todas estas partículas hacia atrás y medir de nuevo, junto con el sistema que se midió originalmente. Esto es completamente impracticable, pero incluso si uno puede hacer teóricamente esto, sería destruir cualquier evidencia de que la medida original tuvo lugar (incluyendo la memoria del físico).

Recuperado de " http://en.wikipedia.org/w/index.php?title=Quantum_mechanics&oldid=230232047 "