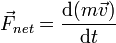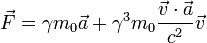Leyes de Newton

Primera y segunda ley de Newton, en Am??rica, desde la edici??n original 1687 de la Principia Mathematica.

Leyes del movimiento de Newton son tres leyes f??sicas que proporcionan relaciones entre las fuerzas que act??an sobre una cuerpo y el movimiento del cuerpo. Ellos fueron compilados por primera vez por Sir Isaac Newton en su obra Philosophiae Naturalis Principia Mathematica ( 1687). Las leyes son la base de la mec??nica cl??sica y el propio Newton ellos utilizan para explicar muchos resultados relativos al movimiento de los objetos f??sicos. En el tercer volumen del texto, Newton mostr?? que estas leyes del movimiento, junto con su la ley de la gravitaci??n universal, explica las leyes de Kepler del movimiento planetario .

Breves declaraciones tradicionales de las tres leyes:

1. Un cuerpo f??sico permanecer?? en reposo o continuar?? movi??ndose a una velocidad constante de velocidad , a menos que fuera fuerza neta act??a sobre ??l.
2. La fuerza neta sobre un cuerpo es igual a su masa multiplicada por su aceleraci??n .
3. Para cada acci??n hay una reacci??n igual y opuesta.

Las tres leyes en detalle

Leyes de Newton describen la aceleraci??n de masivas part??culas. En lenguaje moderno, las leyes pueden enunciarse como:

Primera ley

Si ninguna red de fuerza act??a sobre una part??cula, entonces es posible seleccionar un conjunto de marcos de referencia, llamados marcos de referencia inerciales, observados desde la que la part??cula se mueve sin ning??n cambio en la velocidad . Esta ley a menudo se simplifica en la frase "Un objeto permanecer?? en reposo o continuar a una velocidad constante a menos que act??e sobre ??l una fuerza de desequilibrio exterior".

Segunda ley

Observado desde un sistema de referencia inercial, la fuerza neta sobre una part??cula es proporcional a la tasa de tiempo de cambio lineal de su impulso : . Momentum es el producto de la masa y la velocidad. Cuando la masa es constante, esta ley se afirma a menudo como 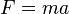(La fuerza neta sobre un objeto es igual a la masa del objeto multiplicada por su aceleraci??n).

Tercera ley

Siempre que una part??cula A ejerce una fuerza sobre otra part??cula B, B ejerce simult??neamente una fuerza sobre A con la misma magnitud en la direcci??n opuesta. La forma fuerte de la ley postula adem??s que estas dos fuerzas act??an a lo largo de la misma l??nea. Esta ley a menudo se simplifica en la frase "Cada acci??n tiene una reacci??n igual y opuesta".

En los medios de interpretaci??n, la aceleraci??n, y, lo m??s importante, la fuerza se supone que son cantidades definidas externamente. Esta es la la ??nica interpretaci??n m??s com??n, pero no: se puede considerar que las leyes son una definici??n de estas cantidades. Observe que la segunda ley s??lo se mantiene cuando la observaci??n se hace a partir de un sistema de referencia inercial, y desde un sistema de referencia inercial est?? definida por la primera ley, pedir una prueba de la primera ley de la segunda ley es una falacia l??gica.

La primera ley de Newton: ley de la inercia

Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter en directum, nisi quatenus un viribus impressis cogitur STATUM illum mutare.

Todo cuerpo persevera en su estado de estar en reposo o de movimiento uniforme en l??nea recta, salvo en lo que se ve obligado a cambiar su estado por la fuerza impresionado.

Esta ley tambi??n se conoce como la ley de inercia.

Esto a menudo se parafrasea como "fuerza neta cero implica una aceleraci??n de cero", pero esto es una simplificaci??n excesiva. Como formulada por Newton, la primera ley es m??s que un caso especial de la segunda ley. Newton arregl?? sus leyes en orden jer??rquico por una buena raz??n (por ejemplo, v??ase Gailili y Tseitlin 2003). En esencia, la primera ley establece marcos de referencia para que los dem??s leyes aplicables, estos marcos se denominan sistemas inerciales. Para entender por qu?? esto es necesario, considere una bola en reposo dentro de un cuerpo de aceleraci??n: un avi??n en una pista ser?? suficiente para este ejemplo. Desde la perspectiva de cualquier persona dentro del avi??n (es decir, desde el marco de la aeronave de referencia cuando se ponen en t??rminos t??cnicos) la pelota se parecen moverse hacia atr??s cuando el avi??n acelera hacia adelante (la misma sensaci??n de ser empujado de nuevo en su asiento mientras el avi??n acelera). Esto parece contradecir la segunda ley de Newton como, desde el punto de vista de los pasajeros, no parece haber ninguna fuerza que act??a sobre la pelota que podr??a causar que se mueva. La raz??n por la que es, de hecho, no hay contradicci??n se debe a que la segunda ley de Newton (sin excepciones) no es aplicable en esta situaci??n porque la primera ley de Newton no era aplicable en esta situaci??n (es decir, la pelota estacionaria no permanece estacionaria). Por lo tanto, es importante establecer si las distintas leyes son aplicables o no, ya que no son aplicables en todas las situaciones. En un plano m??s t??cnico, aunque las leyes de Newton no son aplicables en los marcos no inerciales de referencia, como el avi??n acelera, que se pueden hacer para hacerlo con la introducci??n de un " fuerza ficticia "que act??a sobre todo el sistema: b??sicamente, mediante la introducci??n de una fuerza que cuantifica el movimiento an??malo de objetos dentro de ese sistema (tal como el bal??n en movimiento sin una influencia evidente en el ejemplo anterior).

La fuerza neta sobre un objeto es la suma vectorial de todas las fuerzas que act??an sobre el objeto. La primera ley de Newton dice que si esta suma es cero, el estado de movimiento del objeto no cambia. En esencia, se hace que los dos puntos siguientes:

• Un objeto que no se mueve, no se mover?? hasta que una fuerza neta act??a sobre ??l.

• Un objeto que est?? en movimiento no cambiar?? su velocidad (aceleraci??n) hasta que una fuerza neta act??a sobre ??l.

El primer punto parece relativamente obvia para la mayor??a de la gente, pero el segundo puede tomar alg??n pensamiento a trav??s, porque no tenemos experiencia en la vida cotidiana de las cosas que mantenerse en movimiento para siempre (excepto los cuerpos celestes). Si uno se desliza un disco de hockey lo largo de una mesa, que no se mueve por siempre, se ralentiza y, finalmente, llega a una parada. Pero de acuerdo con las leyes de Newton, esto es debido a una fuerza est?? actuando sobre el disco de hockey y, por supuesto, no hay fuerza de fricci??n entre la mesa y el disco, y que la fuerza de fricci??n es en la direcci??n opuesta del movimiento. Es esta fuerza la que hace que el objeto de frenar hasta detenerse. En ausencia de tal fuerza, como la aproximaci??n que realiza una mesa de hockey de aire o pista de hielo, el movimiento del disco no lo har??a lento. La primera ley de Newton es s??lo una reafirmaci??n de lo que Galileo ya hab??a descrito y Newton dio cr??dito a Galileo. Se diferencia de la idea de Arist??teles de que todos los objetos tienen un lugar natural en el universo. Arist??teles cre??a que los objetos pesados como rocas quer??an estar en reposo en la Tierra y que los objetos ligeros como el humo quer??an estar en reposo en el cielo y las estrellas quer??an permanecer en los cielos.

Sin embargo, una diferencia clave entre la idea de Galileo y Arist??teles es que Galileo se dio cuenta de que la fuerza que act??a sobre un cuerpo determina la aceleraci??n, no la velocidad. Esta idea conduce a la Primera Ley-ninguna fuerza de Newton significa que no hay aceleraci??n, y por lo tanto el cuerpo va a mantener su velocidad.

La Ley de la Inercia aparentemente ocurri?? a varios fil??sofos naturales diferentes y cient??ficos de forma independiente. La inercia del movimiento fue descrito en el siglo tercero antes de Cristo por el fil??sofo chino Mo Tzu, y en el siglo 11 por el Cient??ficos musulmanes, Alhazen y Avicena. El fil??sofo del siglo 17 Ren?? Descartes tambi??n formul?? la ley, a pesar de que no ha realizado ning??n tipo de experimentos para confirmarlo.

No hay manifestaciones perfectas de la ley, como fricci??n generalmente causa una fuerza que act??a sobre un cuerpo en movimiento, e incluso en el espacio ultraterrestre gravitacional fuerzas acto y no puede estar blindados contra, pero la ley sirve para enfatizar las causas primarias de los cambios de estado de un objeto de movimiento:

La segunda ley de Newton: ley de la aceleraci??n

Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.

La velocidad de cambio de impulso de un cuerpo es proporcional a la fuerza resultante que act??a sobre el cuerpo y es en la misma direcci??n.

En 1729 la traducci??n de Motte (del lat??n de Newton), la segunda ley del movimiento lee:

LEY II: La alteraci??n de movimiento es siempre proporcional a la fuerza motriz impresionado; y est?? hecha en la direcci??n de la l??nea derecha en la que esa fuerza est?? impresionado. - Si una fuerza genera un movimiento, una fuerza doble generar?? el doble del movimiento, una fuerza de triple triple del movimiento, ya sea que la fuerza se impresion?? por completo y al mismo tiempo, o en forma gradual y sucesivamente. Y este movimiento (siendo dirige siempre de la misma manera con la fuerza generadora), si el cuerpo se mov??a antes, se suma o se resta del antiguo movimiento, seg??n cuanto conspiran directamente con o son directamente contrarias entre s??; u oblicuamente unido, cuando son oblicuos, a fin de producir un nuevo movimiento compuesto de la determinaci??n de ambos.

Utilizando la notaci??n simb??lica moderna, la segunda ley de Newton se puede escribir como un vector ecuaci??n diferencial :

donde:

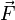es la fuerza de vector

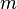es la masa

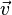es la velocidad del vector

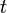es el tiempo .

El producto de la masa y la velocidad es el impulso del objeto (que el propio Newton llama "cantidad de movimiento"). El uso de expresiones algebraicas se hizo popular durante el siglo 18, despu??s de la muerte de Newton, en tanto que la notaci??n vectorial se remonta a finales del siglo 19. El Principia expresa teoremas matem??ticos en palabras y utiliza constantemente geom??trica en lugar de pruebas algebraicas.

Si la masa del objeto en cuesti??n es constante esta ecuaci??n diferencial se puede reescribir como:

donde:

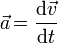es la aceleraci??n .

Un equivalente verbal de esto es "la aceleraci??n de un objeto es proporcional a la fuerza aplicada, e inversamente proporcional a la masa del objeto". Si el impulso var??a de forma no lineal con la velocidad (como hace para altas velocidades-ver la relatividad especial ), a continuaci??n, esta ??ltima versi??n no es exacta.

Tomando la relatividad especial en la consideraci??n, la ecuaci??n se convierte

donde:

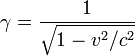
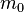es la masa en reposo o masa invariante.

es la velocidad de la luz.

Tenga en cuenta que la fuerza depende de la velocidad del cuerpo en movimiento, la aceleraci??n, y su masa en reposo. Sin embargo, cuando la velocidad del cuerpo en movimiento es mucho menor que la velocidad de la luz, la ecuaci??n anterior se reduce a lo familiar .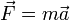

Misa siempre debe ser tomado como constante en la mec??nica cl??sica. Los llamados sistemas de masa variables como un cohete no pueden ser tratados directamente por hacer masa en funci??n del tiempo en la segunda ley. El razonamiento, dada en Introducci??n a la Mec??nica de Kleppner y Kolenkow y otros textos modernos, es un extracto aqu??:

La segunda ley de Newton se aplica fundamentalmente a las part??culas. En la mec??nica cl??sica, las part??culas, por definici??n, tienen una masa constante. En caso de sistemas bien definidos de part??culas, la ley de Newton se puede ampliar mediante la integraci??n sobre todas las part??culas en el sistema. En este caso, tenemos que hacer referencia a todos los vectores del centro de masa. Aplicando la segunda ley para objetos extendidos asume impl??citamente el objeto a ser una colecci??n bien definida de part??culas. Sin embargo, los sistemas de los medios de la variable "como un cohete o un cubo con fugas no consisten en un determinado n??mero de part??culas. Ellos no son sistemas bien definidos. Por lo tanto la segunda ley de Newton no se puede aplicar directamente a ellos. La aplicaci??n ingenua de F = dp / dt dar?? lugar generalmente respuestas incorrectas en estos casos. Sin embargo, la aplicaci??n de la conservaci??n del momento a un sistema completo (como un cohete y el combustible, o un cubo y perd??a agua) dar?? respuestas correctas sin ambig??edades.

Ley de Newton tercero: ley de acciones rec??procas

Lex III: Actioni contrariam semper et ??qualem esse reactionem: sive corporum Duorum actiones in se Mutuo semper esse aequales et in contradictorios contrarias dirigi.

Todas las fuerzas se producen en pares, y estas dos fuerzas son iguales en magnitud y opuestas en direcci??n.

Esta ley de movimiento se parafrasea com??nmente como: "Por cada fuerza hay un igual, pero opuesta, la fuerza".

La tercera ley de Newton. Las fuerzas de los patinadores en cada otra son iguales en magnitud, y en direcciones opuestas

Una traducci??n m??s directa es:

LEY III: Para cada acci??n hay siempre se opone una reacci??n igual: o las acciones mutuas de dos cuerpos entre s?? son siempre iguales, y dirigi?? a las partes contrarias. - Lo que atrae o presiona otra es lo m??s atra??dos o presionados por ese otro. Si pulsa una piedra con el dedo, el dedo tambi??n es presionado por la piedra. Si un caballo dibuja una piedra atada a una cuerda, el caballo (si se me permite decirlo) se dibujar?? igualmente hacia la piedra, porque la cuerda distendido, por el mismo esfuerzo para relajarse o enderece s??, atraer?? a caballo como mucho hacia la piedra, como lo hace la piedra hacia el caballo, y obstruir?? el progreso de la una como mucho a medida que avanza la de la otra. Si un cuerpo incide sobre otro, y por su fuerza de cambiar el movimiento de la otra, que el cuerpo tambi??n (debido a la igualdad de la presi??n mutua) se someter?? a un cambio igual, en su oficio, hacia la parte contraria. Los cambios realizados por estas acciones son iguales, no en las velocidades pero en los movimientos de los cuerpos; es decir, si los cuerpos no se vean obstaculizados por otros impedimentos. Porque, como los movimientos se cambian por igual, los cambios de las velocidades hechas hacia partes contrarias son inversamente proporcionales a los cuerpos. Esta ley tiene lugar tambi??n en lugares de inter??s, como se demostrar?? en el pr??ximo escolio.

En lo anterior, como de costumbre, el movimiento es el nombre de Newton para el momento, por lo tanto, su cuidadosa distinci??n entre el movimiento y la velocidad.

Como se muestra en la figura de la derecha, las fuerzas de los patinadores en cada otra son iguales en magnitud y opuestas en direcci??n. Aunque las fuerzas son iguales, las aceleraciones no son: el patinador menos masivo tendr?? una mayor aceleraci??n de la segunda ley de Newton. Es importante tener en cuenta que el par acto de acci??n / reacci??n en diferentes objetos y no se anulan entre s??. Las dos fuerzas en la tercera ley de Newton son del mismo tipo, por ejemplo, si el camino ejerce una fuerza de fricci??n hacia adelante sobre los neum??ticos de un autom??vil de aceleraci??n, entonces tambi??n es una fuerza de fricci??n que la tercera ley de Newton predice para los neum??ticos de empuje hacia atr??s en la carretera.

Newton utiliz?? la tercera ley para derivar la ley de conservaci??n del momento ; Sin embargo, desde una perspectiva m??s profunda, la conservaci??n del momento es la idea m??s fundamental (derivada a trav??s de El teorema de Noether de Invariancia galileana), y sostiene en los casos en que la tercera ley de Newton parece fallar, por ejemplo, cuando campos de fuerza, as?? como part??culas llevan impulso, y en la mec??nica cu??ntica .

Importancia y rango de validez

Las leyes de Newton fueron verificadas por la experimentaci??n y la observaci??n de m??s de 200 a??os, y son excelentes aproximaciones en las escalas y velocidades de la vida cotidiana. Las leyes del movimiento de Newton, junto con su ley de la gravitaci??n universal y las t??cnicas matem??ticas de c??lculo , siempre que por primera vez una explicaci??n cuantitativa unificada para una amplia gama de fen??menos f??sicos.

Estas tres leyes sostienen que una buena aproximaci??n para objetos macrosc??picos en condiciones cotidianas. Sin embargo, las leyes de Newton (combinar con la Gravitaci??n Universal y Electrodin??mica cl??sica) no son apropiados para su uso en determinadas circunstancias, sobre todo en escalas muy peque??as, muy altas velocidades (en la relatividad especial , la Factor de Lorentz se debe incluir en la expresi??n de impulso junto con masa en reposo y la velocidad) o muy fuertes campos gravitatorios. Por lo tanto, las leyes no se pueden utilizar para explicar fen??menos tales como la conducci??n de la electricidad en un semiconductor , propiedades ??pticas de sustancias, los errores en no-relativista corregidos Los sistemas GPS y la superconductividad . Explicaci??n de estos fen??menos requiere la teor??a f??sica m??s sofisticadas, incluyendo la Relatividad General y la Mec??nica Cu??ntica Relativista .

En mec??nica cu??ntica conceptos tales como la fuerza, el impulso y la posici??n se definen por lineal operadores que operan en el estado cu??ntico; a velocidades que son mucho m??s bajos que la velocidad de la luz, las leyes de Newton son tan exacta para estos operadores, ya que son los objetos cl??sicos. A velocidades comparables a la velocidad de la luz, la segunda ley tiene en la forma original 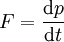, Que dice que la fuerza es la derivada de la din??mica del objeto con respecto al tiempo, pero algunas de las versiones m??s recientes de la segunda ley (como la aproximaci??n de masa constante por encima) no les tomes a velocidades relativistas.

Relaci??n con las leyes de conservaci??n

En la f??sica moderna, las leyes de conservaci??n del impulso , la energ??a y el momento angular son de validez m??s general que las leyes de Newton, ya que se aplican tanto a la luz y la materia, y que tanto la f??sica cl??sica y no cl??sica.

Esto puede afirmar simplemente: "[El impulso, la energ??a, el momento angular, la materia] no puede ser creada ni destruida."

Debido a que la fuerza es la derivada temporal del momento, el concepto de fuerza es redundante y subordinada a la conservaci??n del momento, y no se utiliza en las teor??as fundamentales (por ejemplo, la mec??nica cu??ntica , electrodin??mica cu??ntica, la relatividad general , etc.). El modelo est??ndar explica con detalle c??mo las tres fuerzas fundamentales conocidas como fuerzas calibre se originan fuera del intercambio por part??culas virtuales. Otras fuerzas tales como la gravedad y presi??n de degeneraci??n fermi??nica surgen de las condiciones en las ecuaciones de movimiento en las teor??as subyacentes.

Newton declar?? la tercera ley dentro de una visi??n del mundo que asume la acci??n instant??nea a distancia entre las part??culas materiales. Sin embargo, ??l estaba preparado para la cr??tica filos??fica de esta la acci??n a distancia, y fue en este contexto que, afirm?? la famosa frase " Finjo ninguna hip??tesis ". En la f??sica moderna, la acci??n a distancia se ha eliminado completamente, a excepci??n de los efectos sutiles que implican entrelazamiento cu??ntico.

Conservaci??n de la energ??a fue descubierta casi dos siglos despu??s de la vida de Newton, el gran retraso que ocurre debido a la dificultad en la comprensi??n del papel de las formas microsc??picas e invisibles de energ??a, como el calor y la luz infrarroja.