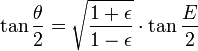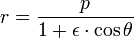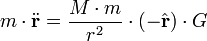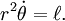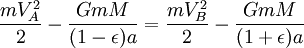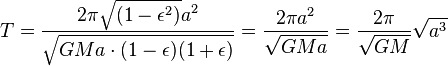Leyes de Kepler

Temas relacionados: Matem??ticas

Antecedentes

SOS ofrecen una descarga completa de esta selecci??n de escuelas para su uso en escuelas intranets. Haga clic aqu?? para obtener informaci??n sobre el apadrinamiento de ni??os.

Ilustraci??n de tres leyes de Kepler con dos ??rbitas planetarias. (1) Las ??rbitas son elipses, con puntos focales f1 y f2 para el primer planeta y f1 y f3 para el segundo planeta. El sol se pone en el punto focal f1. (2) Los dos sectores sombreados A1 y A2 tienen la misma ??rea de superficie y el tiempo para el planeta 1 para cubrir segmento A1 es igual al tiempo para cubrir segmento A2. (3) Los tiempos totales de ??rbita para el planeta y el planeta 1 2 tienen una relaci??n $a1 ^ {3/2}: a2 ^ {3/2}$ .

En astronom??a , leyes de movimiento planetario de Kepler son tres leyes matem??ticas que describen el movimiento de los planetas en el Sistema Solar . Alem??n matem??tico y el astr??nomo Johannes Kepler ( 1571- 1630) las descubrieron.

Kepler estudi?? el observaciones del astr??nomo dan??s precisa legendariamente Tycho Brahe. Alrededor de 1605, Kepler descubri?? que las observaciones de Brahe de las posiciones de los planetas siguieron tres leyes matem??ticas relativamente simples.

Las leyes de Kepler desafiaron la astronom??a y la f??sica aristot??lica y ptolemaica. Su afirmaci??n de que la Tierra se mov??a, su uso de puntos suspensivos en lugar de epiciclos, y su prueba de que las velocidades de los planetas var??an, cambian la astronom??a y la f??sica . Sin embargo, la explicaci??n f??sica de la conducta de los planetas lleg?? casi un siglo m??s tarde, cuando Isaac Newton fue capaz de deducir las leyes de Kepler de las propias de Newton leyes del movimiento y su la ley de la gravitaci??n universal, utilizando su invenci??n del c??lculo . Otros modelos de la gravitaci??n dar??an resultados emp??ricamente falsas.

Tres leyes de Kepler son:

La ??rbita de cada planeta es una elipse con el Sol en uno de los focos. Una elipse se caracteriza por sus dos puntos focales; vea la ilustraci??n. As??, Kepler rechaz?? la antigua aristot??lica, de Ptolomeo, Cop??rnico y la creencia en el movimiento circular.
Una l??nea de unirse a un planeta y el Sol barre ??reas iguales en tiempos iguales como el planeta se desplaza a lo largo de su ??rbita. Esto significa que el planeta viaja m??s r??pido, mientras que cerca del sol y reduce la velocidad cuando se est?? m??s lejos del sol. Con su ley, Kepler destruido la teor??a astron??mica aristot??lica de que los planetas tienen uniforme velocidad .
La plazas de la per??odos orbitales de los planetas son directamente proporcional a la cubos de la semi-ejes principales (el "de longitud media" de la elipse) de sus ??rbitas. Esto significa no s??lo que las ??rbitas m??s grandes tienen per??odos m??s largos, sino tambi??n que la velocidad de un planeta en una ??rbita m??s grande es menor que en una ??rbita m??s peque??a.

Las leyes de Kepler se formulan a continuaci??n, y se derivan de las leyes de Newton, usando helioc??ntricas coordenadas polares $\ (R, \ theta)$ . Sin embargo, las leyes de Kepler, alternativamente, se pueden formular y derivados utilizando coordenadas cartesianas .

Descripci??n matem??tica

Primera ley

La primera ley de Kepler

La primera ley dice: "El ??rbita de cada planeta es una elipse con el Sol en uno de los focos ".

La matem??tica de la elipse es el siguiente.

La ecuaci??n es

$r = \ frac {p} {1+ \ epsilon \ cdot \ cos \ theta}$

donde (r, θ) son las coordenadas polares helioc??ntricas para el planeta, p es el recto semi-latus , y ε es el excentricidad, que es mayor que o igual a cero y menor que uno.

Para θ = 0, el planeta est?? en el perihelio a una distancia m??nima de:

$r_ \ mathrm {min} = \ frac {p} {1+ \ epsilon}$

para θ = 90 ??: r = p, y para θ = 180 ?? del planeta est?? en el afelio a la m??xima distancia:

$r_ \ mathrm {max} = \ frac {p} {1- \ epsilon}$

La semi-eje mayor es la media aritm??tica entre r _min y r _max:

$a = \ frac {p} {1- \ epsilon ^ 2}$

La semi-eje menor es la media geom??trica entre r _min y r _max:

$b = \ frac {p \ sqrt {1- \ epsilon ^ 2}}$

y tambi??n la es media geom??trica entre el semieje mayor y el recto semi latus:

$\ Frac a b = \ frac b p$

Segunda ley

Ilustraci??n de la segunda ley de Kepler.

La segunda ley: "Una l??nea de unirse a un planeta y el Sol barre ??reas iguales en tiempos iguales. "

Esto tambi??n se conoce como la ley de ??reas iguales. Es una consecuencia directa de la ley de conservaci??n del momento angular ; ver la derivaci??n a continuaci??n.

Supongamos que un planeta tarda un d??a para viajar de punto A a B. Las l??neas desde el Sol a A y B, junto con la ??rbita del planeta, definir??n un (m??s o menos triangular ??rea). Esta misma cantidad de ??rea se formar?? cada d??a sin importar donde en su ??rbita el planeta es. Esto significa que el planeta se mueve m??s r??pido cuando se est?? m??s cerca del sol.

Esto se debe a la gravedad del sol acelera el planeta a medida que cae hacia el sol, y se desacelera en el camino de vuelta, pero Kepler no sab??a eso.

Las dos leyes permitieron a Kepler para calcular la posici??n, (r, θ), del planeta, basados en el tiempo transcurrido desde perihelio, t, y el per??odo orbital, P. El c??lculo se realiza en cuatro pasos.

1. Calcular la anomal??a media M de la f??rmula

$M = \ frac {2 \ pi t} {P}$

2. Calcular el exc??ntrica anomal??a E resolviendo num??ricamente la ecuaci??n de Kepler:

$\ M = E \ epsilon \ cdot \ pecado E$

3. Calcular el verdadera θ anomal??a por la ecuaci??n:

$\ Tan \ frac \ theta 2 = \ sqrt {\ frac {1+ \ epsilon} {1- \ epsilon}} \ cdot \ tan \ frac E 2$

4. Calcule la distancia r helioc??ntrica de la primera ley:

$r = \ frac {p 1+ \ epsilon \ cdot \ cos \ theta}$

La prueba de este procedimiento se muestra a continuaci??n.

Tercera ley

La tercera ley: "El plazas de la per??odos orbitales de los planetas son directamente proporcional a la cubos de la semieje mayor de las ??rbitas. "Por lo tanto, no s??lo la longitud de la ??rbita aumenta con la distancia, la velocidad orbital disminuye, por lo que el aumento de la per??odo orbital es m??s que proporcional.

$P ^ 2 \ propto a ^ 3$

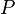$P$ = Per??odo orbital de planeta

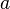$un$ = Semieje mayor de la ??rbita

As?? que la expresi??n de P ² ?? un ^-3 tiene el mismo valor para todos los planetas del Sistema Solar , ya que tiene para la Tierra . Cuando se eligen ciertas unidades, es decir, P se mide en a??o sideral y una en unidades astron??micas, P ² ?? un ^-3 tiene el valor 1 para todos los planetas del Sistema Solar.

En Unidades del SI: $\ Frac {P ^ {2}} {a ^ {3}} = 3,00 \ times 10 ^ {- 19} \ frac {s ^ {2}} {m ^ {3}} \ pm \ 0,7% \,$ .

La ley, cuando se aplica a ??rbitas circulares, donde la aceleraci??n es proporcional a una ?? P ^-2, muestra que la aceleraci??n es proporcional a una ?? un ^-3 = a ^-2, de conformidad con La ley de Newton de la gravitaci??n.

La ecuaci??n general, que Kepler no lo sab??a, es

$\ Left ({\ frac {P} {2 \ pi}} \ right) ^ 2 = {a ^ 3 \ over G (M + m)},$

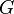donde $G$ es la constante gravitacional, 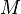$M$ es la masa del Sol, y 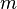$m$ es la masa del planeta. Este ??ltimo aparece en la ecuaci??n ya que la ecuaci??n de movimiento implica el reducci??n de la masa. Tenga en cuenta que P es el tiempo por ??rbita y P / 2π es momento por radi??n .

Ver las cifras reales: atributos de los planetas mayores.

Esta ley tambi??n se conoce como la ley arm??nica.

Posici??n como una funci??n del tiempo

El problema kepleriano asume un ??rbita el??ptica y los cuatro puntos:

s el sol (en uno de los focos de la elipse);
z el perihelio
c el centro de la elipse
p el planeta

$\ A = | cz |,$ distancia desde el centro hacia el perihelio, el semieje mayor,

$\ \ Varepsilon = {| cs | \ over a},$ la excentricidad,

$\ B = a \ sqrt {1- \ varepsilon ^ 2},$ los semieje menor,

$\ R = | sp |,$ la distancia del sol en planeta.

y el ??ngulo

$\ Nu = \ zsp ??ngulo,$ el planeta visto desde el sol, la anomal??a verdadera.

El problema consiste en calcular las coordenadas polares (r, ν) del planeta desde el tiempo transcurrido desde el perihelio, t.

Se resuelve en pasos. Kepler comenz?? mediante la adici??n de c??rculo auxiliar de la ??rbita (que con el eje mayor como di??metro) y define estos puntos:

x es la proyecci??n del planeta al c??rculo auxiliar; entonces el ??rea $| ZSX | = \ frac una b \ cdot | zsp |$
y es un punto en el c??rculo auxiliar tal que el ??rea $\ | Zcy | = | ZSX |$

$M = \ zcy ??ngulo$ , Y como se ve desde el centro, el anomal??a media.

El ??rea de la sector circular $\ | Zcy | = \ frac {a ^ 2 M 2}$ , Y el ??rea barrida desde el perihelio,

$| Zsp | = \ frac ba \ cdot | ZSX | = \ frac ba \ cdot | zcy | = \ frac ba \ cdot \ frac {a ^ 2} M 2 = \ frac {ab M} {2}$ ,

es por segunda proporcional ley de Kepler en cuando desde el perihelio. As?? que la anomal??a media, M, es proporcional al tiempo transcurrido desde el perihelio, t.

$M = {2 \ pi t \ over T}$

donde T es el per??odo orbital.

La anomal??a media M se calcula en primer lugar. El objetivo es calcular la verdadera ν anomal??a. La funci??n ν = f (M) es, sin embargo, no elemental. Soluci??n de Kepler es utilizar

$E = \ zcx ??ngulo$ , X como se ve desde el centro, el anomal??a exc??ntrica

como una variable intermedia, y primero compute E como una funci??n de M mediante la resoluci??n de la ecuaci??n de Kepler a continuaci??n, y luego calcular la anomal??a verdadera ν de la anomal??a exc??ntrica E. Aqu?? est??n los detalles.

$\ | Zcy | = | ZSX | = | zcx | - | scx |$

$\ Frac {a ^ 2} M 2 = \ frac {a ^ 2 E} 2- \ frac {a \ varepsilon \ cdot un \ pecado E} 2$

Divisi??n por un ?? / 2 da la ecuaci??n de Kepler

$M = E \ varepsilon \ cdot \ pecado E$ .

El problema es que la ecuaci??n de Kepler no puede ser reorganizado para aislar E. La funci??n E = f (M) no es una f??rmula elemental. La ecuaci??n de Kepler se resuelve iterativamente ya sea por una Resoluci??n num??rica de ecuaciones no lineales o, como se deriva en el art??culo sobre anomal??a exc??ntrica, por una serie infinita

$E \ aprox M + \ left (\ varepsilon- \ frac18 \ varepsilon ^ 3 \ right) \ pecado M + \ frac12 \ varepsilon ^ 2 \ sin 2M + \ frac38 \ varepsilon ^ 3 \ pecado 3M + \ cdots$

Para el peque??o ε t??pico de los planetas (excepto Plut??n ), dichas series son bastante precisa con s??lo unos pocos t??rminos.

Habiendo calculado la anomal??a exc??ntrica E de la ecuaci??n de Kepler, el siguiente paso es calcular la anomal??a verdadera ν de la anomal??a exc??ntrica E.

Nota de la geometr??a del problema que

$a \ cdot \ cos E = a \ cdot \ varepsilon + r \ cdot \ cos \ nu.$

Dividiendo por una y la inserci??n de la primera ley de Kepler

$\ \ Frac ra = \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}$

llegar

$\ Cos E = \ varepsilon + \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu} \ cdot \ cos \ nu = \ frac {\ varepsilon \ cdot (1+ \ varepsilon \ cdot \ cos \ nu) + (1- \ varepsilon ^ 2) \ cdot \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu} = \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}.$

El resultado es una relaci??n utilizable entre la anomal??a exc??ntrica E y el verdadero ν anomal??a.

Una forma computacionalmente m??s conveniente sigue sustituyendo en el identidad trigonom??trica:

$\ Tan ^ 2 \ frac {x} {2} = \ frac {1- \ cos x} {1+ \ cos x}.$

Llegar

$\ Tan ^ 2 \ frac {E} {2} = \ frac {1- \ cos E} {1+ \ cos E} = \ frac {1- \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} {1+ \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} = \ frac {(1+ \ varepsilon \ cdot \ cos \ nu) - (\ varepsilon + \ cos \ nu)} {(1+ \ varepsilon \ cdot \ cos \ nu) + (\ varepsilon + \ cos \ nu)} = \ frac {1- \ varepsilon} {1+ \ varepsilon} \ cdot \ frac {1- \ cos \ nu} {1+ \ cos \ nu} = \ frac {1- \ varepsilon} {1+ \ varepsilon} \ cdot \ tan ^ 2 \ frac {\ nu} {2}.$

Multiplicando por (1 + ε) / (1-ε) y tomando la ra??z cuadrada da el resultado

$\ Tan \ frac \ nu2 = \ sqrt \ frac {1+ \ varepsilon} {1- \ varepsilon} \ cdot \ tan \ frac E2.$

Hemos completado el tercer paso en la conexi??n entre el tiempo y la posici??n en la ??rbita.

Incluso se podr??a desarrollar una serie de computaci??n ν directamente de M.

El cuarto paso es calcular la distancia r helioc??ntrica de la verdadera ν anomal??a por la primera ley de Kepler:

$\ R = a \ cdot \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}.$

Derivaci??n de las leyes de Newton

Las leyes de Kepler son sobre el movimiento de los planetas alrededor del sol, mientras que las leyes de Newton son m??s generalmente sobre el movimiento de las part??culas puntuales atraerse entre s?? por la fuerza de la gravitaci??n . En el caso especial en que s??lo hay dos part??culas, y una de ellas es mucho m??s ligero que el otro, y la distancia entre las part??culas sigue siendo limitada, entonces la part??cula se mueve m??s claras alrededor de la part??cula pesada como un planeta alrededor del sol de acuerdo con las leyes de Kepler , como se muestra abajo. Las leyes de Newton sin embargo tambi??n admiten otras soluciones, en donde la trayectoria de la part??cula m??s ligero es una par??bola o una hip??rbola. Estas soluciones muestran que hay una limitaci??n a la aplicabilidad de la primera ley de Kepler, que establece que la trayectoria siempre ser?? una elipse. En el caso de que una part??cula no es mucho m??s ligero que el otro, resulta que cada part??cula se mueve alrededor de su com??n centro de masa , por lo que el general dos problema cuerpo se reduce al caso especial donde una part??cula es mucho m??s ligero que el otro. Si bien las leyes de Kepler se expresan en lenguaje geom??trico o como ecuaciones que conectan las coordenadas del planeta y la variable tiempo con la elementos orbitales, la segunda ley de Newton es una ecuaci??n diferencial . As?? las derivaciones inferiores implican el arte de resolver ecuaciones diferenciales. La segunda ley se deriva en primer lugar, como la derivaci??n de la primera ley depende de la derivaci??n de la segunda ley.

Derivaci??n de la segunda ley de Kepler

La ley de la gravitaci??n de Newton dice que "cada objeto en el universo atrae a todos los dem??s objetos a lo largo de una l??nea de los centros de los objetos, de forma proporcional a la masa de cada objeto, e inversamente proporcional al cuadrado de la distancia entre los objetos", y su segunda ley de movimiento dice que "la masa por la aceleraci??n es igual a la fuerza". As?? la masa de los tiempos planeta el vector aceleraci??n del planeta es igual a la masa de los tiempos dom la masa del planeta, dividido por el cuadrado de la distancia, los tiempos menos el radial vector unitario, los tiempos de una constante de proporcionalidad. Esto est?? escrito:

$m \ cdot \ ddot \ mathbf {r} = \ frac {M \ cdot m} {r ^ 2} \ cdot (- \ hat {\ mathbf {r}}) \ cdot G$

donde un punto en la parte superior de la variable significa la diferenciaci??n con respecto al tiempo, y el segundo punto indica la segunda derivada.

Supongamos que el planeta es mucho m??s ligero que el sol que la aceleraci??n del sol puede ser descuidado.

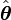$\ Dot \ hat {\ mathbf {r}} = \ dot \ theta \ hat {\ boldsymbol \ theta}$

donde $\ Hat {\ boldsymbol \ theta}$ es el vector unitario tangencial, y

$\ Dot \ hat {\ boldsymbol \ theta} = - \ dot \ theta \ hat {\ mathbf {r}}.$

As?? el vector de posici??n

$\ Mathbf {r} = r \ hat {\ mathbf {r}}$

se diferencia dos veces para dar el vector de velocidad y el vector de aceleraci??n

$\ Dot \ mathbf {r} = \ dot r \ hat \ mathbf {r} + r \ dot \ hat \ mathbf {r} = \ dot r \ hat {\ mathbf {r}} + r \ dot \ theta \ hat {\ boldsymbol \ theta},$

$\ Ddot \ mathbf {r} = (\ ddot r \ hat {\ mathbf {r}} + \ dot r \ dot \ hat {\ mathbf {r}}) + (\ dot r \ dot \ theta \ hat {\ boldsymbol \ theta} + r \ ddot \ theta \ hat {\ boldsymbol \ theta} + r \ dot \ theta \ dot \ hat {\ boldsymbol \ theta}) = (\ ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta}.$

Tenga en cuenta que para la distancia constante, $\ R$ , El planeta est?? sujeto a la aceleraci??n centr??peta , $r \ dot \ theta ^ 2$ Y para la velocidad angular constante, $\ Dot \ theta$ , El planeta est?? sujeto a la aceleraci??n de Coriolis, $2 \ dot r \ dot \ theta$ .

Inserci??n del vector aceleraci??n en las leyes de Newton, y dividiendo por m, da el vector ecuaci??n de movimiento

$(\ Ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta} = -GMr ^ {- 2} \ hat {\ mathbf {r}}$

Igualando componente, obtenemos las dos ecuaciones diferenciales ordinarias de movimiento, uno para la aceleraci??n radial y uno para la aceleraci??n tangencial:

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2},$

$r \ ddot \ theta + 2 \ dot r \ dot \ theta = 0.$

Con el fin de obtener la segunda ley de Kepler s??lo se necesita la ecuaci??n de la aceleraci??n tangencial. Dividirlo por $\ R \ dot \ theta:$

$\ Frac {\ ddot \ theta} {\ dot \ theta} 2 \ frac {\ dot r} {r} = 0$

e integrar:

$\ Log \ dot \ theta 2 \ log r = \ log \ ell,$

donde $\ Log \ ell$ es un constante de integraci??n, y exponenciar:

$r ^ 2 \ dot \ theta = \ ell.$

Esto dice que la momento angular espec??fica $r ^ 2 \ dot \ theta$ es un constante de movimiento, incluso si tanto la distancia $\ R$ y la velocidad angular $\ Dot \ theta$ variar.

El ??rea barrida de vez en cuando t ₁ t _2,

$\ \ Int_ {t_1} ^ {t_2} \ frac 1 2 \ cdot altura de la base \ cdot \ cdot dt = \ {int_ t_1} ^ {t_2} \ frac 1 2 \ cdot r \ cdot r \ dot \ theta \ cdot dt = \ frac 1 2 \ cdot \ ell \ cdot (t_2-t_1)$

depende s??lo de la duraci??n t ₂ - t _1. Esta es la segunda ley de Kepler.

Derivando la primera ley de Kepler

La expresi??n

$p = \ ell ^ 2 G ^ {- 1} M ^ {- 1}$

tiene la dimensi??n de la longitud y se utiliza para hacer las ecuaciones de movimiento adimensional. Definimos

$\ U = pr ^ {- 1}$

y obtener

$-GMr ^ {- 2} = - \ ell ^ 2 p ^ {- 3} u ^ {2}$

$\ \ Dot \ theta = \ ell r ^ {- 2} = \ ell p ^ {- 2} u ^ 2.$

La diferenciaci??n con respecto al tiempo se transforma en la diferenciaci??n con respecto al ??ngulo:

$\ \ El punto X = \ frac {dx} {d \ theta} \ cdot \ dot \ theta = \ frac {dx} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ 2.$

Diferenciar

$\ R = pu ^ {- 1}$

dos veces:

$\ El punto r = \ frac {d (pu ^ {- 1})} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = -pu ^ {- 2} \ frac {du} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = - \ ell p ^ {- 1} \ frac {du} {d \ theta}$

$\ Ddot r = \ frac {d \ dot r} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = \ frac {d} {d \ theta} (- \ ell ^ p { -1} \ frac {du} {d \ theta}) \ cdot \ ell p ^ {- 2} u ^ {2} = - \ ell ^ 2 p ^ {- 3} u ^ {2} \ frac {d ^ 2 u} {d \ theta ^ 2}$

Sustituye en la ecuaci??n radial de movimiento

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2}$

y obtener

$(- \ Ell ^ 2 p ^ {- 3} u ^ 2 \ frac {d ^ 2u} {d \ theta ^ 2}) - (pu ^ {- 1}) (\ ell p ^ {- 2} u ^ 2) ^ 2 = - \ ell ^ 2 p ^ {- 3} u ^ 2$

Dividido por $- \ Ell ^ 2 p ^ {- 3} u ^ 2$ para conseguir una sencilla ecuaci??n diferencial lineal no homog??nea de la ??rbita del planeta:

$\ Frac {d ^ 2u} {d \ theta ^ 2} + u = 1.$

Una soluci??n obvia a esta ecuaci??n es la ??rbita circular

$\ U = 1.$

Otras soluciones se obtienen mediante la adici??n de soluciones a la ecuaci??n diferencial lineal homog??nea con coeficientes constantes

$\ Frac {d ^ 2u} {d \ theta ^ 2} + u = 0$

Estas soluciones son

$\ U = \ epsilon \ cdot \ cos (\ theta-A)$

donde $\ \ Epsilon$ y $\ A$ son constantes arbitrarias de la integraci??n. As??, el resultado es

$\ U = 1 + \ epsilon \ cdot \ cos (\ theta-A)$

Elegir el eje de la tal sistema de coordenadas que $\ A = 0$ Y la inserci??n de $\ U = pr ^ {- 1}$ , Se obtiene:

$\ Pr ^ {- 1} = 1 + \ epsilon \ cdot \ cos \ theta.$

Si $\ \ Epsilon <1,$ esta es la primera ley de Kepler.

La tercera ley de Kepler

Newton utiliz?? la tercera ley como uno de los elementos de prueba que se utilizan para construir el marco conceptual y matem??tico de la Ley de la Gravitaci??n. Si tomamos las leyes del movimiento de Newton como un hecho, y consideramos un hipot??tico planeta que pasa a estar en una ??rbita perfectamente circular de radio r, entonces tenemos $F = mv ^ 2 / r$ por la fuerza del sol en el planeta. La velocidad es proporcional a r / T, que por la tercera ley de Kepler var??a como uno m??s de la ra??z cuadrada de r. Sustituyendo esto en la ecuaci??n de la fuerza, nos encontramos con que la fuerza de la gravedad es proporcional a uno sobre r al cuadrado. Cadena hist??rica real de Newton de razonamiento no se conoce con certeza, porque en su escritura tend??a a borrar cualquier rastro de c??mo hab??a llegado a sus conclusiones. La inversi??n del sentido de razonamiento, podemos considerar esto como una prueba de la tercera ley de Kepler basado en la ley de la gravedad, y el cuidado de los factores de proporcionalidad que fueron descuidados en el argumento anterior de Newton, tenemos:

$T ^ 2 = \ frac {4 \ pi ^ 2} {GM} \ cdot r ^ 3$

donde:

T = planeta de periodo sideral
r = radio de la ??rbita circular del planeta
G = el constante gravitacional
M = masa del Sol

Los mismos argumentos se pueden aplicar a cualquier objeto en ??rbita cualquier otro objeto. Esta discusi??n asume impl??citamente que el planeta orbita alrededor del Sol estacionario, aunque en realidad tanto el planeta y el Sol giran alrededor de su centro de masa com??n. Newton reconoci?? esto, y modific?? esta tercera ley, se??alando que el per??odo tambi??n se ve afectada por el cuerpo en ??rbita masa . Sin embargo normalmente el cuerpo central es mucho m??s masiva que la masa del cuerpo en ??rbita puede ser ignorada. Newton tambi??n demostr?? que en el caso de una ??rbita el??ptica, la semimayor eje podr??a ser sustituido por el radio. El resultado m??s general es:

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} \ cdot a ^ 3$

donde:

T = objeto de periodo sideral
a = objeto del semieje mayor
G = el constante gravitacional = 6,67 ?? 10 ^-11 N ??? m?? / kg??
M = masa de un objeto
m = masa del otro objeto

Para los objetos que orbitan alrededor del sol, puede ser conveniente utilizar unidades de a??o, la Uni??n Africana, y masas solares, por lo que G, 4π?? y los diversos factores de conversi??n se cancelan. Tambi??n con m << M podemos establecer m + M = M, as?? que tenemos simplemente $T ^ 2 = a ^ 3$ . Tenga en cuenta que los valores de G y masas planetarias no se conocen con buena precisi??n; Sin embargo, los productos transg??nicos (la atracci??n kepleriano) son conocidos por una precisi??n extremadamente alta.

Definir el punto A al ser el periapsis, y el punto B como la apoapsis del planeta al orbitar el sol.

La segunda ley de Kepler establece que el cuerpo orbitando barrer?? ??reas iguales en cantidades iguales de tiempo. Si ahora miramos unos muy peque??os per??odos de tiempo en los momentos en que el planeta se encuentra en los puntos A y B, entonces podemos aproximar el ??rea barrida como un tri??ngulo con una altura igual a la distancia entre el planeta y el sol, y la base igual a la vez que la velocidad del planeta.

$\ Begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot (1- \ epsilon) a \ cdot V_A \, dt = \ begin {matriz} \ frac {1} {2} \ end { matriz} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt$

$(1- \ epsilon) \ cdot V_A = (1+ \ epsilon) \ cdot V_B$

$V_A = V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon}$

Usando el ley de la conservaci??n de la energ??a para la energ??a total del planeta en los puntos A y B,

$\ Frac {mV_A ^ 2} {2} - \ frac {} {GmM (1- \ epsilon) a} = \ frac {mV_B ^ 2} {2} - \ frac {} {GmM (1+ \ epsilon) un }$

$\ Frac {V_A ^ 2} {2} - \ frac {V_B ^ 2} {2} = frac {GM} {(1- \ epsilon) a} \ - \ frac {GM} {(1+ \ epsilon) un }$

$\ Frac {V_A ^ 2-V_B ^ 2} {2} = \ frac {GM} {a} \ cdot \ left (\ frac {1} {(1- \ epsilon)} - \ frac {1} {(1 + \ epsilon)} \ right)$

$\ Frac {\ dej?? (V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2} {2} = \ frac {GM} {a} \ cdot \ left ( \ frac {1+ \ epsilon-1 + \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2 = \ {a} \ cdot \ left (\ frac frac {2GM} {2 \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {(1+ \ epsilon) ^ 2- (1- \ epsilon) ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot \ left (\ frac {1 + 2 \ epsilon + \ epsilon ^ 2-1 + 2 \ epsilon \ epsilon ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot 4 \ epsilon = \ frac {4GM \ epsilon \ cdot (1- \ epsilon) ^ 2} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B = \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}}.$

Ahora que tenemos $V_B$ , Podemos encontrar la velocidad a la que el planeta est?? barriendo a cabo en el ??rea de la elipse. Esta tasa se mantiene constante, por lo que podemos deducir que desde cualquier punto que queremos, espec??ficamente desde el punto B.

$\ Frac {dA} {dt} = \ frac {\ frac {1} {2} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt} {dt} = \ begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot (1+ \ epsilon) a \ cdot V_B$

$= \ Begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot (1+ \ epsilon) a \ cdot \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}} = \ begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot \ sqrt {GMA \ cdot (1- \ epsilon) (1+ \ epsilon)}$

Sin embargo, el ??rea total de la elipse es igual a $\ Pi a \ sqrt {(1- \ epsilon ^ 2)} un$ . (Eso es lo mismo que $\ Pi a b$ , Porque $b = \ sqrt {(1- \ epsilon ^ 2)} un$ ). El tiempo que el planeta sacar para barrer toda el ??rea de la elipse es igual ??rea de la elipse, as??,

$T \ cdot \ frac {dA} {dt} = \ pi a \ sqrt {(1- \ epsilon ^ 2)} un$

$T \ cdot \ begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot \ sqrt {GMA \ cdot (1- \ epsilon) (1+ \ epsilon)} = \ pi \ sqrt {(1 - \ epsilon ^ 2)} a ^ 2$

$T = \ frac {2 \ pi \ sqrt {(1- \ epsilon ^ 2)} a ^ 2} {\ sqrt {GMA \ cdot (1- \ epsilon) (1+ \ epsilon)}} = \ frac {2 \ pi a ^ 2} {\ sqrt {GMA}} = \ frac {2 \ pi} {\ sqrt {GM}} \ sqrt {a ^ 3}$

$T ^ 2 = \ frac {4 \ pi ^ 2} {GM} a ^ 3.$

Sin embargo, si la masa m no es insignificante en relaci??n con M, entonces el planeta orbita el sol con la misma velocidad y la posici??n exacta como un cuerpo muy peque??o en ??rbita un objeto de masa $M + m$ (Ver reducci??n de la masa). Para integrar que en la f??rmula anterior, M debe ser reemplazado con $M + m$ , Dar

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} a ^ 3.$

QED

Recuperado de " http://en.wikipedia.org/w/index.php?title=Kepler%27s_laws_of_planetary_motion&oldid=198683410 "