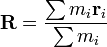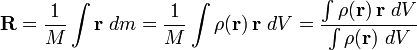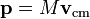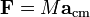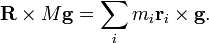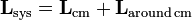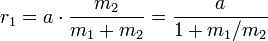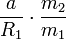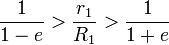Centro de masa

Temas relacionados: Matemáticas

Sabías ...

SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. SOS Children es la caridad más grande del mundo dando a los niños huérfanos y abandonados de la oportunidad de la vida familiar.

En la física , el centro de masa de un sistema de partículas es un punto específico en el que, para muchos propósitos, el sistema de masa se comporta como si se concentraron. El centro de masa es una función sólo de las posiciones y las masas de las partículas que componen el sistema. En el caso de una cuerpo rígido, la posición de su centro de masa se fija en relación con el objeto (pero no necesariamente en contacto con ella). En el caso de una distribución de masas en la suelta el espacio libre, tal como, por ejemplo, Disparo de un escopeta, la posición del centro de masa es un punto en el espacio entre ellos que pueden no corresponder a la posición de cualquier masa individual. En el contexto de un campo gravitatorio totalmente uniforme, el centro de masa se llama a menudo el centro de gravedad - el punto donde la gravedad se puede decir que actuar.

El centro de masa de un cuerpo no siempre coincide con su centro geométrico intuitiva, y se puede explotar esta libertad. Los ingenieros tratan de diseñar un centro coche deportivo de gravedad lo más bajo posible para hacer el coche manejar mejor. Cuando saltadores realizan un " Fosbury Flop ", hicieron que su cuerpo de tal manera que es posible que el puente para borrar el bar mientras su centro de masa no lo hace.

El llamado el centro del cuadro de gravedad (un término menos preferida para el el centro del marco impulso) es una marco de inercia definido como el marco inercial en el que el centro de masa de un sistema está en reposo.

Definición

El centro de masa 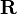$\ Mathbf {R}$ de un sistema de partículas se define como la promedio de sus posiciones 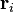$\ Mathbf {r} _i$ , ponderados por sus masas $m_i$ :

$\ Mathbf {R} = {\ sum m_i \ mathbf {r} _i \ sobre \ suma m_i}$

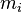Para distribución continua con densidad de masa 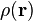$\ Rho (\ mathbf {r})$ y masa total 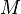$M$ , La suma se convierte en una integral:

$\ Mathbf R = \ frac 1 M \ int \ mathbf {r} \; dm = \ frac 1 M \ int \ rho (\ mathbf {r}) \, \ mathbf {r} \ dV = \ frac {\ int \ rho (\ mathbf {r}) \, \ mathbf {r} \ dV} {\ int \ rho (\ mathbf {r}) \ dV}$

Si un objeto tiene uniforme de densidad a continuación, su centro de masa es la misma que la centro de gravedad de su forma.

Ejemplos

El centro de masa de un sistema de dos partículas se encuentra en la línea que une las partículas (o, más precisamente, sus centros individuales de masa). El centro de masa está más cerca del objeto más masivo; Para más detalles, consulte baricentro a continuación.
El centro de masa de un anillo está en el centro del anillo (en el aire).
El centro de masa de un triángulo sólido se encuentra en los tres medianas y por lo tanto en el centroide, que es también la media de los tres vértices.
El centro de masa de un rectángulo es en la intersección de las dos diagonales.
En un cuerpo con simetría esférica, el centro de masa está en el centro. Esto se aplica aproximadamente a la Tierra : la densidad varía considerablemente, pero depende principalmente de la profundidad y menos en las otras dos coordenadas.
Más en general, para cualquier simetría de un cuerpo, su centro de masa será un punto de que la simetría fijo.

Historia

El concepto de centro de gravedad se introdujo por primera vez por los antiguos griegos matemático, físico e ingeniero Arquímedes de Siracusa . Arquímedes mostró que la de par ejercida sobre una palanca de pesos que descansan en varios puntos a lo largo de la palanca es lo mismo que lo que sería si todos los pesos fueron trasladados a un solo punto - su centro de gravedad. En el trabajo en cuerpos flotantes que demostró que la orientación de un objeto flotante es la que hace que su centro de gravedad tan bajo como sea posible. Desarrolló técnicas matemáticas para encontrar los centros de gravedad de los objetos de la densidad uniforme de varias formas bien definidas, en particular, un triángulo, un hemisferio, y un tronco de un paraboloide circular.

En la Edad Media , las teorías sobre el centro de gravedad fueron desarrolladas por Al-Biruni, al-Razi ( latinizado como Razi), Omar Khayyam, y al-Khazini.

Movimiento

Las siguientes ecuaciones de movimiento asumen que hay un sistema de partículas que se rigen por fuerzas internas y externas. Una fuerza es una fuerza interna causada por la interacción de las partículas dentro del sistema. Una fuerza externa es una fuerza que se origina desde fuera del sistema, y actúa sobre una o más partículas dentro del sistema. La fuerza externa no necesita ser debido a un campo uniforme.

Para cualquier sistema sin fuerzas externas, el centro de masa se mueve con velocidad constante. Esto se aplica para todos los sistemas con fuerzas internas clásicos, incluyendo campos magnéticos, campos eléctricos, reacciones químicas, y así sucesivamente. Más formalmente, esto es cierto para todas las fuerzas internas que satisfacen la forma débil de la tercera ley de Newton .

El momento total para cualquier sistema de partículas viene dada por

$\ Mathbf {p} = M \ mathbf {v} _ \ mathrm {cm}$

Donde M indica la masa total, y v es la velocidad _cm del centro de la masa. Esta velocidad se puede calcular tomando la derivada temporal de la posición del centro de masa.

Un análogo a la famosa Segunda Ley de Newton es

$\ Mathbf {F} = M \ mathbf {a} _ \ mathrm {cm}$

Donde F indica la suma de todas las fuerzas externas en el sistema, y un _cm indica la aceleración del centro de masa.

Rotación y centros de gravedad

Diagrama de un juguete educativo que equilibra en un punto: el CM (C) se instala por debajo de su soporte (P). Cualquier objeto cuyo CM está por debajo del punto de apoyo no se mueva.

El centro de masa se llama a menudo el centro de gravedad debido a que cualquier uniforme Campo de Gravedad G actúa sobre un sistema como si la masa M del sistema se concentraron en el centro de masa R. Esto se ve en al menos dos formas:

La energía potencial gravitatoria de un sistema es igual a la energía potencial de una partícula puntual que tienen la misma masa M situado en R.
El gravitacional de par en un sistema es igual a la par de una fuerza M g que actúa en R:
$\ Mathbf {R} \ épocas M \ mathbf {g} = \ sum_im_i \ mathbf {r} _i \ times \ mathbf {g}.$

Si el campo gravitacional que actúa sobre un cuerpo no es uniforme, entonces el centro de masa no exhibe necesariamente estas propiedades convenientes en relación con la gravedad. A medida que la situación se pone en Feynman libro influyente 's The Feynman Lectures on Physics:

"El centro de masa se denomina a veces el centro de gravedad, por la razón de que, en muchos casos, la gravedad puede ser considerado uniforme. ... En caso de que el objeto es tan grande que el nonparallelism de las fuerzas gravitacionales es significativo, entonces el centro en el que hay que aplicar la fuerza de equilibrio no es fácil de describir, y se aparta ligeramente del centro de masa. Es por eso que hay que distinguir entre el centro de masa y el centro de gravedad. "

Autores posteriores suelen ser menos cuidadoso, afirmando que cuando la gravedad no es uniforme, "el centro de gravedad" se aparta de la CM. Este uso parece implicar un "centro de gravedad" concepto de campos no uniformes bien definido, pero no hay tal cosa. Incluso cuando se considera las fuerzas de marea de planetas , es suficiente utilizar centros de masa para encontrar el movimiento global. En la práctica, para los campos no uniformes, uno simplemente no se habla de un "centro de gravedad".

Marco CM

El momento angular del vector para un sistema es igual al momento angular de todas las partículas alrededor del centro de masa, más el momento angular del centro de masa, como si se tratara de una sola partícula de masa 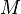$M$ :

$\ Mathbf {L} _ \ mathrm {sys} = \ mathbf {L} _ \ mathrm {cm} + \ mathbf {L} _ \ mathrm {torno \, cm}$

Este es un corolario de la Parallel Axis Teorema.

Ingeniería

Importancia aeronáutica

El centro de masa es un punto importante en una aeronave , que afecta significativamente la estabilidad de la aeronave. Para asegurar que el avión es seguro volar, es crítico que el centro de caída por gravedad dentro de los límites especificados. Este rango varía por las aeronaves, pero como regla general que se centra alrededor de un punto cuarto de la distancia desde el borde del ala que lleva al borde de salida del ala (el punto de acordes trimestre). Si el centro de gravedad está por delante del límite hacia adelante, la aeronave será menos maniobrable, posiblemente hasta el punto de no poder girar para el despegue o el aterrizaje,. Si el centro de masa está detrás del límite de popa, el brazo de momento de la ascensor se reduce, lo que hace más difícil recuperarse de una estado estancado. La aeronave será más maniobrable, pero también menos estable, y posiblemente tan inestable que es imposible para volar.

Baricentro en astronomía

El baricentro (o baricentro; del griego βαρύκεντρον) es el punto entre dos objetos donde se equilibran entre sí. En otras palabras, el centro de gravedad cuando dos o más cuerpos celestes orbitan entre sí. Cuando una Luna orbita alrededor de una planeta , o un planeta orbita alrededor de una estrella , ambos cuerpos están realmente orbitando alrededor de un punto que se encuentra fuera del centro de la mayor cuerpo. Por ejemplo, la luna no está en órbita el centro exacto de la tierra, en vez en órbita un punto fuera del centro de la tierra (pero muy por debajo de la superficie de la Tierra), donde sus respectivas masas se equilibran entre sí. El baricentro es una de las focos de la órbita elíptica de cada cuerpo. Este es un concepto importante en el campo de la astronomía , la astrofísica , y similares (véase problema de dos cuerpos).

En un caso simple de dos cuerpos, r _1, la distancia desde el centro de la primera cuerpo para el baricentro está dada por:

$r_1 = a \ cdot {m_2 \ sobre m_1 + m_2} = {a \ más de 1 + m_1 / m_2}$

donde:

a es la distancia entre los centros de los dos cuerpos;

m ₁ y m ₂ son las masas de los dos cuerpos.

r ₁ es esencialmente el semieje mayor de la órbita del primer cuerpo alrededor del baricentro - y r ₂ = a - r ₁ del semieje mayor de la órbita del segundo cuerpo. Cuando el baricentro se encuentra dentro del cuerpo más masivo, ese cuerpo aparecerá al "bamboleo" en lugar de seguir una órbita discernible.

La siguiente tabla muestra algunos ejemplos de nuestro sistema solar . Las cifras se dan redondeado a tres personajes importantes. Las dos últimas columnas muestran R _1, el radio de la primera (más masiva) del cuerpo, y r ₁ / R _1, la relación de la distancia al baricentro y de ese radio: un valor inferior a uno indica que el baricentro se encuentra dentro de la primer cuerpo.

**Ejemplos**
Ampliar cuerpo	m ₁ (M _E = 1)	Menor cuerpo	m ₂ (M _E = 1)	un ( km)	r ₁ (Km)	R ₁ (Km)	r ₁ / R ₁
Observaciones
Tierra	1	Luna	0.0123	384000	4670	6380	0,732
La Tierra tiene un "bamboleo" perceptible.
Plutón	0.0021	Caronte	0.000,254 (0.121 m _Plutón)	19600	2110	1150	1.83
Ambos cuerpos tienen órbitas distintas alrededor del baricentro, y como tales Plutón y Caronte se consideraron como planeta doble por muchos antes de la redefinición de planeta en agosto de 2006.
Sol	333000	Tierra	1	150000000 (1 AU)	449	696000	0.000,646
Bamboleo del Sol es apenas perceptible.
Sol	333000	Júpiter	318	778000000 (5.20 UA)	742000	696000	1.07
El Sol gira alrededor de un baricentro justo por encima de su superficie.

Si m ₁ >> m ₂ - que es cierto para el Sol y todos los planetas - entonces la relación r ₁ / _R1 se aproxima a:

${A \ sobre R_1} \ cdot {m_2 \ sobre m_1}$

Por lo tanto, el baricentro del sistema Sol-planeta se encontrará fuera del Sol sólo si:

${A \ más de R _ {\ bigodot}} \ cdot {m_ {planeta} \ over m _ {\ bigodot}}> 1 \; \ Flecha Correcta \; {A m_ \ cdot {planeta}}> {R _ {\ bigodot} \ cdot m _ {\ bigodot}} \ aproximadamente 2,3 \ times 10 ^ {11} \; m_ {Tierra} \; \ Mbox {km} \ aprox 1530 \; m_ {Tierra} \; \ Mbox {AU}$

Es decir, donde el planeta es pesado y lejos del Sol

Si Júpiter tenía Mercurio orbita 's (57.900.000 kilometros, 0,387 UA), el baricentro Sol-Júpiter sería sólo 5.500 km y el centro del Sol (r ₁ / R ₁ ~ 0.08). Pero incluso si la Tierra tuviera Eris órbita '(68 UA), el baricentro Sol-Tierra todavía estaría dentro del Sol (algo más de 30.000 kilometros del centro).

Para calcular el movimiento real del Sol, lo que se necesita para resumir todas las influencias de todos los planetas , cometas , asteroides , etc., del sistema solar (ver Problema de los tres cuerpos). Si todos los planetas estaban alineados en el mismo lado del Sol, el centro de la masa combinada sería mentir alrededor de 500.000 km por encima de la superficie del Sol.

Los cálculos anteriores se basan en la distancia media entre los cuerpos y ceden el valor medio r _1. Pero todas las órbitas celestes son elípticas, y la distancia entre los cuerpos varía entre el ábsides, dependiendo de la excentricidad, e. Por lo tanto, la posición del baricentro varía demasiado, y es posible en algunos sistemas para el baricentro a ser a veces dentro y fuera del cuerpo a veces más masivo. Esto ocurre cuando:

${1 \ over {1-e}}> {r_1 \ sobre R_1}> {1 \ over {1 + e}}$

Tenga en cuenta que el sistema Sol-Júpiter, con _Júpiter e = 0.0484, sólo no se clasifica: 1,05 ≯ 1,07> 0,954.

Animaciones

Las imágenes son representativas, no simuladas.

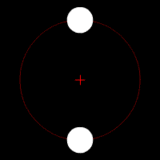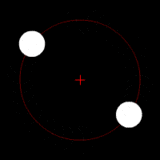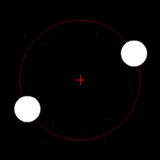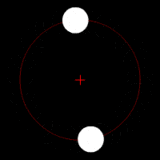Dos cuerpos de masa similar en órbita alrededor de un baricentro común. (Similar a la 90 sistema Antíope)	Dos cuerpos con una diferencia en órbita alrededor de una masa baricentro común, como en el de Plutón - Sistema de Caronte.	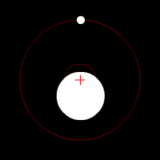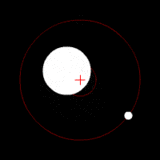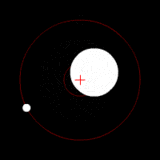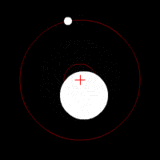Dos cuerpos con una gran diferencia en órbita alrededor de una masa baricentro común (similar a la Tierra - Luna sistema)	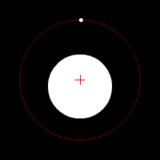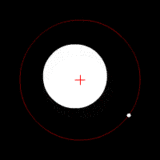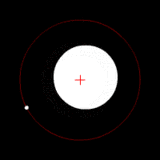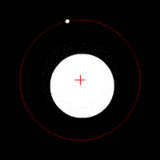Dos cuerpos con una diferencia extrema en órbita alrededor de una masa baricentro común (similares al Sol - Tierra del sistema)
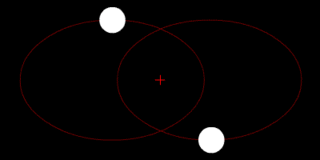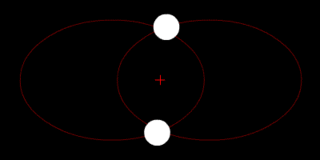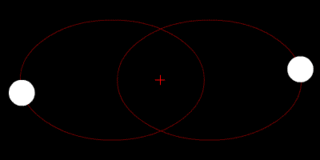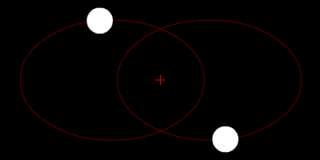Dos cuerpos con masa similar en órbita alrededor de un baricentro común con órbitas elípticas (una situación común para las estrellas binarias )

Localizar el centro de masa de una forma física 2D arbitraria

Este método es útil cuando se desea encontrar el centro de gravedad de un objeto plano complejo con dimensiones desconocidas.


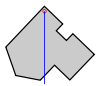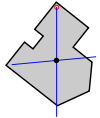Paso 1: Una forma 2D arbitraria.	Paso 2: Suspender la forma desde una ubicación cerca de un borde. Caída de un plomada y marca en el objeto.	Paso 3: Suspender la forma desde otra ubicación no demasiado cerca del primero. Caída de una plomada de nuevo y marcar. La intersección de las dos líneas es el centro de gravedad.

Localización de centro de masa

Este es un método de determinar el centro de masa de un objeto en forma de L.

CG del objeto en forma de L

Divide la forma en dos rectángulos, como se muestra en la figura 2. Encontrar el centro de masas de estos dos rectángulos trazando las diagonales. Dibuja una línea que une el centro de masas. El centro de masa de la forma debe estar en esta línea AB.
Divide la forma en otros dos rectángulos, como se muestra en la figura 3. Encontrar el centro de masas de estos dos rectángulos trazando las diagonales. Dibuja una línea que une el centro de masas. El centro de gravedad de la forma de L debe estar en esta línea CD.
A medida que el centro de masa de la forma debe encuentran a lo largo AB y también a lo largo de CD, es obvio que es en la intersección de estas dos líneas, en O. El punto O no podría estar dentro del objeto en forma de L.

Localizar el centro de masa de una forma compuesta

Este método es útil cuando se desea conocer el centro de gravedad de un objeto que se puede dividir fácilmente en formas primarias, cuyos centros de masa son fáciles de encontrar (ver Lista de centroides). Sólo nos estaremos encontrando el centro de masa en la dirección x aquí. El mismo procedimiento puede ser seguido para localizar el centro de la masa en la dirección y.

COG 1.svg La forma. Fácilmente se divide en un cuadrado, triángulo y círculo. Tenga en cuenta que el círculo tendrá un área negativa.

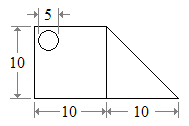COG 2.png Desde el Lista de los centroides, observamos las coordenadas de los centroides individuales.

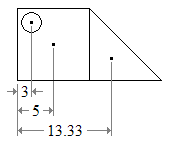COG 3.png De la ecuación 1 anterior: 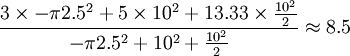$\ frac {\ 3 veces - \ pi2.5 ^ 2 + 5 \ épocas 10 ^ 2 + 13,33 \ times \ frac {10 ^ 2} {2}} {- \ pi2.5 ^ 2 + 10 ^ 2 + \ frac {10 ^ 2} {2}} \ aprox 8.5$ unidades.

El centro de masa de esta figura es a una distancia de 8,5 unidades de la esquina izquierda de la figura.

Localizar el centro de masa mediante el trazado alrededor del perímetro de la forma

Un desarrollo directo de la Planimeter conocido como un Integraph, o integerometer, se puede utilizar para establecer la posición del centro de masa de una forma irregular. Un término mejor es probablemente momento planímetro. Este método se puede aplicar a una forma con un contorno irregular, lisa o complejo donde otros métodos son demasiado difíciles. Fue utilizado regularmente por los constructores de barcos para garantizar que el buque no sería volcar. Ver Localizar el centro de la masa por medios mecánicos.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Center_of_mass&oldid=206108460 "