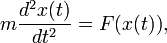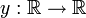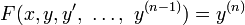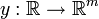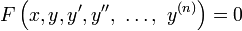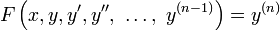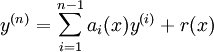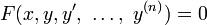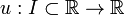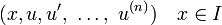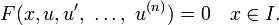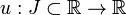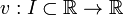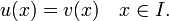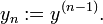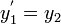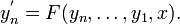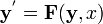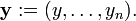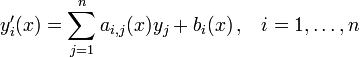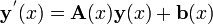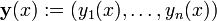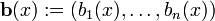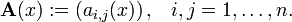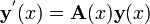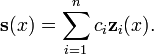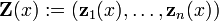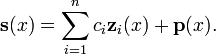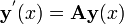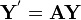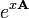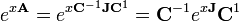Ecuaci??n diferencial ordinaria

Temas relacionados: Matem??ticas

Acerca de este escuelas selecci??n Wikipedia

Este contenido de Wikipedia ha sido seleccionada por SOS para su utilizaci??n en las escuelas de todo el mundo. Apadrina un ni??o para hacer una diferencia real.

En matem??ticas , una ecuaci??n diferencial ordinaria (o ODE) es una relaci??n que contiene las funciones de un solo variable independiente, y uno o m??s de sus derivados con respecto a esa variable.

Un ejemplo sencillo es la segunda ley de Newton del movimiento, lo que conduce a la ecuaci??n diferencial

$m \ frac {d ^ 2 x (t)} {dt ^ 2} = F (x (t)), \,$

para el movimiento de una part??cula de masa m. En general, la fuerza F depende de la posici??n de la part??cula x (t) en el tiempo t, y por lo tanto la funci??n desconocida x (t) aparece en ambos lados de la ecuaci??n diferencial, como se indica en la notaci??n F (x (t )).

Ecuaciones diferenciales ordinarias se deben distinguirse de las ecuaciones diferenciales parciales en los que hay varias variables independientes que implican derivadas parciales.

Ecuaciones diferenciales ordinarias surgen en muchos contextos diferentes, incluyendo la geometr??a, la mec??nica, la astronom??a y modelos de poblaci??n. Muchos matem??ticos famosos han estudiado las ecuaciones diferenciales y contribuido al campo, incluyendo Newton , Leibniz , la Familia Bernoulli, Riccati, Clairaut, d'Alembert y Euler .

Mucho trabajo se ha dedicado a la soluci??n de ecuaciones diferenciales ordinarias. En el caso en el que la ecuaci??n es lineal, se puede resolver por m??todos anal??ticos. Desafortunadamente, la mayor??a de las ecuaciones diferenciales interesantes son no lineales y, con pocas excepciones, no se pueden resolver con exactitud. Soluciones aproximadas se llegaron a utilizar aproximaciones inform??ticos (ver num??ricas de ecuaciones diferenciales ordinarias).

La trayectoria de una proyectil lanzado desde una ca????n sigue una curva determinada por una ecuaci??n diferencial ordinaria que se deriva de la segunda ley de Newton.

Definiciones

Ecuaci??n diferencial ordinaria

Sea y una funci??n desconocida

$y: \ mathbb {R} \ a \ mathbb {R}$

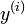en x con $y ^ {(i)}$ la i-??sima derivada de y, a continuaci??n, una funci??n de

$F (x, y, y ', \ \ dots, \ y ^ {(n-1)}) = y ^ {(n)}$

se llama una ecuaci??n diferencial ordinaria (ODE) de orden n. Para funciones vectoriales valorado

$y: \ mathbb {R} \ a \ mathbb {R} ^ m$

F se llama un sistema de ecuaciones diferenciales ordinarias de dimensi??n m.

Cuando una ecuaci??n diferencial de orden n tiene la forma

$F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n)} \ right) = 0$

se llama una ecuaci??n diferencial impl??cito mientras que la forma

$F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n-1)} \ right) = y ^ {(n)}$

se llama una ecuaci??n diferencial expl??cito.

Una ecuaci??n diferencial no en funci??n de x se llama aut??noma.

Una ecuaci??n diferencial se dice que es lineal si F puede escribirse como una combinaci??n lineal de los derivados de y

$y ^ {(n)} = \ sum_ {i = 1} ^ {n-1} a_i (x) y ^ {(i)} + r (x)$

con una _i (x) y r (x) funciones continuas en x. La funci??n r (x) se llama el t??rmino fuente; si r (x) = 0, entonces la ecuaci??n diferencial lineal se llama homog??nea, de lo contrario se llama no homog??nea o heterog??nea.

Soluciones

Dada una ecuaci??n diferencial

$F (x, y, y ', \ \ dots, \ y ^ {(n)}) = 0$

una funci??n

$u: I \ subset \ mathbb {R} \ a \ mathbb {R}$

se llama soluci??n o curva integral para F, si u es diferenciable n -los tiempos en I, F se define para todos

$(X, u, u ', \ \ dots, \ u ^ {(n)}) \ quad x \ in I$

$F (x, u, u ', \ \ dots, \ u ^ {(n)}) = 0 \ quad x \ in I.$

Dadas dos soluciones

$u: J \ subset \ mathbb {R} \ a \ mathbb {R}$

$v: I \ subset \ mathbb {R} \ a \ mathbb {R}$

u se llama una extensi??n de v si ⊂ J y

$u (x) = v (x) \ quad x \ in I. \,$

Una soluci??n que no tiene extensi??n se llama una soluci??n global.

Una soluci??n general de una ecuaci??n de orden n-??simo es una soluci??n que contiene 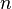$n$ las variables arbitrarias, correspondientes a n constantes de integraci??n. Una soluci??n particular se deriva de la soluci??n general mediante el establecimiento de las constantes a valores particulares, a menudo elegido para cumplir conjunto "Condiciones iniciales o de frontera. La soluci??n singular es una soluci??n que no se puede derivar de la soluci??n general.

Ejemplos

Reducci??n de un sistema de primer orden

Cualquier ecuaci??n diferencial de orden n puede escribirse como un sistema de ecuaciones diferenciales de primer orden n. Dada una ecuaci??n diferencial ordinaria expl??cita de orden n y la dimensi??n 1,

$F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n-1)} \ right) = y ^ {(n)}$

definimos una nueva familia de funciones desconocidas

$y_n: = y ^ {(n-1)} \.!$

A continuaci??n, podemos reescribir la ecuaci??n diferencial original como un sistema de ecuaciones diferenciales con orden 1 y dimensi??n n.

$y_1 ^ '= y_2$

$\ vdots$

$y_n ^ '= F (y_n, \ dots, y_1, x).$

que puede ser escrita de manera concisa en notaci??n vectorial como

$\ Mathbf {y} ^ '= \ mathbf {F} (\ mathbf {y}, x)$

con

$\ Mathbf {y}: = (y, \ ldots, y_n).$

Lineales de ecuaciones diferenciales ordinarias

Una clase particular bien entendido de las ecuaciones diferenciales son ecuaciones diferenciales lineales. Siempre podemos reducir una ecuaci??n diferencial lineal expl??cita de cualquier orden para un sistema de ecuaciones diferenciales de orden 1

$y_i '(x) = \ sum_ {j = 1} ^ n a_ {i, j} (x) y_j + b_i (x) \, \ mathrm {,} \ quad i = 1, \ ldots, n$

que se puede escribir de forma concisa utilizando notaci??n vectorial como

$\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)$

con

$\ Mathbf {y} (x): = (y_1 (x), \ ldots, y_n (x))$

$\ Mathbf {b} (x): = (b_1 (x), \ ldots, b_n (x))$

$\ Mathbf {A} (x): = (a_ {i, j} (x)) \, \ mathrm {,} \ quad i, j = 1, \ ldots, n.$

Ecuaciones homog??neas

El conjunto de soluciones de un sistema de ecuaciones diferenciales lineales homog??neas de orden 1 y dimensi??n n

$\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x)$

forma un n-dimensional espacio vectorial . Dada una base para este espacio vectorial 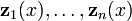$\ Mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x)$ , Que se llama un sistema fundamental, todas las soluciones 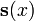$\ Mathbf {s} (x)$ puede ser escrito como

$\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} C_i \ mathbf {z} _i (x).$

La matriz n ?? n

$\ Mathbf {Z} (x): = (\ mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x))$

se llama matriz fundamental. En general no hay un m??todo para construir de forma expl??cita un sistema fundamental, pero si una soluci??n es conocida reducci??n de d'Alembert se puede utilizar para reducir la dimensi??n de la ecuaci??n diferencial por uno.

Ecuaciones no homog??neas

El conjunto de soluciones de un sistema de ecuaciones diferenciales lineales no homog??neas de orden 1 y dimensi??n n

$\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)$

puede ser construido por encontrar el sistema fundamental 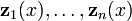$\ Mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x)$ a la correspondiente ecuaci??n homog??nea y una soluci??n particular 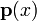$\ Mathbf {p} (x)$ a la ecuaci??n no homog??nea. Todas las soluciones 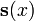$\ Mathbf {s} (x)$ con la ecuaci??n no homog??nea a continuaci??n, se puede escribir como

$\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} C_i \ mathbf {z} _i (x) + \ mathbf {p} (x).$

Una soluci??n particular de la ecuaci??n no homog??nea se puede encontrar por el m??todo de coeficientes indeterminados o la m??todo de variaci??n de par??metros.

Sistemas fundamentales para ecuaciones homog??neas con coeficientes constantes

Para un sistema homog??neo de ecuaciones diferenciales lineales con coeficientes constantes

$\ Mathbf {y} ^ '(x) = \ mathbf {A} \ mathbf {y} (x)$

podemos construir expl??citamente un sistema fundamental. El sistema se puede escribir como una ecuaci??n diferencial matricial

$\ Mathbf {Y} ^ '= \ mathbf {A} \ mathbf {Y}$

con una soluci??n como una matriz exponencial

$e ^ {x \ mathbf {A}}$

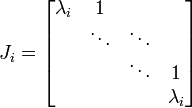
que es una matriz fundamental para la ecuaci??n diferencial inicial. Para calcular expl??citamente esta expresi??n nos transformamos en un Forma can??nica de Jordan

$e ^ {x \ mathbf {A}} = e ^ {x \ mathbf {C} ^ {- 1} \ mathbf {J} \ mathbf {C} ^ {1}} = \ mathbf {C} ^ {- 1 } e ^ {x \ mathbf {J}} \ mathbf {C} ^ {1}$

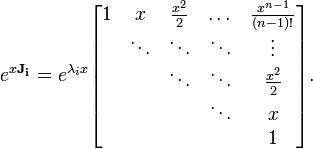
y luego evaluar la Bloques de Jordan

$J_i = \ begin {bmatrix} \ lambda_i & 1 & \; & \; \\ \; & \ Ddots & \ ddots & \; \\ \; & \; & \ Ddots & 1 \\ \; & \; & \; & \ Lambda_i \ end {bmatrix}$

de J por separado como

$e ^ {x \ mathbf {J_i}} = e ^ {\ lambda_i x} \ begin {bmatrix} 1 & x & \ frac {x ^ 2} {2} y \ dots & \ frac {x ^ {n-1 }} {(n-1)} \\ \!; & \ Ddots & \ ddots & \ ddots & \ vdots \\ \; & \; & \ Ddots & \ ddots & \ frac {x ^ 2} {2} \\ \; & \; & \; & \ Ddots y x \\ \; & \; & \; & \; & 1 \ end {bmatrix}.$

Las teor??as de la EDO

Soluciones singulares

La teor??a de la soluciones singulares de ecuaciones diferenciales ordinarias y parciales fue un tema de investigaci??n desde el momento de Leibniz, pero s??lo a partir de mediados del siglo XIX tuvieron que recibir atenci??n especial. Una obra valiosa pero poco conocido sobre el tema es el de Houtain (1854). Darboux (comenzando en 1873) era un l??der en la teor??a y en la interpretaci??n geom??trica de estas soluciones se abri?? un campo que fue trabajado por varios escritores, notablemente Casorati y Cayley. Para esta ??ltima se debe (1872) la teor??a de soluciones singulares de ecuaciones diferenciales de primer orden que acept?? circa 1900.

Reducci??n de cuadraturas

El intento primitivo en el tratamiento de las ecuaciones diferenciales tuvo a la vista una reducci??n de cuadraturas. Tal como hab??a sido la esperanza de algebristas del siglo XVIII para encontrar un m??todo para resolver la ecuaci??n general de la 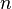$n$ ?? grado, por lo que era la esperanza de los analistas de encontrar un m??todo general para la integraci??n de cualquier ecuaci??n diferencial. Gauss (1799) mostr??, sin embargo, que la ecuaci??n diferencial cumple sus limitaciones muy pronto a menos que los n??meros complejos se introducen. De ah?? que los analistas comenzaron a sustituir el estudio de funciones, abriendo as?? un campo nuevo y f??rtil. Cauchy fue el primero en apreciar la importancia de este punto de vista. A partir de entonces la verdadera pregunta era ser, no si una soluci??n es posible por medio de funciones conocidas, o las integrales, pero si una ecuaci??n diferencial dada es suficiente para la definici??n de una funci??n de la variable o las variables independientes, y si es as??, ??cu??les son las propiedades caracter??sticas de esta funci??n.

Teor??a Fuchsian

Dos memorias de Fuchs (Crelle, 1866, 1868), inspirado en un enfoque novedoso, posteriormente elaborado por Thom?? y Frobenius. Collet fue un contribuyente importante a partir de 1869, aunque su m??todo para la integraci??n de un sistema no lineal se comunic?? a Bertrand en 1868. Clebsch (1873) atac?? la teor??a a lo largo de l??neas paralelas a las seguidas en su teor??a de la Integrales abelianas. Como este ??ltimo puede ser clasificado de acuerdo con las propiedades de la curva fundamental que permanece sin cambios en una transformaci??n racional, de modo Clebsch propuso clasificar las funciones trascendentes definidos por las ecuaciones diferenciales de acuerdo con las propiedades invariantes de las superficies correspondientes f = 0 bajo un racional -a-uno transformaciones.

La teor??a de Lie

Desde 1870 El trabajo de Lie puso la teor??a de ecuaciones diferenciales en un fundamento m??s satisfactorio. Demostr?? que las teor??as de la integraci??n de los matem??ticos m??s viejos puede, por la introducci??n de lo que ahora se llaman Grupos de Lie, ser referidos a una fuente com??n; y que las ecuaciones diferenciales ordinarias que admiten la misma transformaciones infinitesimales presentan dificultades comparables de integraci??n. Tambi??n hizo hincapi?? en el tema de la transformaciones de contacto (Ber??hrungstransformationen).

Teor??a de Sturm-Liouville

Teor??a de Sturm-Liouville es un m??todo general para la resoluci??n de ecuaciones de segundo orden lineales con coeficientes variables.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Ordinary_differential_equation&oldid=198824413 "