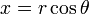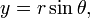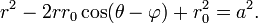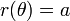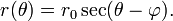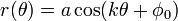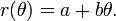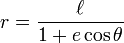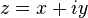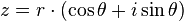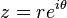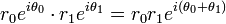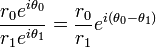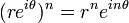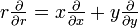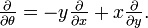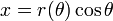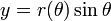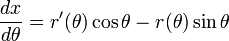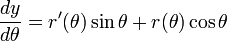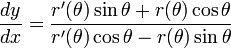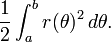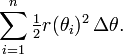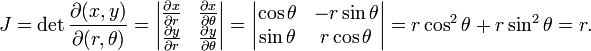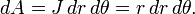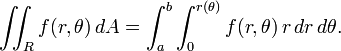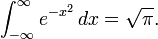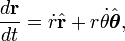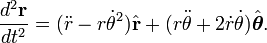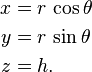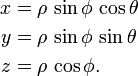Sistema de coordenadas polares
Sabías ...
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...
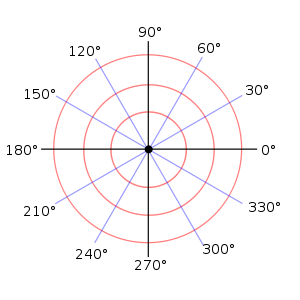
En matemáticas , el sistema de coordenadas polares es un bidimensional sistema en el que cada coordenada punto en un plano se determina por un ángulo y una distancia . El sistema de coordenadas polares es especialmente útil en situaciones en las que la relación entre dos puntos se expresa más fácilmente en términos de ángulos y la distancia; en el más familiar cartesiano sistema o coordenadas rectangulares, tal relación sólo puede encontrarse a través trigonométricas fórmulas.
Como el sistema de coordenadas es bidimensional, cada punto se determina mediante dos coordenadas polares: la coordenada radial y coordinar el angular. La coordenada radial (por lo general denota como  ) Indica la distancia a la punto de un punto central conocido como el polo (equivalente al origen en el sistema cartesiano). La coordenada angular (también conocido como el ángulo polar o la ángulo de acimut, y por lo general denotado por θ o
) Indica la distancia a la punto de un punto central conocido como el polo (equivalente al origen en el sistema cartesiano). La coordenada angular (también conocido como el ángulo polar o la ángulo de acimut, y por lo general denotado por θ o 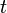 ) Denota la positiva o hacia la izquierda (en sentido antihorario) ángulo requerido para alcanzar el punto desde el 0 ° ray o eje polar (que es equivalente a la positiva del eje X en el plano de coordenadas cartesiano).
) Denota la positiva o hacia la izquierda (en sentido antihorario) ángulo requerido para alcanzar el punto desde el 0 ° ray o eje polar (que es equivalente a la positiva del eje X en el plano de coordenadas cartesiano).
Historia
Los conceptos de ángulo y radio ya fueron utilizados por los pueblos antiguos de la primera milenio BCE. La astrónomo Hiparco (190-120 aC) crea una tabla de funciones de acordes que dan la longitud de la cuerda para cada ángulo, y hay referencias a su uso de coordenadas polares en el establecimiento de posiciones estelares. En Sobre las espirales, Arquímedes describe el Espiral de Arquímedes, una función cuyo radio depende del ángulo. La palabra griega, sin embargo, no se extiende a un sistema de coordenadas completo.
Hay varias cuentas de la introducción de coordenadas polares como parte de un sistema formal de coordenadas. La historia completa de la asignatura se describe en Profesor de Harvard Origen de Julian Lowell Coolidge de coordenadas polares. Grégoire de Saint-Vincent y Bonaventura Cavalieri introdujo de forma independiente los conceptos en la mitad del siglo XVII. Saint-Vincent escribió sobre ellos en privado en 1625 y publicó su trabajo en 1647, mientras que Cavalieri publicó su en 1635 con una versión corregida que aparece en 1653. Cavalieri utilizó por primera vez las coordenadas polares para resolver un problema relacionado con el área dentro de un Espiral de Arquímedes. Blaise Pascal utiliza posteriormente coordenadas polares para calcular la longitud de arcos parabólicos.
En Método de las fluxiones (escrito 1671, publicado 1736), Sir Isaac Newton examinó las transformaciones entre coordenadas polares, que se refirió como la "manera Séptimo, porque Espirales", y otros nueve sistemas de coordenadas. En la revista Acta Eruditorum (1691), Jacob Bernoulli utilizar un sistema con un punto en una línea, llamado el polo y el eje polar respectivamente. Coordenadas fueron especificados por la distancia desde el polo y el ángulo desde el eje polar. El trabajo de Bernoulli extendió a la búsqueda de la radio de curvatura de las curvas expresadas en estas coordenadas.
El término real coordenadas polares se ha atribuido a Gregorio Fontana y fue utilizado por los escritores italianos del siglo 18o. El término apareció en Inglés en 1816 Traducción de George Peacock de De Cálculo Diferencial e Integral Lacroix. Alexis Clairaut fue el primero en pensar en coordenadas polares en tres dimensiones, y Leonhard Euler fue el primero en desarrollar realmente.
Trazado de puntos con coordenadas polares
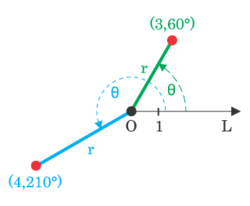
Cada punto en el sistema de coordenadas polares se puede describir con las dos coordenadas polares, que generalmente se llaman  (La coordenada radial) y θ (la coordenada angular, el ángulo polar, o ángulo de acimut, a veces representado como φ o
(La coordenada radial) y θ (la coordenada angular, el ángulo polar, o ángulo de acimut, a veces representado como φ o 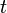 ). La
). La  coordinar representa la distancia radial desde el polo y el θ coordinar representa el ángulo en sentido antihorario (sentido antihorario) desde el 0 ° ray (a veces llamado el eje polar), conocido como el eje x positivo en el plano de coordenadas cartesiano .
coordinar representa la distancia radial desde el polo y el θ coordinar representa el ángulo en sentido antihorario (sentido antihorario) desde el 0 ° ray (a veces llamado el eje polar), conocido como el eje x positivo en el plano de coordenadas cartesiano .
Por ejemplo, las coordenadas polares (3, 60 °) sería trazada como un punto de 3 unidades desde el polo en el rayo 60 °. Las coordenadas (-3, 240 °) también se representan gráficamente en este punto porque una distancia radial negativo se mide como una distancia positiva en el rayo opuesto (el rayo reflejado sobre el origen, que difiere de la ray original de 180 °).
Un aspecto importante del sistema de coordenadas polares, no está presente en el sistema de coordenadas cartesianas, es que un solo punto se puede expresar con un número infinito de diferentes coordenadas. Esto es porque cualquier número de múltiples revoluciones puede hacerse alrededor del poste central sin afectar a la ubicación real del punto de trazado. En general, el punto (  , Θ) se puede representar como (
, Θ) se puede representar como (  , Θ ±
, Θ ± 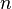 × 360 °) o (-
× 360 °) o (-  , Θ ± (2
, Θ ± (2 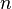 + 1) 180 °), donde
+ 1) 180 °), donde 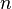 es cualquier número entero .
es cualquier número entero .
Las coordenadas arbitrarias (0, θ) se utilizan convencionalmente para representar el polo, como independientemente del θ de coordenadas, un punto con radio 0 siempre será en el poste. Para obtener una representación única de un punto, es habitual limitar  a los números no negativos
a los números no negativos  ≥ 0 y θ a la intervalo [0, 360 °) o (-180 °, 180 °] (o, en radianes, [0, 2π) o (-π, π]).
≥ 0 y θ a la intervalo [0, 360 °) o (-180 °, 180 °] (o, en radianes, [0, 2π) o (-π, π]).
Ángulos en notación polar se expresan generalmente en grados o radianes , usando la conversión 2 π rad = 360 °. La elección depende en gran medida del contexto. Las aplicaciones de navegación utilizan medida en grados, mientras que algunos de física (mecánica aplicaciones específicamente de rotación) y casi toda la literatura matemática de cálculo utilizan radianes.
La conversión entre coordenadas cartesianas y polares

Las dos coordenadas polares  y θ se pueden convertir a las coordenadas cartesianas
y θ se pueden convertir a las coordenadas cartesianas 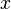 y
y 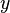 mediante el uso de la funciones trigonométricas seno y coseno:
mediante el uso de la funciones trigonométricas seno y coseno:
mientras que las dos coordenadas cartesianas 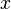 y
y 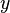 se puede convertir en coordenadas polares
se puede convertir en coordenadas polares  por
por
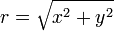 (Por una simple aplicación del teorema de Pitágoras ).
(Por una simple aplicación del teorema de Pitágoras ).
Para determinar la coordenada angular θ, las dos ideas siguientes deben ser considerados:
- Para
 = 0, θ puede ajustarse a cualquier valor real .
= 0, θ puede ajustarse a cualquier valor real . - Para
 ≠ 0, para obtener una representación única para θ, debe limitarse a un intervalo de tamaño 2π. Opciones convencionales para tal intervalo son [0, 2π) y (-π, π].
≠ 0, para obtener una representación única para θ, debe limitarse a un intervalo de tamaño 2π. Opciones convencionales para tal intervalo son [0, 2π) y (-π, π].
Para obtener θ en el intervalo [0, 2π), lo siguiente puede ser utilizado ( 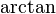 denota la inversa de la tangente función):
denota la inversa de la tangente función):
Para obtener θ en el intervalo (-π, π], lo siguiente puede ser utilizado:
Uno puede evitar tener que llevar un registro de los signos de numerador y denominador por el uso de la atan2 función, que tiene argumentos separados para el numerador y el denominador.
Ecuaciones polares
La ecuación que define una curva algebraica expresada en coordenadas polares se conoce como una ecuación polar. En muchos casos, una ecuación tal simplemente se puede especificar mediante la definición  como una función de θ. La curva resultante se compone de puntos de la forma (
como una función de θ. La curva resultante se compone de puntos de la forma (  (Θ), θ) y puede ser considerado como el gráfica de la función polar
(Θ), θ) y puede ser considerado como el gráfica de la función polar  .
.
Diferentes formas de simetría pueden deducirse de la ecuación de una función polar  . Si
. Si  (-θ) =
(-θ) =  (Θ) de la curva será simétrica con respecto a la horizontal (0 ° / 180 °) ray, si
(Θ) de la curva será simétrica con respecto a la horizontal (0 ° / 180 °) ray, si  (Π-θ) =
(Π-θ) =  (Θ) será simétrica con respecto al rayo (90 ° / 270 °) vertical, y si
(Θ) será simétrica con respecto al rayo (90 ° / 270 °) vertical, y si  (Θ-α °) =
(Θ-α °) =  (Θ) será ° α con simetría de rotación en sentido antihorario alrededor del polo.
(Θ) será ° α con simetría de rotación en sentido antihorario alrededor del polo.
Debido a la naturaleza circular del sistema de coordenadas polar, muchas curvas pueden ser descritos por una ecuación polar bastante simple, mientras que su forma cartesiana es mucho más compleja. Entre los más conocidos de estas curvas son la Polar Rose, Espiral de Arquímedes, lemniscata, limaçon, y cardioide.
Para el círculo, la línea y la rosa polar continuación, se entiende que no existen restricciones sobre el dominio y el rango de la curva.
Círculo

 (Θ) = 1
(Θ) = 1 La ecuación general para un círculo con un centro en (  0, φ) y el radio
0, φ) y el radio 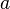 es
es
Esto se puede simplificar de varias maneras, para ajustarse a los casos más específicos, tales como la ecuación
para un círculo con un centro en el polo y el radio 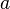 .
.
Línea
Líneas radiales (aquellas que atraviesa el polo) están representados por la ecuación
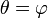 ,
,
donde φ es el ángulo de elevación de la línea; es decir, φ = arctan 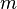 donde
donde 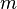 es el pendiente de la línea en el sistema de coordenadas cartesiano. La línea no radial que cruza la línea radial θ = φ perpendicularmente en el punto (
es el pendiente de la línea en el sistema de coordenadas cartesiano. La línea no radial que cruza la línea radial θ = φ perpendicularmente en el punto (  0, φ) tiene la ecuación
0, φ) tiene la ecuación
Polar Rose

 (Θ) = 2 sen 4θ
(Θ) = 2 sen 4θ La rosa polar es una famosa curva matemática que se parece a una flor de pétalos, y que puede expresarse como una ecuación polar simple,
para cualquier constante 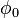 (Incluyendo 0). Si k es un número entero, estas ecuaciones se producen una k -petalled Rose Si k es extraño, o un 2 k -petalled aumentó si k es par. Si k es racional, pero no es un entero, una forma de rosa como se puede formar pero con pétalos superpuestos. Tenga en cuenta que estas ecuaciones no definen una rosa con 2, 6, 10, 14, etc. pétalos. La una variable representa la longitud de los pétalos de la rosa.
(Incluyendo 0). Si k es un número entero, estas ecuaciones se producen una k -petalled Rose Si k es extraño, o un 2 k -petalled aumentó si k es par. Si k es racional, pero no es un entero, una forma de rosa como se puede formar pero con pétalos superpuestos. Tenga en cuenta que estas ecuaciones no definen una rosa con 2, 6, 10, 14, etc. pétalos. La una variable representa la longitud de los pétalos de la rosa.
Espiral de Arquímedes
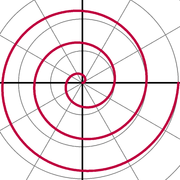
La Espiral de Arquímedes es un famoso espiral que fue descubierta por Arquímedes , que también se puede expresar como una ecuación polar simple. Se representa por la ecuación
Cambiar el parámetro a su vez, la espiral, mientras que b controla la distancia entre los brazos, que por una espiral dada es siempre constante. La espiral de Arquímedes tiene dos brazos, uno para θ> 0 y otro para θ <0. Los dos brazos están conectados sin problemas en el polo. Tomando la imagen de espejo de un brazo a través de la línea ° 90 ° / 270 producirá el otro brazo. Esta curva es notable como una de las primeras curvas, después de que las secciones cónicas , que se describirá en un tratado matemático, y como un ejemplo de una curva que se define mejor por una ecuación polar.
Las secciones cónicas
Una sección cónica con un foco en el poste y el otro en algún lugar del rayo 0 ° (de modo que de la cónica eje mayor yace a lo largo del eje polar) viene dada por:
donde e es la excentricidad y 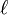 es el recto semi-latus (la distancia perpendicular en un foco desde el eje principal de la curva). Si e> 1, esta ecuación define una hipérbola; si e = 1, que define una parábola; y si e <1, define una elipse . El caso especial e = 0 de los últimos resultados en un círculo de radio
es el recto semi-latus (la distancia perpendicular en un foco desde el eje principal de la curva). Si e> 1, esta ecuación define una hipérbola; si e = 1, que define una parábola; y si e <1, define una elipse . El caso especial e = 0 de los últimos resultados en un círculo de radio 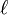 .
.
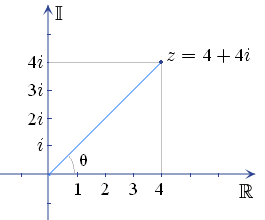
Los números complejos
Cada número complejo se puede representar como un punto en el plano complejo , y por lo tanto se puede expresar mediante la especificación de cualquiera de las coordenadas del punto cartesianas (llamados forma rectangular o cartesiano) o coordenadas polares es el punto (llamado forma polar). El número complejo z se puede representar en forma rectangular como se
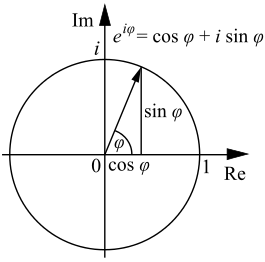
donde i es la unidad imaginaria , o, alternativamente, se puede escribir en forma polar (a través de las fórmulas de conversión indicados anteriormente ) como
y desde allí como
donde e es El número de Euler, que son equivalentes como se muestra por La fórmula de Euler. (Tenga en cuenta que esta fórmula, como todos los que implican exponenciales de los ángulos, se supone que el ángulo θ se expresa en radianes.) Para convertir entre las formas rectangulares y polares de un número complejo, las fórmulas de conversión dadas anteriormente pueden ser utilizados.
Para las operaciones de multiplicación , división y exponenciación de números complejos, por lo general es mucho más sencillo trabajar con números complejos expresados en forma polar en vez de forma rectangular. A partir de las leyes de la exponenciación:
- Multiplicación:
- División:
- Exponenciación ( Fórmula de De Moivre):
Cálculo
Cálculo se puede aplicar a ecuaciones expresadas en coordenadas polares.
La coordenada angular θ se expresa en radianes largo de esta sección, que es la elección convencional al hacer el cálculo.
Cálculo diferencial
Contamos con las siguientes fórmulas:
Para encontrar la pendiente cartesiana de la recta tangente a una curva r polar (θ) en un momento dado, la curva se expresa por primera vez como un sistema de ecuaciones paramétricas.
Diferenciación de ambas ecuaciones con respecto a los rendimientos θ
Dividiendo la segunda ecuación por el primero rendimientos de la pendiente cartesiana de la recta tangente a la curva en el punto (r, r (θ)):
Cálculo integral
Sea R denota la región encerrada por una curva r (θ) y los rayos θ = a y θ = b, donde 0 <b - a <2π. Entonces, el área de R es
Este resultado se puede encontrar como sigue. En primer lugar, el intervalo [a, b] se divide en n subintervalos, donde n es un número entero positivo arbitrario. Así Δθ, la longitud de cada subintervalo, es igual a b - a (la longitud total del intervalo), dividido por n, el número de subintervalos. Para cada subintervalo i = 1, 2, ..., n, sea θ i ser el punto medio del subintervalo, y construir un sector con el centro en el polo, el radio r (θ i), ángulo central Δθ y longitud de arco 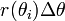 . El área de cada sector construida es por lo tanto igual a
. El área de cada sector construida es por lo tanto igual a 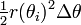 . Por lo tanto, el área total de todos los sectores es
. Por lo tanto, el área total de todos los sectores es
A medida que aumenta el número de subintervalos n, la aproximación de la zona sigue mejorando. En el límite, cuando n → ∞, la suma se convierte en el Suma de Riemann para la integral anterior.
Generalización
Usando coordenadas cartesianas , un elemento de área infinitesimal se puede calcular como dA = dx dy. La regla de sustitución para integrales múltiples establece que, cuando se utilizan otras coordenadas, los Jacobiano de la fórmula conversión de coordenadas tiene que ser considerado:
Por lo tanto, un elemento de área en coordenadas polares se puede escribir como
Ahora, una función que se le da en coordenadas polares se puede integrar como sigue:
Aquí, R es la misma región que anteriormente, a saber, la región encerrada por una curva r (θ) y los rayos θ = a y θ = b.
La fórmula para el área de I mencionado anteriormente se recupera tomando f idénticamente igual a 1. A más sorprendente aplicación de este resultado se obtiene el Integral de Gauss
Cálculo vectorial
Cálculo vectorial también se puede aplicar a coordenadas polares. Dejar 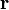 ser el vector de posición
ser el vector de posición 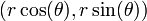 , Con R y
, Con R y 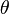 en función del tiempo t,
en función del tiempo t, 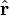 ser un vector unitario en la dirección
ser un vector unitario en la dirección 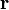 y
y 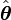 ser un vector unidad en ángulo recto con
ser un vector unidad en ángulo recto con 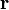 . Las primera y segunda derivadas de la posición son
. Las primera y segunda derivadas de la posición son
Tres dimensiones
El sistema de coordenadas polares se extiende en tres dimensiones con dos sistemas de coordenadas diferentes, el cilíndrica y sistemas de coordenadas esféricas, ambos de los cuales incluyen dos dimensiones coordenadas polares o planares como un subconjunto. En esencia, la coordenada cilíndrica sistema de coordenadas polares se extiende mediante la adición de una distancia adicional de coordenadas, mientras que el sistema esférico en lugar agrega un adicional de coordenada angular.
Coordenadas cilíndricas
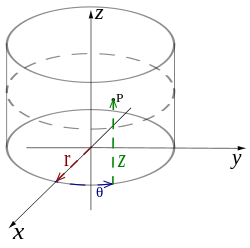
El sistema cilíndrico de coordenadas es un sistema de coordenadas que se extiende esencialmente el de dos dimensiones del sistema de coordenadas polares por la adición de una tercera coordenada medir la altura de un punto por encima del plano, similar a la manera en la que el sistema de coordenadas cartesianas se extiende en tres dimensiones. La tercera coordenada se denota generalmente h, por lo que las tres coordenadas cilíndricas (r, θ, h).
Las tres coordenadas cilíndricas se pueden convertir a coordenadas cartesianas por
Coordenadas esféricas
Las coordenadas polares también se pueden extender en tres dimensiones utilizando las coordenadas (ρ, φ, θ), donde ρ es la distancia desde el origen, φ es el ángulo desde el eje z (llamado el colatitud o cenit y se mide de 0 a 180 °) y θ es el ángulo desde el eje x (como en las coordenadas polares). Este sistema de coordenadas, llamado el sistema de coordenadas esféricas, es similar a la latitud y sistema de longitud utilizado para la Tierra, con el origen en el centro de la Tierra, la latitud δ siendo el complemento de φ, determinado por δ = 90 ° - φ, y la longitud l que se mide por L = θ - 180 °.
Las tres coordenadas esféricas se convierten en coordenadas cartesianas por
Aplicaciones
Las coordenadas polares son de dos dimensiones y por lo tanto se pueden usar sólo cuando posiciones de los puntos se encuentran en un único plano de dos dimensiones. Ellos son los más apropiados en cualquier contexto donde el fenómeno considerado es intrínsecamente ligado a la dirección y longitud de un punto central. Por ejemplo, los ejemplos anteriores muestran cómo las ecuaciones polares elementales son suficientes para definir curvas - como la espiral de Arquímedes - cuya ecuación en el sistema de coordenadas cartesianas serían mucho más intrincado. Por otra parte, muchos sistemas físicos - tales como los relacionados con los cuerpos en movimiento alrededor de un punto central o con fenómenos se originan en un punto central - son más simples y más intuitiva para modelar utilizando coordenadas polares. La motivación inicial para la introducción del sistema polar fue el estudio de circular y movimiento orbital.
Las coordenadas polares se utilizan a menudo en navegación, como el destino o dirección de desplazamiento se pueden dar como un ángulo y distancia del objeto que está siendo considerado. Por ejemplo, las aeronaves usar una versión ligeramente modificada de las coordenadas polares para la navegación. En este sistema, la que se utiliza generalmente para cualquier tipo de navegación, el rayo 0 ° se denomina generalmente la partida 360, y los ángulos de continuar en una dirección a la derecha, en lugar de en sentido antihorario, como en el sistema matemático. La partida 360 corresponde a norte magnético, mientras que las partidas 90, 180 y 270 corresponden a este magnético, sur y oeste, respectivamente. Por lo tanto, un avión que viaja 5 millas náuticas al este estará viajando 5 unidades a la partida 90 (leer niner-cero control de tráfico aéreo).
Modelado
Sistemas de imagen simetría radial proporcionar escenarios naturales para el sistema de coordenadas polares, con la actuación como punto central el polo. Un buen ejemplo de este uso es el ecuación de flujo de las aguas subterráneas cuando se aplica a los pozos radialmente simétricos. Los sistemas con una fuerza radial también son buenos candidatos para el uso del sistema de coordenadas polar. Estos sistemas incluyen los campos gravitatorios , que obedecen a la la ley del cuadrado inverso, así como sistemas con fuentes puntuales, tales como antenas de radio.
Radialmente sistemas asimétricos también pueden ser modelados con coordenadas polares. Por ejemplo, una micrófono del patrón de captación ilustra su respuesta proporcional a un sonido entrante desde una dirección dada, y estos patrones se puede representar como curvas polares. La curva para un micrófono cardioide estándar, el micrófono unidireccional más común, se puede representar como θ r = 0,5 + 0,5 pecado.