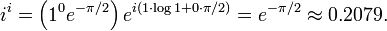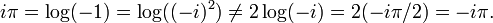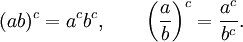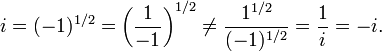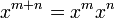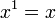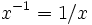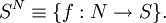Exponenciaci??n
Antecedentes
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organiz?? esta selecci??n. Haga clic aqu?? para obtener m??s informaci??n sobre SOS Children.
Exponenciaci??n es un matem??tico operaci??n, escrito a n, que involucra a dos n??meros, los base de una y el exponente n. Cuando n es un positivo entero , exponenciaci??n corresponde a repetirse la multiplicaci??n :
al igual que la multiplicaci??n por un n??mero entero corresponde a repetida adem??s :
El exponente es generalmente muestra como una super??ndice a la derecha de la base. La exponenciaci??n a n puede leerse como: un elevado a la potencia n-??sima o un elevado a la potencia [de] n, o m??s brevemente: una a la potencia en??sima o al poder [de] n, o a??n m??s breve: una para el n. Algunos exponentes se pueden leer de una manera determinada; por ejemplo, un 2 suele leerse como un cuadrado y un 3 como un cubo.
La potencia de un n tambi??n se puede definir cuando el exponente n es un entero negativo. Cuando la base a es un n??mero real positivo, la potencia se define para exponentes reales e incluso complejos n. La especial funci??n exponencial e x es fundamental para esta definici??n. Permite a las funciones de la trigonometr??a para ser expresados por la exponenciaci??n. Sin embargo, cuando la base de un no es un n??mero real positivo y el exponente n no es un entero, entonces un n no puede ser definido como un ??nico funci??n continua de a.
Exponenciaci??n donde el exponente es una matriz se utiliza para sistemas de resolver ecuaciones diferenciales lineales.
Exponenciaci??n se utiliza penetrante en muchos otros campos, as??, como la econom??a, la biolog??a, la qu??mica, la f??sica y la inform??tica, con aplicaciones como inter??s compuesto, crecimiento de la poblaci??n, qu??micas cin??tica de la reacci??n, la onda comportamiento, y La criptograf??a de clave p??blica.
Exponenciaci??n con exponentes enteros
La operaci??n de exponenciaci??n con exponentes enteros s??lo requiere ??lgebra elemental .
Exponentes enteros positivos
2 = a ?? a se llama cuadrada de un puesto que el ??rea de un cuadrado de lado de longitud a es un 2.
un 3 = a ?? a ?? a se llama cubo, ya que el volumen de un cubo con lados de longitud a es un 3.
As?? que 3 2 se dice "tres al cuadrado", y 2 3 es "dos cubos".
El exponente dice c??mo se multiplican entre s?? muchas copias de la base. Por ejemplo, 3 5 = 3 ?? 3 ?? 3 ?? 3 ?? 3 = 243. La base 3 aparece 5 veces en la multiplicaci??n repetida, ya que el exponente es 5. Aqu??, 3 es la base, 5 es el exponente, y 243 es la potencia o, m??s espec??ficamente, la quinta potencia de 3 o 3 elevado a la quinta potencia.
La palabra "levantado" por lo general se omite, y m??s a menudo "poder" y, por lo 3 5 es t??picamente pronunciado "tres al quinto" o "tres de los cinco".
Formalmente, las potencias con exponentes enteros positivos pueden ser definidos por la condici??n inicial a 1 = a y la relaci??n de recurrencia a n 1 = a ?? a n.
Exponentes de uno y cero
Observe que 3 1 es el producto de un solo 3, que es evidentemente 3.
Tambi??n tenga en cuenta que el 3 5 = 3 ?? 3 4. Tambi??n 3 4 = 3 ?? 3 3. Siguiendo esta tendencia, que deber??a tener
- 3 1 = 3 ?? 3 0.
Otra forma de decir esto es que cuando n, m, y n - m son positivos (y si x no es igual a cero), se puede ver contando el n??mero de ocurrencias de x que
Extensi??n al caso de que n y m son iguales, la ecuaci??n ser??a leer
ya que tanto el numerador y el denominador son iguales. Por lo tanto tomamos esto como la definici??n de x 0.
Por lo tanto definimos 3 0 = 1, de modo que la igualdad anterior se mantiene. Esto nos lleva a la siguiente regla:
- Cualquier n??mero a la potencia 1 es en s?? misma.
- Cualquier n??mero distinto de cero a la potencia 0 es 1; una interpretaci??n de estos poderes es tan productos vac??os. Se discute el caso de 0 0 por debajo .
Interpretaci??n combinatoria
Para enteros no negativos n y m, la potencia n m es igual a la cardinalidad del conjunto de m - tuplas de una n -element set, o el n??mero de palabras m -Carta de un n -Carta alfabeto.
- 0 5 = | {} | = 0. No hay un 5-tupla del conjunto vac??o.
- 1 4 = | {(1,1,1,1)} | = 1. Hay una 4-tupla de un conjunto de un solo elemento.
- 2 3 = | {(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1, 2), (2,2,1), (2,2,2)} | = 8. Hay 8 3-adas de un conjunto de dos elementos.
- 3 2 = | {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3, 2), (3,3)} | = 9. Hay 9 2-tuplas de un conjunto de tres elementos.
- 4 1 = | {(1), (2), (3), (4)} | = 4. Hay 4 1-tuplas de un conjunto de cuatro elementos.
- 5 0 = | {()} | = 1. Hay exactamente un vac??o tupla.
Ver tambi??n exponenciaci??n sobre conjuntos .
Exponentes enteros negativos
Criar a un n??mero distinto de cero a la potencia -1 produce su rec??proco.
Por lo tanto:
El aumento de 0 a una potencia negativa implicar??a divisi??n por 0, y as?? no est?? definido.
Un exponente entero negativo tambi??n puede ser visto como repetida divisi??n por la base. As??  .
.
Identidades y propiedades
El m??s importante identidad satisfecha por la exponenciaci??n entero es:
Esta identidad tiene como consecuencia:
para a ≠ 0, y
 .
.
Otra identidad b??sica es
 .
.
Mientras que la suma y la multiplicaci??n son conmutativa (por ejemplo, 2 + 3 = 5 = 3 + 2 y 2 ?? 3 = 6 = 3 ?? 2), exponenciaci??n no es conmutativo: 2 3 = 8, pero 3 2 = 9.
Del mismo modo, mientras que la adici??n y la multiplicaci??n son asociativo (por ejemplo, (2 + 3) 4 = 9 = 2 + (3 + 4) y (2 ?? 3) ?? 4 = 24 = 2 ?? (3 ?? 4), la exponenciaci??n es no asociativas ya sea: 2 3 para el cuarto poder es 8 4 ?? 4096, pero 2 a la potencia 3 4 es 2 81 o 2.417.851.639.229.258.349.412.352 Sin par??ntesis para modificar el orden de c??lculo, el orden se entiende generalmente para ser de derecha a izquierda.:
Potencias de diez
- Ver Notaci??n cientifica
Potencias de 10 son f??cilmente computado en la base diez ( decimal sistema num??rico). Por ejemplo, 10 8 = 100000000.
Exponenciaci??n con la base 10 se utiliza en notaci??n cient??fica para describir n??meros grandes o peque??os. Por ejemplo, 299792458 (la velocidad de la luz en el vac??o, en metros por segundo) se puede escribir como 2.99792458 ?? 10 8 y luego aproximar como 2,998 ?? 10 8, (o, a veces como 299,8 ?? 10 6 o 299.8E + 6, sobre todo en los programas inform??ticos).
Prefijos SI basados en potencias de 10 tambi??n se utilizan para describir cantidades peque??as o grandes. Por ejemplo, el prefijo kilo significa 10 3 = 1.000, por lo que un kil??metro es 1000 metros.
Poderes de dos
El positivo potencias de 2 son importantes en la ciencia de la computaci??n , porque hay 2 n posibles valores para un n - bit variable. Ver sistema de numeraci??n binario .
Potencias de 2 son importantes en la teor??a de conjuntos desde un conjunto con n elementos tiene un el poder establecido, o conjunto de todos los subconjuntos del conjunto original, con 2 n miembros.
Las potencias negativas de 2 se utiliza com??nmente, y los dos primeros tienen nombres especiales: medio, y trimestre.
Poderes de uno
Las potencias enteras de uno son uno: 1 n = 1.
Poderes de cero
Si el exponente es positivo, el poder de cero es cero: 0 n = 0, donde n> 0.
Si el exponente es negativo, el poder de cero (0 - n, donde n> 0) permanece indefinida, debido a la divisi??n por cero est?? impl??cita.
Si el exponente es cero, algunos autores definen 0 0 = 1, mientras que otros lo dejan sin definir, como se discute a continuaci??n .
Poderes de menos uno
Los poderes de menos uno son ??tiles para expresar secuencias alternas.
Si el exponente es par, la potencia de menos uno es uno: (-1) 2 n = 1.
Si el exponente es impar, la potencia de menos uno es menos uno: (-1) 2 n 1 = -1.
Facultades de la unidad imaginaria
Las competencias de la unidad imaginaria i son ??tiles para expresar secuencias de per??odo 4. Ver, por ejemplo, Ra??z de la unidad # Periodicidad.
Potencias de e
El n??mero e, la base de la logaritmo natural , es un bien estudiado constante aproximadamente igual a 2,718. Se puede aproximar por grandes potencias positivas o negativas de los n??meros cercanos a uno, como
o
y se define como la l??mite
Cualquier fuente de entero no nulo de correo se puede calcular as??:
La funci??n exponencial , definida por
tiene aplicaciones en muchas ??reas de las matem??ticas y la ciencia. Esta definici??n de e x coincide con la definici??n de e k cuando x es un n??mero entero, pero tambi??n se aplica para los valores fraccionarios, reales o complejos de x, e incluso cuando x es una matriz cuadrada , que se utiliza en ecuaciones diferenciales ordinarias .
Otra f??rmula popular es la serie de potencias
 .
.
Potencias de n??meros reales
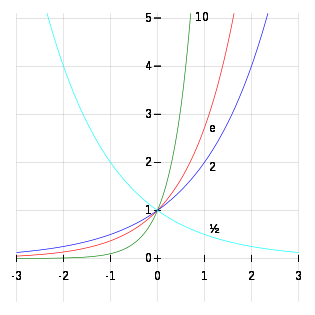
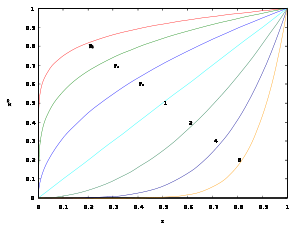
Criar a un n??mero real positivo a un poder que no es un n??mero entero que se puede lograr de dos maneras.
- N??mero racional exponentes pueden ser definidos en t??rminos de n-??simo ra??ces, y exponentes distintos de cero arbitrarias pueden ser definidos por la continuidad.
- El logaritmo natural se puede utilizar para definir exponentes reales utilizando la funci??n exponencial.
Las identidades y las propiedades que se muestran arriba son verdaderas para exponentes no enteros tambi??n.
Principal en??sima ra??z
Una ra??z en??sima de un n??mero a es un n??mero b tal que b n = a.
Cuando se hace referencia a la ra??z n-??sima de un n??mero real una se supone que lo que se desea es el principal ra??z en??sima del n??mero. Si a es un n??mero real, y n es un entero positivo, entonces la ??nica soluci??n real con el mismo signo como a la ecuaci??n
se llama el director n-??sima ra??z de un, y se denota ![\ Sqrt [n] {a}](../../images/114/11497.png) usando el radical s??mbolo
usando el radical s??mbolo  .
.
![x = a ^ {\ frac {1} {n}} = \ sqrt [n] {a}](../../images/114/11499.png) .
.
Por ejemplo: 4 1/2 = 2, 8 1/3 = 2, (-8) 1/3 = -2,.
Tenga en cuenta que si n es incluso, los n??meros negativos no tendr??n un n ?? director ra??z.
Facultades racionales de n??meros reales positivos
Exponenciaci??n con una racional exponente m / n puede definirse como
![a ^ {\ frac {m} {n}} = \ left (a ^ m \ right) ^ {\ frac {1} {n}} = \ sqrt [n] {a ^ m}](../../images/115/11500.png) .
.
Por ejemplo, 8 2/3 = 4.
Dado que cualquier n??mero real se puede aproximar por los n??meros racionales, exponenciaci??n a un arbitraria exponente k verdadero puede ser definido por continuidad con la regla
donde se toma el l??mite s??lo sobre los valores racionales de la r.
Por ejemplo, si
entonces
Poderes reales de los n??meros reales positivos
El logaritmo natural ln (x) es la inversa de la funci??n exponencial e x. Se define para cada n??mero real b positivo y satisface la ecuaci??n
Suponiendo b x ya est?? definido, las reglas de logaritmos y exponentes dan la igualdad
Esta igualdad se puede utilizar para definir la exponenciaci??n con cualquier base real positivo como b
Esta definici??n del n??mero real de energ??a b x est?? de acuerdo con la definici??n dada anteriormente usando exponentes racionales y continuidad. La definici??n de exponenciaci??n usando logaritmos es m??s com??n en el contexto de los n??meros complejos, como se discute a continuaci??n.
Algunas potencias racionales de n??meros reales negativos
Ni el m??todo de logaritmo ni el m??todo exponente fraccionario se pueden utilizar para definir una k como un n??mero real de un n??mero real negativo A y un n??mero real k arbitrario. En algunos casos especiales, una definici??n es posible: potencias enteras de n??meros reales negativos son los n??meros reales, y los poderes racionales de la forma a m / n, donde n es impar puede ser calculada usando ra??ces. Pero puesto que no hay un n??mero real x tal que x 2 = -1, la definici??n de un m / n cuando n es par y m es impar debe utilizar la unidad imaginaria i, como se describe con m??s detalle en la siguiente secci??n.
El m??todo logaritmo no se puede utilizar para definir una k como un n??mero real cuando un <0 porque e x es no negativo para cada n??mero real x, por lo que log (a) no puede ser un n??mero real.
El m??todo exponente racional no puede ser utilizado para valores negativos de un porque se basa en continuidad. La funci??n f (r) = a r tiene una extensi??n continua ??nica a partir de los n??meros racionales para los n??meros reales para cada a> 0. Pero cuando un <0, la funci??n f no es continua, incluso en el conjunto de los n??meros racionales r para el cual se define.
Por ejemplo, tomemos a = -1. La ra??z en??sima de -1 es -1 por cada impar n??mero natural n. As?? que si n es un entero positivo impar, (-1) (m / n) = -1 si m es impar, y (-1) (m / n) = 1 si m es par. As??, el conjunto de los n??meros racionales q para que -1 q = 1 es denso en los n??meros racionales, como es el conjunto de q para el que q = -1 -1. Esto significa que la funci??n (-1) q no es continua en cualquier n??mero racional q donde se define.
Poderes imaginarios de correo
La interpretaci??n geom??trica de las operaciones con n??meros complejos y la definici??n de poderes de correo es la clave para entender e i ?? x para x real. Considera el tri??ngulo rect??ngulo (0, 1, 1 + i ?? x / n). Para valores grandes de n del tri??ngulo es casi un sector circular con un peque??o ??ngulo central igual a x / n radianes. Los tri??ngulos (0, (1 + i ?? x / n) k, (1 + i ?? x / n) k 1) son mutuamente similar para todos los valores de k. As?? que para valores grandes de N el punto de (1+ ix / n) la limitaci??n de N es el punto de la unidad de c??rculo cuyo ??ngulo desde el eje real positivo es x radianes . Las coordenadas polares de este punto son (r, θ) = (1, x), y las coordenadas cartesianas son (cos (x), sin (x)). As?? E I ?? x = cos (x) + i ?? sen (x), y esto es La f??rmula de Euler, la conexi??n de ??lgebra a la trigonometr??a por medio de los n??meros complejos .
Las soluciones de la ecuaci??n e z = 1 son los m??ltiplos enteros de 2 ?? π ?? i:
M??s generalmente, si e b = a, entonces cada soluci??n a E z = A se puede obtener mediante la adici??n de un m??ltiplo entero de 2 ?? π ?? i a B:
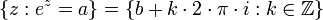 .
.
As??, la funci??n exponencial compleja es una funci??n peri??dica de per??odo 2 ?? π ?? i.
Funciones trigonom??tricas
Se deduce de La f??rmula de Euler que la funciones trigonom??tricas coseno y seno son
Hist??ricamente, coseno y seno se definen geom??tricamente antes de la invenci??n de los n??meros complejos. La f??rmula anterior reduce las complicadas f??rmulas para funciones trigonom??tricas de la suma en la f??rmula exponenciaci??n sencilla
Uso de exponenciaci??n con exponentes complejos uno no necesita estudiar trigonometr??a.
Poderes de los est??ndares e
El poder e x + i ?? y se calcula e x i ?? e ?? y. El factor real e x es el valor absoluto de x + e i ?? Y y el factor complejo e i ?? y la identifica direcci??n de e x + i ?? y.
Potencias complejas de n??meros reales positivos
Si a es un n??mero real positivo, y z es cualquier n??mero complejo, la potencia de una z se define como z e ?? ln (a), donde x = ln (a) es la ??nica soluci??n real a la ecuaci??n e x = a. As?? mismo m??todo de trabajo exponentes reales tambi??n funciona para los exponentes complejos. Por ejemplo:
- 2 i = e i ?? ln (2) = cos (ln (2)) + i ?? sen (ln (2)) = 0.7692+ i ?? 0.63896
- e i = 0.54030+ i ?? 0.84147
- 10 i = -0.66820+ i ?? 0.74398
- (E 2 ?? π) i = 535,49 i = 1
Poderes de los n??meros complejos
Potencias enteras de n??meros complejos se definen por la multiplicaci??n repetida o divisi??n que el anterior. Potencias complejas de reales positivos se definen a trav??s de correos x que el anterior. Estas son funciones continuas. Tratando de extender estas funciones para el caso general de poderes no entero de n??meros complejos que no son reales positivos conduce a dificultades. O nos definimos funciones discontinuas o funciones multiformes. Ninguna de estas opciones son del todo satisfactorios.
El poder racional de un n??mero complejo debe ser la soluci??n de una ecuaci??n algebraica. Por ejemplo, w = z media debe ser una soluci??n a la ecuaci??n w = 2 z. Pero si w es una soluci??n, entonces tambi??n lo es - w, porque (-1) 2 = 1. As?? que la ecuaci??n algebraica w 2 = z no es suficiente para definir z media. La elecci??n de una de las dos soluciones como el valor principal de z medio nos deja con una funci??n que no es continua, y las normas habituales para la manipulaci??n de poderes nos llevan por mal camino.
El logaritmo de un n??mero complejo
Una soluci??n, z = log a, a la ecuaci??n e z = a, se llama la valor principal del logaritmo complejo. Es la ??nica soluci??n imaginaria cuya parte se encuentra en el . intervalo (-π, π] Por ejemplo, log 1 = 0, log (-1) = π i, i = π sesi??n i / 2, y log (-. i) = i -π / 2 El valor principal de el logaritmo se conoce como una rama del logaritmo; otras ramas pueden ser especificados por la elecci??n de un rango diferente para la parte imaginaria del logaritmo El l??mite entre las ramas se conoce como a. rama cortada. El valor principal tiene una rama cortada que se extiende desde el origen a lo largo del eje real negativo, y es discontinua en cada punto de la rama cortada.
Potencia compleja de un n??mero complejo
El complejo de poder un general b de un n??mero complejo distinto de cero se define como una
Cuando el exponente es un n??mero racional z potencia = a n / m es una soluci??n de la ecuaci??n z = m a n.
El c??lculo de potencias complejas se facilita mediante la conversi??n de la base una a la forma polar, como se describe en detalle a continuaci??n .
Ra??ces complejas de la unidad
Un n??mero complejo a tal que a n = 1 para un n??mero entero positivo n es un n-??simo de la ra??z de la unidad. Geom??tricamente, la en??sima ra??ces de la unidad en el c??rculo unitario del plano complejo en los v??rtices de un n gon regular con un v??rtice en el verdadero n??mero 1.
Si z n = 1, pero z k ≠ 1 para todos los n??meros naturales k tal que 0 <k <n, entonces z se denomina n ?? ra??z primitiva de la unidad. La unidad negativo -1 es la ??nica ra??z cuadrada primitiva de la unidad. La unidad imaginaria i es uno de los dos primitivas 4-th ra??ces de la unidad; el otro es - i.
El n??mero e 2 πi (1 / n) es el n ?? ra??z primitiva de la unidad con el m??s peque??o positivo argumento complejo. (A veces se llama el director en??sima ra??z de la unidad, aunque esta terminolog??a no es universal y no se debe confundir con la valor principal de n √ 1, que es 1.)
Los otros n th ra??ces de la unidad est??n dadas por
para 2 ≤ k ≤ n.
Las ra??ces de n??meros complejos arbitrarios
Aunque hay un n??mero infinito de valores posibles para un logaritmo complejo en general, s??lo hay un n??mero finito de valores para la potencia de una z en el caso especial importancia cuando z = 1 / n y n es un entero positivo. Estos son el n-??simo ra??ces de una; son soluciones de la ecuaci??n x n = a. Al igual que con ra??ces reales, una segunda ra??z tambi??n se llama una ra??z cuadrada y una tercera ra??z tambi??n se llama una ra??z c??bica.
Es convencional en matem??ticas para definir un 1 / n como el valor principal de la ra??z. Si a es un n??mero real positivo, tambi??n es convencional para seleccionar un n??mero real positivo como el valor principal de la ra??z de un 1 / n. Para los n??meros complejos generales, la n-??sima ra??z con el argumento m??s peque??o a menudo se selecciona como el valor principal de la n-??sima operaci??n de ra??z, al igual que con los valores principales de ra??ces de la unidad.
El conjunto de n-??simo ra??ces de un n??mero complejo a se obtiene multiplicando el valor principal de un 1 / n por cada uno de los n-??simo ra??ces de la unidad. Por ejemplo, las ra??ces de la cuarta 16 son 2, -2, 2 i, i y -2, porque el valor principal de la ra??z cuarta de 16 es 2 y el cuarto ra??ces de la unidad son 1, -1, i, y - yo.
C??lculo de potencias complejas
A menudo es m??s f??cil de calcular potencias complejas escribiendo el n??mero que se va a exponentes en forma polar . Cada n??mero complejo z se puede escribir en la forma polar
donde r es un n??mero real no negativo y θ es el (real) argumento de z. El argumento, como el logaritmo complejo, tiene muchos valores posibles para cada z y as?? una rama cortada se utiliza para elegir un valor espec??fico. La forma polar tiene una interpretaci??n geom??trica simple: si un n??mero complejo u + iv se considera como la representaci??n de un punto (u, v) en el plano complejo usando coordenadas cartesianas , entonces (r, θ) es el mismo punto en coordenadas polares . Es decir, r es el "radio" r 2 = u 2 + v 2 y θ es el "??ngulo" θ = atan2 (v, u). El corte rama corresponde a la idea de que un ??ngulo polar θ es ambigua, ya que se podr??a a??adir cualquier m??ltiplo de 2π a θ sin cambiar la ubicaci??n del punto. El valor principal (la rama cortada m??s com??n), como se mencion?? anteriormente, corresponde a θ elegido en el intervalo (-π, π].
Con el fin de calcular la potencia compleja a b, escribir una en forma polar:
 .
.
Entonces
y por lo tanto
Si b se descompone como c + di, a continuaci??n, la f??rmula para una b se puede escribir de forma m??s expl??cita como
Esta f??rmula final permite potencias complejas para ser calculadas f??cilmente de descomposiciones de la base en forma polar y el exponente en forma cartesiana. Se muestra aqu?? tanto en forma polar y en forma cartesiana (a trav??s de la identidad de Euler).
Los siguientes ejemplos utilizan el valor principal, la rama cortada que causa θ estar en el intervalo (-π, π] Para calcular i i, i escribir en formas polares y cartesianas.:
Entonces la f??rmula anterior, con r = 1, θ = π / 2, c = 0, y d = 1, se obtiene:
Del mismo modo, para encontrar (-2) 3 + 4 i, calcular la forma polar de -2,
y utilizar la f??rmula anterior para calcular
El valor de una potencia compleja depende de la rama utilizado. Por ejemplo, si la forma polar i = 1 e i (5π / 2) se utiliza para calcular i i, la alimentaci??n se encontr?? que e -5π / 2; el valor principal de i i, calculado anteriormente, es e -π / 2.
El fracaso de las identidades de potencia y logaritmo
Identidades para potencias y logaritmos que tienen para los n??meros reales positivos pueden fallar cuando los n??meros reales positivos son reemplazados por n??meros complejos arbitrarios. No hay un m??todo para definir poderes complejos o el complejo logaritmo como funciones de valores complejos preservando al mismo tiempo las identidades estas operaciones poseen en los n??meros reales positivos.
Un ejemplo que implica logaritmos se refiere a la regla log (a b) = b ?? conectarse a, que tiene cada vez que a es un n??mero real positivo y b es un n??mero real. El siguiente c??lculo muestra que esta identidad no se sostiene, en general, para el valor principal del logaritmo complejo cuando una no es un n??mero real positivo:
Independientemente de que se utilice la rama del logaritmo, siempre existir?? un fallo similar de la identidad.
Un ejemplo que implica reglas de potencia se refiere a las identidades
Estas identidades son v??lidas cuando a y b son n??meros reales positivos y c es un n??mero real. Sin embargo, un c??lculo utilizando los valores principales muestra que
y
Estos ejemplos ilustran que los poderes complejos y logaritmos no se comportan de la misma manera que sus hom??logos reales, por lo que se requiere precauci??n al trabajar con las complejas versiones de estas operaciones.
Zero a la potencia cero
La evaluaci??n de 0 0 presenta un problema, porque diferente razonamiento matem??tico conduce a resultados diferentes. La mejor opci??n para su valor depende del contexto. Seg??n Benson (1999), "La opci??n si desea definir 0 0 se basa en la conveniencia, no en la correcci??n." Existen dos tratamientos principales en la pr??ctica, una de las matem??ticas discretas y el otro de an??lisis.
En muchos lugares, especialmente en las fundaciones y la combinatoria, 0 0 se define como 1. Esta definici??n surge en tratamientos fundamentales de los n??meros naturales como cardenales finitos , y es ??til para acortar las identidades combinatorias y eliminar los casos especiales de teoremas, como se ilustra a continuaci??n. En muchos otros entornos, 0 0 queda sin definir. En el c??lculo , 0 0 es un forma indeterminada, que debe ser analizado en lugar de evaluar. En general, el an??lisis matem??tico trata 0 0 como indefinido a fin de que la funci??n exponencial ser continua.
Justificaciones para definir 0 0 = 1 incluyen:
- Cuando 0 0 se considerar?? como un vac??o producto de ceros, su valor es 1.
- La interpretaci??n combinatoria de 0 0 es el n??mero de tuplas vac??as de elementos del conjunto vac??o. No es exactamente un vac??o tupla.
- De manera equivalente, la interpretaci??n de teor??a de conjuntos de 0 0 es el n??mero de funciones del conjunto vac??o al conjunto vac??o. Hay exactamente un tal funci??n, el funci??n vac??a.
- Simplifica enormemente la teor??a de polinomios y series de potencias que un t??rmino constante puede hacha 0 escrito para una x arbitrario. Por ejemplo:
- La f??rmula para los coeficientes en un producto de polinomios perder??a gran parte de su simplicidad si t??rminos constantes tuvieron que ser tratados de manera especial.
- Una serie de potencias como
 no es v??lida para x = 0 a menos que 0 0, que aparece en el numerador del primer t??rmino de la serie, es 1. De lo contrario habr??a que usar la identidad ya
no es v??lida para x = 0 a menos que 0 0, que aparece en el numerador del primer t??rmino de la serie, es 1. De lo contrario habr??a que usar la identidad ya 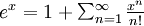 .
. - La teorema del binomio
 no es v??lido para x = 0, a menos que 0 0 = 1. Al definir 0 0 ser 1, un caso especial del teorema puede ser eliminada.
no es v??lido para x = 0, a menos que 0 0 = 1. Al definir 0 0 ser 1, un caso especial del teorema puede ser eliminada.
- En c??lculo diferencial, el regla de la potencia
 no es v??lida para n = 1 en x = 0 a menos que 0 0 = 1. La definici??n de esta manera elimina la necesidad de un caso especial de la regla de la potencia.
no es v??lida para n = 1 en x = 0 a menos que 0 0 = 1. La definici??n de esta manera elimina la necesidad de un caso especial de la regla de la potencia.
En contextos donde el exponente puede variar de forma continua, por lo general es mejor para tratar 0 0 como una cantidad definida. Las justificaciones para tratarla como indefinido incluyen:
- El valor 0 0 surge a menudo como el l??mite formal de funciones exponenciadas, f (x) g (x), cuando f (x) yg (x) Enfoque 0 cuando x tiende a un (una constante o infinito). All??, 0 0, sugiere [lim f (x)] lim g (x), que es una cantidad bien definida y es el valor correcto de lim f (x) g (x), cuando no nulos constantes f y g de aproximaci??n, pero no es bien definido cuando enfoque fyg 0. El mismo razonamiento se aplica a ciertos poderes que implican el infinito ,
 y
y  . Una forma m??s abstracta de decir esto es la siguiente: La funci??n real x y de las dos variables reales no negativos x e y no es continua en el punto (x, y) = (0, 0), y as?? 0 0 no est?? determinado por la continuidad. Es decir, la funci??n de x y no tiene extensi??n continua desde el primer cuadrante abierto para incluir el punto (0,0). La regla de c??lculo, que
. Una forma m??s abstracta de decir esto es la siguiente: La funci??n real x y de las dos variables reales no negativos x e y no es continua en el punto (x, y) = (0, 0), y as?? 0 0 no est?? determinado por la continuidad. Es decir, la funci??n de x y no tiene extensi??n continua desde el primer cuadrante abierto para incluir el punto (0,0). La regla de c??lculo, que 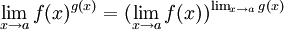 cada vez que se definen los dos lados de la ecuaci??n, ser??a un error si se definieron 0 0.
cada vez que se definen los dos lados de la ecuaci??n, ser??a un error si se definieron 0 0. - La funci??n de z z, visto como una funci??n de un n??mero complejo z variable y definido como log e z z no est?? definida para z = 0 porque log z est?? definido en z = 0. Adem??s, debido a z z tiene un logar??tmica punto de ramificaci??n en z = 0, no es com??n para extender el dominio de z z al origen en este contexto.
Tratamiento en lenguajes de programaci??n
Los lenguajes de programaci??n que eval??an 0 0 sean 1 incluyen J, Java , Python , Ruby, Haskell, ML, Esquema, MATLAB y Calculadora de Microsoft Windows ".
Arce simplifica un 0 a 1 y 0 a un 0, incluso si no hay limitaciones se colocan en una, y eval??a 0 0 a 1.
Google b??squeda cuando utiliza por su funci??n de calculadora eval??a 0 0 a 1.
Mathematica simplifica un 0 a 1, incluso si no hay limitaciones se colocan en una. No simplificar 0 a, y se tarda 0 0 a haber una forma indeterminada.
En el .NET Framework, el m??todo System.Math.Pow trata a 0 0 que es 1.
Potencias con el infinito
Expresiones exponenciales que implican el infinito pueden ser considerados como generalizaciones de tipos m??s familiares de exponenciaci??n, pero hay por lo menos dos tipos claramente distintas de generalizaci??n al caso infinito. Por un lado, existe la combinatoria interpretaci??n te??rica o conjunto; ver exponenciaci??n de n??meros cardinales .
Por otra parte, uno puede encontrar expresiones tales como  y
y  Con origen en el an??lisis de la misma raz??n que 0 0, y ellos no est??n definidos por la misma raz??n. Es decir, es cierto que (lim f (x)) lim g (x) = lim f (x) g (x) cuando constantes distinto de cero finitos f y g de aproximaci??n, pero no cuando se acercan a 0 o infinito; entonces, el l??mite de la potencia puede ser cualquier cosa, no predecible a partir de los l??mites de f y g.
Con origen en el an??lisis de la misma raz??n que 0 0, y ellos no est??n definidos por la misma raz??n. Es decir, es cierto que (lim f (x)) lim g (x) = lim f (x) g (x) cuando constantes distinto de cero finitos f y g de aproximaci??n, pero no cuando se acercan a 0 o infinito; entonces, el l??mite de la potencia puede ser cualquier cosa, no predecible a partir de los l??mites de f y g.
Tiene sentido decir que 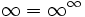 si esto es simplemente interpretarse como una abreviatura para el teorema de que si fyg tanto enfoque infinito cuando x tiende a, entonces lim f (x) g (x) es tambi??n infinita. (Del mismo modo,
si esto es simplemente interpretarse como una abreviatura para el teorema de que si fyg tanto enfoque infinito cuando x tiende a, entonces lim f (x) g (x) es tambi??n infinita. (Del mismo modo,  ,
,  , Etc.)
, Etc.)
De manera eficiente el c??lculo de un poder
El m??todo m??s simple de calcular un n requiere operaciones de multiplicaci??n n -1, pero se puede calcular de manera m??s eficiente, como se ilustra mediante el siguiente ejemplo. Para calcular 2 100, tenga en cuenta que el 100 = 96 + 4 y 96 = 3 * 32. Calcule el siguiente orden:
- 2 2 = 4
- (2 2) 2 = 2 4 = 16
- (2 4) 2 = 2 8 = 256
- (2 8) 2 = 2 16 = 65.536
- (2 16) 2 = 2 32 = 4294967296
- 2 32 2 32 2 32 2 4 = 2 100
Esta serie de pasos s??lo requiere 8 operaciones de multiplicaci??n en lugar de 99.
En general, el n??mero de operaciones de multiplicaci??n necesarios para calcular un n puede ser reducido a Θ (log n) mediante el uso de exponenciaci??n elevando al cuadrado o (en general) exponenciaci??n Adem??s de cadena. Encontrar la secuencia m??nima de multiplicaciones (la cadena Adem??s de longitud m??nima para el exponente) para un n es un problema dif??cil para los que se conocen actualmente no hay algoritmos eficientes, pero muchos algoritmos heur??sticos razonablemente eficientes est??n disponibles.
Notaci??n exponencial para los nombres de funciones
Depositar un exponente entero despu??s del nombre o s??mbolo de una funci??n, como si la funci??n estuviera siendo elevado a una potencia, com??nmente se refiere a repetirse la composici??n de funciones en lugar de multiplicaci??n repetida. Por lo tanto f 3 (x) puede significar f (f (f (x))); En particular, f -1 (x) generalmente denota la funci??n inversa de f.
Sin embargo, por razones hist??ricas, una sintaxis especial se aplica a las funciones trigonom??tricas : un exponente positivo aplicado a la abreviatura de la funci??n significa que el resultado se eleva a ese poder, mientras que un exponente de -1 indica la funci??n inversa. Es decir, el pecado 2 x es s??lo una forma abreviada de escribir (sen x) 2 sin utilizar par??ntesis, mientras que sin -1 x se refiere a la funci??n inversa de la sinusoidal, tambi??n llamado arcsin x. No hay necesidad de una forma abreviada de los inversos de las funciones trigonom??tricas, ya que cada una tiene su propio nombre y abreviatura, por ejemplo 1 / sin (x) = (sen x) -1 es csc x. Una convenci??n similar se aplica a logaritmos, donde log 2 (x) = (log (x)) 2 y no hay abreviatura com??n para log (log (x)).
Las generalizaciones de exponenciaci??n
Exponenciaci??n en ??lgebra abstracta
Exponenciación para exponentes enteros se puede definir para estructuras muy generales enálgebra abstracta.
Deje X ser un conjunto con un poder asociativo operación binaria, lo que vamos a escribir multiplicativamente. En esta situación muy general, podemos definir x n para cualquier elemento x de X y cualquier nulo número natural n , simplemente multiplicando x por sí mismo n veces; por definición, la asociatividad de energía significa que no importa en qué orden realizamos las multiplicaciones.
Ahora, además, suponer que la operación tiene un elemento de identidad 1. Entonces podemos definir x 0 sea igual a 1 para cualquier x . Ahora x n está definida para cualquier número natural n , incluyendo 0.
Finalmente, supongamos que la operación tiene inversos, y que la multiplicación es asociativa (de modo que el magma es un grupo ). Entonces podemos definir x -n ser la inversa de x n cuando n es un número natural. Ahora x n se define para cualquier número entero n y cualquier x en el grupo.
Exponenciación en este sentido puramente algebraica satisface las siguientes leyes (siempre que se definen ambos lados):
Aquí, nosotros usamos una división barra ("/") para indicar multiplicando por un inverso, con el fin de reservar el símbolo x -1 para elevar x a la potencia -1, en ??????lugar de la inversa de x . Sin embargo, como una de las leyes anteriores estados, x -1 es siempre igual a la inversa de x , por lo que la notación no importa en el extremo.
Si, además, la operación de multiplicación esconmutativa(de modo que el conjuntoXes ungrupo abeliano), entonces tenemos algunas leyes adicionales:
- (xy)n=xnyn
- (x/y)n=xn/yn
Si tomamos toda esta teoría de la exponenciación en un contexto algebraico pero escribimos la operación binaria aditiva ", multiplicación exponenciación se repite", entonces puede ser reinterpretado como " multiplicación se repite además ". Por lo tanto, cada una de las leyes de la exponenciación anterior tiene un análogo de entre leyes de la multiplicación.
Cuando uno tiene varias operaciones en todo, cualquiera de los cuales podría repetirse usando exponenciación, es común para indicar qué operación se repite colocando su símbolo en el exponente. Por lo tanto, x *n es x * ··· * x , mientras que x #n es x # ··· # x , cualesquiera que sean las operaciones * y # sean.
Se utiliza la notación superíndice también, especialmente en la teoría de grupos , para indicar la conjugación. Es decir, g h = h -1 gh , donde g y h son elementos de algún grupo . Aunque Conjugación obedece algunas de las mismas leyes que la exponenciación, no es un ejemplo de multiplicación repetida en ningún sentido. La quandle es una estructura algebraica en la que estas leyes de la conjugación juegan un papel central.
Exponenciación sobre conjuntos
Si n es un número natural y A es un conjunto arbitrario, la expresión A n menudo se utiliza para designar el conjunto de ordenadas n -tuplas de elementos de A . Esto es equivalente a dejar una n denotan el conjunto de funciones del conjunto {0, 1, 2, ..., n -1} al conjunto A ; el n tupla ( un 0 , una 1 , una 2 , ..., a n-1 ) representa la función que envía i una a yo .
Para un infinito número cardinal ?? y un conjunto A , la notación A ?? también se utiliza para designar el conjunto de todas las funciones de un conjunto de ?? tamaño a una . Esto se escribe a veces ?? A para distinguirlo de exponenciación cardinal, se define a continuación.
Este exponencial generalizada también se puede definir para las operaciones en conjuntos o para conjuntos con supletoria estructura. Por ejemplo, en el álgebra lineal , que tiene sentido índice sumas directas de espacios vectoriales sobre conjuntos de índices arbitrarios. Es decir, podemos hablar de
donde cada V yo es un espacio vectorial. Entonces si V yo = V para cada i , la suma directa resultante puede escribirse en notación exponencial como V (+)N , o simplemente V N con el entendimiento de que la suma directa es la opción predeterminada. Podemos nuevo reemplace el conjunto N con un número cardinal n para obtener V n , aunque sin elegir un estándar específico establecido con cardinalidad n , esto sólo se define hasta el isomorfismo. Tomando V para ser el campo R de los números reales (pensado como un espacio vectorial sobre sí mismo) y n que haber algún número natural , obtenemos el espacio vectorial que se estudia con mayor frecuencia en el álgebra lineal, el espacio euclidiano R n .
Si la base de la operación de exponenciación es un conjunto, la operación de exponenciación es el producto cartesiano menos que se indique lo contrario. Desde múltiples productos cartesianos producen un n - tupla, que puede representarse por una función en un conjunto de cardinalidad apropiada, S N se convierte en simplemente el conjunto de todas las funciones de N a S en este caso:
Esto concuerda con la potenciación de los números cardinales, en el sentido que | S N | = | S | |N| , donde | X | es la cardinalidad de X . Cuando N = 2 = {0,1}, tenemos | 2 X | = 2 |X| , donde 2 X , por lo general denota por P X , es el conjunto potencia de X ; cada subconjunto Y de X corresponde únicamente a una función de X toma el valor 1 para x ??? Y y 0 para x ??? Y .
Exponenciación en teoría de la categoría
En un Cartesiana categoría cerrada, la operación exponencial se puede utilizar para levantar un objeto arbitrario del poder de otro objeto. Esto generaliza el producto cartesiano en la categoría de conjuntos.
Exponenciación de números cardinales y ordinales
Enla teoría de conjuntos, hay operaciones exponenciales paracardinalyordinalnúmeros.
Si ?? y ?? son números cardinales, la ?? expresión ?? representa la cardinalidad del conjunto de las funciones de cualquier conjunto de cardinalidad ?? a cualquier conjunto de cardinalidad ??. Si ?? y ?? son finitos, entonces esto está de acuerdo con la operación exponencial ordinaria. Por ejemplo, el conjunto de 3-tuplas de elementos de un conjunto de 2 elementos tiene cardinalidad 8.
Exponenciación de números cardinales es distinta de la exponenciación de números ordinales , que está definido por un límite de proceso. En los números ordinales, exponenciación se define por inducción transfinito. Para ordinales ?? y ??, la ?? exponencial ?? es el supremo del producto ordinal alpha ?? alpha sobre toda ?? <??.
Exponenciación repetida
Así como la exponenciación de números naturales está motivada por la multiplicación repetida, es posible definir una operación basada en la exponenciación repetido; esta operación se denomina a veces tetración. Iterando tetración conduce a otra operación, y así sucesivamente. Esta secuencia de operaciones es capturada por la función de Ackermann.
Exponenciación en lenguajes de programación
La notación superíndice x y es conveniente en la escritura, pero inconveniente para máquinas de escribir y terminales de ordenador que se alinean las líneas de base de todos los caracteres de cada línea. Muchos lenguajes de programación tienen formas alternativas de expresar exponenciación que no usan superíndices:
- x ??? y:Algol,Commodore BASIC
- x ^ y:BASIC, J, Matlab, R, Microsoft Excel,TeX(y sus derivados),Haskell (para exponentes enteros), y la mayoría delos sistemas de álgebra computacional
- x ** y: Ada, Bash, Fortran, FoxPro,Perl,Python, Ruby, SAS,ABAP, Haskell (por exponentes de coma flotante), Turing
- x * y: APL
- Potencia (x, y): Microsoft Excel, Delphi / Pascal (declarada en "Math" -Unidad)
- pow (x, y):C,C ++, PHP
- Math.pow (x, y):Java, JavaScript Modula-3
- Math.pow (x, y): C #
- (Xy expt):Common Lisp, Esquema
En Bash, C, C ++, C #, Java, JavaScript, PHP y Python, el símbolo ^ representa bit a bit XOR. En Pascal, representa indirección.
Historia de la notación
El término de energía fue utilizado por Euclides para el cuadrado de una línea. Nicolas Chuquet utiliza una forma de notación exponencial en el siglo 15, que más tarde fue utilizado por Henricus grammateus y Michael Stifel. Samuel Jeake introducido el término índices en 1696. En el siglo 16 Robert Recorde utiliza los términos cuadrado, cubo, zenzizenzic (cuarto poder), surfolide (quinto), zenzicube (sexto), segundo surfolide (séptimo) y Zenzizenzizenzic (octavo).
Otro sinónimo histórico,la involución, es poco frecuente y no debe confundirse consu significado más común.





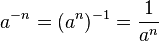
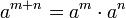

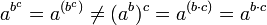
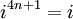

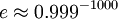





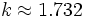
![5 ^ k \ aprox 5 ^ {1,732} = 5 ^ {433/250} = \ sqrt [250] {5 ^ {433}} \ aprox 16.241.](../../images/115/11503.png)




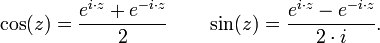

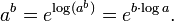




![\ Left (r ^ ce ^ {- d \ theta} \ right) e ^ {i (d \ log r + c \ theta)} = \ left (r ^ ce ^ {- d \ theta} \ right) \ left [\ cos (d \ log r + c \ theta) + i \ sin (d \ log r + c \ theta) \ right].](../../images/115/11517.png)