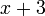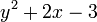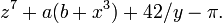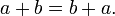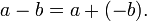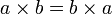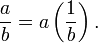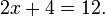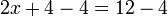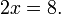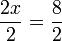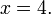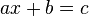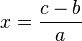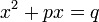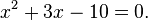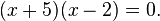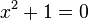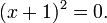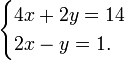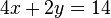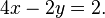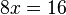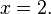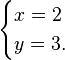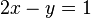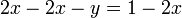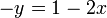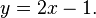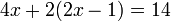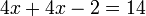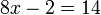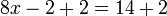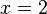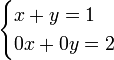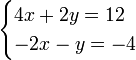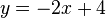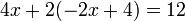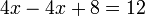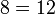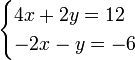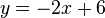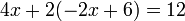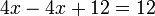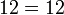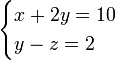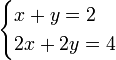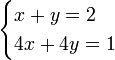Álgebra elemental
Antecedentes de las escuelas de Wikipedia
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. Una rápida conexión para el apadrinamiento de niños es http://www.sponsor-a-child.org.uk/
Álgebra elemental es una forma fundamental y relativamente básico de álgebra enseñados a los estudiantes que se presume que tienen poco o ningún conocimiento formal de las matemáticas más allá de la aritmética . Mientras que en la aritmética sólo números y sus operaciones aritméticas (como +, -, ×, ÷) se producen, en álgebra también se utiliza símbolos (como X e Y, o A y B) para denotar números. Estos se llaman variables. Esto es útil porque:
- Permite que la generalización de la aritmética ecuaciones (y desigualdades ) para ser declarados como leyes (como
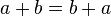 para todos ayb), y por lo tanto es el primer paso para el estudio sistemático de las propiedades del sistema de números reales .
para todos ayb), y por lo tanto es el primer paso para el estudio sistemático de las propiedades del sistema de números reales . - Permite referencia a los números que no son conocidos. En el contexto de un problema, una variable puede representar un cierto valor de las cuales es incierto, pero puede ser resuelto mediante la formulación y manipulación de ecuaciones.
- Permite la exploración de las relaciones matemáticas entre cantidades (como "si usted vende x entradas, entonces su ganancia será
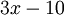 dólares ").
dólares ").
Estos tres son los principales capítulos de álgebra elemental, que deben distinguirse de álgebra abstracta , un tema más avanzado generalmente enseñó a los estudiantes universitarios.
En álgebra elemental, un " . la expresión "puede contener números, variables y operaciones aritméticas Estos se suelen escribir (por convenio) con términos 'de mayor potencia" a la izquierda (ver polinomio ); algunos ejemplos son:
En álgebra más avanzada, una expresión puede incluir también funciones elementales.
Una " ecuación "es la afirmación de que dos expresiones son iguales. Algunas ecuaciones son verdaderas para todos los valores de las variables involucradas (como 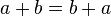 ); tales ecuaciones se denominan " "." identidades ecuaciones condicionales "son verdaderas sólo para algunos valores de las variables involucradas:
); tales ecuaciones se denominan " "." identidades ecuaciones condicionales "son verdaderas sólo para algunos valores de las variables involucradas: 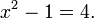 Los valores de las variables que conforman la ecuación verdadera se llaman las "soluciones" de la ecuación.
Los valores de las variables que conforman la ecuación verdadera se llaman las "soluciones" de la ecuación.
Leyes del álgebra elemental
- Conmutativa propiedad de adición
- La resta es la inversa de la adición.
- Para restar es el mismo que para agregar un número negativo :
- Ejemplo: si
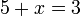 entonces
entonces 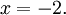
- Propiedad conmutativa de la multiplicación
- División es el inverso de la multiplicación.
- Para dividir es el mismo que multiplicar por una recíproco:
- Exponenciación no es una operación conmutativa.
- Por lo tanto exponenciación tiene un par de operaciones inversas: logaritmo y exponenciación con exponentes fraccionarios (por ejemplo, raíces cuadradas ).
- Ejemplos: si
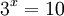 entonces
entonces 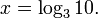 Si
Si 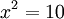 entonces
entonces 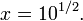
- Ejemplos: si
- Las raíces cuadradas de números negativos no existen en el sistema de números reales. (Véase: sistema de números complejos )
- Por lo tanto exponenciación tiene un par de operaciones inversas: logaritmo y exponenciación con exponentes fraccionarios (por ejemplo, raíces cuadradas ).
- Asociativa propiedad de adición:
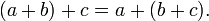
- Propiedad asociativa de la multiplicación:
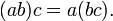
- Propiedad distributiva de la multiplicación con respecto a la adición:
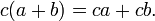
- Propiedad distributiva de la exponenciación con respecto a la multiplicación:

- ¿Cómo combinar los exponentes:
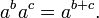
- Poder a una propiedad potencias de los exponentes:
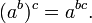
La ley de igualdad
- Si
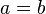 y
y 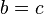 , A continuación,
, A continuación,  ( transitividad de igualdad).
( transitividad de igualdad).  ( reflexividad de la igualdad).
( reflexividad de la igualdad). - Si
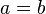 entonces
entonces 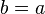 ( simetría de la igualdad).
( simetría de la igualdad).
Otras leyes
- Si
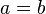 y
y 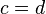 entonces
entonces 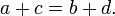
- Si
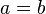 entonces
entonces 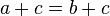 para cualquier c (propiedad además de la igualdad).
para cualquier c (propiedad además de la igualdad).
- Si
- Si
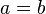 y
y 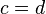 entonces
entonces 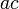 =
= 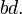
- Si
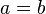 entonces
entonces 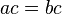 para cualquier c (propiedad de la multiplicación de la igualdad).
para cualquier c (propiedad de la multiplicación de la igualdad).
- Si
- Si dos símbolos son iguales, entonces uno puede ser sustituido por el otro a voluntad (principio de sustitución).
- Si
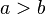 y
y 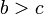 entonces
entonces 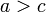 (Transitividad de desigualdad).
(Transitividad de desigualdad). - Si
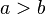 entonces
entonces 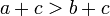 para cualquier c.
para cualquier c. - Si
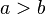 y
y 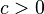 entonces
entonces 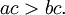
- Si
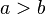 y
y 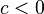 entonces
entonces 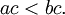
Ejemplos
Ecuaciones lineales en una variable
Las ecuaciones más simples de resolver son ecuaciones lineales que tienen una sola variable. Contienen sólo números constantes y una sola variable sin un exponente. Por ejemplo:
La técnica central es sumar, restar, multiplicar o dividir ambos lados de la ecuación por el mismo número con el fin de aislar la variable en un lado de la ecuación. Una vez que se aísla la variable, el otro lado de la ecuación es el valor de la variable. Por ejemplo, restando 4 de ambos lados de la ecuación anterior:
lo que simplifica a:
Dividiendo ambos lados por 2:
simplifica a la solución:
El caso general,
sigue el mismo formato para la solución:
Ecuaciones cuadráticas
Las ecuaciones cuadráticas pueden expresarse en la forma ax 2 + bx + c = 0, donde a no es cero (si fuera cero, entonces la ecuación cuadrática no sería pero lineal ). Debido a esto una ecuación cuadrática debe contener el término ax 2, que se conoce como el término cuadrático. De ahí a ≠ 0, y así podemos dividir por una y reorganizar la ecuación en la forma estándar
donde p = b / a y q = - c / a. La solución de este, mediante un proceso conocido como completar el cuadrado, conduce a la fórmula cuadrática .
Ecuaciones cuadráticas también pueden resolverse usando factorización (el proceso inverso de lo que es expansión, pero para dos términos lineales a veces se denominan foiling). Como ejemplo de factoring:
Lo cual es lo mismo que
Se desprende de lo propiedad del producto cero que, o bien x = 2 o x = -5 son las soluciones, ya que precisamente uno de los factores debe ser igual a cero . Todas las ecuaciones de segundo grado tendrán dos soluciones en el número complejo sistema, pero no necesitan tener ninguna en el número real del sistema. Por ejemplo,
no tiene solución número real ya que ningún número real al cuadrado es igual a -1. A veces una ecuación cuadrática tiene una raíz de multiplicidad 2, tales como:
Para esta ecuación, -1 es una raíz de multiplicidad 2.
Sistema de ecuaciones lineales
En el caso de un sistema de ecuaciones lineales , como, por ejemplo, dos ecuaciones con dos variables, a menudo es posible encontrar las soluciones de ambas variables que satisfacen ambas ecuaciones.
Primer método de encontrar una solución
Un ejemplo de un sistema de ecuaciones lineales podría ser la siguiente:
Multiplicando los términos de la segunda ecuación por 2:
Sumando las dos ecuaciones juntos para conseguir:
lo que simplifica a
Dado el hecho de que x = 2 se sabe, es entonces posible deducir que y = 3 por cualquiera de las dos ecuaciones originales (mediante el uso de 2 en lugar de x) La solución completa a este problema es entonces
Tenga en cuenta que esta no es la única manera de resolver este sistema específico; y se podría haber resuelto antes de x.
Segundo método para encontrar una solución
Otra forma de resolver el mismo sistema de ecuaciones lineales es por sustitución.
Un equivalente para y se puede deducir mediante el uso de una de las dos ecuaciones. Uso de la segunda ecuación:
Restando 2x de cada lado de la ecuación:
y multiplicando por -1:
El uso de este valor de y en la primera ecuación en el sistema original:
Adición de 2 a cada lado de la ecuación:
lo que simplifica a
Usando este valor en una de las ecuaciones, se obtiene la misma solución que en el método anterior.
Tenga en cuenta que esta no es la única manera de resolver este sistema específico; en este caso también, y se podría haber resuelto antes de x.
Otros tipos de sistemas de ecuaciones lineales
Sistemas irresolubles
En el ejemplo anterior, es posible encontrar una solución. Sin embargo, también hay sistemas de ecuaciones que no tienen una solución. Un ejemplo obvio sería:
La segunda ecuación en el sistema no tiene solución posible. Por lo tanto, este sistema no puede ser resuelto. Sin embargo, no todos los sistemas incompatibles se reconocen a primera vista. Como ejemplo, el siguiente sistema se estudia:
Al tratar de resolver este (por ejemplo, mediante el método de sustitución supra), la segunda ecuación, después de añadir - 2 x en ambos lados y multiplicando por -1, resultados en:
Y el uso de este valor para y en la primera ecuación:
No hay variables se fueron, y la igualdad no es cierto. Esto significa que la primera ecuación no puede proporcionar una solución para el valor para y obtenido en la segunda ecuación.
Sistemas indeterminados
También hay sistemas que tienen soluciones múltiples o infinitas, en oposición a un sistema con una solución única (es decir, dos valores únicos para x e y) Por ejemplo:
El aislamiento y en la segunda ecuación:
Y el uso de este valor en la primera ecuación del sistema:
La igualdad es cierto, pero no proporciona un valor para x. De hecho, se puede verificar fácilmente (con sólo rellenar en algunos valores de x) que para cualquier x hay una solución, siempre y cuando y = -2 x + 6. Hay infinitas soluciones para este sistema.
Una y sistemas indeterminados
Los sistemas con más variables que el número de ecuaciones lineales no tienen una solución única. Un ejemplo de tal sistema es
Tal sistema se llama indeterminado; cuando se trata de encontrar una solución, una o más variables sólo se pueden expresar en relación con las otras variables, pero no se pueden determinar numéricamente. Incidentalmente, un sistema con un mayor número de ecuaciones que variables, en los que necesariamente algunas ecuaciones son sumas o múltiplos de otros, se llama sobredeterminado.
Relación entre Solvencia y Multiplicidad
Dado cualquier sistema de ecuaciones lineales, hay una relación entre la multiplicidad y la solvencia.
Si una ecuación es una múltiplo de la otra (o, más generalmente, una suma de múltiplos de las otras ecuaciones), entonces el sistema de ecuaciones lineales es indeterminado, lo que significa que el sistema tiene infinitas soluciones. Ejemplo:
Cuando la multiplicidad es sólo parcial (lo que significa que por ejemplo, sólo los lados de la mano izquierda de las ecuaciones son múltiplos, mientras que los lados mano derecha no son o no por el mismo número) entonces el sistema es insoluble. Por ejemplo, en
los segundos rendimientos ecuación que x + y = 1/4, que está en contradicción con la primera ecuación. Este sistema también se llama inconsistente en el idioma del álgebra lineal . Al tratar de resolver un sistema de ecuaciones lineales es generalmente una buena idea para comprobar si una ecuación es un múltiplo de la otra. Si esto es precisamente lo tanto, la solución no se puede determinar de forma exclusiva. Si esto es sólo parcialmente, no existe la solución.
Esto, sin embargo, no significa que las ecuaciones deben ser múltiplos de sí para tener una solución, como se muestra en los apartados anteriores; En otras palabras: la multiplicidad en un sistema de ecuaciones lineales no es una condición necesaria para la solvencia.