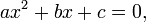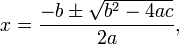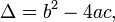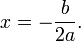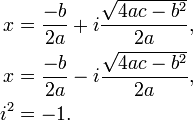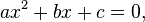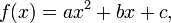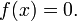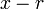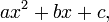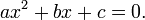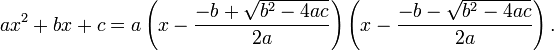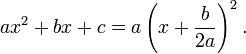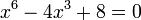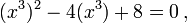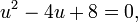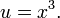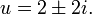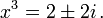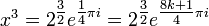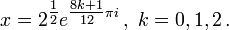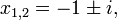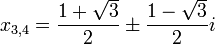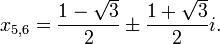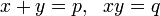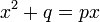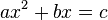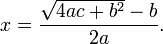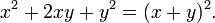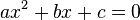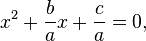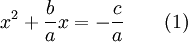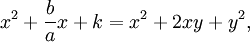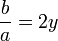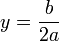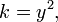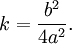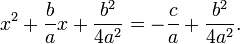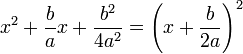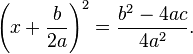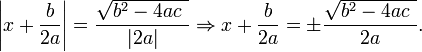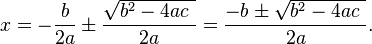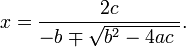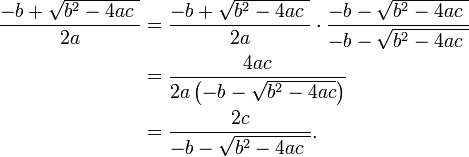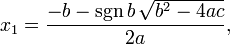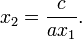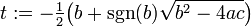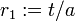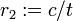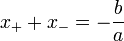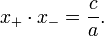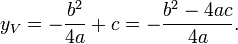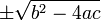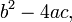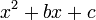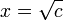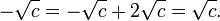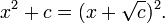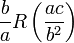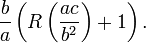Ecuación cuadrática

Temas relacionados: Matemáticas

Antecedentes

SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...

En matemáticas , una ecuación de segundo grado es un polinomio de la ecuación de la segunda grado. La forma general es

$ax ^ 2 + bx + c = 0, \, \!$

donde a ≠ 0. (Para a = 0, la ecuación se convierte en una ecuación lineal .)

Las letras a, b, y c son llamados coeficientes: el coeficiente cuadrático A es el coeficiente de 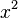$x ^ 2$ , El coeficiente lineal de b es el coeficiente de x, y c es la coeficiente constante, también llamado el término libre o término constante.

Ecuaciones cuadráticas se llaman cuadrática porque cuadrado es latina para "cuadrado"; en el término principal de la variable es al cuadrado.

Parcelas de bienes -valued función cuadrática ax ² + bx + c, variando cada coeficiente por separado

Fórmula cuadrática

Una ecuación cuadrática con reales o complejos coeficientes tiene dos soluciones (no necesariamente distintos), llamados raíces, que pueden ser reales o complejas, dadas por la fórmula cuadrática:

$x = \ frac {-b \ pm \ sqrt {b ^ 2-4ac}} {2a},$

donde el símbolo "±" indica que tanto

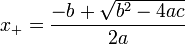
$x_ + = \ frac {-b + \ sqrt {b ^ 2-4ac}} {2a}$

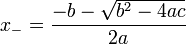
$\ X_- = \ frac {-b - \ sqrt {b ^ 2-4ac}} {2a}$

son soluciones.

En pocas palabras, ± 'más o menos' medios como posibilidades de ecuaciones.

Discriminante

Signos Ejemplo discriminantes
■ <0: x ² + _^1/2
■ = 0: - _^4/3 x ² + _^4/3 x - _^1/3
■> 0: _^3/2 x ² + _^1/2 x - _^4/3

En la fórmula anterior, la expresión bajo el signo de la raíz cuadrada:

$\ Delta = b ^ 2 - 4ac, \, \!$

se llama discriminante de la ecuación cuadrática.

Una ecuación de segundo grado con coeficientes reales puede tener una o dos raíces reales distintas, o dos raíces complejas distintas. En este caso el discriminante determina el número y la naturaleza de las raíces. Hay tres casos:

Si el discriminante es positivo, hay dos raíces distintas, ambos de los cuales son números reales. Para las ecuaciones de segundo grado con enteros coeficientes, si el discriminante es un cuadrado perfecto, entonces las raíces son números racionales -en otros casos pueden ser irracionales cuadráticos.
Si el discriminante es cero, no es exactamente una raíz distinta, y que la raíz es un número real . A veces llamado un raíz doble, su valor es:
$x = - \ frac {b} {2a}. \, \!$
Si el discriminante es negativo, no hay raíces reales. Más bien, hay dos distintos (no real) complejos raíces, que son complejos conjugados el uno del otro:
$\ Begin {align} x & = \ frac {-b} {2a} + i \ frac {\ sqrt {4ac - b ^ 2}} {2a}, \\ x & = \ frac {-b} {2a} - i \ frac {\ sqrt {4ac - b ^ 2}} {2a}, \\ i ^ 2 y = -1. \ End {align}$

Así, las raíces son distintas si y sólo si el discriminante es distinto de cero, y las raíces son reales si y sólo si el discriminante es no negativo.

Geometría

Para el función cuadrática:
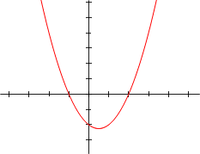
f (x) = x ² - x - 2 = (x + 1) (x - 2) de un verdadero variable x, la x - coordenadas de los puntos donde la gráfica cruza con el eje x, x = -1 y x = 2, son el raíces de la ecuación cuadrática: x ² - x - 2 = 0.

Las raíces de la ecuación cuadrática

$ax ^ 2 + bx + c = 0, \,$

son también el ceros de la función cuadrática:

$f (x) = ax ^ 2 + bx + c, \,$

ya que son los valores de x para los cuales

$f (x) = 0. \,$

Si a, b, y c son números reales , y la dominio de f es el conjunto de los números reales, entonces los ceros de f son exactamente x - coordenadas de los puntos donde la gráfica toca el eje x.

Se desprende de lo anterior que, si el discriminante es positivo, la gráfica toca el eje x en dos puntos, si es cero, los toques de gráfico en un punto, y si es negativa, la gráfica no toca el eje x.

Factorización cuadrática

El término

$x - r \,$

es un factor del polinomio

$ax ^ 2 + bx + c, \$

si y sólo si r es una raíz de la ecuación cuadrática

$ax ^ 2 + bx + c = 0. \$

Se deduce de la fórmula cuadrática que

$ax ^ 2 + bx + c = a \ left (x - \ frac {-b + \ sqrt {b ^ 2-4ac}} {2a} \ right) \ left (x - \ frac {-b - \ sqrt { b ^ 2-4ac}} {2a} \ right).$

En el caso especial en que el cuadrática tiene sólo una raíz distinta (es decir, el discriminante es cero), el polinomio cuadrático se puede factorizar como

$ax ^ 2 + bx + c = a \ left (x + \ frac {b} {2a} \ right) ^ 2. \, \!$

Aplicación a las ecuaciones de grado superior

Ciertas ecuaciones de grado superior se pueden poner en forma cuadrática y resueltos de esa manera. Por ejemplo, la ecuación de sexto grado en x:

$x ^ 6 - 4x ^ 3 + 8 = 0 \,$

puede reescribirse como:

$(X ^ 3) ^ 2 - 4 de (x ^ 3) + 8 = 0 \ ,,$

o, equivalentemente, como una ecuación cuadrática en una nueva variable u:

$u ^ 2 - 4u + 8 = 0, \,$

donde

$u = x ^ 3. \,$

La solución de la ecuación de segundo grado para obtener resultados U en las dos soluciones:

$u = 2 \ pm 2i.$

Así

$x ^ 3 = 2 \ pm 2i \ ,.$

La concentración en la búsqueda de las tres raíces cúbicas de

- Las otras tres soluciones para x será su conjugados complejos - reescritura del lado derecho usando La fórmula de Euler:

$x ^ 3 = 2 ^ {\ tfrac {3} {2}} e ^ {\ tfrac {1} {4} \ pi i} = 2 ^ {\ tfrac {3} {2}} e ^ {\ tfrac { 8k + 1} {4} \ pi i} \,$

(Ya que e ^{2 k π i} = 1), da las tres soluciones:

$x = 2 ^ {\ tfrac {1} {2}} e ^ {\ tfrac {8k + 1} {12} \ pi i} \ ,, ~ k = 0, 1, 2 \ ,.$

Usando la fórmula Eulers 'de nuevo junto con las identidades trigonométricas como cos (π / 12) =

, Y la adición de los conjugados complejos, da la colección completa de soluciones como:

$x_ {1,2} = -1 \ pm i, \,$

$x_ {3,4} = \ frac {1 + \ sqrt {3}} {2} \ pm \ frac {1 - \ sqrt {3}} {2} i \,$

$x_ {5,6} = \ frac. {1 - \ sqrt {3}} {2} \ pm \ frac {1 + \ sqrt {3}} {2} i \,$

Historia

Los babilonios, ya en 1800 aC (que se muestra en Antigua Babilonia tablillas de arcilla) podría resolver un par de ecuaciones simultáneas de la forma:

$x + y = p, \ \ xy = q \$

que son equivalentes a la ecuación:

$\ X ^ 2 + q = px$

La pareja original de ecuaciones se resuelve de la siguiente manera:

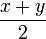
Forma $\ Frac {x + y} {2}$
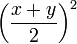
Forma $\ Left (\ frac {x + y} {2} \ right) ^ 2$
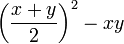
Forma $\ Left (\ frac {x + y} {2} \ right) ^ 2 - xy$
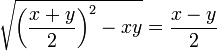
Forma $\ Sqrt {\ left (\ frac {x + y} {2} \ right) ^ 2 - xy} = \ frac {xy} {2}$
Encontrar $x, \ y$ mediante la inspección de los valores en (1) y (4).

En el Sulba Sutras en antiguo circa India 8vo siglo BCE ecuaciones de segundo grado de la forma ax ² = c y ax ² + bx = c se analizaron utilizando métodos geométricos. Matemáticos babilónicos desde alrededor del año 400 BCE y Matemáticos chinos desde circa 200 BCE utiliza el método de completar el cuadrado para resolver ecuaciones de segundo grado con raíces positivas, pero no tienen una fórmula general. Euclides , el matemático griego, elaboró un método geométrico más abstracto alrededor 300 antes de nuestra era.

En 628 CE, Brahmagupta dio la primera solución explícita (aunque todavía no completamente general) de la ecuación cuadrática:

$\ Ax ^ 2 + bx = c$

Para el número absoluto multiplicado por cuatro veces el [coeficiente de la] cuadrado, añadir el cuadrado de la [coeficiente del] medio plazo; la raíz cuadrada de la misma, menos el [coeficiente de la] término medio, que se divide por dos veces el [coeficiente de la] cuadrado es el valor. (Brahmasphutasiddhanta (traducción Colebrook, 1817, página 346)

Esto es equivalente a:

$x = \ frac {\ sqrt {4ac + b ^ 2} -b} {2a}.$

La Bakhshali manuscrito de fecha que se han escrito en la India en el siglo 7 EC contenía una fórmula algebraica para resolver ecuaciones de segundo grado, así como cuadrática ecuaciones indeterminadas (originalmente de tipo hacha / c = y). Mohammad bin Musa Al-kwarismi ( Persia , siglo noveno ) desarrollaron un conjunto de fórmulas que trabajaban para soluciones positivas. Su trabajo se basó en Brahmagupta. Abraham bar Hiyya Ha-Nasi (también conocido por el América nombre Savasorda) introdujo la solución completa a Europa en su libro Liber embadorum en el siglo 12 . Bhaskara II ( 1114- 1185), un indio matemático - astrónomo, dio la primera solución general de la ecuación de segundo grado con dos raíces.

La redacción del matemático chino Yang Hui ( 1238- 1298 dC) representa la primera en la que aparecen las ecuaciones cuadráticas con coeficientes negativos de 'x', aunque él lo atribuye a la anterior Liu Yi.

Derivación

La fórmula cuadrática se puede derivar por el método de completando el cuadrado, con el fin de hacer uso de la identidad algebraica:

$x ^ 2 + 2xy + y ^ 2 = (x + y) ^ 2. \, \!$

Dividiendo la ecuación de segundo grado

$ax ^ 2 + bx + c = 0 \, \!$

por una (que está permitido porque a es distinto de cero), se obtiene:

$x ^ 2 + \ frac {b} {a} x + \ frac {c} {a} = 0, \, \!$

$x ^ 2 + \ frac {b} {a} x = - \ frac {c} {a} \ qquad (1)$

La ecuación de segundo grado se encuentra ahora en una forma en la que el método de completar el cuadrado se puede aplicar. Para "completar el cuadrado" es encontrar alguna constante k tal que

$x ^ 2 + \ frac {b} {a} x + k = x ^ 2 + 2xy + y ^ 2, \, \!$

para otro y constante. Para que estas ecuaciones para ser verdad,

$\ Frac {b} {a} = 2y \!$

$y = \ frac {b} {2a} \, \!$

$k = y ^ 2, \, \!$

así

$k = \ frac {b ^ 2} {4a ^ 2}. \, \!$

La adición de este constante a la ecuación (1) produce

$x ^ 2 + \ frac {b} {a} x + \ frac {b ^ 2} {4a ^ 2} = - \ frac {c} {a} + \ frac {b ^ 2} {4a ^ 2} \. , \!$

El lado izquierdo es ahora una cuadrado perfecto porque

$x ^ 2 + \ frac {b} {a} x + \ frac {b ^ 2} {4a ^ 2} = \ left (x + \ frac {b} {2a} \ right) ^ 2$

El lado derecho se puede escribir como una sola fracción, con el denominador común de 4 a ^2. Esto da

$\ Left (x + \ frac {b} {2a} \ right) ^ 2 = \ frac {b ^ 2-4ac} {4a ^ 2}.$

Tomando la raíz cuadrada de ambos lados rendimientos

$\ Left | x + \ frac {b} {2a} \ right | = \ frac {\ sqrt {b ^ 2-4ac \}} {| 2a |} \ Rightarrow x + \ frac {b} {2a} = \ pm \ frac {\ sqrt {b ^ 2-4ac \}} {2a}.$

Aislar x, da

$x = - \ frac {b} {2a} \ pm \ frac {\ sqrt {b ^ 2-4ac \}} {2a} = \ frac {-b \ pm \ sqrt {b ^ 2-4ac \}} { 2a}.$

Fórmula alternativa

En algunas situaciones es preferible expresar las raíces en una forma alternativa.

$x = \ frac {2c} {- b \ mp \ sqrt {b ^ 2-4ac \}}.$

Esta alternativa requiere c ser distinto de cero; para, si c es cero, la fórmula da correctamente cero como una raíz, pero no da ninguna segunda raíz, que no sea cero. En lugar de ello, una de las dos opciones para ∓ produce una la división por cero, que es indefinido.

Las raíces son las mismas independientemente de la expresión que utilizamos; la forma alternativa es simplemente una variación algebraica de la forma común:

$\ Begin {align} \ frac {-b + \ sqrt {b ^ 2-4ac \}} {2a} y {} = \ frac {-b + \ sqrt {b ^ 2-4ac \}} {2a} \ cdot \ frac {-b - \ sqrt {b ^ 2-4ac \}} {- b - \ sqrt {b ^ 2-4ac \}} \\ & {} = \ frac {} {4ac 2a \ left (- b - \ sqrt {b ^ 2-4ac} \ right)} \\ & {} = \ frac {2c} {- b - \ sqrt {b ^ 2-4ac \}}. \ End {align}$

La fórmula alternativa puede reducir la pérdida de precisión en la evaluación numérica de las raíces, que pueden ser un problema si una de las raíces es mucho más pequeño que el otro en magnitud absoluta. El problema de la c posiblemente siendo cero se puede evitar mediante el uso de un enfoque mixto:

$x_1 = \ frac {-b - \ sgn b \, \ sqrt {b ^ 2-4ac}} {2a},$

$x_2 = \ frac {c} {ax_1}.$

Aquí sgn denota la firmar función.

Ejecución de punto flotante

Un cuidado punto de aplicación de ordenador flotante difiere un poco de ambas formas para producir un resultado robusto. Suponiendo que el discriminante, b ² -4 ac, es positivo y b es distinto de cero, el código será algo como lo siguiente.

$t: = - \ tfrac12 \ grande (b + \ sgn (b) \ sqrt {b ^ 2-4ac} \ grande) \, \!$

$r_ {1}: = t / a \, \!$

$r_ {2}: = c / t \, \!$

Aquí sgn (b) es el función de signo, donde sgn (b) es 1 si b es positivo y -1 si b es negativo; su uso se asegura de que las cantidades añadidas son del mismo signo, evitando cancelación catastrófico. El cálculo de r ₂ utiliza el hecho de que el producto de las raíces es c / a.

Fórmulas de Viète

Fórmulas de Viète dan una relación simple entre las raíces de un polinomio y sus coeficientes. En el caso del polinomio de segundo grado, toman la siguiente forma:

$x_ + + x_- = - \ frac {b} {a}$

$x_ + \ cdot x_- = \ frac {c} {a}.$

La primera fórmula anterior se obtiene una expresión conveniente cuando graficar una función cuadrática. Dado que la gráfica es simétrica con respecto a una línea vertical a través de la vértice, cuando hay dos raíces reales del vértice coordenada x se encuentra en la media de las raíces (o intersecciones). Por lo tanto la coordenada x del vértice está dada por la expresión:

$x_V = \ frac {x_ + + x_-} {2} = - \ frac {b} {2a}.$

La coordenada y se puede obtener sustituyendo el resultado anterior en la ecuación cuadrática dada, dando

$y_V = - \ frac {b ^ 2} {4a} + c = - \ frac {b ^ 2 - 4ac} {4a}.$

Las generalizaciones

La fórmula y su derivación permanecen correcta si los coeficientes a, b y c son números complejos , o más generalmente miembros de cualquier campo cuyo característica no es 2. (En un campo de la característica 2, el elemento 2 a es cero y es imposible dividir por ella.)

El símbolo

$\ Pm \ sqrt {b ^ 2-4ac}$

en la fórmula debe entenderse como "cualquiera de los dos elementos cuyo cuadrado es

$b ^ 2-4ac, \,$

si existen tales elementos. En algunos campos, algunos elementos no tienen raíces cuadradas y algunos tienen dos; sólo zero es sólo una raíz cuadrada, excepto en los campos de la característica 2. Tenga en cuenta que incluso si un campo no contiene una raíz cuadrada de un número, siempre hay una cuadrática campo de extensión que hace, por lo que la fórmula cuadrática siempre tendrá sentido como una fórmula en ese campo de extensión.

Característica 2

En un campo de característica 2, la fórmula cuadrática, que se basa en 2 siendo una unidad, no se sostiene. Considera el polinomio cuadrático monic

$\ Displaystyle x ^ {2} + bx + c$

sobre un campo de característica 2. Si b = 0, entonces la solución se reduce a la extracción de una raíz cuadrada, por lo que la solución es

$\ Displaystyle x = \ sqrt {c}$

y tenga en cuenta que sólo hay una raíz desde

$\ Displaystyle - \ sqrt {c} = - \ sqrt {c} + 2 \ sqrt {c} = \ sqrt {c}.$

En resumen,

$\ Displaystyle x ^ {2} + c = (x + \ sqrt {c}) ^ {2}.$

Ver residuo cuadrático para obtener más información acerca de cómo extraer raíces cuadradas en campos finitos.

En el caso de que b ≠ 0, existen dos raíces distintas, pero si el polinomio es irreductible, no se puede expresar en términos de raíces cuadradas de números en el campo coeficiente. En su lugar, definir el R-2 raíz (c) de c ser una raíz del polinomio x ² + x + c, un elemento de la campo de la división de ese polinomio. Una verifica que R (c) + 1 es también una raíz. En términos de la operación 2-raíz, las dos raíces de la (no monic) hacha cuadrática ² + bx + c son

$\ Frac {b} {a} R \ left (\ frac {ac} {b ^ 2} \ right)$

$\ Frac {b} {a} \ left (R \ left (\ frac {ac} {b ^ 2} \ right) 1 \ right).$

Por ejemplo, permitir que un denotan un generador multiplicativo del grupo de unidades de F _4, la Galois campo de orden cuatro (así una y un + 1 son raíces de x ² + x + 1 más de F _4). Debido a que (a + 1) ² = a, a + 1 es la solución única de la ecuación cuadrática x ² + a = 0. Por otra parte, el polinomio x + ax + 1 es irreducible sobre F _4, pero se divide sobre F _16, donde se ha las dos raíces ab y AB + a, donde b es una raíz de x ² + x + a en F _16.

Este es un caso especial de Teoría Artin-Schreier.

Libro

Védicos Matemáticas: Dieciséis simple fórmulas matemáticas de los Vedas, por Swami Sankaracarya (1884-1960), Motilal Banarsidass Indological Editores y Libreros, Varnasi, India, 1965; reimpreso en Delhi, India, 1975, 1978. 367 páginas.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Quadratic_equation&oldid=199164119 "