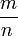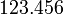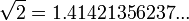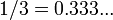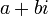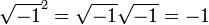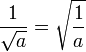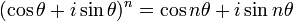Número
Antecedentes de las escuelas de Wikipedia
Este contenido de Wikipedia ha sido seleccionada por SOS para su utilización en las escuelas de todo el mundo. patrocinio SOS Niño es cool!
Un número es una objeto abstracto, fichas de los cuales son símbolos utilizados en contar y medir . Un símbolo que representa un número se llama una numeral, pero en el uso común se utiliza el número de palabra tanto para el objeto abstracto y el símbolo. Además de su uso en el conteo y medición, los números se utilizan a menudo para las etiquetas ( números de teléfono), por pedido ( números de serie), y para los códigos ( Los ISBN). En matemáticas , la definición de número se ha ampliado en los últimos años para incluir los números tales como cero , los números negativos , números racionales , números irracionales y números complejos .
Ciertos procedimientos de entrada uno o más números y salida a un número se llaman numérica operaciones. Entrada operaciones Unario un solo número y la salida de un solo número. Por ejemplo, la operación sucesor añade uno a un número entero: el sucesor de 4 es 5. más comunes son operaciones binarias que dos números de entrada y salida de un único número. Ejemplos de operaciones binarias incluyen además , resta , multiplicación , división y exponenciación . El estudio de las operaciones numéricas se llama aritmética .
La rama de las matemáticas que estudia los sistemas de números abstractos tales como grupos , anillos y campos se llama álgebra abstracta .
Tipos de números
Los números se pueden clasificar en conjuntos, llamados sistemas numéricos . (Para los diferentes métodos de expresar números con símbolos, como los números romanos , ver sistemas de numeración .)
Números naturales
Los números más conocidos son los números naturales o números de contar: uno, dos, tres, .... Algunas personas también incluyen cero en los números naturales; sin embargo, otros no lo hacen.
En la base diez sistema numérico, en uso casi universal hoy para operaciones aritméticas, los símbolos para los números naturales se escriben utilizando diez dígitos : 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. En este sistema de base diez, el dígito más a la derecha de un número natural tiene un valor de posición de uno, y cada otro dígito tiene un valor posicional diez veces mayor que la del valor posicional del dígito a su derecha. El símbolo para el conjunto de todos los números naturales es N, también escrito 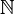 .
.
Enteros
Los números negativos son números que son menos que cero. Ellos son lo contrario de los números positivos. Por ejemplo, si un número positivo indica un depósito bancario, a continuación, un número negativo indica una retirada de la misma cantidad. Los números negativos se escriben normalmente escribiendo un signo negativo delante del número que son lo contrario de. Así, el opuesto de 7 está escrito -7. Cuando el juego de los opuestos de los números naturales se combina con los números naturales y el cero, se obtienen los números enteros Z (alemán Zahl, plural Zahlen), también escriben 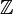 .
.
Numeros racionales
Un número racional es un número que puede ser expresado como una fracción con un número entero numerador y un número natural distinto de cero denominador . La fracción m / n o
m representa partes iguales, donde las piezas n iguales de ese tamaño conforman un todo. Dos fracciones diferentes pueden corresponder al mismo número racional; por ejemplo 1/2 y 2/4 son iguales, es decir:
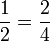 .
.
Si el valor absoluto de m es mayor que n, entonces el valor absoluto de la fracción es mayor que 1. Las fracciones que puede ser mayor que, menor que, o igual a 1 y también puede ser positivo, negativo o cero. El conjunto de todas las fracciones incluye los enteros, ya que cada número entero puede ser escrito como una fracción con denominador 1. Por ejemplo -7 puede ser escrito -7/1. El símbolo de los números racionales es Q (por cociente), también por escrito 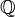 .
.
Los números reales
Los números reales incluyen todos los números de medición. Los números reales se escriben generalmente usando decimales números, en el que el punto decimal se coloca a la derecha del dígito con el lugar de valor uno. Después del punto decimal, cada dígito tiene un valor posicional de un décimo del valor posicional del dígito a su izquierda. Así
representa 1 cien, 2, 3 decenas queridos, 4/10, 5/100 y 6/1000. Al decir el número, el decimal se lee "punto", por lo tanto: "uno dos tres cuatro cinco seis puntos". En, por ejemplo, los EE.UU. y el Reino Unido, el decimal se representa por una período, en Europa continental por un coma. Cero se escribe a menudo como 0.0 y negativos números reales se escriben con un precedente signo menos:
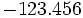 .
.
Cada número racional también es un número real. Para escribir una fracción como un decimal, divide el numerador entre el denominador. No es el caso, sin embargo, que todo número real es racional. Si un número real no se puede escribir como una fracción de dos números enteros, se llama irracional . Un decimal que se puede escribir como una fracción cualquiera extremos (termina) o para siempre repite, porque es la respuesta a un problema en la división. Así, el número real 0.5 se puede escribir como medio y el número real 0,333 ... (tres en tres para siempre de repetición) se puede escribir como 1/3. Por otro lado, el número real π ( pi ), la relación de la circunferencia de cualquier círculo a su diámetro , es
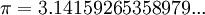 .
.
Dado que el decimal ni termina ni se repite siempre, no se puede escribir como una fracción, y es un ejemplo de un número irracional. Otros números irracionales incluyen
(La raíz cuadrada de 2, es decir, el número positivo cuyo cuadrado es 2).
Del mismo modo que las fracciones se pueden escribir en más de una forma, también lo puede decimales. Por ejemplo, si multiplicamos ambos lados de la ecuación
por tres, descubrimos que
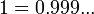 .
.
Por lo tanto 1,0 y 0.999 ... son dos números decimales diferentes que representan el número natural 1. Hay infinitamente muchas otras formas de representar el número 1, por ejemplo 2/2, 3/3, 1.00, 1.000, y así sucesivamente.
Cada número real es ya sea racional o irracional. Cada número real corresponde a un punto en el numero de linea. Los números reales también tienen un importante pero muy técnico propiedad llamada la propiedad del límite superior menos. El símbolo de los números reales es R o  .
.
Cuando un número real representa una medición , siempre hay un margen de error . Esto a menudo se indica mediante redondeo o truncando un decimal, por lo que los dígitos que sugieren una precisión mayor que la medición en sí se eliminan. Los dígitos restantes son llamados dígitos significativos. Por ejemplo, las mediciones con una regla rara vez se pueden hacer sin un margen de error de al menos 0,01 metros. Si los lados de una rectángulo se mide como 1.23 metros y 4.56 metros, entonces la multiplicación da un espacio para el rectángulo de 5.6088 metros cuadrados. Dado que sólo los primeros dos dígitos después del punto decimal son significativos, esto normalmente se redondea a 5,61.
En álgebra abstracta , los números reales se caracterizan únicamente por ser el único completamente ordenado campo. No son, sin embargo, una algebraicamente cerrado.
Los números complejos
Mudarse a un mayor nivel de abstracción, los números reales pueden ser extendidos a los números complejos . Este conjunto de números se levantó, históricamente, desde la cuestión de si un número negativo puede tener una raíz cuadrada . Esto llevó a la invención de un nuevo número: la raíz cuadrada de un negativo, denotada por i , un símbolo asignado por Leonhard Euler , y llamó a la unidad imaginaria . Los números complejos se componen de todos los números de la forma
donde a y b son números reales. En la expresión a + bi, el número real a se llama la parte real y bi se llama la parte imaginaria. Si la parte real de un número complejo es cero, entonces el número se llama número imaginario o que se conoce como puramente imaginario; si la parte imaginaria es cero, entonces el número es un número real. Por lo tanto los números reales son un subconjunto de los números complejos. Si las partes real e imaginaria de un número complejo son ambos enteros, a continuación, el número se llama Número entero de Gauss. El símbolo para los números complejos es C o  .
.
En álgebra abstracta , los números complejos son un ejemplo de un algebraicamente cerrado, lo que significa que cada polinomio con el complejo coeficientes pueden ser factorizados en factores lineales. Al igual que el sistema de números reales, el sistema de números complejos es un campo y es completa, pero a diferencia de los números reales no es ordenada. Es decir, no hay un significado al decir que i es mayor que 1, ni hay ningún significado en decir que que i es inferior a 1. En términos técnicos, los números complejos no tienen la propiedad de tricotomía .
Los números complejos corresponden a puntos en el plano complejo , a veces llamado el plano de Argand.
Cada uno de los sistemas numéricos mencionado anteriormente es un subconjunto propio de la siguiente sistema de numeración. Simbólicamente, N ⊂ Z ⊂ Q ⊂ R ⊂ C.
Otros tipos
Superreal, hiperreal y números surreales extienden los números reales mediante la adición de infinitesimalmente pequeños números y infinitamente grandes números, pero siguen formando campos.
La idea detrás de p-adic números es esto: en que los números reales pueden tener expansiones infinitamente largas a la derecha del punto decimal, estos números permitir infinitamente largas expansiones a la izquierda. El sistema numérico que resulta depende de lo base se utiliza para los dígitos: cualquier base es posible, pero se obtiene un sistema con las mejores propiedades matemáticas cuando la base es un número primo .
Para hacer frente a los conjuntos infinitos, los números naturales se han generalizado a los números ordinales y los números cardinales . El primero da el orden de la colección, mientras que el segundo da su tamaño. Para el conjunto finito, los números ordinales y cardinales son equivalentes, pero difieren en el caso infinito.
Hay también otros conjuntos de números con usos especializados. Algunos son subconjuntos de los números complejos. Por ejemplo, números algebraicos son las raíces de polinomios con racional coeficientes. Los números complejos que no son algebraicos se llaman números trascendentes.
Juegos de números que no son subconjuntos de los números complejos a veces se llaman números hipercomplejos. Estos incluyen el cuaterniones H, inventado por Sir William Rowan Hamilton, en el que la multiplicación no es conmutativa , y el octoniones, en el que la multiplicación no es asociativa . Elementos de campos de funciones de no-cero comportan característica en algunos aspectos como los números y son a menudo considerados como números de teoría de números.
Números
Los números deben ser distinguidos de números, los símbolos utilizados para representar números. El número cinco se puede representar por tanto la base de diez numeral '5' y por el número romano 'V'. Anotaciones usadas para representar números se discuten en el artículo sistemas de numeración . Un hecho importante en la historia de los números fue el desarrollo de un sistema posicional, como decimales modernas, que pueden representar números muy grandes. Los números romanos requieren símbolos adicionales para números más grandes.
Historia
Historia de los números enteros
Los primeros números
Se especula que el primer uso conocido de los números se remonta a alrededor de 30.000 BC, huesos u otros artefactos han sido descubiertos con marcas de corte en los que a menudo se consideran marcas de conteo. El uso de estas marcas de conteo se han sugerido para ser cualquier cosa de contar el tiempo transcurrido, como el número de días, o llevar registros de las cantidades.
Sistemas de recuento no tienen el concepto de lugar-valor (como en la notación decimal actualmente en uso), que limitan su representación de los grandes números y, como tal, a menudo se considera que este es el primer tipo de sistema abstracto que se utilizaría, y podría ser considerado un sistema numeral.
El primer sistema conocido con el lugar-valor fue el Mesopotámica sistema de base 60 (ca. 3400 aC) y el sistema más antiguo conocido de base 10 fechas para 3100 aC en Egipto .
Historia de cero
El uso de cero como un número debe distinguirse de su uso como un marcador de posición en el numeral sistemas de valor posicional. Muchos textos indios antiguos utilizan una sánscrito palabra Shunya para referirse al concepto de vacío; en los textos de matemáticas de esta palabra a menudo se utiliza para referirse al número cero. . En una línea similar, Pāṇini ( Siglo quinto antes de Cristo) que se utiliza la (cero) operador nulo (es decir, un producción lambda) en el Ashtadhyayi, su gramática algebraica para el sánscrito idioma. (Véase también Pingala)
Los registros muestran que los antiguos griegos parecía seguro del estado de cero como un número: se preguntaron "¿cómo puede" nada "ser algo?" dando lugar a interesantes filosófica y, por el período medieval, los argumentos religiosos sobre la naturaleza y la existencia de cero y el vacío. La paradojas de Zenón de Elea dependen en gran medida de la interpretación incierta de cero. (Los antiguos griegos incluso cuestionaron si 1 era un número.)
Las finales olmecas gente de la zona centro-sur México comenzaron a utilizar un verdadero cero (un glifo cáscara) en el Nuevo Mundo, posiblemente, por la Siglo cuarto antes de Cristo, pero sin duda por 40 antes de Cristo, que se convirtió en una parte integral de Numeración maya y la Calendario Maya, pero no influyó en sistemas de numeración del Viejo Mundo.
Por 130, Ptolomeo , influenciado por Hiparco y los babilonios, estaba usando un símbolo para el cero (un pequeño círculo con una larga barra superior) dentro de un sistema de numeración sexagesimal de otra manera usar alfabético Numerales griegos. Debido a que se utiliza solo, no sólo como un marcador de posición, esta Cero helenístico fue el primer uso documentado de un cero real en el Viejo Mundo. En posteriores bizantinos manuscritos de su Syntaxis Mathematica (Almagesto), el cero helenístico se había transformado en la letra griega omicron (de lo contrario lo que significa 70).
Se utilizó otro cero cierto en mesas junto a los números romanos por 525 (primer uso conocido por Dionisio el Exiguo), sino como una palabra, nulla significa nada, no como un símbolo. Cuando división produjo cero como un resto, nihil, que también significa nada, se utilizó. Estos ceros medievales fueron utilizados por todos los futuros medieval computistas (calculadoras de Pascua ). Un uso aislado de su inicial, N, se utiliza en una tabla de números romanos por Bede o un colega acerca de 725, un verdadero símbolo cero.
Un uso temprano documentado del cero por Brahmagupta (en el Brahmasphutasiddhanta) data 628. Él trató cero como un número y las operaciones que implican que discuten, incluyendo división. Por esta época (siglo 7) el concepto había alcanzado claramente Camboya , y la documentación muestra la idea después se extiende a China, y la islámica mundial.
Historia de los números negativos
El concepto abstracto de los números negativos se reconoció ya en 100 aC - 50 antes de Cristo. Los chinos " Nueve capítulos del arte matemático "(Jiu zhang suanshu) contiene métodos para encontrar las áreas de figuras; barras rojas se utilizan para denotar positivo coeficientes, negro para el negativo. Esta es la primera mención conocida de los números negativos en el Este; la primera referencia en una obra occidental era en el siglo tercero en Grecia . Diofanto hace referencia a la ecuación equivalente a 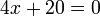 (La solución sería negativo) en Aritmética, diciendo que la ecuación dio un resultado absurdo.
(La solución sería negativo) en Aritmética, diciendo que la ecuación dio un resultado absurdo.
Durante el 600s, los números negativos estaban en uso en la India para representar deudas. Referencia anterior Diofanto fue discutido de forma más explícita por el matemático indio Brahmagupta, en Brahma-Sphuta-Siddhanta 628, que utiliza los números negativos para producir la forma general fórmula cuadrática que sigue en uso hoy en día. Sin embargo, en el siglo 12 en la India, Bhaskara da raíces negativas para ecuaciones de segundo grado, pero dice que el valor negativo "es que en este caso no debe ser tomado, porque es inadecuada, la gente no aprueban raíces negativas."
Europeos matemáticos, en su mayor parte, resistieron el concepto de números negativos hasta el siglo 17 , aunque Fibonacci permitió soluciones negativas en problemas financieros, donde podrían ser interpretadas como débitos (capítulo 13 del Ábacos de Liber, 1202) y más tarde como pérdidas (en Flos). Al mismo tiempo, los chinos estaban indicando los números negativos dibujando un trazo diagonal a través del dígito más a la derecha que no sea cero del numeral del número positivo correspondiente. El primer uso de números negativos en una obra europea era por Chuquet durante el siglo 15 . Los usó como exponentes , pero se refirió a ellos como "números absurdos".
Tan recientemente como en el siglo 18 , el suizo matemático Leonhard Euler cree que los números negativos fueron mayores que el infinito , y que era una práctica común para ignorar cualquier resultado negativo devueltos por ecuaciones en el supuesto de que no tenían sentido, al igual que René Descartes hizo con soluciones negativas en un sistema de coordenadas cartesianas .
Historia de los números racionales, irracionales y reales
Historia de los números racionales
Es probable que el concepto de los números fraccionarios data tiempos prehistóricos. Incluso el Los antiguos egipcios escribieron textos de matemáticas que describe cómo convertir generales fracciones en su notación especial. Matemáticos griegos e indios clásicos hicieron estudios de la teoría de los números racionales, como parte del estudio general de la teoría de números . El más conocido de ellos es los Elementos de Euclides , que data de más o menos 300 antes de Cristo. De los textos indios, el más relevante es el Sthananga Sutra, que también cubre la teoría de números como parte de un estudio general de las matemáticas.
El concepto de las fracciones decimales está estrechamente vinculada con la notación de valor decimal; los dos parecen haber desarrollado en tándem. Por ejemplo, es común que los sutras matemáticas jainistas que incluyen cálculos de aproximaciones decimales de fracciones a pi o el raíz cuadrada de dos. Del mismo modo, los textos de matemáticas babilónicas siempre habían utilizado fracciones sexagesimales con gran frecuencia.
Historia de los números irracionales
El primer uso conocido de los números irracionales estaba en el Índico Sulba Sutras compuestos entre 800- 500 antes de Cristo. Las primeras pruebas de existencia de los números irracionales se suele atribuir a Pitágoras , más específicamente a la Pitagórico Hipaso de Metaponto, que produjo una (muy probablemente geométrica) prueba de la irracionalidad de la raíz cuadrada de 2. La historia cuenta que Hípaso descubrió números irracionales cuando se trata de representar a la raíz cuadrada de 2 como una fracción. Sin embargo Pitágoras creía en lo absoluto de los números, y no podía aceptar la existencia de los números irracionales. No podía refutar su existencia a través de la lógica, pero sus creencias no aceptaría la existencia de los números irracionales y por eso condenado Hípaso a muerte por ahogamiento.
El siglo XVI vio la aceptación final por parte de los europeos negativos , integral y fraccionarios números. El siglo XVII vio fracciones decimales con la notación moderna utiliza bastante en general por los matemáticos. Pero no fue hasta el siglo XIX que los irracionales fueron separados en partes algebraicas y trascendentes, y un estudio científico de la teoría de los irracionales se toma una vez más. Había permanecido casi inactivo desde Euclides . El año 1872 vio la publicación de las teorías de Karl Weierstrass (por su alumno Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), y Richard Dedekind. Meray había tomado en 1869 el mismo punto de partida, Heine, pero la teoría se denomina generalmente el año 1872. método de Weierstrass ha sido completamente establecido por Salvatore Pincherle (1880), y Dedekind ha recibido prominencia adicional a través de la obra del autor más tarde (1888) y la reciente aprobación por parte de Paul Curtiduría (1894). Weierstrass, Cantor y Heine basan sus teorías en las series infinitas, mientras que Dedekind funda su en la idea de un cortar (schnitt) en el sistema de los números reales , separando todos los números racionales en dos grupos que tienen ciertas propiedades características. El sujeto ha recibido contribuciones posteriores a manos de Weierstrass, Kronecker (Crelle, 101), y Meray.
Fracciones continuas, estrechamente relacionados con los números irracionales (y debido a Cataldi, 1613), recibieron atención por parte de Euler , y en la apertura del siglo XIX trajeron a la prominencia a través de los escritos de Joseph Louis Lagrange . Otros notables contribuciones han sido hechas por Druckenmüller (1837), Kunze (1857), Lemke (1870), y Günther (1872). Ramus (1855) primero conecta el tema con determinantes , dando como resultado, con las aportaciones posteriores de Heine, Möbius, y Günther, en la teoría de Kettenbruchdeterminanten. Dirichlet también añadido a la teoría general, al igual que numerosos contribuyentes a las aplicaciones de la asignatura.
Números trascendentes y reales
Los primeros resultados relativos a los números trascendentes fueron 1761 prueba de Lambert que π no puede ser racional, y también que e n es irracional si n es racional (a menos que n = 0). (La constante e fue convocado por primera vez en 1618 la obra de Napier sobre logaritmos .) Legendre extendió esta prueba demostró que π no es la raíz cuadrada de un número racional. La búsqueda de las raíces de quinto grado y ecuaciones de grado superior fue un importante desarrollo, la Teorema de Abel-Ruffini ( Ruffini 1799, Abel 1824) mostró que no podían ser resueltos por radicales (fórmula que incluyan únicamente las operaciones aritméticas y raíces). Por lo tanto, era necesario considerar el conjunto más amplio de números algebraicos (todos soluciones a las ecuaciones polinómicas). Galois (1832) vinculado ecuaciones polinómicas de la teoría de grupos que da lugar al campo de la teoría de Galois .
Incluso el conjunto de números algebraicos no era suficiente y todo el conjunto de los números reales incluye números trascendentes. La existencia de la cual se estableció por primera vez por Liouville (1844, 1851). Hermite demostró en 1873 que e es trascendental y Lindemann demostró en 1882 que π es trascendental. Finalmente Cantor muestra que el conjunto de todos los números reales es uncountably infinita, pero el conjunto de todos números algebraicos es infinito numerable, por lo que hay un número infinito de uncountably números trascendentes.
Infinito
La concepción antigua que se conoce de matemática infinito aparece en la Yajur Veda, que en un momento dice "si se quita una parte del infinito o añade una parte al infinito, aún lo que queda es infinito". Infinito era un tema popular de estudio filosófico entre la Jain matemáticos circa 400 antes de Cristo. Ellos distinguen entre cinco tipos de infinito: infinitas en una y dos direcciones, infinitos en la zona, infinito en todas partes, y la infinita perpetuamente.
En Occidente, la noción tradicional del infinito matemático fue definida por Aristóteles , quien distingue entre infinito actual y el infinito potencial; el consenso general es que sólo este último tenía verdadero valor. Galileo 's Dos nuevas ciencias discutieron la idea de uno-a-uno correspondencia entre conjuntos infinitos. Pero el siguiente avance importante en la teoría fue hecha por Georg Cantor ; en 1895 publicó un libro sobre su nueva teoría de conjuntos , por el que, entre otras cosas, la hipótesis del continuo.
Una versión geométrica moderna del infinito está dada por la geometría proyectiva, que introduce "puntos ideales en el infinito", uno para cada dirección espacial. Cada familia de líneas paralelas en una dirección dada se postula a converger en el punto ideal correspondiente. Esto está estrechamente relacionado con la idea de puntos de fuga en dibujo en perspectiva.
Los números complejos
La referencia más temprana fugaz de raíces cuadradas de números negativos se produjo en la obra del matemático e inventor Herón de Alejandría en el siglo 1 dC, cuando se considera el volumen de un imposible tronco de pirámide . Se volvieron más prominentes cuando en el siglo 16 cerrado fórmulas para las raíces de polinomios tercero y cuarto grado fueron descubiertos por los matemáticos italianos (ver Niccolo Fontana Tartaglia, Gerolamo Cardano). Pronto se dio cuenta de que estas fórmulas, incluso si uno sólo estaba interesado en soluciones reales, a veces requieren la manipulación de las raíces cuadradas de números negativos.
Esto fue doblemente inquietante ya que ni siquiera consideraron números negativos para estar en tierra firme en el momento. El término "imaginario" para estas cantidades fue acuñado por René Descartes en 1637 y estaba destinado a ser despectivo (ver número imaginario para una discusión de la "realidad" de los números complejos). Otra fuente de confusión es que la ecuación
parecía ser caprichosamente incompatible con la identidad algebraica
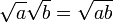 ,
,
que es válido para los positivos números reales a y b, y que también se utilizó en cálculos con números complejos con uno de a, b positivo y el otro negativo. El uso incorrecto de esta identidad, y la identidad relacionados
en el caso de que tanto a como b son negativos incluso acosado Euler . Esta dificultad eventualmente lo llevó a la convención de usar el símbolo especial i en lugar de √-1 para evitar este error.
El siglo 18 vio los trabajos de Abraham de Moivre y Leonhard Euler . Para Moivre es debido (1730) la conocida fórmula que lleva su nombre, fórmula de De Moivre:
y Euler (1748) La fórmula de Euler de análisis complejo:
La existencia de los números complejos no fue completamente aceptada hasta la interpretación geométrica había sido descrito por Caspar Wessel en 1799 ; fue redescubierto varios años más tarde y popularizado por Carl Friedrich Gauss , y como resultado la teoría de los números complejos recibió una notable expansión. La idea de la representación gráfica de los números complejos había aparecido, sin embargo, ya en 1685, en Tractatus de Álgebra de Wallis.
También en 1799, Gauss proporcionó la primera prueba generalmente aceptada de la teorema fundamental del álgebra, mostrando que todo polinomio sobre los números complejos tiene un conjunto completo de soluciones en ese reino. La aceptación general de la teoría de los números complejos no es un poco debido a los trabajos de Augustin Louis Cauchy y Niels Henrik Abel, y sobre todo este último, que fue el primero en utilizar audazmente los números complejos con un éxito que es bien conocida.
Gauss estudió números complejos de la forma a + bi, donde a y b son integral, o racional (y i es una de las dos raíces de x 2 + 1 = 0). Su alumno, Ferdinand Eisenstein, estudió el tipo a + bω, donde ω es una raíz compleja de x 3-1 = 0. Otros dichas clases (llamado campos ciclotómicos) de números complejos se derivan de la raíces de la unidad x k - 1 = 0 para los valores más altos de k. Esta generalización se debe principalmente a Ernst Kummer, quien también inventó números ideales, que se expresaron como entidades geométricas por Felix Klein en 1893. La teoría general de campos fue creado por Evariste Galois, que estudió los campos generados por las raíces de cualquier ecuación polinómica F (x) = 0.
En 1850 Víctor Alexandre Puiseux dio el paso clave de distinguir entre los postes y los puntos de ramificación, e introdujo el concepto de puntos singulares esenciales; esto llevaría finalmente al concepto de la extendido plano complejo.
Números primos
Los números primos se han estudiado a lo largo de la historia registrada. Euclides dedicó un libro de los elementos a la teoría de los números primos; en ella demostró la infinitud de los números primos y el teorema fundamental de la aritmética , y presentó el Algoritmo de Euclides para hallar el máximo común divisor de dos números.
En 240 aC, Eratóstenes utilizó el Criba de Eratóstenes para aislar rápidamente los números primos. Pero la mayor perfeccionamiento de la teoría de los números primos en Europa data del Renacimiento y épocas posteriores.
En 1796 , Adrien-Marie Legendre conjeturó el teorema de los números primos, que describe la distribución asintótica de los números primos. Otros resultados sobre la distribución de los números primos incluyen demostración de Euler que la suma de los inversos de los primos diverge, y la conjetura de Goldbach que afirma que cualquier número par suficientemente grande es la suma de dos números primos. Sin embargo, otra conjetura relacionada con la distribución de los números primos es el Hipótesis de Riemann, formulado por Bernhard Riemann en 1859 . El teorema del número primo fue finalmente probado por Jacques Hadamard y Charles de la Vallée-Poussin en 1896 .