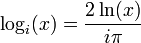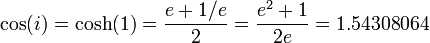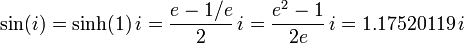Unidad imaginaria
Antecedentes de las escuelas de Wikipedia
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. El apadrinamiento de niños ayuda a los niños uno por uno http://www.sponsor-a-child.org.uk/ .
En matemáticas, la física y la ingeniería, la unidad imaginaria se denota por 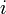 o el América
o el América 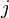 o el griego iota (ver notaciones alternativas a continuación). Permite que el número real del sistema,
o el griego iota (ver notaciones alternativas a continuación). Permite que el número real del sistema, 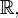 que se extienda a la número complejo sistema,
que se extienda a la número complejo sistema, 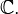 Su definición precisa depende del método particular de extensión.
Su definición precisa depende del método particular de extensión.
La principal motivación para esta extensión es el hecho de que no todos los ecuación polinómica con coeficientes reales 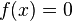 tiene una solución en los números reales. En particular, la ecuación
tiene una solución en los números reales. En particular, la ecuación 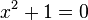 no tiene solución real (véase "Definición", más abajo). Sin embargo, si permitimos que los números complejos como soluciones, entonces esta ecuación, y de hecho toda ecuación polinómica
no tiene solución real (véase "Definición", más abajo). Sin embargo, si permitimos que los números complejos como soluciones, entonces esta ecuación, y de hecho toda ecuación polinómica 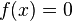 no tener una solución. (Ver clausura algebraica y teorema fundamental del álgebra.)
no tener una solución. (Ver clausura algebraica y teorema fundamental del álgebra.)
Para una historia de la unidad imaginaria, ver la historia de los números complejos .
La unidad imaginaria a menudo se refiere vagamente como la "raíz cuadrada de un negativo" o la "raíz cuadrada de menos uno", pero a continuación encontrará dificultades que pueden surgir a partir de un uso ingenuo de esta idea.
Definición
Por definición, la unidad imaginaria  es una solución (de dos) de la ecuación cuadrática
es una solución (de dos) de la ecuación cuadrática
o equivalentemente
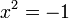 .
.
Dado que no hay ningún número real que produce un número real negativo al cuadrado, nos imaginamos un número tal y asignamos el símbolo i. Es importante tener en cuenta, sin embargo, que i es así definidos por una construcción matemática como los números reales, a pesar de su nombre formal y ser menos inmediatamente intuitiva.
Operaciones de números reales se pueden extender a los números imaginarios y complejos mediante el tratamiento de i como una cantidad desconocida al manipular una expresión, y luego utilizando la definición de reemplazar cualquier aparición de i 2 con -1. Poderes Superior integrales de  También puede ser reemplazado con - i, 1,
También puede ser reemplazado con - i, 1,  , O -1:
, O -1:
 y -
y - 
Ser un polinomio de segundo orden sin verdadera raíz múltiple, la ecuación anterior tiene dos soluciones distintas que son igualmente válidas y que pasan a ser aditivo y inversos multiplicativos de la otra. Más precisamente, una vez una solución de  de la ecuación ha sido fijado, el valor -
de la ecuación ha sido fijado, el valor -  (Que no es igual a
(Que no es igual a  ) Es también una solución. Como la ecuación es la única definición de
) Es también una solución. Como la ecuación es la única definición de  , Parece que la definición es ambigua (más precisamente, no bien definido). Sin embargo, hay ambigüedad resulta siempre que una de las soluciones que se elija y se fija como "positivo
, Parece que la definición es ambigua (más precisamente, no bien definido). Sin embargo, hay ambigüedad resulta siempre que una de las soluciones que se elija y se fija como "positivo  . "Esto se debe a que, aunque -
. "Esto se debe a que, aunque -  y
y  no son cuantitativamente equivalente (que son negativos de cada uno), no hay diferencia cualitativa entre
no son cuantitativamente equivalente (que son negativos de cada uno), no hay diferencia cualitativa entre  y -
y -  (Que no puede decirse de -1 y 1). Ambos números imaginarios tienen el mismo derecho a ser el número cuyo cuadrado es -1. Si todos los libros de texto de matemáticas y literatura publicada en referencia a los números imaginarios o complejas fueron reescritos con -
(Que no puede decirse de -1 y 1). Ambos números imaginarios tienen el mismo derecho a ser el número cuyo cuadrado es -1. Si todos los libros de texto de matemáticas y literatura publicada en referencia a los números imaginarios o complejas fueron reescritos con -  reemplazar todas las apariciones de +
reemplazar todas las apariciones de +  (Y por lo tanto todas las apariciones de -
(Y por lo tanto todas las apariciones de -  reemplazado por - (-
reemplazado por - (-  ) = +
) = +  ), Todos los hechos y teoremas seguirían siendo equivalente válido. La distinción entre las dos raíces
), Todos los hechos y teoremas seguirían siendo equivalente válido. La distinción entre las dos raíces 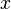 de
de 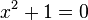 con uno de ellos como "positivo" es puramente una reliquia de notación; ni raíz puede decirse que es más primaria o fundamental que el otro.
con uno de ellos como "positivo" es puramente una reliquia de notación; ni raíz puede decirse que es más primaria o fundamental que el otro.
El problema puede ser muy sutil. La explicación más precisa es decir que, aunque el complejo campo, definido como R [X] / (X 2 + 1), (ver número complejo ) es único hasta isomorfismo, no es única hasta un isomorfismo único - hay exactamente 2 automorfismos de campo de R [X] / (X 2 + 1), la identidad y el automorfismo enviando X - X. (Estos no son los automorfismos único campo de C, pero son los únicos automorfismos de campo de C que mantienen a cada número real fijo.) Ver número complejo , conjugación compleja, campo automorfismo, y Grupo de Galois.
Un problema similar surge si los números complejos se interpretan como 2 × 2 reales matrices (véase el número complejo ), porque entonces tanto
y
son soluciones a la ecuación matricial
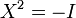 .
.
En este caso, la ambigüedad resulta de la elección geométrica de los cuales "dirección" alrededor de la círculo unidad es la rotación de "positiva". Una explicación más preciso es decir que la grupo de automorfismos de los grupo especial ortogonal SO (2, R) tiene exactamente 2 elementos - la identidad y el automorfismo que intercambia "CW" (a la derecha) y rotaciones "CCW" (hacia la izquierda). Ver grupo ortogonal.
Todas estas ambigüedades pueden resolverse mediante la adopción de una forma más rigurosa definición de número complejo , y explícitamente la elección de una de las soluciones de la ecuación para ser la unidad imaginaria. Por ejemplo, el par ordenado (0, 1), en la construcción habitual de los números complejos con vectores bidimensionales.
El uso adecuado
La unidad imaginaria se escribe a veces 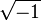 en contextos avanzados de matemáticas (así como en los textos populares menos avanzados); Sin embargo, el gran cuidado debe tomarse al manipular fórmulas que impliquen radicales. La notación es reservado, ya sea para el principal de la raíz cuadrada de la función, que sólo se define de verdad
en contextos avanzados de matemáticas (así como en los textos populares menos avanzados); Sin embargo, el gran cuidado debe tomarse al manipular fórmulas que impliquen radicales. La notación es reservado, ya sea para el principal de la raíz cuadrada de la función, que sólo se define de verdad 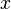 ≥ 0, o de la rama principal del complejo función de raíz cuadrada. El intento de aplicar las reglas de cálculo de la capital (real) función de raíz cuadrada para manipular la rama principal del complejo de la función raíz cuadrada producirá resultados falsos:
≥ 0, o de la rama principal del complejo función de raíz cuadrada. El intento de aplicar las reglas de cálculo de la capital (real) función de raíz cuadrada para manipular la rama principal del complejo de la función raíz cuadrada producirá resultados falsos:
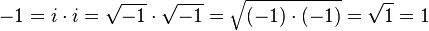 (Incorrecta)
(Incorrecta)
La regla de cálculo
sólo es válido para los valores reales, no negativos de 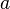 y
y 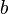 .
.
Para una discusión más a fondo de este fenómeno, ver raíz cuadrada y rama.
Para evitar cometer este tipo de errores en la manipulación de los números complejos, una estrategia nunca es utilizar un número negativo bajo un signo de la raíz cuadrada. Por ejemplo, en lugar de escribir expresiones como  , Se debe escribir
, Se debe escribir 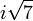 en su lugar. Ese es el uso para el que fue creada la unidad imaginaria.
en su lugar. Ese es el uso para el que fue creada la unidad imaginaria.
Raíz cuadrada de la unidad imaginaria
Uno podría suponer que necesitamos una nueva serie de números imaginarios que inventar para dar cuenta de la raíz cuadrada de i. Sin embargo esto no es necesario, ya que puede ser expresada (aunque bastante mal - véase más arriba), ya sea como de dos números complejos:
Esto puede demostrarse que es válida desde:
Poderes de 
Los poderes de  repetir en un ciclo:
repetir en un ciclo:
Esto puede ser expresado con el siguiente patrón donde n es cualquier número entero:
Esto lleva a la conclusión de que
i y la fórmula de Euler
La fórmula de Euler es
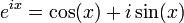 ,
,
donde x es un número real. La fórmula también se puede extender para analíticamente complejo x.
Sustituyendo  rendimientos
rendimientos
y se llega a la elegante identidad de Euler :
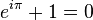 .
.
Este notable simple ecuación relaciona cinco cantidades matemáticas significativas (0, 1, π, e, i) por medio de las operaciones básicas de suma, multiplicación y exponenciación.
Ejemplo
La sustitución de 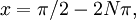 donde N es un número entero arbitrario, produce
donde N es un número entero arbitrario, produce
O, levantando cada lado para el poder  ,
,
o
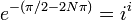 ,
,
lo que demuestra que 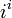 tiene un número infinito de elementos en forma de
tiene un número infinito de elementos en forma de
donde n es cualquier número entero. Este valor real aunque real no se determina de forma única. La razón es que la logaritmo complejo es multiplicar con valores.
Operaciones con i
Muchas operaciones matemáticas que se pueden llevar a cabo con números reales también se pueden llevar a cabo con  , Como exponentation, raíces, logaritmos y funciones trigonométricas.
, Como exponentation, raíces, logaritmos y funciones trigonométricas.
Un número elevado a la 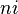 de potencia es:
de potencia es:
La 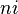 º raíz de un número es:
º raíz de un número es:
La log i la base de un número es:
El coseno de  es un número real:
es un número real:
Y el seno del  es imaginario:
es imaginario:
Notaciones alternativas
- En ingeniería eléctrica y campos relacionados, la unidad imaginaria se escribe a menudo como
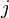 para evitar la confusión con corriente eléctrica como una función del tiempo, tradicionalmente denota por
para evitar la confusión con corriente eléctrica como una función del tiempo, tradicionalmente denota por 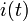 o solo
o solo 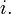 El lenguaje de programación Python también utiliza para denotar j la unidad imaginaria, mientras que en Matlab, ambas anotaciones iyj están asociadas a la unidad imaginaria.
El lenguaje de programación Python también utiliza para denotar j la unidad imaginaria, mientras que en Matlab, ambas anotaciones iyj están asociadas a la unidad imaginaria. - Algunos cuidado especial debe ser tomado en ciertos libros de texto que definen j = - i, en particular a las ondas que viajan (por ejemplo, un derecho de viajar onda plana en la dirección x
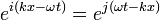 ).
). - Algunos textos utilizan la letra griega iota (ι) para escribir la unidad imaginaria para evitar confusiones. Por ejemplo: Biquaternion.
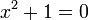
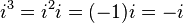
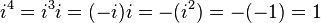
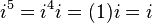
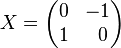
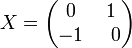
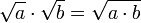
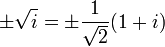
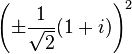
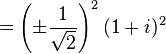
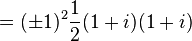
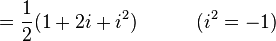
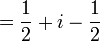

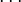
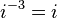
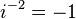
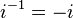
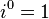
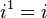
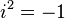
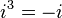
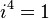
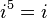
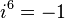
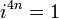
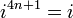
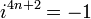
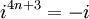
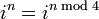
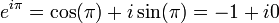

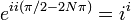
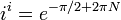
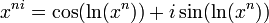
![! \ \ \ Sqrt [ni] {x} = \ cos (\ ln (\ sqrt [n] {x})) - i \ sin (\ ln (\ sqrt [n] {x}))](../../images/218/21805.png)