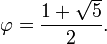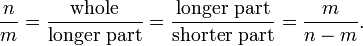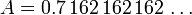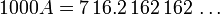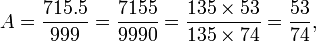Numero irracional

En las matem??ticas , un n??mero irracional es cualquier n??mero real que no es un n??mero racional - es decir, es un n??mero que no puede ser expresado como una fracci??n m / n, donde m y n son n??meros enteros , con n diferente de cero. De manera informal, esto significa n??meros que no pueden ser representados como fracciones simples. Se puede deducir que tampoco se pueden representar como terminaci??n o decimales peri??dicos, pero la idea es m??s profundo que eso. Si bien puede parecer extra??o a primera vista, casi todos los n??meros reales son irracionales, en un sentido que se define con mayor precisi??n a continuaci??n. Tal vez los n??meros m??s conocidos son irracional π y √2.

Cuando el raz??n entre las longitudes de dos segmentos de l??nea es irracional, los segmentos de l??nea tambi??n se describen como inconmensurable, lo que significa que comparten ninguna medida en com??n. Una medida de un segmento de l??nea I en este sentido es un segmento de l??nea J que "las medidas" I en el sentido de que toda alg??n n??mero de copias de J establecidas de extremo a extremo ocupan la misma longitud que I.

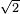El n??mero es irracional.

Historia

La primera prueba de la existencia de los n??meros irracionales se suele atribuir a Hipaso de Metaponto, un Pit??goras que probablemente les descubierto mientras se identifican lados de la pentagrama. Sin embargo Pit??goras cre??a en lo absoluto de los n??meros, y no pod??a aceptar la existencia de los n??meros irracionales. No pod??a refutar su existencia a trav??s de la l??gica, pero sus creencias no aceptar??a la existencia de los n??meros irracionales y por eso, como dice la leyenda ten??a, ten??a H??paso ahog??. Teodoro de Cirene demostr?? la irracionalidad de la irracionales de n??meros enteros hasta 17, pero se detuvo all?? probablemente porque el ??lgebra que utiliz?? no pod??a aplicarse a la ra??z cuadrada de 17. No fue hasta Eudoxo desarroll?? una teor??a de las relaciones irracionales que se cre?? una s??lida base matem??tica de los n??meros irracionales. Elementos de Euclides Libro 10 est?? dedicado a la clasificaci??n de las magnitudes irracionales.

El siglo XVI vio la aceptaci??n de los negativos , integrales y fraccionarios n??meros. El siglo XVII vio fracciones decimales con la notaci??n moderna utiliza bastante en general por los matem??ticos. Los pr??ximos cien a??os vieron los n??meros imaginarios se convierten en una herramienta poderosa en manos de Abraham de Moivre, y especialmente de Leonhard Euler . La finalizaci??n de la teor??a de los n??meros complejos en el siglo XIX supuso la diferenciaci??n de los irracionales en n??meros algebraicos y trascendentes, la prueba de la existencia de n??meros trascendentes, y el resurgimiento del estudio cient??fico de la teor??a de los irracionales, en gran parte ignorados desde Euclides . El a??o 1872 vio la publicaci??n de las teor??as de Karl Weierstrass (por su alumno Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), y Richard Dedekind. Meray hab??a tomado en 1869 el mismo punto de partida, Heine, pero la teor??a se denomina generalmente el a??o 1872. m??todo de Weierstrass ha sido completamente establecido por Salvatore Pincherle en 1880, y Dedekind ha recibido prominencia adicional a trav??s de la obra del autor m??s tarde (1888) y la reciente aprobaci??n por parte de Paul Curtidur??a (1894). Weierstrass, Cantor y Heine basan sus teor??as en las series infinitas, mientras que Dedekind funda su en la idea de un cortar (schnitt) en el sistema de los n??meros reales , separando todos los n??meros racionales en dos grupos que tienen ciertas propiedades caracter??sticas. El sujeto ha recibido contribuciones posteriores a manos de Weierstrass, Kronecker (Crelle, 101), y Meray.

Fracciones continuas, estrechamente relacionados con los n??meros irracionales (y debido a Cataldi, 1613), recibieron atenci??n por parte de Euler , y en la apertura del siglo XIX trajeron a la prominencia a trav??s de los escritos de Lagrange . Dirichlet tambi??n a??adido a la teor??a general, al igual que numerosos contribuyentes a las aplicaciones de la asignatura.

Lambert demostr?? (1761) que π no puede ser racional, y que e ⁿ es irracional si n es racional (a menos que n = 0). Mientras que la prueba de Lambert se dice a menudo para ser incompleta, evaluaciones modernos soportan como satisfactoria, y de hecho para su tiempo inusualmente riguroso. Legendre (1794), despu??s de la introducci??n de la Funci??n de Bessel-Clifford, proporcion?? una prueba para demostrar que π ² es irracional, de donde se sigue inmediatamente que π es irracional tambi??n. La existencia de los n??meros trascendentes fue establecida por primera vez por Liouville (1844, 1851). M??s tarde, Georg Cantor (1873) demostr?? su existencia por un m??todo diferente, que mostr?? que cada intervalo en los reales contiene n??meros trascendentes. Charles Hermite (1873) primera demostrado trascendental, y Ferdinand von Lindemann (1882), a partir de las conclusiones de Hermite, mostr?? el mismo para π. La demostraci??n de Lindemann se simplifica mucho por Weierstrass (1885), a??n m??s por David Hilbert (1893), y finalmente se hizo elemental Adolf Hurwitz y Paul Albert Gordan.

Ejemplo pruebas

La ra??z cuadrada de 2

La irracionalidad de la ra??z cuadrada de 2 podr?? probarse por suponiendo que es racional y deducir una contradicci??n, llamada un argumento por reducci??n al absurdo. El siguiente argumento apela dos veces al hecho de que el cuadrado de un entero impar es siempre impar.

Si √ 2 es racional que tiene la forma m / n para los n??meros enteros m, n no ambos incluso. Entonces m ?? = 2 n ?? donde m es par, decir m = 2 p. As?? 4 p ?? = 2 n ?? as?? que 2 p ?? = n ?? donde n es tambi??n incluso, una contradicci??n.

Otra prueba

La siguiente argumento reducci??n al absurdo es menos conocido. Utiliza la informaci??n adicional √2> 1.

1. Supongamos que √2 es un n??mero racional. Esto significar??a que existen enteros m y n con n ≠ 0 tal que m / n = √2.
2. Entonces √2 tambi??n puede ser escrito como una fracci??n irreducible m / n con n??meros enteros positivos, porque √2> 0.
3. Entonces 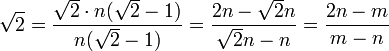, Porque .
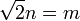4. Desde √2> 1, se deduce que m> n, que a su vez implica que m> 2 n - m.
5. As?? la fracci??n m / n para √2, que de acuerdo con (2) ya est?? en su m??nima expresi??n, es representado por (3) en t??rminos estrictamente inferiores. Esta es una contradicci??n, por lo que la hip??tesis de que √2 es racional debe ser falsa.

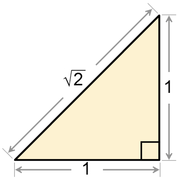
Del mismo modo, asumir un tri??ngulo rect??ngulo is??sceles cuya hipotenusa pierna y tienen longitudes respectivas nym enteros. Por el teorema de Pit??goras , la relaci??n m / n es igual a √2. Es posible construir por un cl??sico comp??s y una regla de construcci??n de un tri??ngulo rect??ngulo is??sceles peque??os cuya pierna y hipotenusa tienen longitudes respectivas m - n y 2 n - m. Esa construcci??n demuestra la irracionalidad de √2 por el tipo de m??todo que se emple?? por los antiguos ge??metras griegos.

La ra??z cuadrada de 10 y m??s all??

Si √ 10 es racional, digamos m / n, entonces m ² = 10 n ^2. Sin embargo, en notaci??n decimal, cada plaza termina en un n??mero par de ceros. Entonces m ² y 10 n ² en decimal debe terminar en respectivamente un n??mero par e impar de ceros, una contradicci??n.

M??s en general, en cualquier r radix que no es en s?? mismo un cuadrado, cada cuadrado termina en incluso un n??mero de ceros, de donde √ 10 _r en radix r es irracional, es decir, √ r es irracional. De ello se desprende que los ??nicos enteros con ra??ces cuadradas racionales son cuadrados. Como ejemplo de ello, 2 no es un cuadrado, y 2 en binario es 10 _2. (Nota de la convenci??n de sub??ndices n??meros no decimales con su ra??z, para evitar ambig??edades. Como parte de ese convenio se entienden los sub??ndices de estar en decimal, no siendo sub??ndice s?? mismos.)

Para ir a??n m??s lejos, podemos considerar m ^k = r ?? n ^k para cualquier enteros r y k. Si r ≠ u ^K para cualquier n??mero entero u, entonces R tiene al menos un factor primo p elevado a un exponente que no es divisible por k. Como todos los exponentes en la factorizaci??n prima de m ^k son divisible por k, para la ecuaci??n de celebrar, la descomposici??n en factores primos de n ^k debe contener p elevado a una potencia que tambi??n no es divisible por k. Pero esto es claramente imposible. Por lo tanto, para cualquier enteros r y k, ^k √ r es irracional si r ≠ u ^K para cualquier n??mero entero u. Este resultado tambi??n se deduce del hecho de que la crianza de un n??mero racional no integral a una potencia entera nunca puede ser igual a un n??mero entero, adem??s de 1.

La proporci??n ??urea

Cuando un segmento de l??nea se divide en dos subsegmentos disjuntos de una manera tal que la proporci??n de la totalidad de la parte m??s larga es igual a la relaci??n de la parte m??s larga de la parte m??s corta, a continuaci??n, que la relaci??n es la proporci??n ??urea , igual a

Supongamos que es un n??mero racional n / m en su m??nima expresi??n. Tome n a ser la longitud del conjunto y m la longitud de la parte m??s larga. Entonces n> m, y la longitud de la parte m??s corta es n - m. Entonces tenemos

Sin embargo, esto pone una fracci??n ya en su m??nima expresi??n en t??rminos inferiores -a contradicci??n. Por lo tanto, la hip??tesis inicial, que la proporci??n de oro es racional, es falsa.

Logaritmos

Tal vez los n??meros m??s f??cilmente demostraron ser irracional son ciertos logaritmos . Aqu?? est?? una prueba por reducci??n al absurdo que log ₂ 3 es irracional:

• Sup??ngase log ₂ 3 es racional. Para algunos enteros m y n positivos, tenemos log ₂ 3 = m / n.
• De ello se deduce que 2 ^{m / n} = 3.
• Levante cada lado a la potencia n, encontrar 2 ^m = 3 ^n.
• Pero 2 a cualquier potencia entero mayor que 0 es a??n (porque al menos uno de sus factores primos es 2) y 3 a cualquier potencia entero mayor que 0 es impar (porque ninguno de sus factores primos es 2), por lo que la suposici??n original es falsa.

Casos como log ₁₀ 2 pueden ser tratados de manera similar.

Irracionales trascendentes y algebraicos

Casi todos los n??meros irracionales son trascendentales y todo n??meros trascendentes son irracionales: el art??culo sobre los n??meros trascendentes enumera varios ejemplos e ^ry π ^r son irracionales si r ≠ 0 es racional; e ^π tambi??n es irracional..

Otra forma de construir los n??meros irracionales es tan irracional n??meros algebraicos, es decir, como ceros de polinomios con coeficientes enteros: comienzan con una ecuaci??n polin??mica

p (x) = a _n x ⁿ + a _n x ⁿ _-1 ^-1 + ... + a ₁ x + a = ₀ 0

donde los coeficientes a _i son n??meros enteros. Supongamos que usted sabe que existe alg??n n??mero real x con p (x) = 0 (por ejemplo, si n es impar y una _n no es cero, entonces, debido a la teorema del valor intermedio). Las ??nicas posibles ra??ces racionales de esta ecuaci??n polin??mica son de la forma r / s donde r es un divisor de un ₀ y s es un divisor de _n; s??lo hay un n??mero finito de tales candidatos que todos pueden cheque con la mano. Si ninguno de ellos es una ra??z de p, entonces x debe ser irracional. Por ejemplo, esta t??cnica se puede utilizar para demostrar que x = (2 ^1/2 + 1) ^1/3 es irracional: tenemos (x ³ - 1) ² = 2 y por lo tanto x ⁶ - 2 x ³ - 1 = 0 y este ??ltimo polinomio no tiene ning??n ra??ces racionales (los ??nicos candidatos para comprobar son ?? 1).

Debido a que los n??meros algebraicos forman una campo, muchos n??meros irracionales se puede construir mediante la combinaci??n de n??meros trascendentes y algebraicos. Por ejemplo 3π + 2, π + √ 2 y e √ 3 son irracionales (e incluso trascendental).

Expansiones decimales

La expansi??n decimal de un n??mero irracional nunca se repite o termina, a diferencia de un n??mero racional.

Para mostrar esto, supongamos que dividimos enteros n por m (donde m es distinto de cero). Cuando divisi??n larga se aplica a la divisi??n de n por m, solamente m restos son posibles. Si 0 aparece como un resto, la expansi??n decimal termina. Si 0 nunca ocurre, entonces el algoritmo se puede ejecutar como m??ximo m - 1 pasos sin utilizar ning??n resto m??s de una vez. Despu??s de eso, un resto debe repetirse, y luego las repeticiones expansi??n decimal!

Por el contrario, supongamos que estamos ante una decimal peri??dico, podemos demostrar que es una fracci??n de dos n??meros enteros. Por ejemplo:

Aqu?? la longitud de la repitend es 3. Se multiplica por 10 ^3:

Tenga en cuenta que ya hemos multiplicado por 10 elevado a la potencia de la longitud de la parte que se repite, cambiamos los d??gitos a la izquierda del punto decimal exactamente eso muchas posiciones. Por lo tanto, el extremo de cola de 1000 A coincide con el final de la cola de A exactamente. Aqu??, tanto 1.000 A y A han repitiendo 162 al final.

Por lo tanto, cuando se resta A de ambos lados, la parte final de 1000 A cancela fuera del extremo de la cola de A:

Entonces

que es un cociente de n??meros enteros y por lo tanto un n??mero racional.

Preguntas abiertas

No se sabe si π + e o π - e es irracional o no. De hecho, no hay ning??n par de n??meros enteros m y n no nulos para los que se sabe si m π + ne es irracional o no. Adem??s, no se sabe si el conjunto {π, e} es algebraicamente independiente sobre Q.

No se sabe si ^e 2, π ^e, π ^√2, Constante del catal??n, o el Euler-Mascheroni gamma γ constantes son irracionales.

El conjunto de todos los irracionales

Desde forman los reales una la multitud innumerable de los cuales los racionales son un subconjunto numerable, el conjunto complementario de los irracionales es incontable.

Bajo el habitual ( Euclidiana) funci??n de distancia d (x, y) = | x - y |, los n??meros reales son una espacio m??trico y por lo tanto tambi??n una espacio topol??gico. La restricci??n de la funci??n de distancia euclidiana da los irracionales la estructura de un espacio m??trico. Desde el subespacio de los irracionales no est?? cerrado, la m??trica inducida no es completa. Sin embargo, al ser una Conjunto G-delta - es decir, una intersecci??n numerable de subconjuntos abiertos - en un espacio m??trico completo, el espacio de los irracionales es topol??gicamente completa: es decir, no es un indicador de las irracionales que inducen la misma topolog??a como la restricci??n de la m??trica euclidiana, pero con respecto a la cual los irracionales son completa. Uno puede ver esto sin saber el hecho antes mencionado acerca de los conjuntos G-delta: la continua expansi??n fracci??n de un n??mero irracional define un homeomorfismo del espacio de los irracionales para el espacio de todas las secuencias de n??meros enteros positivos, que se ve f??cilmente que ser completamente metrizable.

Adem??s, el conjunto de todos los irracionales es un espacio m??trico desconectado.