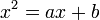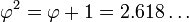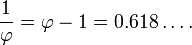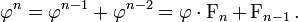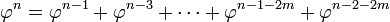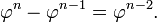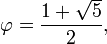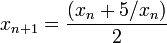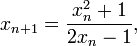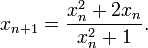Proporción áurea
Antecedentes
SOS Children han producido una selección de artículos de wikipedia para las escuelas desde el año 2005. El patrocinio infantil ayuda a los niños uno por uno http://www.sponsor-a-child.org.uk/ .


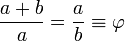 .
. En las matemáticas y las artes , dos cantidades están en la proporción áurea si el relación de la suma de las cantidades a la cantidad más grande es igual a la relación de la cantidad más grande a la más pequeña. La figura de la derecha muestra la relación geométrica. Expresado algebraicamente:
donde la letra griega phi ( 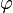 ) Representa la proporción áurea. Su valor es:
) Representa la proporción áurea. Su valor es:
El coeficiente de oro también se conoce como la sección áurea (latín: aurea secció) o justo medio. Otros nombres incluyen extrema y media razón, sección media, proporción divina, sección divina (latín: divina secció), proporción áurea, corte de oro, y el número de oro.
Muchos siglo 20 artistas y arquitectos han proporciónado sus trabajos para aproximar el coeficiente-especial de oro en forma de la rectángulo de oro, en el que la relación del lado más largo al más corto es la relación de oro creer que esta proporción sea estéticamente agradable (véase Aplicaciones y observaciones a continuación). matemáticos desde Euclides han estudiado las propiedades de la proporción áurea, incluyendo su aparición en las dimensiones de una pentágono regular y en un rectángulo de oro, que se puede cortar en un cuadrado y un rectángulo más pequeño con la misma relación de aspecto. El coeficiente de oro también se ha utilizado para analizar las proporciones de los objetos naturales así como sistemas hechos por el hombre tales como los mercados financieros, en algunos casos basados en ataques dudosos a los datos.
Cálculo
| |
| Binario | 1.1001111000110111011 ... |
| Decimal | 1,6180339887498948482 ... |
| Hexadecimal | 1.9E3779B97F4A7C15F39 ... |
| Fracción continua | 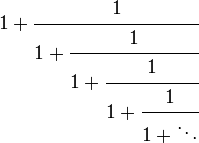 |
| Forma algebraica | 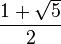 |
| Series infinitas | 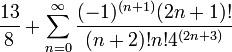 |
Dos cantidades a y b se dice que están en la proporción de oro φ si:
Un método para encontrar el valor de φ es comenzar con la fracción de la izquierda. A través de la simplificación de la fracción y sustituyendo en b / a = 1 / φ,
se muestra que
Multiplicando por φ da
que puede ser reorganizado para
Utilizando la fórmula cuadrática , se obtienen dos soluciones:
y
Debido al hecho de que φ es la relación entre la longitud y la anchura de un rectángulo, que no son cero, la solución positiva debe ser elegido:
Historia


La proporción de oro ha fascinado a los intelectuales occidentales de intereses diversos, por lo menos 2.400 años. De acuerdo a Mario Livio:
Algunas de las mentes más grandes matemáticos de todas las edades, desde Pitágoras y Euclides en la antigua Grecia , a través del matemático italiano medieval Leonardo de Pisa y el astrónomo renacentista Johannes Kepler , que hoy en día figuras científicas como Oxford físico Roger Penrose, han pasado horas interminables sobre esta sencilla relación y sus propiedades. Pero la fascinación por el cociente de oro no se limita sólo a los matemáticos. Los biólogos, artistas, músicos, historiadores, arquitectos, psicólogos, e incluso místicos han reflexionado y debatido sobre la base de su ubicuidad y apelación. De hecho, es probablemente justo decir que la Proporción Áurea ha inspirado a los pensadores de todas las disciplinas como ningún otro número en la historia de las matemáticas.
Griego antiguo matemáticos estudian primero lo que ahora llamamos la proporción áurea, debido a su frecuente aparición en la geometría . La división de una línea en "extrema y media razón" (la sección de oro) es importante en la geometría de ordinario pentagramas y pentágonos. El descubrimiento griegos generalmente atribuido de este concepto a Pitágoras o su seguidores. El pentagrama regular, que tiene un pentágono regular inscrito dentro de ella, era símbolo de los pitagóricos.
Euclides 's Elementos ( griego : Στοιχεῖα) proporciona la definición escrita primero conocido de lo que ahora se llama la proporción de oro: "Se dice que una línea recta que ha sido cortada en extrema y media razón cuando, como toda la línea es al segmento mayor , por lo que es la mayor a la menor ". Euclides explica una construcción para el corte (corte) una línea "en relación extrema y media", es decir, la proporción áurea. A lo largo de los Elementos, varias proposiciones ( teoremas en la terminología moderna) y sus pruebas emplean la proporción áurea. Algunas de estas propuestas muestran que la proporción de oro es un número irracional .
El nombre de "extrema y media razón" era el término principal usado desde el siglo tercero hasta el siglo 18o.
La historia moderna de la proporción áurea se inicia con Luca Pacioli de La divina proporción de 1509, que capturó la imaginación de los artistas, arquitectos, científicos y místicos con las propiedades, matemática y de otra manera, de la proporción áurea.
La primera aproximación conocida de la (inverso) proporción de oro por una fracción decimal , se indica como "aproximadamente 0,6180340", fue escrito en 1597 por Michael Maestlin de la Universidad de Tübingen, en una carta a su antiguo estudiante Johannes Kepler .
Desde el siglo 20 , la proporción de oro ha sido representado por la letra griega Φ o φ ( phi, después Fidias, escultor que se dice que ha empleado es) o menos comúnmente por τ ( tau, la primera letra del griego antiguo corte de raíz τομή intencionado).
Cronología
Línea de tiempo de acuerdo con Priya Hemenway:
- Fidias (490-430 aC) hizo las Partenón estatuas que parecen encarnar la proporción áurea.
- Platón (427-347 aC), en su Timeo, describe cinco posibles sólidos regulares (los sólidos platónicos : el tetraedro , cubo , octaedro , dodecaedro, y icosaedro), algunos de los cuales están relacionados con la proporción áurea.
- Euclides (.. c 325-c 265 aC), en sus elementos , dio la primera definición grabada de la proporción áurea, que él llamó, según la traducción en Inglés, "extrema y media razón" (griego: ἄκρος καὶ μέσος λόγος).
- Fibonacci (1170-1250) menciona la serie numérica ahora lleva su nombre en su Líber Abad; la relación de elementos secuenciales de la secuencia de Fibonacci se aproxima a la relación de asintóticamente de oro.
- Luca Pacioli (1445-1517) define la proporción de oro como la "divina proporción" en su divina proporción.
- Michael Maestlin (1550-1631) publica la primera aproximación conocida de la (inverso) proporción áurea como una fracción decimal .
- Johannes Kepler (1571-1630) demuestra que la proporción de oro es el límite de la relación de los números de Fibonacci consecutivos, y describe la proporción de oro como una "joya preciosa": "La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras , y la otra la división de una línea en relación extrema y media; el primero podemos comparar a una medida de oro, el segundo que puede nombrar a una joya preciosa ". Estos dos tesoros se combinan en el Triángulo de Kepler.
- De Charles Bonnet (1720-1793) señala que en la espiral filotaxis de plantas ir hacia la derecha y hacia la izquierda eran con frecuencia dos series sucesivas de Fibonacci.
- Martin Ohm (1792-1872) se cree que es el primero en utilizar el término goldener schnitt (sección de oro) para describir esta relación, en 1835.
- Édouard Lucas (1842-1891) da la secuencia numérica que ahora se conoce como la secuencia de Fibonacci su nombre actual.
- Marcos Barr (siglo 20) sugiere la letra griega phi (φ), la letra inicial del nombre del escultor griego Fidias, como símbolo de la proporción áurea.
- Roger Penrose (1931-) descubrió un patrón simétrico que utiliza la proporción de oro en el campo de teselaciones aperiódicas, lo que condujo a nuevos descubrimientos sobre cuasicristales.
Las solicitudes y observaciones
Estética
La divina proporción, una obra en tres volúmenes por Luca Pacioli, fue publicado en 1509. Pacioli, un Franciscano fraile, era conocido sobre todo como un matemático, sino que también fue entrenado y muy interesados en el arte. La divina proporción exploró las matemáticas de la proporción áurea. Aunque a menudo se dice que Pacioli abogó por la aplicación de la proporción áurea para producir, proporciones armoniosas agradables, Livio señala que la interpretación se ha remontado a un error en 1799, y que Pacioli realmente abogó por la Sistema de Vitruvio de proporciones racionales. Pacioli también vio significación religiosa católica en la relación, lo que llevó al título de su obra. Contiene ilustraciones de sólidos regulares por Leonardo da Vinci , viejo amigo de Pacioli y colaborador, La divina proporción fue una gran influencia sobre generaciones de artistas y arquitectos por igual.
Arquitectura

La fachada del Partenón, así como elementos de su fachada y en otros lugares se dice por algunos como circunscritos por rectángulos áureos. Otros eruditos negar que los griegos tenían ninguna asociación estética con proporción áurea. Por ejemplo, Midhat J. Gazale dice: "No fue sino hasta Euclides, sin embargo, que se estudiaron las propiedades matemáticas de la proporción áurea. En los Elementos (308 aC), el matemático griego simplemente considerado ese número como un número irracional interesante, en relación con las proporciones medias y extremas. Su presencia en pentágonos regulares y decágonos fue debidamente respetado, así como en el dodecaedro (una poliedro regular cuyas caras son doce pentágonos regulares). De hecho, es ejemplar que la gran Euclides, contrariamente a generaciones de místicos que siguieron, sobriamente trataría a ese número como lo que es, sin asociar a él con excepción de sus propiedades de hecho. "Y Keith Devlin dice: "Ciertamente, la afirmación tantas veces repetida de que el Partenón de Atenas se basa en la proporción áurea no está respaldada por medidas reales. De hecho, toda la historia de los griegos y proporción de oro parece ser sin fundamento. La única cosa que sabemos con certeza es que Euclides, en su famoso libro de texto Elementos, escrito alrededor del año 300 aC, mostró cómo calcular su valor ". Fuentes cercanas a la contemporáneos como Vitruvio discutir exclusivamente proporciones que se pueden expresar en números enteros, es decir, acorde a diferencia de proporciones irracionales.
A 2.004 análisis geométrico de la investigación anterior en la Gran Mezquita de Kairouan revela una aplicación coherente de la proporción áurea en todo el diseño, según Boussora y Mazouz. Encontraron proporciones cercanas a la proporción áurea en la proporción general de la planta y en el dimensionamiento del espacio de oración, el tribunal, y la minarete. Los autores señalan, sin embargo, que las zonas donde se encontraron proporciones cercanas a la proporción áurea no son parte de la construcción original, y la teoría de que estos elementos se han añadido en una reconstrucción.
El suizo arquitecto Le Corbusier, famoso por sus contribuciones a la moderno estilo internacional, centrado en su filosofía de diseño de sistemas de armonía y proporción. La fe de Le Corbusier en el orden matemático del universo estaba estrechamente ligada a la proporción áurea y la serie de Fibonacci, que ha calificado de "ritmos aparentes a la vista y claros en sus relaciones con los otros. Y estos ritmos están en la raíz misma de las actividades humanas. Resuenan en el hombre por una inevitabilidad orgánica, la misma inevitabilidad fina que hace que el trazado de la sección de oro por los niños, ancianos, los salvajes y los sabios ".
Le Corbusier utilizó explícitamente la proporción áurea en su Modulor sistema para la escala de proporción arquitectónico. Vio a este sistema como una continuación de la larga tradición de Vitruvio, de Leonardo da Vinci " Hombre de Vitruvio ", el trabajo de Leon Battista Alberti, y otros que utilizan las proporciones del cuerpo humano para mejorar la apariencia y función de la arquitectura . Además de la proporción áurea, Le Corbusier basa el sistema de mediciones humanos, los números de Fibonacci y la doble unidad. Él tomó la sugerencia de la proporción áurea en las proporciones humanas a un extremo: seccionó la altura de su modelo del cuerpo humano en el ombligo con las dos secciones en proporción áurea, luego subdividido esas secciones en proporción áurea en las rodillas y la garganta; él utilizó estas proporciones proporción de oro en el Sistema Modulor. De Le Corbusier 1927 Villa Stein en Garches ejemplifica la aplicación del sistema Modulor. El plan de la villa de planta rectangular, elevación, y la estructura interna de cerca aproximados rectángulos áureos.
Otro arquitecto suizo, Mario Botta, basa muchos de sus diseños en figuras geométricas. Varias casas privadas que diseñó en Suiza se componen de cuadrados y círculos, cubos y cilindros. En una casa que diseñó en Origlio, la proporción áurea es la proporción entre la sección central y las secciones laterales de la casa.
En un libro reciente, autor Jason Elliot especuló que la proporción de oro fue utilizado por los diseñadores de la Naqsh-e Jahan Square y la mezquita Lotfollah adyacente.
Pintura

El filósofo del siglo 16 Heinrich Agripa dibujó un hombre sobre un pentagrama dentro de un círculo, lo que implica una relación con la proporción áurea.
Leonardo da Vinci ilustraciones 's de poliedros en De proportione divina (En la divina proporción) y sus puntos de vista que algunas proporciones corporales muestran la proporción de oro han llevado a algunos estudiosos a especular que él incorporó la proporción áurea en sus pinturas. Pero la sugerencia de que su Mona Lisa , por ejemplo, emplea proporciones proporción de oro, no es apoyado por nada en los propios escritos de Leonardo. Del mismo modo, aunque el Hombre de Vitruvio menudo se muestra en relación con la proporción áurea, las proporciones de la figura en realidad no coincide con él, y el texto sólo menciona las relaciones de números enteros.
Salvador Dalí, influenciado por las obras de Matila Ghyka, utiliza explícitamente la proporción áurea en su obra maestra, La Última Cena. Las dimensiones de la lona son un rectángulo de oro. Un enorme dodecaedro, en perspectiva de modo que los bordes aparecen en proporción áurea el uno al otro, está suspendido por encima y detrás de Jesús y domina la composición.
Mondrian se ha dicho que han utilizado la sección de oro extensivamente en sus pinturas geométricas, aunque otros expertos (incluyendo crítico Yve-Alain Bois) han opuesto a esta tesis.
Un estudio estadístico sobre 565 obras de arte de diferentes grandes pintores, realizado en 1999, encontró que estos artistas no habían utilizado la proporción áurea en el tamaño de sus lienzos. El estudio concluyó que la proporción media de los dos lados de las pinturas estudiadas es de 1.34, con promedios de artistas individuales que van desde 1,04 (Goya) a 1,46 (Bellini). Por otro lado, Pablo Tosto aparece más de 350 obras de artistas de renombre, entre ellos más de 100 que tiene lienzos con rectángulo de oro y de la raíz 5-proporciones, y otros con proporciones como root-2, 3, 4 y 6.
Diseño del libro
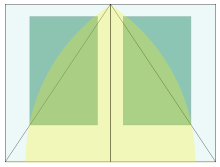
De acuerdo a Jan Tschichold,
Hubo un momento en que las desviaciones de la página verdaderamente hermosas proporciones 2: 3, 1: √3, y la sección áurea eran raros. Muchos libros producidos entre 1550 y 1770 muestran estas proporciones exactamente, a menos de medio milímetro.
Diseño Industrial
Algunas fuentes afirman que la proporción de oro se utiliza comúnmente en el diseño de todos los días, por ejemplo en la forma de postales, jugar a las cartas, carteles, televisores de pantalla ancha, fotografías y placas de interruptores de luz.
Música
Analiza Ernő Lendvai Obras de Béla Bartók como basado en dos sistemas opuestos, el de la proporción áurea y los escala acústica, aunque otros estudiosos de la música rechazan ese análisis. En Bartok Música para cuerdas, percusión y celesta la progresión xilófono se produce en los intervalos de 1: 2: 3: 5: 8: 5: 3: 2: 1. Compositor francés Erik Satie utilizó la proporción de oro en varias de sus piezas, incluyendo Sonneries de la Rose + Croix. El coeficiente de oro también es evidente en la organización de las secciones de la música de Debussy Reflets dans l'eau (Reflejos en el agua), a partir de imágenes (primera serie de 1905), en el que "la secuencia de teclas está marcada por los intervalos de 34, 21, 13 y 8, y el clímax principal se sienta en la posición de phi ".
El musicólogo Roy Howat ha observado que los límites formales de La Mer se corresponde exactamente con la sección áurea. Trezise encuentra la evidencia intrínseca "notable", pero advierte que no hay evidencia escrita o reportado sugiere que Debussy buscó conscientemente tales proporciones.
Pearl Drums posiciona las salidas de aire en sus modelos Masters prima basada en la proporción áurea. La compañía afirma que esta disposición mejora la respuesta de graves y ha solicitado una patentar en esta innovación.
Aunque Heinz Bohlen propuso la no-repetición de octava Escala de 833 centavos sobre la base de tonos combinados, las relaciones características de ajuste en función de la proporción áurea. Como intervalo musical la relación de 1,618 ... es ... 833,090 centavos de dólar (Play).
Naturaleza

Adolf Zeising, cuyo principal interés eran las matemáticas y la filosofía, encontró la proporción áurea expresado en la disposición de sucursales a lo largo de los tallos de las plantas y de las venas de las hojas. Extendió su investigación a los esqueletos de los animales y las ramificaciones de sus venas y nervios, a las proporciones de compuestos químicos y la geometría de los cristales, incluso con el uso de la proporción en actividades artísticas. En estos fenómenos que vio la proporción de oro que opera como una ley universal. En relación con su esquema para las proporciones del cuerpo humano basado oro-relación, Zeising escribió en 1854 de una ley universal "en el que se contiene el principio base de toda formativa lucha por la belleza y la integridad en los reinos de la naturaleza y el arte, y que impregna, como ideal supremo espiritual, todas las estructuras, formas y proporciones, ya sea cósmico o individual, orgánico o inorgánico, acústica u óptica; "que encuentra su plena realización, sin embargo, en la forma humana.
En 2010, la revista Science informó que la proporción de oro está presente a escala atómica en la resonancia magnética de giros en los cristales de niobato de cobalto.
Varios investigadores han propuesto conexiones entre la proporción áurea y genoma humano DNA .
Sin embargo, algunos han argumentado que muchas de las aparentes manifestaciones del oro significa en la naturaleza, especialmente en lo que se refiere a las dimensiones de los animales, de hecho son ficticios.
Optimización
La proporción áurea es clave para el búsqueda sección áurea.
Estudios de percepción
Los estudios realizados por los psicólogos, a partir de Fechner, se han ideado para probar la idea de que la proporción de oro juega un papel en la percepción humana de belleza. Mientras Fechner encontró una preferencia por relaciones rectángulo centrado en la proporción áurea, los intentos posteriores para probar cuidadosamente tal hipótesis han sido, en el mejor, no concluyentes.
Matemáticas
Relación de conjugado de oro
La raíz negativa de la ecuación cuadrática para φ (la "raíz conjugado") es
El valor absoluto de esta cantidad (≈ 0.618) corresponde a la relación de longitud tomada en orden inverso (longitud de segmento más corto sobre la longitud del segmento más largo, b / a), y se refiere a veces como la relación de conjugado de oro. Se denota aquí por la capital de la phi (Φ):
Alternativamente, Φ se puede expresar como
Esto ilustra la propiedad única de la proporción áurea entre los números positivos, que
o su inversa:
Esto significa 0.61803 ...: 1 = 1: 1,61803 ....
Pruebas cortas de la irracionalidad
Contradicción de una expresión en su mínima expresión

Recordemos que:
- el todo es la parte más larga, más la parte más corta;
- el conjunto es la parte más larga como la parte más larga es la parte más corta.
Si llamamos a toda la n y la parte más larga m, entonces la segunda declaración anterior se convierte en
- n es m como m es n - m,
o, algebraicamente
Decir que φ es medio racional que φ es una fracción n / m donde n y m son números enteros. Podemos tomar n / m para estar en su mínima expresión y nym ser positivo. Pero si n / m es en su mínima expresión, entonces la identidad marcada (*) arriba dice m / (n - m) es en términos aún más bajos. Eso es una contradicción que se desprende de la hipótesis de que φ es racional.
Derivación de la irracionalidad de √5
Otra prueba, tal vez corto conocido de la irracionalidad de la proporción áurea más comúnmente hace uso de la cierre de los números racionales bajo la suma y la multiplicación. Si 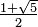 es racional, entonces
es racional, entonces 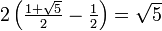 También es racional, que es una contradicción si ya se sabe que la raíz cuadrada de un no- plaza número natural es irracional.
También es racional, que es una contradicción si ya se sabe que la raíz cuadrada de un no- plaza número natural es irracional.
Las formas alternativas
La fórmula φ = 1 + 1 / φ se puede ampliar de forma recursiva para obtener una fracción continua de la proporción áurea:
y su recíproco:
La convergentes de estas fracciones continuas (1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ..., o 1/1, 1/2, 2/3, 3/5 , 5/8, 8/13, ...) son relaciones de los sucesivos números de Fibonacci .
La ecuación φ 2 = 1 + φ igualmente produce la continua raíz cuadrada , o irracional infinito, forma:
Una serie infinita se puede derivar de expresar phi:
También:
Estos corresponden al hecho de que la longitud de la diagonal de un pentágono regular es φ veces la longitud de su lado, y las relaciones similares en una pentagrama.
Geometría

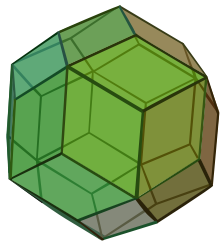
El número φ convierte con frecuencia en la geometría , en particular en las figuras con pentagonal simetría . La longitud de un habitual pentágono de diagonal es φ veces su lado. Los vértices de un habitual icosaedro son los de tres mutuamente ortogonal rectángulos áureos.
Allí no se sabe en general algoritmo para organizar un determinado número de nodos uniformemente sobre una esfera, por cualquiera de las diversas definiciones de la distribución uniforme (véase, por ejemplo, Problema Thomson). Sin embargo, unos resultados útiles de aproximación de la división de la esfera en bandas paralelas de la misma área y la colocación de un nodo en cada banda en longitudes separadas por una sección de oro del círculo, es decir, 360 ° / φ ≅ 222,5 °. Este método se utiliza para organizar los 1.500 espejos del estudiante participativo satélite Starshine-3.
División de un segmento de línea

El siguiente algoritmo produce una construcción geométrica que divide una segmento de línea en dos segmentos de línea donde la relación del tiempo para el segmento de línea más corto es el cociente de oro:
- Tener un segmento de línea AB, BC construir una perpendicular en el punto B, con BC mitad de la longitud de AB. Dibujar el hipotenusa AC.
- Dibuja un círculo con centro en C y radio de BC. Este círculo se cruza con la hipotenusa AC en el punto D.
- Dibuja un círculo con centro en A y radio AD. Este círculo se cruza con el segmento de línea AB original en el punto S. Point S divide el segmento AB original en segmentos de línea AS y SB con longitudes en la proporción áurea.
Triángulo de Oro, pentágono y pentagrama
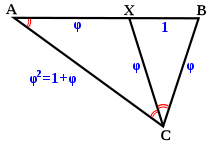
Triángulo de Oro
La triángulo de oro se puede caracterizar como un triángulo isósceles ABC con la propiedad de que bisectriz del ángulo C produce un nuevo triángulo CXB que es un triángulo similar a la original.
Si el ángulo de BCX = α, entonces XCA = α debido a la bisección, y CAB = α debido a los triángulos semejantes; ABC = 2α de la simetría isósceles original, y BXC = 2α por similitud. Los ángulos de un triángulo suman 180 °, por lo 5α = 180, dando α = 36 °. Así que los ángulos del triángulo de oro son, pues, 36 ° -72 ° -72 °. Los ángulos de los restantes triángulo isósceles obtusos AXC (a veces llamado el gnomon de oro) son 36 ° -36 ° -108 °.
Supongamos XB tiene longitud 1, y que llamamos longitud BC φ. Debido a la triángulos isósceles XC = XA y BC = XC, así que estos son también longitud φ. Longitud AC = AB, por lo tanto, es igual a φ + 1. Pero el triángulo ABC es similar al triángulo CXB, por lo AC / AC = BC / BX, y así AC es también igual a φ 2. Así φ 2 = φ + 1, lo que confirma que φ es de hecho la proporción áurea.
Del mismo modo, la relación entre el área de la más grande AXC triángulo a la CXB más pequeño es igual a φ, mientras que la razón inversa es φ - 1.
Pentágono
En un pentágono regular la relación entre un lado y una diagonal es 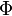 (Es decir, 1 / φ), mientras que intersecta la sección diagonales entre sí en la proporción áurea.
(Es decir, 1 / φ), mientras que intersecta la sección diagonales entre sí en la proporción áurea.
Construcción de Odom

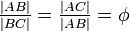
George Odom ha dado una construcción muy simple para φ que implica un triángulo equilátero: si un triángulo equilátero inscrito en un círculo y el segmento de recta que une los puntos medios de dos lados se produce para intersectar el círculo en cualquiera de los dos puntos, entonces estos tres puntos están en proporción áurea. Este resultado es una consecuencia directa de la intersección acordes teorema y se pueden usar para construir un pentágono regular, una construcción que atrajo la atención del geómetra canadiense señalado HSM Coxeter, que lo publicó en nombre de Odom como un diagrama en el American Mathematical Monthly acompañada por la palabra "¡He aquí!"
Pentagram
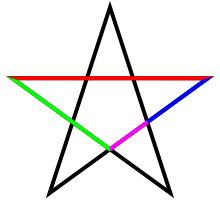
La proporción de oro juega un papel importante en la geometría de pentagramas. Cada intersección de bordes secciones otras aristas en la proporción áurea. Además, la relación de la longitud del segmento más corto para el segmento delimitado por los dos bordes de intersección (un lado del pentágono en el centro de la estrella de cinco puntas) es φ, como los cuatro colores ilustración muestra.
El pentagrama incluye diez triángulos isósceles : cinco aguda y cinco obtusos triángulos isósceles. En todos ellos, la relación del lado largo al lado más corto es φ. Los triángulos son agudos triángulos de oro. Los triángulos isósceles obtusos son gnomones oro.
El teorema de Ptolomeo

Las propiedades proporción de oro de un pentágono regular se puede confirmar mediante la aplicación de El teorema de Ptolomeo al cuadrilátero formado por la eliminación de uno de sus vértices. Si el borde y diagonales largo del cuadrilátero son b, y bordes cortos son una, entonces el teorema de Ptolomeo da b 2 = a + ab que los rendimientos de 2
Scalenity de triángulos
Considere un triángulo con lados de longitudes a, b, y c en orden decreciente. Definir el "scalenity" del triángulo ser la más pequeña de las dos relaciones A / B y B / C. El scalenity es siempre menor que φ y se puede hacer tan cerca como se desee para φ.
Lados del triángulo cuyos forman una progresión geométrica
Si las longitudes de los lados de un triángulo forma una progresión geométrica y están en la relación de 1: r: r 2, donde r es la relación común, entonces R debe estar en el intervalo φ-1 <r <φ, que es una consecuencia de la desigualdad triangular (la suma de cualquiera de los dos lados de un triángulo debe ser estrictamente mayor que la longitud del tercer lado). Si r = φ entonces los dos lados más cortos son 1 y φ pero su suma es φ 2, por lo tanto r <φ. Un cálculo similar muestra que r> φ-1. Un triángulo cuyos lados están en la relación de 1: √φ: φ es un triángulo rectángulo (porque 1 + φ φ = 2) conocido como Triángulo de Kepler.
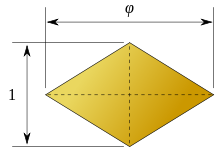
Oro triángulo, rombo, y triacontaedro rómbico
La rombo de oro es un rombo cuyas diagonales se encuentran en la proporción áurea. La triacontaedro rómbica es una politopo convexo que tiene una propiedad muy especial: todas sus caras son rombos de oro. En el rómbica triacontaedro la ángulo diedro entre dos rombos adyacente es 144 °, que es dos veces el ángulo de un isósceles triángulo de oro y cuatro veces su ángulo más agudo.
Relación con la secuencia de Fibonacci
La matemática de la proporción áurea y de la sucesión de Fibonacci están íntimamente interconectados. La secuencia de Fibonacci es la siguiente:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ....
La expresión de forma cerrada (conocido como La fórmula de Binet, a pesar de que ya era conocido por Abraham de Moivre) para la secuencia de Fibonacci implica la proporción áurea:

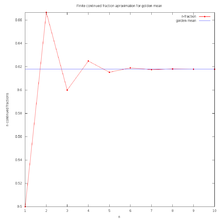
La proporción áurea es la límite de los coeficientes de los términos sucesivos de la secuencia de Fibonacci (o cualquier secuencia de Fibonacci similares), como se muestra originalmente por Kepler :
Por lo tanto, si un número Fibonacci se divide por su predecesor inmediato en la secuencia, el cociente se aproxima φ; por ejemplo, 987/610 ≈ 1,6180327868852. Estas aproximaciones son alternativamente menor y mayor que φ, y convergen en φ como el número de aumento de Fibonacci, y:
Más generalmente:
donde anteriormente, las relaciones de términos consecutivos de la sucesión de Fibonacci, es un caso en el que 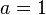 .
.
Por otra parte, las sucesivas potencias de φ obedecen la Fibonacci recurrencia:
Esta identidad permite que cualquier polinomio en φ se reduzca a una expresión lineal. Por ejemplo:
Sin embargo, esto no es una propiedad especial de φ, porque polinomios en cualquier solución de x a una ecuación de segundo grado se pueden reducir de una manera análoga, mediante la aplicación de:
para coeficientes dados un , b tales que x satisface la ecuación. Aún más en general, cualquier función racional (con coeficientes racionales) de la raíz de un irreducible n th-grado del polinomio sobre los números racionales se puede reducir a un polinomio de grado n - 1. Expresado en términos de la teoría de campo, si α es una raíz de un irreducible n th-grado del polinomio, entonces 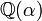 tiene grado n sobre
tiene grado n sobre 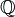 , con base
, con base 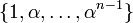 .
.
Simetrías
La proporción áurea y la proporción áurea inversa 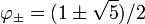 tienen un conjunto de simetrías que preservan y se interrelacionan ellos. Ambos son preservados por las transformaciones lineales fraccionarias
tienen un conjunto de simetrías que preservan y se interrelacionan ellos. Ambos son preservados por las transformaciones lineales fraccionarias 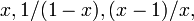 - este hecho corresponde a la identidad y la ecuación cuadrática definición. Además, que se intercambian por los tres mapas
- este hecho corresponde a la identidad y la ecuación cuadrática definición. Además, que se intercambian por los tres mapas 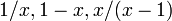 - que son recíprocos, simétrica respecto
- que son recíprocos, simétrica respecto 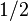 , y (proyectivamente) simétrica alrededor de 2.
, y (proyectivamente) simétrica alrededor de 2.
Más profundamente, estos mapas forman un subgrupo delgrupo modular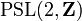 isomorfo algrupo simétrico en 3 letras,
isomorfo algrupo simétrico en 3 letras,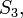 correspondiente alestabilizador del conjunto
correspondiente alestabilizador del conjunto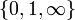 de 3 puntos estándar en lalínea proyectiva, y las simetrías corresponden al mapa cociente
de 3 puntos estándar en lalínea proyectiva, y las simetrías corresponden al mapa cociente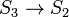 - el subgrupo
- el subgrupo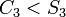 que consiste en los 3-ciclos y la identidad
que consiste en los 3-ciclos y la identidad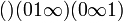 fija los dos números, mientras que los 2 ciclos intercambian estos, realizando así el mapa.
fija los dos números, mientras que los 2 ciclos intercambian estos, realizando así el mapa.
Otras propiedades
La proporción áurea tiene la expresión más simple (y la convergencia más lenta) como una expansión continua fracción de cualquier número irracional (ver formas alternativas anteriores). Es, por ello, uno de los peores casos de aproximación teorema de Lagrange y es un caso extremal de la desigualdad de Hurwitz para aproximaciones diofánticas. Tal vez por eso los ángulos cerca de la proporción áurea menudo aparece en filotaxis (el crecimiento de las plantas).
El polinomio de segundo grado la definición y la relación conjugada conducen a valores decimales que tienen su parte fraccionaria en común con φ:
La secuencia de los poderes de φ contiene estos valores 0.618 ..., 1,0, 1,618 ..., 2.618 ...; más en general, cualquier potencia de φ es igual a la suma de las dos potencias inmediatamente anteriores:
Como resultado, se puede descomponer fácilmente cualquier poder de φ en un múltiplo de φ y una constante. El múltiple y la constante son siempre los números de Fibonacci adyacentes. Esto nos lleva a otra propiedad de los poderes positivos de φ:
Si 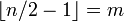 , Luego:
, Luego:
Cuando se utiliza la proporción áurea como la base de unsistema de numeración(verbase de la relación de oro, a veces apodadophinaryoφ-nario), todo entero tiene una representación de terminación, a pesar de φ ser irracional, pero cada fracción tiene una representación no terminar.
La proporción áurea es unaunidad fundamental delcampo de número algebraico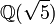 y es unnúmero Pisot-Vijayaraghavan. En el campo
y es unnúmero Pisot-Vijayaraghavan. En el campo 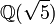 tenemos
tenemos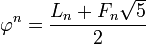 , Donde
, Donde 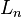 es el
es el 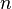 -ésimonúmero Lucas.
-ésimonúmero Lucas.
El coeficiente de oro también aparece enla geometría hiperbólica, como la distancia máxima desde un punto en un lado de untriángulo ideal para la más cerca de los otros dos lados: esta distancia, la longitud del lado deltriángulo equilátero formado por los puntos de tangencia de una círculo inscrito en el triángulo ideal es 4 ln φ.
Expansión decimal
Expansión decimal del número áureo puede calcularse directamente a partir de la expresión
con √5 ≈ 2.2360679774997896964. La raíz cuadrada de 5 se puede calcular con elmétodo de Babilonia, a partir de una estimación inicial comoxφ = 2 yla iteración
paran= 1, 2, 3, ..., hasta que la diferencia entrexnyx n-1se convierte en cero, hasta el número deseado de dígitos.
El algoritmo de Babilonia para √5 es equivalente al método de Newton para resolver la ecuación x 2 - 5 = 0. En su forma más general, el método de Newton se puede aplicar directamente a cualquier ecuación algebraica, incluyendo la ecuación x 2 - x - 1 = 0 que define la proporción áurea. Esto le da una iteración que converge a la propia razón áurea,
para una estimación inicial apropiadoxφ tales comox= φ 1. Un método ligeramente más rápido es volver a escribir la ecuación comox- 1 - 1 /x= 0, en cuyo caso la iteración de Newton se convierte
Estas iteraciones todos convergen cuadrática; es decir, cada paso aproximadamente duplica el número de dígitos correctos. La proporción áurea es, por tanto, relativamente fácil de calcular con precisión arbitraria. El tiempo necesario para calcular n dígitos de la proporción áurea es proporcional al tiempo necesario para dividir dos n números de dígitos. Esto es considerablemente más rápido que los algoritmos conocidos para los números trascendentales π y e .
Una alternativa fácil programada utilizando sólo la aritmética de enteros es calcular dos grandes números de Fibonacci consecutivos y dividirlos. La relación de los números de Fibonacci F 25001 y F 25000 , cada uno más de 5.000 dígitos, los rendimientos de más de 10.000 dígitos significativos de la proporción áurea.
El número áureo φ se ha calculado con una precisión de varios millones de dígitos decimales (secuencia A001622 en OEIS ). Alexis Irlande realiza cálculos y la verificación de los primeros 17 mil millones dígitos.
Pirámides

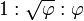 y
y 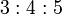 y
y 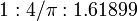 son de particular interés en relación con las pirámides de Egipto.
son de particular interés en relación con las pirámides de Egipto. Ambas pirámides de Egipto y aquellos regulares matemáticospirámides cuadradas que se parecen a ellos pueden ser analizados con respecto a la proporción de oro y otros ratios.
Pirámides matemáticas y triángulos
Una pirámide en la que la apotema (altura inclinada a lo largo de la bisectriz de un rostro) es igual a φ veces el semi-base (la mitad de la anchura de la base) que a veces se llama una pirámide dorada . El triángulo isósceles que es la cara de una pirámide como se puede construir a partir de las dos mitades de un rectángulo de oro en diagonal dividir (de tamaño semi-base por apotema), que unen los bordes de longitud media para hacer la apotema. La altura de esta pirámide es 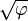 veces el semi-base (es decir, la pendiente de la cara es
veces el semi-base (es decir, la pendiente de la cara es 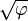 ); el cuadrado de la altura es igual al área de una cara, los tiempos de φ el cuadrado de la semi-base.
); el cuadrado de la altura es igual al área de una cara, los tiempos de φ el cuadrado de la semi-base.
El medialtriángulo rectángulo de esta pirámide "de oro" (ver diagrama), con lados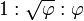 es interesante en sí mismo, lo que demuestra a través delteorema de Pitágorasla relación
es interesante en sí mismo, lo que demuestra a través delteorema de Pitágorasla relación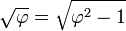 o
o 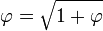 . Este " Kepler triángulo "es la única proporción triángulo rectángulo con longitudes de borde enprogresión geométrica, así como el 3-4-5 triángulo es la única proporción triángulo rectángulo con longitudes de arista enprogresión aritmética. El ángulo con la tangente
. Este " Kepler triángulo "es la única proporción triángulo rectángulo con longitudes de borde enprogresión geométrica, así como el 3-4-5 triángulo es la única proporción triángulo rectángulo con longitudes de arista enprogresión aritmética. El ángulo con la tangente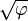 corresponde al ángulo que el lado de la pirámide hace con respecto al suelo, 51.827 ... grados (51 ° 49 ' 38 ").
corresponde al ángulo que el lado de la pirámide hace con respecto al suelo, 51.827 ... grados (51 ° 49 ' 38 ").
Una forma de pirámide casi similar, pero con proporciones racionales, se describe en el papiro matemático de Rhind (la fuente de una gran parte del conocimiento moderno de la antigua matemáticas egipcio), basado en el 3: 4: 5 triángulo; la pendiente cara correspondiente al ángulo tangente con 4/3 es 53.13 grados (53 grados y 8 minutos). La altura inclinada o apotema es 5/3 o 1,666 ... veces el semi-base. El papiro Rhind tiene otro problema pirámide, así, de nuevo con pendiente racional (expresado como carrera en ascenso). Matemáticas egipcias no incluían la noción de los números irracionales, y la pendiente inversa racional (run / subida, multiplicada por un factor de 7 para convertir a sus unidades convencionales de palmas por codo) se utilizó en la construcción de las pirámides.
Otra pirámide matemática con proporciones casi idénticas a la "dorada" uno es el que tiene el perímetro igual a 2π veces la altura, o h: b = 4: π. Este triángulo tiene un ángulo de la cara de 51.854 ° (51 ° 51 '), muy cerca de la ° 51.827 de la Triángulo de Kepler. relación Esta pirámide corresponde a la relación de coincidencia 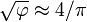 .
.
Son conocidas pirámides de Egipto muy cerca en proporción a estas pirámides matemáticas.
Piramides de Egipto
En la mitad del siglo XIX, Röber estudió varias pirámides de Egipto, incluyendo Kefrén, Micerinos y algunas de las de Giza, Saqqara y Abusir grupos, y fue interpretado como diciendo que la mitad de la base del lado de la pirámide es la media mitad del lado , formando lo que otros autores identificados como el triángulo de Kepler; muchas otras teorías matemáticas de la forma de las pirámides también han sido exploradas.
Una pirámide egipcia es muy cerca de una "pirámide de oro", la Gran Pirámide de Giza (también conocido como la Pirámide de Keops o Khufu). Su pendiente de 51 ° 52 'está muy cerca de la "dorada" pirámide de inclinación de 51 ° 50' y la pirámide inclinación a base de π de 51 ° 51 '; otras pirámides de Giza (Kefrén, 52 ° 20 ', y Micerino, 50 ° 47') también están muy cerca. Ya sea que la relación con la proporción áurea en estas pirámides es por diseño o por accidente permanece abierta a la especulación. Varias otras pirámides egipcias están muy cerca de lo racional 3: 4: 5 forma.
Echando más leña a la controversia sobre la autoría de arquitectura de la Gran Pirámide,Eric Temple Bell, matemático e historiador, afirmó en 1950 que las matemáticas egipcias no han apoyado la capacidad de calcular la altura inclinada de las pirámides, o la relación con la altura, excepto en el caso del 3: 4: 5 pirámide, ya que el 3: 4: 5 triángulo era el único triángulo rectángulo conocido por los egipcios y que no conocía el teorema de Pitágoras, ni ninguna manera de razonar sobre los irracionales como π o φ .
Michael Rice afirma que las autoridades principales en la historia de la arquitectura egipcia han argumentado que los egipcios estaban bien familiarizados con la proporción áurea y que es parte de la matemática de las Pirámides, citando Giedon (1957). Los historiadores de la ciencia siempre han debatido si los egipcios tenían tal conocimiento o no, más bien afirmando que su aparición en un edificio egipcio es el resultado de la casualidad.
En 1859, el Pyramidologist John Taylor afirmó que, en la Gran Pirámide de Giza , la proporción áurea está representada por la relación de la longitud de la cara (la altura de pendiente), inclinada en un ángulo θ a la tierra, a la mitad de la longitud del lado de la base cuadrada, equivalente a la secante del ángulo θ. Los dos longitudes superiores estaban a punto 186,4 y 115,2 metros, respectivamente. La relación de estas longitudes es la proporción áurea, precisa a más dígitos que cualquiera de las mediciones originales. Del mismo modo, Howard Vyse, de acuerdo con Matila Ghyka, informaron la gran altura pirámide 148,2 m, y medio-base 116.4 m, obteniéndose 1,6189 para la relación de altura inclinada a medio-base, de nuevo más precisa que la variabilidad de los datos.
Observaciones en disputa
Ejemplos de observaciones en disputa de la proporción áurea se incluyen las siguientes:
- El historiador John Hombre establece que las páginas de la Biblia de Gutenberg se "basan en la forma de la sección de oro". Sin embargo, según las propias mediciones del hombre, la relación de altura y ancho era 1.45.
- Algunas proporciones específicas en los cuerpos de muchos animales (incluidos los humanos) y partes de las conchas de los moluscos y cefalópodos son a menudo afirmaban estar en la proporción áurea. Hay una gran variación en las medidas reales de estos elementos en individuos específicos, sin embargo, y la proporción en cuestión es a menudo significativamente diferente de la proporción áurea. La relación de los sucesivos huesos de las falanges de los dedos y el hueso metacarpiano se ha dicho para aproximar la proporción áurea. La Nautilus Shell, cuya construcción avanza en una espiral logarítmica, se cita a menudo, por lo general con la idea de que cualquier espiral logarítmica se relaciona con la proporción áurea, pero a veces con la afirmación de que cada nueva cámara es proporcionada por el cociente de oro con respecto a la anterior; Sin embargo, las mediciones de conchas nautilus no apoyan esta afirmación.
- Las proporciones de los diferentes componentes de la planta (número de hojas a las ramas, diámetros de las figuras geométricas dentro de las flores) a menudo son reclamados para mostrar la relación de proporción de oro en varias especies. En la práctica, hay variaciones significativas entre los individuos, las variaciones estacionales y variaciones de edad en estas especies. Mientras que la proporción de oro se puede encontrar en algunas proporciones en algunos individuos en momentos concretos en sus ciclos de vida, no hay ninguna relación coherente en sus proporciones.
- En la inversión, algunos practicantes de análisis técnico utilizan la proporción áurea para indicar el apoyo de un nivel de precios, o la resistencia a los aumentos de precios, de una población o de los productos básicos; después significativa de los precios cambia hacia arriba o abajo, los nuevos niveles de soporte y resistencia son supuestamente encontraron en o cerca de los precios relacionados con el precio de salida a través de la proporción áurea. El uso de la proporción áurea en la inversión también se relaciona con los patrones más complicados descritos por los números de Fibonacci (por ejemplo, principio de la onda de Elliott y de retroceso de Fibonacci). Sin embargo, otros analistas de mercado han publicado análisis que sugieren que estos porcentajes y los patrones no están respaldadas por los datos.
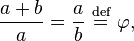
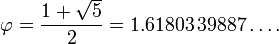
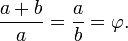
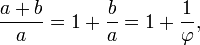
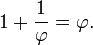
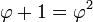
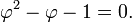
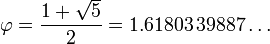
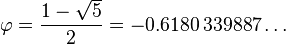
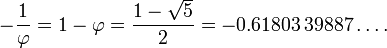
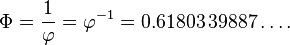
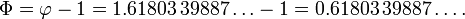
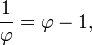
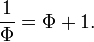
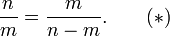
![\ Varphi = [1; 1, 1, 1, \ dots] = 1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ ddots}}}](../../images/2794/279449.png)
![\ Varphi ^ {- 1} = [0; 1, 1, 1, \ dots] = 0 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ ddots}}}](../../images/2794/279450.png)
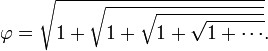
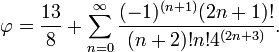
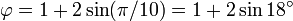
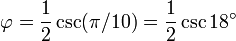
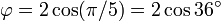
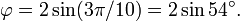
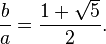
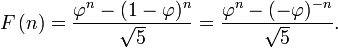
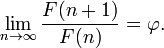
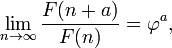
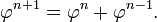
![\ Begin {align} 3 \ varphi ^ 3-5 \ phi ^ 2 + 4 y = 3 (\ phi ^ 2 + \ phi) - 5 \ phi ^ 2 + 4 \\ & = 3 [(\ varphi + 1) + \ phi] - 5 (\ varphi + 1) + 4 \\ & = \ varphi + 2 \ aprox 3.618. \ End {align}](../../images/2795/279500.png)