Teorema

Una imagen vale más que mil matemática palabras: el teorema de Pitágoras .

En la lógica matemática, un teorema es un tipo de objeto abstracto, uno señal de que es una fórmula de una lenguaje formal que puede derivarse de la reglas del sistema formal que se aplica a la lengua formal; otra señal de que es una declaración en lenguaje natural, que puede ser demostrado sobre la base de supuestos indicados explícitamente o previamente acordados.

En todos los ámbitos, una propiedad esencial de teoremas es que son derivables usando un conjunto fijo de reglas de inferencia y axiomas sin ninguna hipótesis adicional. Esto no es una cuestión de la semántica del lenguaje: la expresión que resulta de una derivación es una consecuencia sintáctica de todas las expresiones que lo preceden. En matemáticas , la derivación de un teorema se interpreta a menudo como una prueba de la verdad de la expresión resultante, pero diferente sistemas deductivos pueden producir otras interpretaciones, dependiendo de los significados de las reglas de derivación.

Las demostraciones de teoremas tienen dos componentes, que se llama hipótesis y la conclusiones. La demostración de un teorema matemático es un argumento lógico que demuestra que las conclusiones son una consecuencia necesaria de las hipótesis, en el sentido de que si las hipótesis son verdaderas entonces las conclusiones también deben ser verdaderas, sin ningún tipo de suposiciones adicionales. Por tanto, el concepto de un teorema es fundamentalmente deductivo, en contraste con la noción de un científico teoría, que es empírica.

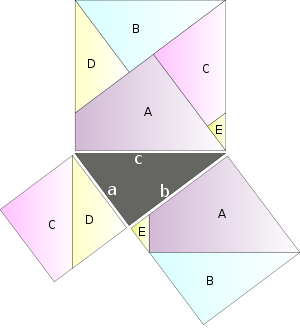
A pesar de que se pueden escribir en un completamente de forma simbólica, teoremas se expresa a menudo en un lenguaje natural como el Inglés. Lo mismo puede decirse de las pruebas, que se expresan a menudo como lógicamente organizada y clara redacción argumentos informales destinados a demostrar que una prueba simbólica formal puede ser construido. Tales argumentos son típicamente más fácil comprobar que las puramente simbólicos - de hecho, muchos matemáticos serían expresar una preferencia por una prueba de que no sólo demuestra la validez de un teorema, sino que también explica de alguna manera por qué es obviamente cierto. En algunos casos, una imagen por sí sola puede ser suficiente para demostrar un teorema.

Debido teoremas encuentran en el núcleo de las matemáticas, que también son fundamentales para su estética. Los teoremas son a menudo descrito como "trivial" o "difícil" o "profundo", o incluso "hermosa". Estos juicios subjetivos varían no sólo de persona a persona, pero también con el tiempo: por ejemplo, como una prueba de ello es simplificada o mejor entendido, un teorema que alguna vez fue difícil puede llegar a ser trivial. Por otro lado, un teorema profundo puede ser simplemente dijo, pero su prueba puede implicar conexiones sorprendentes y sutiles entre áreas dispares de las matemáticas. el último teorema de Fermat es un ejemplo particularmente bien conocido de tal teorema.

Nociones formales e informales

Lógicamente la mayoría de los teoremas son de la forma de una indicativo condicional:. si A, entonces B Tal teorema no dice que B es siempre cierto, sólo que B debe ser verdadera si A es verdad. En este caso A se llama hipótesis del teorema (tenga en cuenta que "hipótesis" aquí es algo muy diferente de un conjetura) y B la conclusión. El teorema "Si n es un número natural entonces n / 2 es un número natural "es un ejemplo típico en el que la hipótesis es que n es un número par natural y la conclusión es que n / 2 también es un número natural.

Con el fin de ser probada, un teorema debe ser expresable como una declaración precisa, formal. Sin embargo, teoremas se suelen expresar en lenguaje natural en vez de en una forma completamente simbólica, con la intención de que el lector será capaz de producir una declaración formal de la informal. Además, a menudo hay hipótesis que se entienden en el contexto, en lugar de explícitamente.

Es común en las matemáticas para elegir una serie de hipótesis que se asumen para ser verdad dentro de una teoría dada, y luego declaran que la teoría se compone de todos los teoremas comprobables utilizando esas hipótesis como hipótesis. En este caso las hipótesis que forman la base fundacional se denominan axiomas (o postulados) de la teoría. El campo de las matemáticas conocida como teoría de la prueba estudia sistemas axiomáticos formales y las pruebas que se pueden realizar dentro de ellos.

Un plano mapa con cinco colores de tal manera que no hay dos regiones con el mismo color se encuentran. En realidad, puede ser de color de esta manera con sólo cuatro colores. El teorema de los cuatro colores establece que tales colorantes son posibles para cualquier mapa planar, pero cada prueba conocido implica una búsqueda computacional que es demasiado largo para comprobar con la mano.

Algunos teoremas son "trivial", en el sentido de que se siguen de definiciones, axiomas y teoremas en otras maneras obvias y no contienen ideas sorprendentes. Algunos, por el contrario, pueden ser llamados "profundo": sus pruebas pueden ser largo y difícil, involucra áreas de las matemáticas superficialmente distinta de la declaración del propio teorema, o mostrar sorprendentes conexiones entre áreas dispares de las matemáticas. Un teorema puede ser simple de enunciar y sin embargo ser profundo. Un excelente ejemplo es el último teorema de Fermat , y hay muchos otros ejemplos de teoremas todavía profundas simples en la teoría de números y combinatoria , entre otras áreas.

Hay otros teoremas que caracterizan a una prueba, pero la prueba no pueden ser fácilmente escrito. Los ejemplos más destacados son el Teorema de los cuatro colores y el Conjetura de Kepler. Ambos de estos teoremas son sólo conocidos por ser verdadera reduciéndolas a una búsqueda computacional que luego se verificó mediante un programa informático. Inicialmente, muchos matemáticos no aceptaron esta forma de la prueba, pero se ha vuelto más ampliamente aceptadas en los últimos años. El matemático Doron Zeilberger ha ido tan lejos como para afirmar que estos son posiblemente los únicos resultados no triviales que los matemáticos siempre han demostrado. Muchos teoremas matemáticos pueden reducirse a cálculo más sencillo, incluyendo identidades polinómicas, identidades trigonométricas e identidades hipergeométrica.

Relación con la prueba

La noción de un teorema está profundamente entrelazado con el concepto de la prueba. De hecho, los teoremas son verdaderas precisamente en el sentido de que poseen pruebas. Por lo tanto, para establecer un enunciado matemático como un teorema, la existencia de una línea de razonamiento de los axiomas en el sistema (y otros teoremas ya establecidos) a la declaración dada debe ser demostrada.

Aunque la prueba es necesaria para producir un teorema, no se considera por lo general parte del teorema. Y a pesar de que más de una prueba puede ser conocido para un solo teorema, sólo se requiere una prueba para establecer la validez del teorema. El teorema de Pitágoras y la ley de reciprocidad cuadrática son candidatos al título del teorema con el mayor número de pruebas distintas.

Los teoremas de la lógica

Lógica , especialmente en el campo de la teoría de la prueba, considera teoremas como estados de cuenta (llamadas fórmulas o fórmulas bien formada) de una lenguaje formal. Un conjunto de reglas de deducción, también llamadas reglas de transformación o un gramática formal, debe ser proporcionada. Estas reglas de deducción dicen exactamente cuando una fórmula se puede derivar de un conjunto de premisas.

Los diferentes conjuntos de reglas de derivación dan lugar a diferentes interpretaciones de lo que significa para una expresión sea un teorema. Algunas reglas de derivación y lenguajes formales pretenden capturar el razonamiento matemático; los ejemplos más comunes utilizan la lógica de primer orden . Otros sistemas deductivos describen reescritura plazo, como las reglas de reducción de cálculo λ.

La definición de teoremas como elementos de un lenguaje formal permite obtener resultados en la teoría de la prueba de que estudian la estructura de las pruebas formales y la estructura de fórmulas demostrables. El resultado más famoso es Teorema de incompletitud de Gödel; mediante la representación de teoremas sobre la teoría de números básicos como expresiones en un lenguaje formal, y luego en representación de este lenguaje dentro de la teoría de números en sí, Gödel construyó ejemplos de declaraciones que no son ni demostrable ni refutable de axiomatizaciones de la teoría de números.

Relación con las teorías científicas

Los teoremas de las matemáticas y teorías de la ciencia son fundamentalmente diferentes en su epistemología. Una teoría científica no puede ser probada; su atributo clave es que es falsable, es decir, que hace predicciones sobre el mundo natural que son comprobables por experimentos. Cualquier desacuerdo entre la predicción y experimento demuestra la inexactitud de la teoría científica, o al menos limita su exactitud o dominio de validez. Teoremas matemáticos, por el contrario, son puramente declaraciones formales abstractos: la demostración de un teorema no puede implicar experimentos u otra evidencia empírica de la misma manera tal evidencia se utiliza para apoyar las teorías científicas.

La conjetura de Collatz: Una forma de ilustrar su complejidad es extender la iteración de los números naturales a los números complejos. El resultado es un fractal, que (de acuerdo con universalidad) es similar al conjunto de Mandelbrot .

Sin embargo, hay un cierto grado de empirismo y recopilación de datos involucrados en el descubrimiento de teoremas matemáticos. Mediante el establecimiento de un patrón, a veces con el uso de un ordenador potente, los matemáticos pueden tener una idea de lo que probar, y en algunos casos incluso un plan para saber cómo hacer de hacer la prueba. Por ejemplo, el Collatz conjetura ha sido verificado por valores de inicio hasta aproximadamente 2.88 × 10 ^18. El Hipótesis de Riemann se ha verificado durante los primeros 10 billones de ceros de la función zeta. Ninguna de estas declaraciones se considera que se ha demostrado.

Tales pruebas no constituye una prueba. Por ejemplo, el Mertens conjetura es una afirmación acerca de los números naturales que ahora se sabe que es falso, pero no contraejemplo explícito (es decir, un número natural n para el cual la función de Mertens M (n) es igual o superior a la raíz cuadrada de n) es conocida: todos los números menos de 10 ¹⁴ tienen la propiedad Mertens, y el número más pequeño que no tiene esta propiedad sólo se sabe que es menos de la exponencial de 1.59 × 10 ^40, que es de aproximadamente 10 a la potencia de 4,3 × 10 ^39. Dado que el número de partículas en el universo en general se considera que menos de 10 elevado a 100 (un googol), no hay esperanza de encontrar un contraejemplo explícito por búsqueda exhaustiva en la actualidad.

Tenga en cuenta que la palabra "teoría" también existe en las matemáticas, para denotar un conjunto de axiomas matemáticos, definiciones y teoremas, como en, por ejemplo, la teoría de grupos . También hay "teoremas" en la ciencia, en particular la física y en ingeniería, pero a menudo tienen las declaraciones y las pruebas en las que los supuestos físicos y la intuición juega un papel importante; los axiomas físicos en los que se basan tales "teoremas" son ellos mismos falsable.

Terminología

Los teoremas son a menudo indican con varios otros términos: el "teorema" real etiqueta está reservado para los resultados más importantes, mientras que los resultados que son menos importantes, o distinguen de otras formas, son nombrados por una terminología diferente.

• La proposición es una declaración no está asociado a ninguna teorema particular. Este término a veces connota una declaración con una prueba simple.
• La lema es un "pre-teorema", una declaración que forma parte de la demostración de un teorema más grande. La distinción entre teoremas y lemas es bastante arbitraria, ya que uno de matemático importante resultado es otra afirmación es menor. Lema de Gauss y Lema de Zorn, por ejemplo, son bastante interesante que algunos autores presentan el lema nominal sin ir en utilizarlo en la demostración de un teorema.
• La corolario es una proposición que sigue con poca o ninguna prueba de otro teorema o definición. Es decir, la proposición B es un corolario de una proposición A si B fácilmente se puede deducir de la A.
• Una reclamación es una consecuencia necesaria o independientemente interesante que puede ser parte de la prueba de otro comunicado. A pesar del nombre, los reclamos deben ser probadas.

Hay otros términos, menos comúnmente usados, que convencionalmente se adjuntan a las declaraciones probadas, por lo que ciertos teoremas se conocen por nombres históricos o consuetudinarias. Por ejemplo:

• Identidad, utilizada para teoremas que establecen una igualdad entre dos expresiones matemáticas. Los ejemplos incluyen la identidad de Euler y La identidad de Vandermonde.
• Regla, utilizado para ciertos teoremas tales como La regla de Bayes y La regla de Cramer, que establecen fórmulas útiles.
• Ley. Los ejemplos incluyen el ley de los grandes números, el ley de los cosenos, y La ley de Kolmogorov cero-uno.
• Principio. Los ejemplos incluyen Principio de Harnack, la principio del límite superior mínimo, y la encasillar principio.
• La Converse es un teorema inverso. Por ejemplo, si un teorema afirma que A es un relacionado con B, es contrario sería afirmar que B está relacionada con A. El inverso de un teorema no tiene que ser siempre cierto.

A pocos teoremas conocidos tienen incluso nombres más idiosincrásicos. La división algoritmo A teorema expresar el resultado de la división de los números naturales y los anillos más generales. La Banach-Tarski paradoja es un teorema en medir la teoría de que es paradójico en el sentido de que contradice intuiciones comunes sobre el volumen en el espacio tridimensional.

Una afirmación no demostrada de que se cree que es cierto se llama conjetura (oa veces una hipótesis, pero con un significado diferente de la que se discutió anteriormente). Para ser considerado una conjetura, una declaración general debe ser propuesto públicamente, momento en el que el nombre del proponente puede estar unido a la conjetura, al igual que con la conjetura de Goldbach . Otras conjeturas famosos incluyen el Collatz conjeturas y la Hipótesis de Riemann.

Disposición

Un teorema y su prueba son típicamente dispuestos como sigue:

Teorema (nombre de la persona que lo probó y año de descubrimiento, prueba o publicación).

Declaración del teorema.

Prueba.

Descripción de la prueba.

El final de la prueba puede ser señalado por las letras QED significado " quod erat demonstrandum "o por uno de los marcas lápida "□" o "∎" que significa "Fin de la prueba", introducido por Paul Halmos después de su uso en artículos de revistas.

El estilo exacto dependerá del autor o publicación. Muchas publicaciones proporcionan instrucciones o macros para la composición tipográfica en el estilo de la casa.

Es común que un teorema a ser precedida por definiciones que describen el significado exacto de los términos utilizados en el teorema. También es común para un teorema para ir precedido por un número de proposiciones o lemas que luego se utiliza en la prueba. Sin embargo, lemas a veces se incrustan en la demostración de un teorema, ya sea con las pruebas anidadas, o con sus pruebas presentadas después de la demostración del teorema.

Corolarios de un teorema se presentan ya sea entre el teorema y la prueba, o directamente después de la prueba. A veces corolarios tienen pruebas de su propia que explican por qué se siguen desde el teorema.

Tradiciones

Se ha estimado que más de un cuarto se han demostrado de un millón de teoremas cada año.

El bien conocido aforismo, "Un matemático es un dispositivo para dar vuelta al café en teoremas", es probablemente debido a Alfréd Rényi, aunque a menudo se atribuye a la colega de Rényi Paul Erdös (y Rényi pueden haber estado pensando en Erdős), que era famoso por los muchos teoremas que ha presentado, la número de sus colaboraciones, y su consumo de café.

La clasificación de los grupos finitos simples es considerada por algunos como la prueba más larga de un teorema; comprende decenas de miles de páginas de 500 artículos de revistas por unos 100 autores. Estos documentos se cree para dar una demostración completa, y hay varios proyectos en marcha para acortar y simplificar esta prueba.

Buscar teorema en Wikcionario, el diccionario libre.