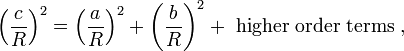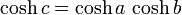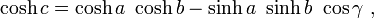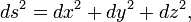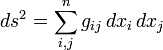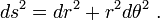Teorema de pitágoras
Antecedentes de las escuelas de Wikipedia
SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/

| Trigonometría |
|---|
| Historia Uso Funciones Generalizada Funciones inversas Otras lecturas |
| Referencia |
| Identidades Constantes Exactas Tablas trigonométricas |
| Las leyes y teoremas |
| Ley de los senos Ley de los cosenos Ley de las tangentes Ley de cotangentes Teorema de pitágoras |
| Cálculo |
| Sustitución trigonométrica Integrales de funciones Derivadas de funciones Integrales de funciones inversas |
| Geometría |
|---|
 Oxirrinco papiro (P.Oxy. I 29) que muestra un fragmento de los Elementos de Euclides |
| Historia de la geometría |
Ramas Geometría euclidiana · La geometría no-euclidiana · Geometría analítica · La geometría de Riemann · Geometría diferencial · La geometría descriptiva · La geometría algebraica |
Líneas de investigación |
Conceptos importantes Notas · Línea · Perpendicular · Paralelo · El segmento de línea · Ray · Plano · Longitud · Espacio · Volumen · Vertex · ángulo · Congruencia · Similitud · Polígono · Triángulo · Altitud · Hipotenusa · teorema de Pitágoras · Cuadrilátero · Trapecio · Kite · Paralelogramo ( Romboidal, Rectángulo, Rombo, Plaza ) · Diagonal · Simetría · curva · Círculo · Área de un círculo · Circunferencia · Diámetro · Cilindro · Esfera · Pirámide · Dimensiones ( uno, dos, tres, cuatro) |
Los geómetras Aryabhata · Ahmes · Apolonio · Arquímedes · Baudhayana · Bolyai · Brahmagupta · Euclides · Pitágoras · Khayyám · Descartes · Pascal · Euler · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · Katyayana · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · Poincaré · Sijzi · Hilbert · Minkowski · Cartan · Veblen · Sakabe Kohan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng |
En matemáticas , el teorema de Pitágoras - o teorema de Pitágoras - es una relación en la geometría euclídea entre los tres lados de un triángulo rectángulo (triángulo en ángulo recto). Por áreas, se indica:
En todo triángulo rectángulo, el área del cuadrado cuyo lado es la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de las áreas de los cuadrados cuyos lados son las dos piernas (los dos lados que se unen en una ángulo recto).
El teorema se puede escribir como una ecuación que relaciona las longitudes de los lados a, b y c, a menudo llamada la ecuación de Pitágoras:
donde c representa la longitud de la hipotenusa, y a y b representan las longitudes de los otros dos lados.
El teorema de Pitágoras es el nombre del Matemático griego Pitágoras (ca. 570 aC-495 aC aproximadamente), que por tradición se le atribuye su descubrimiento y prueba , aunque a menudo se argumenta que el conocimiento del teorema anterior a él. Hay pruebas de que Matemáticos babilónicos entendieron la fórmula, aunque hay poca evidencia sobreviviente que lo utilizaron en un marco matemático.
El teorema tiene numerosas pruebas , posiblemente más que cualquier otro teorema matemático. Estos son muy diversas, incluyendo tanto pruebas geométricas y pruebas algebraicas, con algunos que datan de miles de años. El teorema se puede generalizar de varias maneras, incluyendo espacios de dimensiones superiores, a los espacios que no son euclidiana, a objetos que no son triángulos rectángulos, y de hecho, a los objetos que no son triángulos en absoluto, pero n sólidos -dimensionales. El teorema de Pitágoras ha despertado el interés fuera de las matemáticas como un símbolo de abstruseness matemática, mística, o el poder intelectual; referencias populares de la literatura, obras de teatro, musicales, canciones, sellos y dibujos animados abundan.
Otras formas
Como se ha señalado en la introducción, si c denota la longitud de la hipotenusa y a y b denotar las longitudes de los otros dos lados, el teorema de Pitágoras se puede expresar como la ecuación de Pitágoras:
Si la longitud de ambos a y b son conocidos, entonces c se puede calcular como sigue:
Si la longitud de la hipotenusa c y una pierna (A o B) son conocidos, entonces la longitud de la otra pierna se puede calcular con las ecuaciones siguientes:
o
La ecuación de Pitágoras relaciona los lados de un triángulo rectángulo de una manera simple, de modo que si las longitudes de dos lados se conocen la longitud del tercer lado se puede encontrar. Otro corolario del teorema es que en cualquier triángulo rectángulo, la hipotenusa es mayor que cualquiera de las piernas, pero menor que la suma de ellos.
Una generalización de este teorema es la ley de los cosenos, lo que permite el cálculo de la longitud del tercer lado de cualquier triángulo, dadas las longitudes de dos lados y el tamaño del ángulo entre ellos. Si el ángulo entre los lados es un ángulo recto, la ley de los cosenos reduce a la ecuación de Pitágoras.
Pruebas
Este teorema puede tener pruebas más conocidas que cualquier otro (la ley de reciprocidad cuadrática ser otro competidor para esa distinción); el libro El Pitágoras Proposición contiene 370 pruebas.
Prueba usando triángulos semejantes

Esta prueba se basa en la proporcionalidad de los lados de dos triángulos semejantes, es decir, en el hecho de que la proporción de cualquiera de los dos lados correspondientes de triángulos semejantes es la misma, independientemente del tamaño de los triángulos.
Sea ABC representan un triángulo rectángulo, con el ángulo recto se encuentra en C, como se muestra en la figura. Queremos llamar la altitud del punto C, y llamada H su intersección con el lado AB. Punto H divide la longitud de la hipotenusa c en partes D y E. El nuevo ACH triángulo es similar al triángulo ABC, porque ambos tienen un ángulo recto (por definición de la altitud), y comparten el ángulo en A, lo que significa que el tercer ángulo será el mismo en ambos triángulos, así, marcados como θ en la figura. Por un razonamiento similar, el triángulo CBH es también similar a ABC. La prueba de similitud de los triángulos requiere la Triángulo postulado: la suma de los ángulos de un triángulo es de dos ángulos rectos, y es equivalente a la postulado de las paralelas. La similitud de los triángulos conduce a la igualdad de las relaciones entre los lados correspondientes:
El primer resultado iguala el coseno de cada θ ángulo y el segundo resultado iguala el senos.
Estas relaciones se pueden escribir como:
Sumando estas dos igualdades, obtenemos
que, poner en orden, es el teorema de Pitágoras:
El papel de esta prueba en la historia es objeto de mucha especulación. La pregunta de fondo es ¿por Euclides no utilizó esta prueba, pero inventó otro. Una conjetura es que la prueba por triángulos semejantes implicó una teoría de las proporciones, un tema no se ha discutido hasta más tarde en los Elementos, y que la teoría de las proporciones necesita un mayor desarrollo en ese momento.
La demostración de Euclides

En resumen, aquí es cómo la prueba en los de Euclides Elementos ingresos. La gran plaza se divide en un rectángulo izquierda y derecha. Un triángulo está construida que tiene la mitad del área del rectángulo izquierdo. Luego, otro triángulo está construida que tiene la mitad del área del cuadrado en el extremo izquierdo lado. Estos dos triángulos se muestran para ser congruentes, lo que demuestra esta plaza tiene la misma área que el rectángulo izquierdo. Este argumento es seguido por una versión similar para el rectángulo de la derecha y de la plaza restante. Poner los dos rectángulos juntos para reformar el cuadrado de la hipotenusa, su área es la misma que la suma de la zona de los otros dos cuadrados. Los detalles están al lado.
Sean A, B, C el vértices de un triángulo rectángulo, con un ángulo recto en A. Caída de una perpendicular de la A a la cara opuesta a la hipotenusa en el cuadrado de la hipotenusa. Esa línea divide el cuadrado de la hipotenusa en dos rectángulos, cada uno tiene la misma área como uno de los dos cuadrados de los catetos.
Para la prueba formal, requerimos cuatro primaria lemas:
- Si dos triángulos tienen dos lados del uno igual a dos lados de la otra, cada una para cada uno, y los ángulos incluidos por esos lados iguales, entonces los triángulos son congruentes ( lado-ángulo-lado).
- El área de un triángulo es la mitad del área de cualquier paralelogramo en la misma base y que tiene la misma altitud.
- El área de un rectángulo es igual al producto de dos lados adyacentes.
- El área de un cuadrado es igual al producto de dos de sus lados (de 3 siguiente).
A continuación, cada cuadrado superior está relacionado con un congruentes triángulo con otro triángulo relacionado a su vez a uno de dos rectángulos que componen el cuadrado inferior.

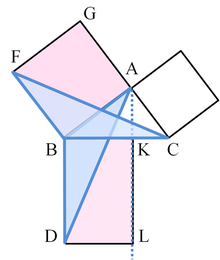
La prueba es el siguiente:
- Deje ACB sea un triángulo rectángulo con CAB ángulo recto.
- En cada uno de los lados BC, AB y CA, plazas se dibujan, CBDE, BAGF y ACIH, en ese orden. La construcción de cuadrados requiere los teoremas inmediatamente anteriores en Euclides, y depende del postulado de las paralelas.
- Desde A, trazar una línea paralela a BD y CE. Será perpendicularmente intersectar BC y DE en K y L, respectivamente.
- Únete CF y AD, para formar el BCF triángulos y BDA.
- Los ángulos CAB y la bolsa son dos ángulos rectos; Por lo tanto, C, A, y G son colineales . Del mismo modo para B, A, y H.
- Ángulos CDB y FBA son dos ángulos rectos; Por lo tanto, el ángulo ABD es igual al ángulo FBC, ya que ambos son la suma de un ángulo recto y el ángulo ABC.
- Desde AB es igual a FB y BD es igual a BC, triángulo ABD debe ser congruente con el triángulo FBC.
- Desde AKL es una línea recta, paralela a BD, entonces rectángulo BDLK tiene dos veces el área del triángulo ABD porque comparten la base de BD y tienen la misma altitud BK, es decir, una línea normal a su base común, la conexión de las líneas paralelas BD y AL. (Lema 2)
- Como C es colineal con A y G, BAGF cuadrado debe ser dos veces en el área de triángulo FBC.
- Por lo tanto BDLK rectángulo debe tener la misma zona que Plaza BAGF = AB 2.
- Del mismo modo, se puede demostrar que CKLE rectángulo debe tener la misma zona que Plaza ACIH = AC 2.
- La incorporación de estos dos resultados, AB 2 + 2 = AC BD × BK + KL × KC
- Desde BD = KL, BD × BK + KL × KC = BD (BK + KC) = BD × BC
- Por lo tanto AB 2 + 2 AC = BC 2, ya CBDE es un cuadrado.
Esta prueba, que aparece en los Elementos de Euclides como el de la Proposición 47 en el libro 1, demuestra que el área del cuadrado de la hipotenusa es la suma de las áreas de las otras dos plazas. Esto es muy distinto de la prueba por la similitud de los triángulos, que se conjeturó que ser la prueba de que Pitágoras utiliza.
Demostración por reordenamiento
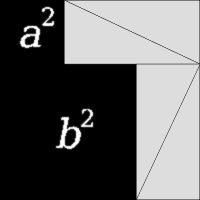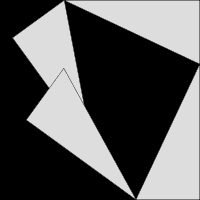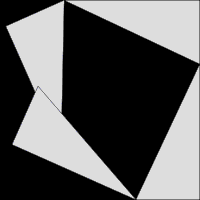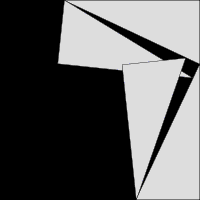
La animación de la izquierda consiste en una gran plaza, lado a + b, que contiene cuatro triángulos idénticos derechos. Los triángulos se muestran en dos modalidades, la primera de lo que deja dos cuadrados a 2 y b 2 descubiertas, el segundo de lo que deja c cuadrado de 2 descubierto. El área abarcada por el cuadrado exterior nunca cambia, y el área de los cuatro triángulos es el mismo al comienzo y al final, por lo que las áreas de cuadrados negros debe ser igual, por lo tanto, un 2 + b 2 = c 2.
Una segunda prueba está dada por la animación medio. Una gran plaza se forma con zona de c 2, a partir de cuatro triángulos rectángulos idénticos con lados a, byc, armarios alrededor de una pequeña plaza central. Entonces dos rectángulos se forman con los lados a y b moviendo los triángulos. La combinación de la plaza más pequeña con estos rectángulos produce dos cuadrados de zonas un 2 y B 2, que deben tener la misma superficie que el cuadrado grande inicial.
La tercera imagen, más a la derecha también da una prueba. Las dos casillas superiores se dividen como se muestra por el sombreado azul y verde, en trozos que cuando reordenado se pueden hacer para caber en la plaza inferior de la hipotenusa - o por el contrario la gran plaza se puede dividir como se muestra en piezas que llenan los otros dos . Esto muestra el área del cuadrado grande es igual a la de los dos más pequeños.
 |  | 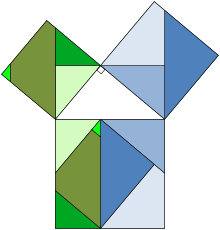 |
Pruebas algebraicas

El teorema se puede demostrar algebraicamente utilizando cuatro copias de un triángulo rectángulo de lados a, byc, dispuestos en el interior de un cuadrado de lado c como en la mitad superior de la figura. Los triángulos son semejantes con zona 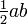 , Mientras que el pequeño cuadrado tiene lado b - a y el área (b - a) 2. Por tanto, el área del cuadrado grande es
, Mientras que el pequeño cuadrado tiene lado b - a y el área (b - a) 2. Por tanto, el área del cuadrado grande es
Pero este es un cuadrado de lado c y el área c 2, por lo que
Una prueba similares utiliza cuatro copias del mismo triángulo dispuestas simétricamente alrededor de un cuadrado de lado c, como se muestra en la parte inferior del diagrama. Esto se traduce en un cuadrado más grande, con el lado a + b y la zona (a + b) 2. Los cuatro triángulos y el lado cuadrado c deben tener la misma superficie que el cuadrado más grande,
dando

Una prueba relacionada fue publicado por el ex presidente estadounidense James A. Garfield . En lugar de un cuadrado que utiliza una trapezoide, que puede ser construido a partir de la plaza en la segunda de las pruebas anteriores por bisectriz lo largo de una diagonal del cuadrado interior, para dar el trapezoide como se muestra en el diagrama. La área del trapecio se puede calcular a ser la mitad del área del cuadrado, es decir
La plaza interior se redujo a la mitad del mismo modo, y sólo hay dos triángulos por lo que la prueba procede como antes excepto por un factor de  , Que se elimina mediante la multiplicación por dos para dar el resultado.
, Que se elimina mediante la multiplicación por dos para dar el resultado.
Prueba usando diferenciales
Uno puede llegar al teorema de Pitágoras mediante el estudio de cómo los cambios en un lado producen un cambio en la hipotenusa y el empleo de cálculo .
El triángulo ABC es un triángulo rectángulo, como se muestra en la parte superior del diagrama, con la hipotenusa BC. Al mismo tiempo las longitudes de triángulo se miden como se muestra, con la hipotenusa de longitud y, el AC lado de la longitud x y el lado AB de longitud a, como se ve en la parte inferior del diagrama.
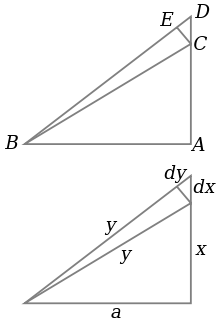
Si x se incrementa en una pequeña cantidad dx mediante la extensión de la AC lado ligeramente a D, a continuación, y también aumenta por dy. Estos forman dos lados de un triángulo, CDE, que (con E elige de manera CE es perpendicular a la hipotenusa) es un triángulo rectángulo aproximadamente similar a ABC. Por lo tanto las proporciones de sus lados deben ser iguales, es decir:
Esto puede ser reescrita como sigue:
Esta es una ecuación diferencial que se resuelve para dar
Y la constante se puede deducir de x = 0, y = A para dar la ecuación
Esto es más de una prueba intuitiva que un formal de uno: se puede hacer más riguroso si los límites adecuados se utilizan en lugar de dx y dy.
Conversar
El inverso del teorema también es cierto:
Para cualquiera de los tres números positivos a, b, y c de modo que un 2 + b 2 = c 2, existe un triángulo con lados a, b y c, y cada uno de tales triángulo tiene un ángulo recto entre los lados de longitudes a y b .
Una declaración alternativa es:
Para cualquier triángulo con lados a, b, c, si un 2 + b 2 = c 2, entonces el ángulo entre A y B mide 90 °.
Esta contrario también aparece en Elementos de Euclides (Libro I, la Proposición 48):
"Si en un triángulo el cuadrado de uno de los lados es igual a la suma de los cuadrados de los otros dos lados del triángulo, entonces el ángulo comprendido por los dos lados restantes del triángulo es correcto."
Se puede probar con el ley de los cosenos o de la siguiente manera:
Sea ABC un triángulo con lados de longitudes a, b, y c, con un 2 + b 2 = c 2. Construir un segundo triángulo con lados de longitud a y b que contiene un ángulo recto. Por el teorema de Pitágoras, se sigue que la hipotenusa de este triángulo tiene longitud c = √ un 2 + b 2, la misma que la hipotenusa del triángulo primero. Desde ambos lados triángulos "son las mismas longitudes a, b, c, los triángulos son congruentes y debe tener los mismos ángulos. Por lo tanto, el ángulo entre el lado de longitudes a y b en el triángulo original es un ángulo recto.
La prueba anterior de la inversa hace uso de la propia Teorema de Pitágoras. Lo contrario también puede ser probado sin asumir el Teorema de Pitágoras.
La corolario inverso del teorema de Pitágoras es un medio sencillo de determinar si un triángulo es recto, obtuso o agudo, de la siguiente manera. Sea C elegido para ser el más largo de los tres lados y a + b> c (de lo contrario no hay triángulo de acuerdo con la desigualdad triangular). Las siguientes declaraciones se aplican:
- Si a 2 + b 2 = c 2, entonces el triángulo es correcto.
- Si a 2 + b 2> c 2, entonces el triángulo es agudo.
- Si a <c 2 2 + b 2, entonces el triángulo es obtuso.
Edsger Dijkstra ha declarado esta proposición sobre triángulos agudos, a la derecha, y obtusos en este idioma:
- sgn (α + β - γ) = sgn (a 2 + b 2 - c 2),
donde α es el ángulo opuesto al lado A, β es el ángulo opuesto al lado b, γ es el ángulo opuesto al lado c, y sgn es la firmar función.
Consecuencias y usos del teorema
Ternas pitagóricas
A Pitágoras triple tiene tres números enteros positivos a, b, y c, de manera que un 2 + b 2 = c 2. En otras palabras, una de Pitágoras de triple representa las longitudes de los lados de un triángulo rectángulo, donde los tres lados tienen longitudes de números enteros. La evidencia de los monumentos megalíticos de Europa del Norte muestra que tales triples eran conocidos antes del descubrimiento de la escritura. Un triple Tal es comúnmente escrito (a, b, c). Algunos ejemplos bien conocidos son (3, 4, 5) y (5, 12, 13).
Una primitiva de Pitágoras triple es una en la que a, b y c son primos entre sí (el máximo común divisor de a, b y c es 1).
La siguiente es una lista de ternas pitagóricas primitivas con valores inferiores a 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77 , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Longitudes inconmensurables
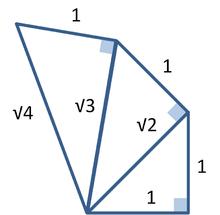
Una de las consecuencias del teorema de Pitágoras es que los segmentos de línea cuyas longitudes son inconmensurables (por lo que la relación de los cuales no es un número racional ) se puede construir usando una regla y un compás . Teorema de Pitágoras permite la construcción de longitudes inconmensurables porque la hipotenusa de un triángulo está relacionado con los lados por la raíz cuadrada operación.
La figura de la derecha muestra cómo construir segmentos de línea cuyas longitudes son en la relación entre la raíz cuadrada de cualquier número entero positivo. Cada triángulo tiene un lado (con la etiqueta "1") que es la unidad elegida para la medición. En cada triángulo rectángulo, el teorema de Pitágoras establece la longitud de la hipotenusa en términos de esta unidad. Si una hipotenusa está relacionada con la unidad por la raíz cuadrada de un número entero positivo que no es un cuadrado perfecto, que es una realización de una longitud inconmensurable con la unidad, tales como √ 2, 3 √, √ 5. Para más detalles, consulte Cuadrar irracional.
Longitudes inconmensurables en conflicto con el concepto de la escuela pitagórica de los números como sólo números enteros. La escuela pitagórica tratado proporciones mediante la comparación de múltiplos enteros de una subunidad común. Según una leyenda, Hipaso de Metaponto (ca. 470 aC) se ahogó en el mar para dar a conocer la existencia de lo irracional o inconmensurables.
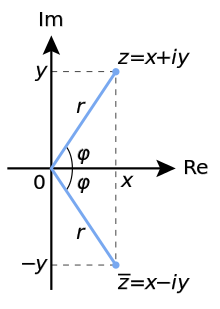
Los números complejos
Para cualquier número complejo
el valor absoluto o módulo viene dado por
Así las tres cantidades, r, x e y están relacionadas por la ecuación de Pitágoras,
Tenga en cuenta que r se define como un número positivo o cero, pero x e y pueden ser negativos, así como positivo. Geométricamente r es la distancia de la z de cero o el origen O en el plano complejo .
Esto se puede generalizar para encontrar la distancia entre dos puntos, z 1 y z 2 dicen. La distancia requerida viene dada por
así que de nuevo están relacionados por una versión de la ecuación de Pitágoras,
Distancia euclídea en varios sistemas de coordenadas
La fórmula de la distancia en coordenadas cartesianas se deriva de la teorema de Pitágoras. Si (x 1, y 1) y (x 2, y 2) son puntos en el plano, entonces la distancia entre ellos, también llamado el La distancia euclídea, está dada por
Más en general, en euclidiano n-espacio , la distancia euclidiana entre dos puntos, 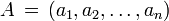 y
y 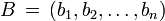 , Se define, por generalización del teorema de Pitágoras, como:
, Se define, por generalización del teorema de Pitágoras, como:
Si no se usan coordenadas cartesianas, por ejemplo, si las coordenadas polares se utilizan en dos dimensiones o, en términos más generales, si, se utilizan coordenadas curvilíneas, las fórmulas que expresan la distancia euclídea son más complicados que el teorema de Pitágoras, pero se pueden derivar de ella. Un ejemplo típico donde la distancia en línea recta entre dos puntos se convierte en coordenadas curvilíneas se puede encontrar en el aplicaciones de polinomios de Legendre en la física. Las fórmulas pueden ser descubiertos usando el teorema de Pitágoras con las ecuaciones que relacionan las coordenadas curvilíneas a coordenadas cartesianas. Por ejemplo, las coordenadas polares (r, θ) se pueden introducir como:
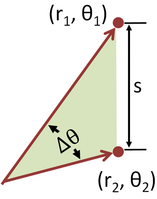
Luego, dos puntos, con locales (r 1, θ 1) y (r 2, θ 2) están separados por una distancia s:
Realización de las plazas y la combinación de términos, la fórmula de Pitágoras para la distancia en coordenadas cartesianas produce la separación en coordenadas polares como:
usando el trigonométrica de producto a suma fórmulas. Esta fórmula es la ley de los cosenos , a veces llamado el Teorema de Pitágoras generalizado. A partir de este resultado, para el caso en que los radios de los dos lugares son en ángulo recto, el cerrado ángulo θ Δ = π / 2, y el formulario correspondiente al teorema de Pitágoras se recuperaron: 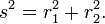 El teorema de Pitágoras, válido para triángulos rectángulos, por lo tanto, es un caso especial de la ley más general de los cosenos, válido por triángulos arbitrarios.
El teorema de Pitágoras, válido para triángulos rectángulos, por lo tanto, es un caso especial de la ley más general de los cosenos, válido por triángulos arbitrarios.
Identidad trigonométrica de Pitágoras
En un triángulo rectángulo de lados a, b y c hipotenusa, trigonometría determina la seno y el coseno del ángulo θ entre el lado A y la hipotenusa como:
Desde que sigue:
donde el último paso se aplica el teorema de Pitágoras. Esta relación entre el seno y el coseno a veces se llama la identidad trigonométrica pitagórica fundamental. En triángulos semejantes, las proporciones de los lados son iguales, independientemente del tamaño de los triángulos, y dependen de los ángulos. En consecuencia, en la figura, el triángulo con la hipotenusa del tamaño de la unidad tiene lado opuesto de θ pecado tamaño y el lado adyacente de cos θ tamaño en unidades de la hipotenusa.
Relación con el producto vectorial
El teorema de Pitágoras relaciona el producto vectorial y producto escalar de una manera similar:
Esto se puede ver a partir de las definiciones del producto cruz y producto de punto, como se
con n una unidad normal tanto a como b vector. La relación se desprende de estas definiciones y la identidad trigonométrica de Pitágoras.
Esto también puede ser utilizado para definir el producto cruzado. Reorganizando la siguiente ecuación se obtiene
Esto puede ser considerado como una condición sobre el producto cruzado y así parte de su definición, por ejemplo, en siete dimensiones.
Las generalizaciones
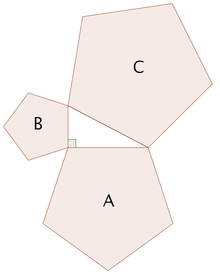
Cifras similares en los tres lados
Una generalización del teorema de Pitágoras se extiende más allá de las áreas de cuadrados de los tres lados para cifras similares se conocía por Hipócrates de Chios en el siglo V aC, y fue incluido por Euclides en sus Elementos :
Si uno erige cifras similares (ver la geometría euclidiana ) con lados correspondientes a los lados de un triángulo rectángulo, entonces la suma de las áreas de los que están en los dos lados menores es igual al área de la que está en el lado más grande.
Esta ampliación supone que los lados del triángulo original son los lados correspondientes de las tres figuras congruentes (por lo que las relaciones comunes de lados entre las cifras similares son a: b:. C Si bien la demostración de Euclides sólo aplica a los polígonos convexos, el teorema se aplica también a polígonos cóncavos e incluso a las figuras similares que han curvas límites (pero aún con una parte de límite de una figura ser el lado del triángulo original).
La idea básica detrás de esta generalización es que el área de una figura plana es proporcional al cuadrado de cualquier dimensión lineal, y en particular es proporcional al cuadrado de la longitud de cualquier lado. Por lo tanto, si las cifras similares con las zonas A, B y C se erigen en los lados con longitudes correspondiente a, b y c, entonces:
Pero, por el teorema de Pitágoras, a 2 + b 2 = c 2, por lo que A + B = C.
Por el contrario, si podemos probar que A + B = C durante tres cifras similares sin necesidad de utilizar el teorema de Pitágoras, entonces podemos trabajar hacia atrás para construir una demostración del teorema. Por ejemplo, el triángulo centro de partida puede ser replicado y usado como un triángulo C sobre su hipotenusa, y dos triángulos rectángulos similares (A y B) construidos en los otros dos lados, formada dividiendo el triángulo central por su altitud. La suma de las áreas de los dos triángulos más pequeños, por tanto, es el de la tercera, por tanto, A + B = C e invertir la lógica anterior conduce a el teorema de Pitágoras a 2 + b 2 = c 2.
Ley de los cosenos
El teorema de Pitágoras es un caso especial del teorema más general que relaciona las longitudes de los lados de cualquier triángulo, la ley de los cosenos:
donde θ es el ángulo entre los lados a y b.
Cuando θ es 90 grados, entonces cos θ = 0, y la fórmula se reduce a el teorema de Pitágoras usual.
Triángulo Arbitraria
En cualquier ángulo seleccionado de un triángulo general de lados a, b, c, inscribir un triángulo isósceles de tal manera que los ángulos iguales en su θ base son el mismo que el ángulo seleccionado. Supongamos que el θ ángulo seleccionado está enfrente de la cara de la etiqueta c. La inscripción de la forma de triángulo isósceles triángulo ABD con ángulo θ lado opuesto una y con r lado a lo largo c. Un segundo triángulo se forma con un ángulo θ lado opuesto B y un lado de longitud a lo largo de s c, como se muestra en la figura. TabIt Ibn Qorra declaró que los lados de los tres triángulos estaban relacionados como:
A medida que el ángulo θ se aproxima a π / 2, la base de la triángulo isósceles se estrecha, y r y s longitudes solapan menos y menos. Cuando θ = π / 2, ADB se convierte en un triángulo, r + s = derecha c, y se recuperó el teorema de Pitágoras el original ".
Una prueba observa que el triángulo ABC tiene los mismos ángulos como triángulo ABD, pero en orden inverso. (Los dos triángulos compartir el ángulo en el vértice B, ambos contienen el ángulo θ, y así también tener el mismo tercer ángulo por el postulado triángulo.) Por consiguiente, ABC es similar a la reflexión de la ABD, el DBA triángulo en el panel inferior. Tomando la relación de lados opuesto y adyacente a θ,
Del mismo modo, para la reflexión de la otra triángulo,
Borrado de fracciones y la adición de estas dos relaciones:
el resultado requerido.
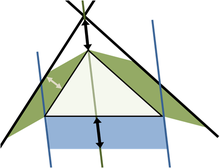
Triángulos generales utilizando paralelogramos
Una generalización más se aplica a triángulos que no son triángulos rectángulos, paralelogramos utilizando en los tres lados en lugar de cuadrados. (Cuadrados son un caso especial, por supuesto). La figura superior muestra que para un triángulo escaleno, el área del paralelogramo en el lado más largo es la suma de las áreas de los paralelogramos en los otros dos lados, siempre que el paralelogramo en el lado largo se construye como se indica (las dimensiones marcadas con las flechas son la misma, y determinar los lados del paralelogramo inferior). Esta sustitución de las plazas con paralelogramos tiene un parecido evidente con el teorema original de Pitágoras, y fue considerado una generalización por Pappus de Alejandría en 4 AD
La figura inferior muestra los elementos de la prueba. Centrarse en el lado izquierdo de la figura. El paralelogramo verde de la izquierda tiene la misma área que la izquierda, la porción azul del paralelogramo inferior debido a que ambos tienen la misma base b y la altura h. Sin embargo, el paralelogramo verde de la izquierda también tiene la misma área que el paralelogramo verde de la izquierda de la figura superior, debido a que tienen la misma base (el lado izquierdo superior del triángulo) y la misma altura normal a ese lado del triángulo. Repitiendo el argumento para el lado derecho de la figura, el paralelogramo inferior tiene la misma área que la suma de los dos paralelogramos verdes.
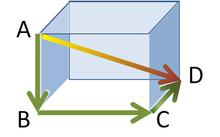
Geometría del espacio
En términos de la geometría sólida, el teorema de Pitágoras se puede aplicar a las tres dimensiones de la siguiente manera. Considere un sólido rectangular, como se muestra en la figura. La longitud de BD diagonal Se encuentra desde el teorema de Pitágoras como:
donde estos tres lados forman un triángulo rectángulo. Uso de BD diagonal horizontal y el borde vertical AB, la longitud de la diagonal AD entonces es encontrada por una segunda aplicación del teorema de Pitágoras como:
o, de hacerlo todo en un solo paso:
Este resultado es la expresión tridimensional para la magnitud de un vector v (la AD diagonal) en términos de sus componentes ortogonales {v} (k los tres lados perpendiculares entre sí):
Esta formulación de un solo paso puede ser visto como una generalización del teorema de Pitágoras a las dimensiones más altas. Sin embargo, este resultado es realmente sólo la aplicación repetida del teorema de Pitágoras el original a una sucesión de triángulos rectángulos en una secuencia de planos ortogonales.
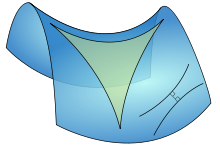
Una generalización sustancial del teorema de Pitágoras a tres dimensiones es teorema de De Gua, llamado así por Jean-Paul de Gua de Malves: Si un tetraedro tiene una esquina en ángulo recto (como un rincón de un cubo ), entonces el cuadrado de la superficie de la cara opuesta de la esquina en ángulo recto es la suma de los cuadrados de las áreas de la otra tres caras. Este resultado puede generalizarse como en el "teorema de Pitágoras n -dimensional":
Dejarser vectores ortogonales en ℝ n. Considere la n-dimensional simplex S con vértices
. (Piense en el (n - 1) simplex-dimensional con vértices
no incluyendo el origen como el "hipotenusa" de S y el resto (n - 1) caras dimensionales de S como sus "patas"), entonces el cuadrado del volumen de la hipotenusa de S es la suma de los cuadrados de la. volúmenes de los n piernas.
Esta declaración se ilustra en tres dimensiones por el tetraedro en la figura. El "hipotenusa" es la base del tetraedro en la parte posterior de la figura, y las "patas" son los tres lados que emanan desde el vértice en el primer plano. Como la profundidad de la base desde el vértice aumenta, el área de las "patas" aumenta, mientras que la de la base es fija. El teorema sugiere que cuando esta profundidad se encuentra en la creación de valor un vértice derecho, se aplica la generalización del teorema de Pitágoras. En una redacción diferente:
Dado unn-rectangularnsimplex-dimensional, la plaza de la (n- 1) -contenido de lafaceta oponerse el vértice derecho será igual a la suma de los cuadrados de los (n- 1) -Contenido de las facetas restantes.
Espacios interiores de productos
El teorema de Pitágoras se puede generalizar a espacios interiores de productos, que son generalizaciones de los 2-dimensionales y 3-dimensionales familiares espacios euclídeos . Por ejemplo, una función puede ser considerada como un vector con un número infinito de componentes en un espacio con producto interno, como en análisis funcional.
En un espacio con producto interno, el concepto de perpendicularidad se sustituye por el concepto de ortogonalidad: dos vectores v y w son ortogonales si su producto interior 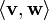 es cero. La producto interno es una generalización de la producto escalar de los vectores. El producto escalar se llama el estándar de producto interior o la euclidiana producto interno. Sin embargo, otros productos internos son posibles.
es cero. La producto interno es una generalización de la producto escalar de los vectores. El producto escalar se llama el estándar de producto interior o la euclidiana producto interno. Sin embargo, otros productos internos son posibles.
El concepto de longitud se sustituye por el concepto de lanorma ||v|| de un vectorv, define como:
En un espacio-producto interno, elteorema de Pitágorasestablece que para cualquier par de vectores ortogonalesvywtenemos
Aquí los vectores v y w son semejantes a los lados de un triángulo rectángulo con hipotenusa propuesta por el vector suma v + w . Esta forma del teorema de Pitágoras es una consecuencia de las propiedades del producto interior:
donde los productos interiores de los términos cruzados son cero, debido a la ortogonalidad.
Una generalización adicional de la teorema de Pitágoras en un espacio con producto interno a vectores no ortogonales es la ley del paralelogramo:
que dice que dos veces la suma de los cuadrados de las longitudes de los lados de un paralelogramo es la suma de los cuadrados de las longitudes de las diagonales. Cualquier norma que cumple esta igualdad es ipso facto una norma que corresponde a un producto interno.
La identidad de Pitágoras se puede extender a sumas de más de dos vectores ortogonales. Si v 1 , v 2 , ..., v n son vectores ortogonales dos a dos en un espacio-producto interno, entonces la aplicación del teorema de Pitágoras a pares sucesivos de estos vectores (como se describe para 3-dimensiones en la sección sobre la geometría sólida ) resulta en la ecuación
La identidad de Parseval es una generalización, además, que considera infinitas sumas de vectores ortogonales.
Para el producto interior
(Bes unhermíticamatriz definida positiva yu *latranspuesta conjugada deu) el teorema de Pitágoras es:
dondePes unaproyección que satisface:
El mapa lineal:
a continuación, es unaproyección ortogonal.
La geometría no-euclidiana
El teorema de Pitágoras se deriva de los axiomas de lageometría euclidiana, y de hecho, el teorema de Pitágoras dada anteriormente no se sostiene en un geometría no euclidiana.(El teorema de Pitágoras se ha demostrado, de hecho, serequivalente a las paralelas de Euclides (Quinta) Postulado). En otras palabras, en la geometría no euclidiana, la relación entre los lados de un triángulo deben tener necesariamente una forma no de Pitágoras. Por ejemplo, en geometría esférica, los tres lados del triángulo rectángulo (por ejemploun,b, yc) que delimita un octante de la unidad esfera tiene una longitud igual a π / 2, y todos sus ángulos son ángulos rectos, lo que viola el teorema de Pitágoras porqueun 2+b 2≠c 2.
Aquí dos casos de la geometría no euclidiana son considered- geometría esférica y geometría plano hiperbólico; en cada caso, como en el caso euclidiana para triángulos no rectos, el resultado reemplazando el teorema de Pitágoras se deduce de la ley de los cosenos apropiado.
Sin embargo, el teorema de Pitágoras sigue siendo cierto en la geometría hiperbólica y geometría elíptica si la condición de que el triángulo tenga razón se sustituye con la condición de que dos de los ángulos suman la tercera, digamos A + B = C . Los lados se relacionan a continuación, de la siguiente manera: la suma de las áreas de los círculos con diámetros de un y b es igual al área del círculo con el diámetro c .
La geometría esférica
Para cualquier triángulo rectángulo en una esfera de radioR(por ejemplo, si γ en la figura es un ángulo recto), con ladosun,b,c, la relación entre los lados toma la forma:
Esta ecuación se puede derivar como un caso especial de laley de los cosenos esférica que se aplica a todos los triángulos esféricos:
Mediante el uso de la serie de Maclaurin para la función coseno, cos x ≈ 1 - x 2 / 2 , se puede demostrar que a medida que el radio R se aproxima al infinito y los argumentos a / R, b / R y C / R tienden a cero, la esférica relación entre los lados de un triángulo rectángulo se aproxima a la forma del teorema de Pitágoras. Sustituyendo la ecuación cuadrática aproximada para cada uno de los cosenos en la relación esférica para un triángulo rectángulo:
Multiplicando las cantidades entre paréntesis, el teorema de Pitágoras se recupera para grandes radiosR:
donde lostérminos de orden superiorse vuelven insignificantemente pequeña comoRse hace grande.
Geometría hiperbólica
Para un triángulo rectángulo en la geometría hiperbólica con ladosa,b,c, y con el ladocfrente a un ángulo recto, la relación entre los lados de la forma:
donde cosh es el coseno hiperbólico. Esta fórmula es una forma especial de la ley de los cosenos hiperbólicos que se aplica a todos los triángulos hiperbólicas:
con γ el ángulo en el vértice opuesto al ladoc.
Mediante el uso de laserie de Maclaurinpara el coseno hiperbólico,coshx≈ 1 +x 2/ 2, se puede demostrar que como un triángulo hiperbólico se hace muy pequeña (es decir, comoun,b, yctodo enfoque cero), la relación hiperbólica de un triángulo rectángulo se acerca a la forma del teorema de Pitágoras.
Geometría diferencial
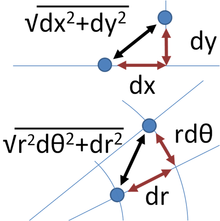
A nivel infinitesimal, en un espacio tridimensional, el teorema de Pitágoras describe la distancia entre dos puntos infinitesimalmente separados como:
con ds el elemento de la distancia y ( dx , dy , dz ) los componentes del vector de la separación de los dos puntos. Tal espacio se llama un espacio euclidiano . Sin embargo, una generalización de esta expresión útil para las coordenadas generales (no sólo cartesiana) y espacios en general (no sólo euclidiana) toma la forma:
donde g ij es llamado el tensor métrico. Puede ser una función de la posición. Tal espacios curvos incluyen la geometría de Riemann como un ejemplo general. Esta formulación también se aplica a un espacio euclidiano utilizando las coordenadas curvilíneas. Por ejemplo, en coordenadas polares :
Historia
Existe un debate si el teorema de Pitágoras fue descubierto una vez, o muchas veces en muchos lugares.
La historia del teorema se puede dividir en cuatro partes: el conocimiento deternas pitagóricas, el conocimiento de la relación entre los lados de untriángulo rectángulo, el conocimiento de las relaciones entre los ángulos adyacentes, y pruebas del teorema dentro de algún sistema deductivo.
Bartel Leendert van der Waerden (1903-1996) conjeturó que ternas pitagóricas fueron descubiertos algebraicamente por los babilonios. Escrito entre 2000 y 1786 aC, el Imperio Medio egipcio papiro de Berlín 6619 incluye un problema cuya solución es la terna pitagórica 6: 8: 10, pero el problema no menciona un triángulo. La Mesopotamia tableta Plimpton 322 , escrito entre 1790 y 1750 aC, durante el reinado de Hammurabi el Grande, contiene muchas entradas estrechamente relacionados con ternas pitagóricas.
En la India , la Baudhayana Sulba Sutra , las fechas de los cuales se dan indistintamente como entre el el siglo segundo siglo antes de Cristo y el octavo, contiene una lista de ternas pitagóricas descubrió algebraica, una declaración del teorema de Pitágoras, y geométrica prueba de Pitágoras teorema para un isósceles triángulo rectángulo. La Apastamba Sulba Sutra ( ca. 600 aC) contiene una prueba numérica del teorema de Pitágoras en general, utilizando un cálculo área. Van der Waerden cree que "fue sin duda basa en tradiciones anteriores". Boyer (1991) piensa que los elementos que se encuentran en el Sulba-sũtram pueden ser de derivación mesopotámica.
Con contenidos conocidos mucho antes, pero en los textos sobrevivientes datan de aproximadamente el siglo I antes de Cristo, el chino, el texto Zhou Bi Suan Jing (周髀算经), ( La aritmética clásico del Gnomon y las trayectorias circulares del Cielo ) da una razón para el teorema de Pitágoras para la (3, 4, 5) de triángulo en China se le llama el "Gougu Teorema" (勾股定理). Durante el Dinastía Han (202 aC a 220 dC), triples pitagóricos aparecen en Los Nueve Capítulos sobre la Matemática Arte , junto con una mención de triángulos rectángulos. Algunos creen que el teorema se presentó por primera vez en China, donde es conocido alternativamente como el "Shang Gao Teorema" (商高定理), llamado así por el duque de astrónomo y matemático de Zhou, cuyo razonamiento integrado por la mayor parte de lo que fue en el Zhou Bi Suan Jing .
Pitágoras , cuyas fechas son comúnmente dada como 569 a 475 antes de Cristo, utiliza métodos algebraicos para construir ternas pitagóricas, de acuerdo con el comentario de Proclo sobre Euclides . Proclo, sin embargo, escribió entre 410 y 485 dC. De acuerdo a Sir Thomas L. Heath (1861-1940), no existe una atribución específica del teorema de Pitágoras en la literatura griega que sobrevive de los cinco siglos después de Pitágoras vivió. Sin embargo, cuando autores como Plutarco y Cicerón atribuye el teorema de Pitágoras, lo hicieron de una manera que sugiere que la atribución era ampliamente conocido y indudable. "Ya sea que esta fórmula se atribuye con razón a Pitágoras personalmente, [...] uno puede asumir con seguridad que pertenece al período muy antigua de las matemáticas pitagóricas."
Alrededor de 400 aC, según Proclo, Platón dio un método para encontrar ternas pitagóricas que combinaba el álgebra y la geometría. Alrededor de 300 aC, en la de Euclides elementos , la más antigua que existe prueba axiomática se presenta del teorema.
En la cultura popular
El teorema de Pitágoras ha surgido enla cultura popularen una variedad de maneras.
- Un verso de lacanción de mayor general en elGilbert y Sullivan ópera cómica The Pirates of Penzance"Acerca teorema del binomio que estoy lleno de un montón o 'noticias, Con muchos hechos alegres sobre el cuadrado de la hipotenusa", hace un oblicuo referencia al teorema.
- La Espantapájaros en la película El Mago de Oz hace una referencia más específica al teorema. Al recibir su diploma de la Asistente, inmediatamente se exhibe su "conocimiento" recitando una versión mutilada e incorrecta del teorema: "La suma de las raíces cuadradas de dos lados de un triángulo isósceles es igual a la raíz cuadrada de la restante lado. Oh, alegría! ¡Oh, éxtasis! Tengo un cerebro! "
- En 2000, Uganda lanzó una moneda con la forma de un triángulo rectángulo isósceles. La cola de la moneda tiene una imagen de Pitágoras y la ecuación α 2 + β 2 = γ 2 , acompañado con la mención "Pitágoras Milenio".
 | |
- Grecia,Japón,San Marino,Sierra LeonaySurinamehan emitidosellos postalesque representan Pitágoras y el teorema de Pitágoras.
- En Ficción especulativa de Neal Stephenson Anathem , el teorema de Pitágoras se conoce como 'el teorema Adrakhonic'. Una prueba geométrica del teorema se muestra en el lado de una nave alienígena para demostrar la comprensión de los alienígenas de las matemáticas.
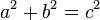
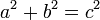
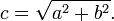
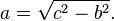
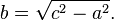
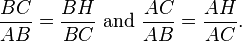
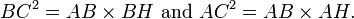
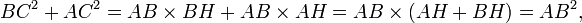
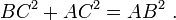
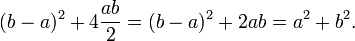
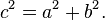
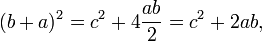
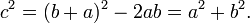
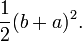
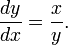
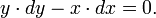
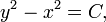
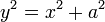
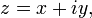
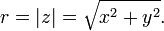
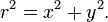
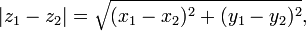
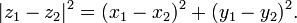
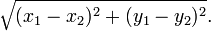
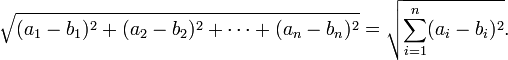
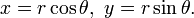
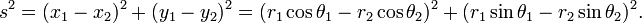
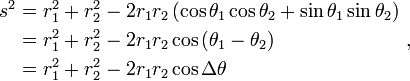

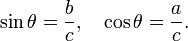
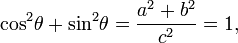

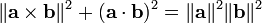
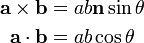
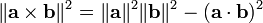
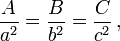
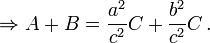

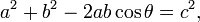

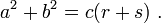
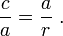
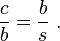
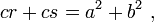


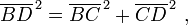
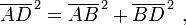
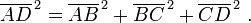
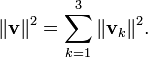

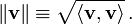
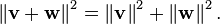
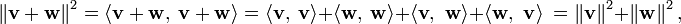
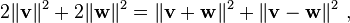
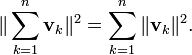
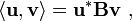
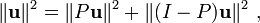
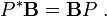
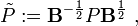

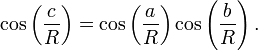
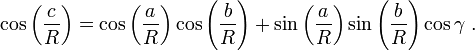
![1-\left(\frac{c}{R}\right)^2= \left[1-\left(\frac{a}{R}\right)^2 \right]\left[1-\left(\frac{b}{R}\right)^2 \right] + \ \mathrm{higher\ order\ terms}](../../images/1436/143667.png)