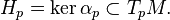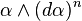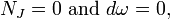Geometría diferencial
Acerca de este escuelas selección Wikipedia
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?
Geometría diferencial es un matemático disciplina que utiliza los métodos de diferencial e integral de cálculo para el estudio de problemas de geometría . La teoría del plano y el espacio curvas y de superficies en las tres dimensiones del espacio euclidiano sirvieron de base para su desarrollo inicial en el siglo XVIII y XIX. Desde finales del siglo XIX, la geometría diferencial se ha convertido en un campo de que se trate de manera más general con estructuras geométricas en variedades diferenciables. Está estrechamente relacionado con topología diferencial y con los aspectos geométricos de la teoría de ecuaciones diferenciales . La prueba de la Conjetura de Poincaré utilizando las técnicas de Flujo de Ricci demostró el poder del enfoque diferencial geométrica a las preguntas en la topología y destacó el importante papel desempeñado por los métodos analíticos.
Las ramas de la geometría diferencial
La geometría de Riemann
Estudios de la geometría de Riemann Variedades de Riemann, múltiples lisos con una métrica de Riemann, una noción de distancia expresada por medio de una definida positiva forma bilineal simétrica definida en el espacio tangente en cada punto. La geometría de Riemann generaliza la geometría euclidiana a espacios que no son necesariamente plana, aunque todavía se parecen al espacio euclidiano en cada punto "infinitesimal", es decir, en el primer orden de aproximación. Varios conceptos basados en longitud, como el longitud de arco de curvas , área de regiones planas, y el volumen de sólidos de todos los análogos naturales admiten en la geometría de Riemann. La noción de una derivada direccional de una función de la cálculo multivariable se extiende en la geometría de Riemann a la noción de un derivada covariante de un tensor. Muchos de los conceptos y técnicas de análisis y ecuaciones diferenciales se han generalizado a la fijación de las variedades de Riemann.
Una distancia de preservación difeomorfismo entre variedades de Riemann se llama isometría. Esta noción también se puede definir localmente, es decir, para pequeños barrios de puntos. Cualquiera de las dos curvas regulares son localmente isométrica. Sin embargo, Teorema Egregium de Gauss mostró que ya para superficies, la existencia de una isometría locales impone fuertes condiciones de compatibilidad en sus mediciones: la Curvaturas de Gauss en los puntos correspondientes deben ser las mismas. En dimensiones más altas, la Tensor de curvatura es un importante invariante puntual asociada a una variedad de Riemann que mide lo cerca que está de ser plana. Una clase importante de variedades de Riemann está formado por la Espacios simétricos de Riemann, cuya curvatura es constante. Son el más cercano al plano de "ordinario" y el espacio considerado en euclidiana y geometría no euclidiana.
Geometría pseudo-riemanniana
Geometría pseudo-riemanniana generaliza la geometría de Riemann para el caso en que el tensor métrico no tiene que ser definida positiva. Un caso especial de esto es una Colector de Lorentz, que es la base matemática de Einstein teoría de la relatividad general de gravedad .
Geometría Finsler
Geometría Finsler tiene el colector Finsler como el principal objeto de estudio - esto es una variedad diferencial con un Finsler métrica, es decir, un Banach norma definida en cada espacio tangente. Una métrica Finsler es una estructura mucho más general que una métrica de Riemann. Una estructura Finsler en un colector de M es una función F: T M → [0, ∞) tal que:
- F (x, mi) = mF (x, y) para todas las x, y en T M,
- F es infinitamente diferenciable en T M - {0},
- La Arpillera vertical de F 2 es definida positiva.
Geometría simpléctica
Simpléctica geometría es el estudio de colectores simplécticos. Un colector de casi simpléctica es una variedad diferenciable equipada con un suavemente variable no degenerado antisimétrica forma bilineal en cada espacio tangente, es decir, un no degenerada 2- forma ω, llamada la forma simpléctica. Una variedad simpléctica es una variedad casi simpléctica para el que se cierra la forma ω simpléctica: d ω = 0.
La difeomorfismo entre dos colectores simplécticos que conserva la forma simpléctica se llama symplectomorphism. No degenerado antisimétrica formas bilineales sólo pueden existir incluso en espacios vectoriales bidimensionales, así colectores simplécticos tienen necesariamente incluso dimensión. En la dimensión 2, una variedad simpléctica es sólo una superficie dotada de una forma de área y un symplectomorphism es un difeomorfismo área de preservación. La espacio de fase de un sistema mecánico es una variedad simpléctica y que hizo una aparición implícita ya en la obra de Lagrange en mecánica analítica y más tarde en Jacobi y Hamilton de formulación de la mecánica clásica.
En contraste con la geometría de Riemann, donde el curvatura proporciona una invariante locales de variedades de Riemann, El teorema de Darboux establece que todos los colectores simplécticos son localmente isomorfos. Los únicos invariantes de una variedad simpléctica son de naturaleza global y aspectos topológicos juegan un papel destacado en la geometría simpléctica. El primer resultado de la topología simpléctica es probablemente el Poincaré-Birkhoff teorema, conjeturado por Henri Poincaré y probado por George Birkhoff en 1912. Se afirma que si un área preservar mapa de un giros de corona circular cada componente límite en direcciones opuestas, a continuación, el mapa tiene al menos dos puntos fijos.
Contacto geometría
Póngase en contacto con la geometría trata con ciertas variedades de dimensión impar. Está cerca de la geometría simpléctica y como este último, que se originó en las preguntas de la mecánica clásica. Una estructura de contacto en un (2n + 1) dimensional variedad M está dada por una suave H campo hiperplano en el fibrado tangente que es lo más lejos posible de ser asociado con los conjuntos de nivel de una función diferenciable en M (el término técnico es "distribución hiperplano tangente completamente no integrables"). Cerca de cada punto p, una distribución hiperplano está determinada por una fuga en ninguna parte 1-forma 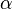 , Que es único hasta la multiplicación por una función de ninguna parte de fuga:
, Que es único hasta la multiplicación por una función de ninguna parte de fuga:
A 1-forma local el M es un formulario de contacto si la restricción de su derivada exterior de H es una 2-forma no degenerada y por lo tanto induce una estructura simpléctica en H p en cada punto. Si la distribución de H puede ser definido por una 1-forma mundial 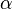 entonces esta forma es el contacto si y sólo si la forma-top dimensional
entonces esta forma es el contacto si y sólo si la forma-top dimensional
es un forma volumen en M, es decir, no se anula en cualquier lugar. Un análogo de contacto del teorema de Darboux sostiene: todas las estructuras de contacto en un colector y pico dimensiones son localmente isomorfo y pueden ser llevados a una cierta forma normal local mediante una elección adecuada del sistema de coordenadas.
Complejo y geometría Kähler
Geometría diferencial Complejo es el estudio de variedades complejas. Una colector casi compleja es una variedad de bienes 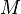 , Dotado de una tensor de tipo (1,1), es decir, una endomorphism fibrado vectorial (llamado estructura casi compleja)
, Dotado de una tensor de tipo (1,1), es decir, una endomorphism fibrado vectorial (llamado estructura casi compleja)
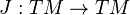 , De tal manera que
, De tal manera que 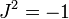 .
.
Se desprende de esta definición que un colector de casi compleja es aún dimensional.
Un colector de casi complejo se denomina complejo si 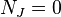 , Donde
, Donde 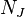 es un tensor de tipo (2,1) en relación con
es un tensor de tipo (2,1) en relación con 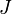 , Llamado Nijenhuis tensor (o algunas veces la torsión). Un colector de casi complejo es compleja si y sólo si admite una holomorfa coordinar atlas. Una estructura casi hermitiana está dada por una estructura casi compleja J, junto con una g métrica riemanniana, que satisface la condición de compatibilidad
, Llamado Nijenhuis tensor (o algunas veces la torsión). Un colector de casi complejo es compleja si y sólo si admite una holomorfa coordinar atlas. Una estructura casi hermitiana está dada por una estructura casi compleja J, junto con una g métrica riemanniana, que satisface la condición de compatibilidad 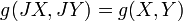 . Una estructura casi hermitiano define naturalmente diferencial 2-forma
. Una estructura casi hermitiano define naturalmente diferencial 2-forma 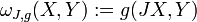 . Las dos condiciones siguientes son equivalentes:
. Las dos condiciones siguientes son equivalentes:
donde  es el Conexión de Levi-Civita de
es el Conexión de Levi-Civita de 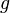 . En este caso,
. En este caso, 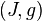 se denomina una Kähler estructura, y un colector de Kähler es un colector dotado de una estructura Kähler. En particular, un colector de Kähler es a la vez un complejo y una variedad simpléctica. Una gran clase de variedades de Kähler (la clase de Colectores Hodge) viene dada por todo el buen variedades proyectivas complejas.
se denomina una Kähler estructura, y un colector de Kähler es un colector dotado de una estructura Kähler. En particular, un colector de Kähler es a la vez un complejo y una variedad simpléctica. Una gran clase de variedades de Kähler (la clase de Colectores Hodge) viene dada por todo el buen variedades proyectivas complejas.
Geometría CR
Geometría CR es el estudio de la geometría intrínseca de límites de los dominios en variedades complejas.
Paquetes y conexiones
El aparato de la paquetes del vector, fibrados principales, y conexiones en ellas juega un papel extraordinariamente importante en la geometría diferencial moderna. Un colector de curva siempre lleva un paquete del vector natural, la paquete de la tangente. En términos generales, esta estructura por sí misma es suficiente sólo para el desarrollo de análisis en el colector, mientras que hace la geometría requiere además alguna manera para relacionar los espacios tangentes en diferentes puntos, es decir, una noción de transporte paralelo. Un ejemplo importante es proporcionado por conexiones afines. Para superficie en R 3, planos tangentes en diferentes puntos puede ser identificado usando la naturaleza plana del espacio euclidiano ambiente. En La geometría de Riemann, la Conexión de Levi-Civita sirve a un propósito similar. Más en general, geómetras diferenciales consideran espacios con un haz vector y una conexión como un reemplazo para la noción de una Variedad de Riemann. En este enfoque, el haz es externo al colector y tiene que ser especificado como parte de la estructura, mientras que la conexión proporciona una mejora adicional. En física, el colector puede ser el espacio-tiempo y haces y conexiones corresponden a diversos campos físicos.
Intrínseca frente extrínseca
Inicialmente y hasta mediados del siglo XIX , la geometría diferencial fue estudiada desde el punto de vista extrínseco: curvas y superficies fueron considerados como acostado en un espacio euclídeo de dimensión superior (por ejemplo una superficie en una espacio de tres dimensiones del ambiente). Los resultados más simples son los de la la geometría diferencial de curvas. A partir de la obra de Riemann , el punto de vista intrínseco se desarrolló, en el que no se puede hablar de mover el objeto geométrico "fuera" ya que se considera como dado de manera independiente.
El punto de vista intrínseco es más flexible. Por ejemplo, es útil en la relatividad donde el espacio-tiempo no puede, naturalmente, ser tomado como extrínseca (lo que sería "fuera" de ella?). Con el punto de vista intrínseco es más difícil definir el concepto central de curvatura y otras estructuras tales como conexiones, por lo que hay un precio que pagar.
Estos dos puntos de vista se pueden conciliar, es decir, la geometría extrínseca puede ser considerado como una estructura adicional a la intrínseca. (Véase el Nash incrustar teorema.)
Aplicaciones de la geometría diferencial
A continuación se presentan algunos ejemplos de cómo la geometría diferencial se aplica a otros campos de la ciencia y las matemáticas.
- En la física , la geometría diferencial es el idioma en el que Einstein la teoría general de la relatividad se expresa. Según la teoría, el universo es una variedad diferenciable equipada con métrica pseudo-riemanniana, que describió la curvatura de espacio tiempo. La comprensión de esta curvatura es esencial para el posicionamiento de satélites en órbita alrededor de la tierra. Geometría diferencial también es indispensable en el estudio de lentes gravitacionales y los agujeros negros .
- En economía , la geometría diferencial tiene aplicaciones en el campo de la econometría.
- Modelado geométrico (incluyendo gráficos por ordenador) y asistido por ordenador diseño geométrico empate en las ideas de la geometría diferencial.
- En ingeniería , geometría diferencial puede aplicarse para resolver problemas en procesamiento de la señal digital.
- En la física , el uso de formas diferenciales es útil en el estudio de electromagnetismo .
- En la física , la geometría diferencial tiene aplicaciones tanto para Mecánica lagrangiana y Mecánica hamiltoniana. Colectores simplécticos en particular, pueden ser utilizados para estudiar Sistemas hamiltonianos.