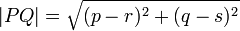Geometría euclidiana

Una representación de Euclides de La Escuela de Atenas de Rafael .

La geometría euclidiana es un sistema matemático atribuido a la Griego matemático Euclides de Alejandría . Texto de Euclides Elementos es la discusión sistemática conocido más antiguo de la geometría . Ha sido uno de los libros más influyentes de la historia, tanto por su método como por su contenido matemático. El método consiste en asumir un pequeño conjunto de intuitivamente atractiva axiomas y luego probando muchos otros proposiciones ( teoremas ) de esos axiomas. Aunque muchos de los resultados de Euclides había sido declarado por los matemáticos griegos anteriores, Euclides fue el primero en mostrar cómo estas proposiciones podrían encajan en una deductivo integral y sistema lógico.

Los Elementos comienzan con la geometría plana , todavía se enseña en la escuela secundaria como el primer sistema axiomático y los primeros ejemplos de la prueba formal . The Elements pasa a la geometría sólida de tres dimensiones y la geometría euclidiana se extendió posteriormente a cualquier número finito de dimensiones. Gran parte de los elementos de los estados resultados de lo que ahora se llama la teoría de números , demostrado mediante métodos geométricos.

Durante más de dos mil años, el adjetivo "euclidiana" era innecesaria porque ningún otro tipo de geometría había sido concebido. Axiomas de Euclides parecían tan intuitivamente obvio que cualquier teorema demostrado de ellos se consideró cierto en un sentido absoluto. Hoy, sin embargo, muchas otras auto-consistente geometrías no euclidianas son conocidos, los primeros en haber sido descubiertos en el siglo 19. También ya no se da por sentado que la geometría euclidiana describe el espacio físico. Una implicación de Einstein teoría de la 's la relatividad general es que la geometría euclidiana es sólo una buena aproximación a las propiedades del espacio físico si el campo gravitatorio no es demasiado fuerte.

Enfoque axiomático

La geometría euclidiana es un sistema axiomático, en el que todos los teoremas ("declaraciones verdaderas") se derivan de un número finito de axiomas. Cerca del principio del primer libro de los Elementos, de Euclides da cinco postulados (axiomas):

1. Cualquiera de los dos puntos pueden estar unidos por una línea recta .
2. Cualquier segmento de línea recta se puede extender indefinidamente en una línea recta.
3. Dado cualquier segmento de línea recta, un círculo se puede dibujar el segmento que tiene como radio y un punto final como el centro.
4. Todos ángulos rectos son congruentes.
5. Postulado de las paralelas. Si se cruzan dos líneas tercio de tal manera que la suma de los ángulos interiores de un lado es menor que dos ángulos rectos, entonces las dos líneas inevitablemente deben cruzarse entre sí en ese lado si se extiende lo suficientemente lejos.

Estos axiomas invocan los siguientes conceptos: punto, segmento de línea recta y la línea, lado de una línea, un círculo con radio y el centro, en ángulo recto, la congruencia, ángulos interiores y derecha, suma. Los siguientes verbos aparecen: unir, extender, dibujar, se cruzan. El círculo descrito en el postulado 3 es tácitamente único. Postulados 3 y 5 mantienen sólo para la geometría plana; en tres dimensiones, postulado 3 define una esfera.

Una prueba de los elementos de Euclides que, dado un segmento de línea, existe un triángulo equilátero que incluye el segmento como uno de sus lados. La prueba es por la construcción: un triángulo equilátero ΑΒΓ se hace dibujando círculos Δ y Ε centradas en los puntos Α y Β, y teniendo una intersección de los círculos como el tercer vértice del triángulo.

Postulado 5 conduce a la misma geometría que la siguiente declaración, conocida como Axioma de Playfair, que también lleva a cabo sólo en el plano:

A través de un punto no en una línea recta dada, una y sólo una línea puede ser dibujado que nunca se reúne la línea dada.

Postulados 1, 2, 3, 5 y afirmar la existencia y unicidad de ciertas figuras geométricas, y estas afirmaciones son de carácter constructivo: es decir, que no sólo se nos dice que existen ciertas cosas, pero también se dan los métodos para la creación de ellos con no más de un compás y una regla no marcado . En este sentido, la geometría euclidiana es más concreto que muchos sistemas axiomáticos modernas como la teoría de conjuntos , que a menudo afirman la existencia de los objetos sin decir cómo construir ellos, o incluso afirmar la existencia de objetos que no se pueden construir dentro de la teoría.

En rigor, las construcciones de líneas sobre el papel, etc son modelos de los objetos definidos en el sistema formal, en lugar de las instancias de los objetos. Por ejemplo, una línea recta euclídea no tiene anchura, pero cualquier recta real sorteados.

Los elementos también incluye los siguientes cinco "nociones comunes":

1. Las cosas que son iguales a la misma cosa también son iguales entre sí.
2. Si se añaden iguales a iguales, entonces los conjuntos son iguales.
3. Si los iguales se restan de iguales, entonces los restos son iguales.
4. Cosas que coinciden entre sí son iguales entre sí.
5. El todo es mayor que la parte.

Euclides también invocó otras propiedades pertenecientes a magnitudes. 1 es la única parte de la lógica subyacente que Euclides articulado de forma explícita. 2 y 3 son principios "aritméticos"; tenga en cuenta que se tienen los significados de "añadir" y "restar" en este contexto puramente geométrica como dado. 1 a 4 definen operacionalmente igualdad, que también puede ser tomado como parte de la lógica subyacente o como una relación de equivalencia que requiere, al igual que "coincide", definición previa cuidadosa. 5 es un principio de mereología. "Todo", "parte" y "resto" pedir definiciones precisas.

En el siglo 19, se dio cuenta de que diez axiomas de Euclides y nociones comunes no son suficientes para demostrar todos los teoremas enunciados en los Elementos. Por ejemplo, Euclides asume implícitamente que cualquier línea contiene al menos dos puntos, pero esta hipótesis no puede ser probada por los otros axiomas, y por lo tanto tiene que ser un axioma en sí. La primera prueba geométrica en los Elementos, que se muestra en la figura de la derecha, es que cualquier segmento de línea es parte de un triángulo; Euclides construye esto en la forma habitual, dibujando círculos alrededor de los dos puntos finales y teniendo su intersección como el tercer vértice. Sus axiomas, sin embargo, no garantizan que los círculos en realidad se cruzan, porque son consistentes con discreta, en lugar de continua, el espacio. Empezando con Moritz Pasch en 1882, se han propuesto muchos sistemas axiomáticos mejorados para la geometría, el más conocido es las de Hilbert, George Birkhoff, y Tarski.

Para ser justos con Euclides, el primero lógica formal capaz de soportar su geometría era la de Frege 1879 Begriffsschrift, poco leído hasta la década de 1950. Ahora vemos que la geometría euclidiana debe formar parte de la lógica de primer orden con identidad, un sistema formal primera figura en Hilbert y Wilhelm Ackermann del 1928 Principios de lógica teórica. Formal mereología no comenzó hasta 1916, con la obra de Lesniewski y AN Whitehead. Tarski y sus estudiantes hicieron un trabajo importante en el fundamentos de la geometría elemental tan recientemente como entre 1959 y su muerte en 1983.

El postulado de las paralelas

Para los antiguos, el postulado de las paralelas parecía menos evidente que los otros; verificando físicamente nos requeriría para inspeccionar dos líneas para comprobar que nunca se cruzaron, incluso en algún punto muy lejano, y esta inspección podría potencialmente tener una cantidad infinita de tiempo. El propio Euclides parece haber considerado como cualitativamente diferente de los demás, como lo demuestra la organización de los elementos: las primeras 28 proposiciones que presenta son las que se puede probar sin ella.

Muchos geómetras tratado en vano de demostrar el quinto postulado de los primeros cuatro. Por 1763, al menos 28 pruebas diferentes habían sido publicados, pero todo se descubra incorrecta. De hecho, el postulado de las paralelas no puede ser probada por los otros cuatro: esto se demostró en el siglo 19 por la construcción de alternativa ( no euclidiana) sistemas de geometría donde los otros axiomas están siendo cierto, pero el postulado de las paralelas es reemplazado por un axioma en conflicto. Un aspecto distintivo de estos sistemas es que los tres ángulos de un triángulo no suman 180 °: en la geometría hiperbólica la suma de los tres ángulos es siempre menor que 180 ° y puede aproximarse a cero, mientras que en la geometría elíptica es mayor que 180 °. Si el postulado de las paralelas se cae de la lista de axiomas sin reemplazo, el resultado es la geometría más general llamado geometría absoluta.

El tratamiento con la geometría analítica

El desarrollo de la geometría analítica proporciona un método alternativo para la formalización de la geometría. En este enfoque, un punto está representado por su cartesianas (x, y) de coordenadas, una línea está representada por su ecuación, y así sucesivamente. En el siglo 20, este ajuste en David Hilbert programa de reducción de todas las matemáticas a la aritmética, y luego probar la consistencia de la aritmética usando razonamiento finitistic 's. En enfoque original de Euclides, el teorema de Pitágoras se sigue de los axiomas de Euclides. En el enfoque cartesiano, los axiomas son los axiomas del álgebra, y la ecuación que expresa el teorema de Pitágoras es entonces una definición de uno de los términos en los axiomas de Euclides, que ahora se consideran teoremas. La ecuación

la definición de la distancia entre dos puntos 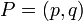y 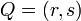se conoce entonces como la euclidiana métrica, y otras métricas definen geometrías no euclidianas.

Como descripción de la realidad física

Una refutación de la geometría euclidiana como una descripción del espacio físico. En un ensayo de 1919 de la teoría general de la relatividad, las estrellas (marcado con líneas horizontales cortas) fueron fotografiados durante un solar Eclipse. Los rayos de luz de las estrellas se inclinaban por la gravedad del Sol en su camino hacia la tierra. Esto se interpreta como evidencia a favor de la predicción de Einstein que la gravedad haría que las desviaciones de la geometría euclidiana.

Euclides creía que sus axiomas eran declaraciones evidentes sobre la realidad física.

Esto dio lugar a profundas dificultades filosóficas en la conciliación de la situación de los conocimientos de la observación en lugar de conocimientos adquiridos por la acción del pensamiento y el razonamiento. Una importante investigación de esta área fue realizada por Immanuel Kant en La Crítica de la razón pura.

Sin embargo, de Einstein teoría de la relatividad general demuestra que la verdadera geometría del espacio-tiempo es geometría no euclidiana. Por ejemplo, si un triángulo está compuesto de tres rayos de luz, entonces, en general, los ángulos interiores no suman 180 grados debido a la gravedad. Un campo gravitatorio relativamente débil, tal como la de la Tierra o el sol de, está representado por una métrica que es de aproximadamente, pero no exactamente, euclidiana. Hasta el siglo 20, no había la tecnología capaz de detectar las desviaciones de la geometría euclidiana, pero Einstein predijo que existirían tales desviaciones. Posteriormente fueron verificados por observaciones como la observación de la ligera curvatura de la luz de las estrellas por el Sol durante un eclipse solar en 1919, y geometría no euclidiana es ahora, por ejemplo, una parte integral de software que se ejecuta el Sistema GPS. Es posible oponerse a la interpretación no euclidiana de la relatividad general en razón de que los rayos de luz pueden ser modelos físicos inadecuados de líneas de Euclides, o que la relatividad podrían reformularse a fin de evitar las interpretaciones geométricas. Sin embargo, una de las consecuencias de la teoría de Einstein es que no hay ninguna posible prueba física que puede hacer nada mejor que un rayo de luz como un modelo de la geometría. Por lo tanto, las únicas posibilidades lógicas son a aceptar geometría no euclidiana como físicamente real, o de rechazar toda la noción de pruebas físicas de los axiomas de la geometría, que luego se pueden imaginar como un sistema formal sin ningún significado intrínseco en el mundo real.

Debido a la incompatibilidad del Modelo Estándar de la relatividad general , y debido a algún reciente evidencia empírica en contra de la primera, ambas teorías están ahora bajo un mayor escrutinio, y se han propuesto muchas teorías para sustituir a la antigua y, en muchos casos, este último como también. ( GUT son el único ejemplo de las teorías de modelos post-estándar que no aborda la relatividad general.) Los desacuerdos entre las dos teorías provienen de sus afirmaciones acerca de espacio-tiempo, y ahora se acepta que la geometría física debe describir el espacio-tiempo en lugar de simplemente el espacio. Mientras que la geometría euclidiana, el Modelo Estándar y la relatividad general son todos compatibles con cualquier número de dimensiones espaciales y cualquier especificación sobre cuál de estos si alguno está compactificada (ver la teoría de cuerdas ), y mientras toda la geometría euclidiana bar (que no distingue el espacio de tiempo) insisten en exactamente una dimensión temporal, las alternativas propuestas, ninguna de las cuales todavía son parte de consenso científico, difieren significativamente en sus predicciones o falta de ella en cuanto a estos detalles del espacio-tiempo. Los desacuerdos entre la teorías preocupación física convencional si el espacio-tiempo es euclidiana (desde la teoría cuántica de campos en el modelo estándar se basa en la suposición de que es) y de si se trata cuantizada. Pocos o ningún alternativas propuestas niegan que el espacio-tiempo se cuantifica, con la quanta de la longitud y el tiempo son, respectivamente, la Longitud de Planck y la Tiempo de Planck. Sin embargo, lo que la geometría de usar - euclidiana, Riemann, de Stitter, anti de Stitter y algunos otros - es un importante punto de demarcación entre ellos. Muchos físicos esperan que algunos la teoría de cuerdas de Euclides para convertirse eventualmente en la Teoría del Todo, pero su opinión es de ninguna manera unánime, y en cualquier caso, el futuro de este tema es impredecible. En cuanto a la forma en todo caso la geometría euclidiana estarán involucrados en la física futuro, lo que es indiscutible es que la definición de líneas rectas todavía estará en función de la ruta en el vacío de la radiación electromagnética (luz incluida) hasta que la gravedad se explica con coherencia matemática en términos de un fenómeno distinto de la curvatura del espacio-tiempo, y que la prueba de postulados geométricos (euclidianas o no) estará en el estudio de cómo estos caminos se ven afectados por fenómenos. Por ahora, la gravedad es el fenómeno relevante sólo conocida, y su efecto es controvertido (ver lente gravitacional).

Las secciones cónicas y teoría gravitacional

Apolonio y otros geómetras griegos antiguos hicieron un extenso estudio de las secciones cónicas - Curvas creados por la intersección de un cono y un plano. Los (no degeneradas) cuáles son los elipse , la parábola y la hipérbola, se distinguió por tener cero, uno o dos intersecciones con el infinito. Esto resultó para facilitar el trabajo de Galileo , Kepler y Newton en el siglo 17, ya que estas curvas modelados con precisión el movimiento de los cuerpos bajo la influencia de la gravedad. Uso La ley de la gravitación universal de Newton, la órbita de un cometa alrededor del Sol es

• una elipse, si se está moviendo demasiado lentamente para su posición (por debajo velocidad de escape), en cuyo caso se volverá eventual;
• una parábola, si se está moviendo con velocidad de escape exacta (poco probable), y nunca volverá porque la curva alcanza hasta el infinito; o
• una hipérbola, si se está moviendo lo suficientemente rápido (por encima de la velocidad de escape), y del mismo modo jamás volver.

En cada caso, el Sol estará en uno foco de la cónica, y el movimiento barrerá áreas iguales en tiempos iguales.

Galileo experimentó con la caída de objetos distancias pequeñas en la superficie de la Tierra, y empíricamente determinado que la distancia recorrida era proporcional al cuadrado del tiempo. Dada su aparato de cronometraje y medición, esto era una excelente aproximación. Durante distancias tan pequeñas que la aceleración de la gravedad puede considerarse constante, y haciendo caso omiso de los efectos de aire (como en una pluma que cae) y la rotación de la Tierra , los trayectoria de una proyectil será una trayectoria parabólica.

Cálculos posteriores de estos caminos para los cuerpos en movimiento por gravedad se realizaron utilizando las técnicas de la geometría analítica (usando coordenadas y álgebra) y el cálculo diferencial, que proporcionan pruebas directas. Por supuesto, estas técnicas no se habían inventado en el momento en que Galileo investigó el movimiento de caída de los cuerpos. Una vez que se encontró con que los cuerpos caen a la Tierra con una aceleración constante (dentro de la precisión de sus métodos), demostró que los proyectiles se moverán en una trayectoria parabólica utilizando los procedimientos de la geometría euclidiana.

Del mismo modo, Newton utilizó cuasi-euclidianas pruebas para demostrar la derivación de los movimientos orbitales de Kepler de sus leyes del movimiento y la gravitación.

Siglos más tarde, una de las primeras medidas experimentales para apoyar Einstein 's teoría general de la relatividad , que postula un geometría no euclidiana para el espacio, fue la órbita del planeta Mercurio . Kepler describe la órbita como una elipse perfecta. La teoría de Newton predijo que la influencia gravitatoria de otros órganos daría una órbita más complicado. Pero con el tiempo todas esas correcciones newtoniana estuvieron a la altura de los resultados experimentales; una pequeña perturbación se mantuvo. Einstein postuló que la curvatura del espacio explicaría precisamente por esa perturbación.

Estado lógico

La geometría euclidiana es una teoría de primer orden . Es decir, permite que declaraciones como las que comienzan como "para todos los triángulos ...", pero es incapaz de formar frases como "para todos los conjuntos de triángulos ...". Declaraciones de este último tipo se consideran fuera del ámbito de la teoría.

Le debemos mucho de nuestra actual comprensión de las propiedades de la lógica y propiedades metamatemáticos de la geometría euclidiana a la labor de Alfred Tarski y sus estudiantes, a partir de la década de 1920. Tarski demostró su formulación axiomática de la geometría euclidiana que se complete en un determinado sentido: hay un algoritmo que, para cada propuesta, se puede mostrar que sea verdadera o falsa. Teoremas de incompletitud de Gödel demostró la inutilidad de programa de la prueba de la consistencia de todas las matemáticas utilizando razonamiento finitistic de Hilbert. Resultados de Tarski no violan el teorema de Gödel, porque la geometría euclidiana no puede describir una cantidad suficiente de aritmética para el teorema de aplicar.

Aunque completa en la sentido formal utilizado en la lógica moderna, hay cosas que la geometría euclidiana no puede lograr. Por ejemplo, el problema de la trisección de un ángulo con un compás y una regla es uno que se produce naturalmente dentro de la teoría, puesto que los axiomas se refieren a operaciones constructivas que se pueden llevar a cabo con esas herramientas. Sin embargo, siglos de esfuerzos fallaron en encontrar una solución a este problema, hasta Pierre Wantzel publicó una demostración en 1837 que tal construcción era imposible.

Geometría absoluta, primero identificado por Bolyai, es la geometría euclidiana debilitado por omisión del quinto postulado, que las líneas paralelas no se encuentran. Por fuerza intermedia entre la geometría euclidiana son absoluta y geometrías derivadas de Euclides por alteraciones del postulado de las paralelas que se puede mostrar para ser consistente, al mostrar modelos de ellos. Por ejemplo, la geometría en la superficie de una esfera es un modelo de geometría elíptica. Otra debilidad de la geometría euclidiana es geometría afín, primero identificado por Euler , que conserva el quinto postulado no modificado mientras debilitamiento postula tres y cuatro en un modo que elimina las nociones de ángulo (de ahí triángulos rectángulos carecen de sentido) y de la igualdad de longitud de los segmentos de línea en general (círculos de donde se convierten sentido), manteniendo los conceptos de paralelismo como una relación de equivalencia entre líneas, y la igualdad de longitud de los segmentos de línea en paralelo (lo segmentos de línea siguen teniendo un punto medio).

Teoremas clásicos

• El teorema de Ceva
• La fórmula de Herón
• Circunferencia de los nueve puntos
• Teorema de pitágoras
• La fórmula de Tartaglia
• El teorema de Menelao
• Teorema de la bisectriz