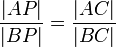Círculo
Antecedentes
Este contenido de Wikipedia ha sido seleccionada por SOS para su utilización en las escuelas de todo el mundo. Haga clic aquí para obtener información sobre el apadrinamiento de niños.
| Círculo | |
|---|---|
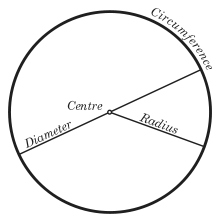 Ilustración Círculo mostrando un radio, un diámetro, el centro y la circunferencia | |
| Zona | 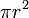 (Donde r = radio) (Donde r = radio) |

Un círculo es un simple forma de la geometría euclidiana que es el conjunto de todos puntos en un plano que son una distancia dada de un punto dado, la centro. La distancia entre cualquiera de los puntos y el centro se llama RADIUS. También se puede definir como el lugar geométrico de un punto equidistante desde un punto fijo.
Un círculo es una simple cerrada curva que divide el plano en dos regiones: una interior y un exterior. En el uso diario, el término "círculo" pueden utilizarse indistintamente para referirse a la frontera de la figura, o para toda la figura incluyendo su interior; en el uso técnico estricto, el círculo es el primero y el último se llama disco.
Un círculo se puede definir como la curva trazada por un punto que se mueve de manera que su distancia desde un punto dado es constante.
Un círculo también puede definirse como un especial elipse en la que los dos focos son coincidentes y la excentricidad es 0. Los círculos son secciones cónicas alcanzados cuando un cono circular recto está cortada por un plano perpendicular al eje del cono.
Terminología
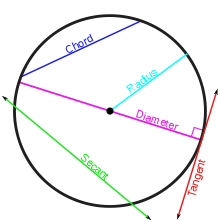
- Arco: cualquier parte conectada de la circunferencia del círculo.
- Centro: el punto equidistante de los puntos de la circunferencia.
- Acorde: un segmento de línea cuya puntos finales situados en el círculo.
- Circunferencia: la longitud de un circuito a lo largo del círculo.
- Diámetro : la cuerda más larga, un segmento de línea cuyos extremos situados en el círculo y que pasa por el centro; o la longitud de un segmento de este tipo, que es la mayor distancia entre dos puntos de la circunferencia.
- Radio: un segmento de línea que une el centro del círculo a cualquier punto en el círculo mismo; o la longitud de un segmento de este tipo, que es la mitad de un diámetro.
- Secante: un acorde extendida, una línea recta cortando el círculo en dos puntos.
- Sector: una región limitada por dos radios y un arco que se extiende entre los radios.
- Segmento: una región limitada por una cuerda y un arco que se extiende entre los extremos de la cuerda.
- Semicírculo: una región limitada por un diámetro y un arco que se extiende entre los puntos finales del diámetro. Se trata de un caso especial de un segmento.
- Tangente : una línea recta que toca el círculo en un solo punto.
 |
 |
Historia
La palabra "círculo" se deriva del griego, Kirkos "un círculo," desde el ker- base que significa girar o doblarse. Los orígenes de las palabras " circo "y" circuito "están estrechamente relacionados.

El círculo se conoce desde antes del comienzo de la historia registrada. Se han observado círculos naturales, tales como la Luna, el Sol, y un tallo de la planta corta soplando en el viento sobre la arena, que forma una forma de círculo en la arena. El círculo es la base de la rueda , que, con invenciones relacionadas, tales como engranajes, hace que gran parte de la maquinaria moderna posible. En matemáticas, el estudio del círculo ha ayudado a inspirar el desarrollo de la geometría, la astronomía , y cálculo.
Early la ciencia , en particular la geometría y la astrología y la astronomía, estaba conectado con lo divino para la mayoría eruditos medievales, y muchos creían que había algo intrínsecamente "divino" o "perfecto" que se podían encontrar en los círculos.
 La brújula en este manuscrito del siglo 13 es un símbolo del acto de Dios Creación. Nótese también la forma circular de la halo
La brújula en este manuscrito del siglo 13 es un símbolo del acto de Dios Creación. Nótese también la forma circular de la halo
 Togrul Torre desde el interior
Togrul Torre desde el interior
 Círculos en un viejo dibujo astronómico árabe
Círculos en un viejo dibujo astronómico árabe
Algunos aspectos destacados de la historia del círculo son:
- 1700 aC - El Rhind papiro da un método para calcular el área de un campo circular. El resultado corresponde a 256/81 (3,16049 ...) como un valor aproximado de π.
- 300 aC - Libro 3 de los Elementos de Euclides se ocupa de las propiedades de los círculos.
- En Platón 's Carta VII existe una definición detallada y explicación del círculo. Platón explica el círculo perfecto, y en qué se diferencia de cualquier dibujo, palabras, definición o explicación.
- 1880 CE- Lindemann prueba que π es trascendental, la solución efectiva al problema milenario de la cuadratura del círculo.
Resultados analíticos
Longitud de la circunferencia
La relación de un círculo de circunferencia a su diámetro es π (pi), un irracional constante aproximadamente igual a 3,141592654. Así, la longitud de la circunferencia C está relacionado con el radio R y el diámetro d por:
Área cerrada
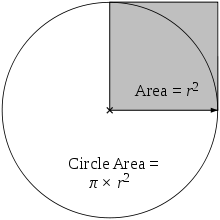
Como resultado de Arquímedes, el área encerrada por un círculo es igual a la de un triángulo cuya base tiene la longitud de la circunferencia del círculo y cuya altura es igual a el radio del círculo, que viene a π multiplicado por el radio al cuadrado:
De manera equivalente, denotando de diámetro por d,
es decir, aproximadamente el 79 por ciento de la cuadrado circunscrito (cuyo lado es de longitud d).
El círculo es la curva plana que encierra el área máxima para una longitud de arco dado. Esto se refiere el círculo a un problema en el cálculo de variaciones , a saber, la Isoperimetría.
Ecuaciones
Coordenadas cartesianas

En una x - y sistema de coordenadas cartesianas , el círculo con centro coordenadas (a, b) y radio r es el conjunto de todos los puntos (x, y) tales que
Esta ecuación , también conocida como ecuación de la circunferencia, sigue desde el teorema de Pitágoras aplicado a cualquier punto en el círculo: como se muestra en el diagrama de la derecha, el radio es la hipotenusa de un triángulo rectángulo cuyos otros lados son de longitud x - a e y - b. Si el círculo está centrado en el origen (0, 0), entonces la ecuación se simplifica a
La ecuación puede ser escrita en forma paramétrica utilizando la funciones trigonométricas seno y coseno como
donde t es una la variable paramétrica en el rango de 0 a 2π, interpretarse geométricamente como el ángulo que el rayo de (a, b) a (x, y) forma con el eje x. Una parametrización alternativa del círculo es:
En esta parametrización, la proporción de t a r puede interpretarse geométricamente como la proyección estereográfica del círculo sobre la línea que pasa por el centro paralela a la eje x.
En coordenadas homogéneas cada sección cónica con la ecuación de un círculo es de la forma
Se puede demostrar que una sección cónica es un círculo exactamente cuando contiene (cuando se extiende a la complejo plano proyectivo) los puntos I (1: i: 0) y J (1: - i: 0). Estos puntos se denominan puntos circulares en el infinito.
Coordenadas polares
En coordenadas polares de la ecuación de un círculo es:
donde a es el radio del círculo, 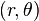 es la coordenada polar de un punto genérico en el círculo, y
es la coordenada polar de un punto genérico en el círculo, y 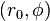 es el polo de coordenadas del centro del círculo (es decir, r 0 es la distancia desde el origen hasta el centro del círculo, y φ es el ángulo en sentido antihorario desde el eje x positivo x a la línea que conecta el origen hasta el centro de el círculo). Para un círculo centrado en el origen, es decir, r 0 = 0, esto reduce simplemente r = a. Cuando r 0 = a, o cuando el origen se encuentra en el círculo, la ecuación se convierte
es el polo de coordenadas del centro del círculo (es decir, r 0 es la distancia desde el origen hasta el centro del círculo, y φ es el ángulo en sentido antihorario desde el eje x positivo x a la línea que conecta el origen hasta el centro de el círculo). Para un círculo centrado en el origen, es decir, r 0 = 0, esto reduce simplemente r = a. Cuando r 0 = a, o cuando el origen se encuentra en el círculo, la ecuación se convierte
En el caso general, la ecuación puede resolverse para r, dando
la solución con un signo menos delante de la raíz cuadrada de dar la misma curva.
Plano complejo
En el plano complejo , un círculo con un centro en c y el radio (r) tiene la ecuación 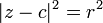 . En forma paramétrica esto se puede escribir
. En forma paramétrica esto se puede escribir 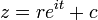 .
.
La ecuación ligeramente generalizada 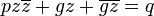 para p verdadero, q y g complejo a veces se llama un círculo generalizada. Esto se convierte en la ecuación anterior para un círculo con
para p verdadero, q y g complejo a veces se llama un círculo generalizada. Esto se convierte en la ecuación anterior para un círculo con 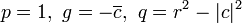 , Ya
, Ya 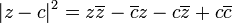 . No todos los círculos generalizadas son en realidad círculos: un círculo generalizada es o bien un (true) círculo o una línea .
. No todos los círculos generalizadas son en realidad círculos: un círculo generalizada es o bien un (true) círculo o una línea .
Líneas tangentes
La línea tangente a través de un punto P en el círculo es perpendicular al diámetro que pasa por P. Si P = (x 1, y 1) y el círculo tiene centro (a, b) y radio r, entonces la línea tangente es perpendicular a la línea de (a, b) a (x 1, y 1), por lo que tiene la forma (x 1 - a) x + (y 1 - b) = c. Evaluación en (x 1, y 1) determina el valor de c y el resultado es que la ecuación de la tangente es
o
Si y 1 ≠ B, entonces la pendiente de esta línea es
Esto también se puede encontrar utilizando diferenciación implícita.
Cuando el centro del círculo está en el origen entonces la ecuación de la recta tangente se vuelve
y su pendiente es
Propiedades
- El círculo es la forma con el área más grande para una determinada longitud de perímetro. (Ver Isoperimetría.)
- El círculo es una forma altamente simétrico: cada línea a través del centro forma una línea de simetría de reflexión y tiene simetría de rotación alrededor del centro para cada ángulo. Su grupo de simetría es el grupo ortogonal O (2, R). El grupo de rotaciones por sí sola es la grupo círculo T.
- Todos los círculos son similar.
- Circunferencia y el radio de un círculo son proporcional.
- El área encerrada por el cuadrado de su radio son proporcional.
- La constantes de proporcionalidad son 2π y π, respectivamente.
- El círculo que está centrado en el origen con radio 1 se llama el círculo unidad.
- Considerado como un gran círculo de la esfera unidad, se convierte en el Círculo de Riemann.
- A través de los tres puntos, no todos en la misma línea, se encuentra un círculo único. En coordenadas cartesianas , es posible dar fórmulas explícitas para las coordenadas del centro del círculo y el radio en términos de las coordenadas de los tres puntos dados. Ver circunferencia circunscrita.
Acorde
- Los acordes son equidistantes del centro de un círculo si y sólo si son iguales en longitud.
- La mediatriz de un acorde pasa a través del centro de un círculo; declaraciones equivalentes derivados de la singularidad de la mediatriz:
- Una línea perpendicular desde el centro de un círculo biseca el acorde.
- La segmento de línea ( segmento circular) a través del centro de bisección una cuerda es perpendicular a la cuerda.
- Si un ángulo central y una ángulo inscrito de un círculo se subtendido por el mismo acorde y en el mismo lado de la cuerda, entonces el ángulo central es el doble del ángulo inscrito.
- Si dos ángulos están inscritos en el mismo acorde y en el mismo lado de la cuerda, entonces son iguales.
- Si dos ángulos están inscritos en el mismo acorde y en lados opuestos de la cuerda, entonces son suplementarios.
- Para un cuadrilátero cíclico, el ángulo exterior es igual al ángulo opuesto interior.
- Un ángulo inscrito subtendido por un diámetro es un ángulo recto (ver Teorema de Tales).
- El diámetro es la cuerda más larga del círculo.
- Si la intersección de dos acordes divide un acorde en longitudes A y B y divide el otro acorde en longitudes c y d, entonces ab = cd.
- Si la intersección de dos acordes perpendiculares divide un acorde en longitudes A y B y divide el otro acorde en longitudes c y d, a continuación, un 2 + b 2 + c + d 2 2 es igual al cuadrado del diámetro.
- La suma de las longitudes de los cuadrados de las dos cuerdas se cortan en ángulos rectos en un punto dado es la misma que la de cualquier otro dos cuerdas se cortan en el mismo punto, y está dada por r 8 2 - 4 de p 2 (donde r es el radio y el p de círculo es la distancia desde el punto central hasta el punto de intersección).
- La distancia desde un punto en el círculo para un determinado acorde veces el diámetro del círculo es igual al producto de las distancias desde el punto a los extremos de la cuerda.
Sagitta

- El Sagitta (también conocido como el versine) es un segmento de línea dibujada perpendicular a una cuerda, entre el punto medio de ese acorde y el arco del círculo.
- Teniendo en cuenta la longitud y de un acorde, y la longitud x de la sagitta, el teorema de Pitágoras se puede utilizar para calcular el radio del círculo única que se ajuste alrededor de las dos líneas:
Otra prueba de este resultado que se basa sólo en dos propiedades acorde dado anteriormente es como sigue. Dada una cuerda de longitud y y con Sagitta de longitud x, ya que el Sagitta cruza por el medio de la cuerda, sabemos que es parte de un diámetro del círculo. Dado que el diámetro es dos veces el radio, la parte de "perdido" del diámetro es (2 r - x) de longitud. Usando el hecho de que una parte de uno de acordes veces la otra parte es igual al mismo producto tomada a lo largo de una cuerda que intersecta el primer acorde, nos encontramos con que (2 r - x) x = (y / 2) 2. Despejando r, encontramos el resultado requerido.
Tangente
- La línea dibujada perpendicular a un radio a través del punto final de la radio es una tangente al círculo.
- Una línea trazada perpendicular a una tangente a través del punto de contacto con un círculo pasa a través del centro del círculo.
- Dos tangentes siempre se pueden extraer a un círculo desde cualquier punto fuera del círculo, y estas tangentes son iguales en longitud.
- Si una tangente en A y una tangente en B se cruzan en el punto P exterior, a continuación, que denota el centro como O, los ángulos ∠ BOA y ∠ BPA son suplementaria.
- Si AD es tangente al círculo en A y si AQ es una cuerda de círculo, entonces ∠ DAQ = 1/2 arco (AQ).
Teoremas

- El teorema del acorde establece que si dos acordes, CD y EB, se cortan en A, entonces CA × DA = EA × BA.
- Si una tangente desde el punto D externa se encuentra con el círculo en C y un secante desde el punto D externa se encuentra con el círculo en G y E, respectivamente, entonces DC 2 = DG × DE. (Teorema-Tangente secante.)
- Si dos secantes, DG y DE, también cortar el círculo en H y F, respectivamente, entonces DH × DG = DF × DE. (Corolario del teorema tangente secante.)
- El ángulo entre la tangente y la cuerda es igual a la mitad del ángulo subtendido en el lado opuesto de la cuerda (Tangente de acordes de ángulo).
- Si el ángulo subtendido por la cuerda en el centro es 90 grados entonces L = r √2, donde l es la longitud de la cuerda y r es el radio del círculo.
- Si dos secantes se inscriben en el círculo, como se muestra a la derecha, entonces la medición del ángulo A es igual a una mitad de la diferencia de las mediciones de los arcos cerrados (DE y BC). Este es el teorema de la secante secante.
Ángulos inscritos

Una ángulo inscrito (ejemplos son los ángulos azul y verde en la figura) es exactamente la mitad de la correspondiente ángulo central (rojo). Por lo tanto, todos los ángulos inscritos que subtienden el mismo arco (rosa) son iguales. Ángulos inscritos en el arco (marrón) son suplementarios. En particular, cada ángulo inscrito que subtiende un diámetro es una ángulo recto (ya que el ángulo central es de 180 grados).
Círculo de Apolonio

Apolonio de Perga mostró que un círculo también puede definirse como el conjunto de puntos en un plano que tiene una relación constante (excepto 1) de las distancias a dos focos fijos, A y B. (El conjunto de puntos donde las distancias son iguales es la bisectriz perpendicular de A y B, una línea.) Ese círculo a veces se dice que está dibujado alrededor de dos puntos.
La prueba consta de dos partes. En primer lugar, hay que demostrar que, dados dos focos A y B y una relación de las distancias, cualquier punto P satisface la relación de distancias se debe caer en un círculo particular. Sea C otro punto, también la satisfacción de la relación y la mentira en el segmento AB. Por el Teorema de la bisectriz del PC segmento de línea bisectriz del interior ángulo APB, ya que los segmentos son similares:
Análogamente, un PD segmento de línea a través de algún punto D en AB extendido divide la correspondiente exterior ángulo BPQ donde Q es el AP extendido. Puesto que los ángulos interiores y exteriores suman 180 grados, el ángulo de CPD es exactamente 90 grados, es decir, una ángulo recto. El conjunto de puntos P de tal manera que CPD ángulo es un ángulo recto forma un círculo, de los cuales CD es un diámetro.
En segundo lugar, ver por una prueba de que cada punto en el círculo indicado satisface la relación dada.
Cross-ratios
Una propiedad estrechamente relacionado de círculos implica la geometría de la cross-proporción de puntos en el plano complejo . Si A, B y C son como anteriormente, entonces el círculo de Apolonio de estos tres puntos es el conjunto de puntos P para los que el valor absoluto de la razón doble es igual a uno:
Dicho de otra manera, P es un punto en el círculo de Apolonio si y sólo si la relación de cruz [A, B; C, P] está en el círculo unidad en el plano complejo.
Círculos generalizadas
Si C es el punto medio del segmento AB, entonces la colección de puntos P que satisface la condición Apolonio
no es un círculo, sino más bien una línea.
Por lo tanto, si A, B, y C se dan puntos distintos en el plano, entonces el lugar geométrico de puntos P que satisface la ecuación de arriba se llama un "círculo generalizada." Puede ser un verdadero círculo o una línea. En este sentido, una línea es un círculo generalizada de radio infinito.
Círculos inscritos en o circunscritas sobre otras figuras
En cada triángulo de un círculo único, llamado el incircle, puede ser inscrita de manera que es tangente a cada uno de los tres lados del triángulo.
Sobre todo triángulo un círculo único, llamado el circunferencia circunscrita, se puede circunscribir tal que pasa por cada uno de triángulo de tres vértices.
Un polígono tangencial, tal como una cuadrilátero tangencial, es cualquier polígono convexo dentro de un círculo que puede ser inscrito que es tangente a cada lado del polígono.
La polígono cíclico es cualquier polígono convexo sobre las que el círculo puede ser circunscrito, que pasa por cada vértice. Un ejemplo bien estudiado es el cuadrilátero cíclico.
La hipocicloide es una curva que se inscribe en un círculo dado trazando un punto fijo en un círculo más pequeño que rueda dentro y tangente a la circunferencia dada.
Círculo como caso límite de otras figuras
El círculo se puede ver como un caso límite de cada una de varias otras figuras:
- La Óvalo cartesiano es un conjunto de puntos de tal manera que una suma ponderada de las distancias desde cualquiera de sus puntos a dos puntos fijos ( focos) es una constante. Una elipse es el caso en el que los pesos son iguales. Un círculo es una elipse con una excentricidad de cero, lo que significa que los dos focos coinciden entre sí como el centro del círculo. Un círculo es también un caso especial diferente de un óvalo cartesiano en el que uno de los pesos es igual a cero.
- La superelipse tiene una ecuación de la forma
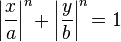 para los positivos a, b, y n. Un supercircle tiene b = a. Un círculo es el caso especial de un supercircle en la que n = 2.
para los positivos a, b, y n. Un supercircle tiene b = a. Un círculo es el caso especial de un supercircle en la que n = 2. - La Cassini ovalada es un conjunto de puntos tales que el producto de las distancias desde cualquiera de sus puntos a dos puntos fijos es una constante. Cuando los dos puntos fijos coinciden, un círculo resultados.
- La curva de anchura constante es una figura cuya anchura, que se define como la distancia perpendicular entre dos líneas paralelas diferentes, cada uno de intersección su límite en un solo punto, es el mismo independientemente de la dirección de estas dos líneas paralelas. El círculo es el ejemplo más simple de este tipo de figura.
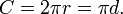
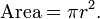
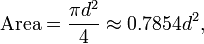
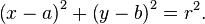
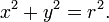
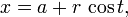
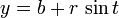
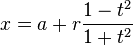
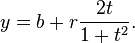
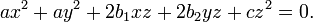
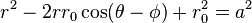
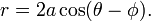
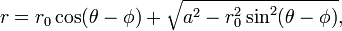
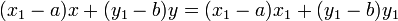
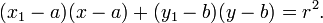
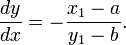
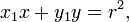
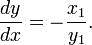
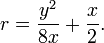
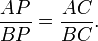
![| [A, B; C, P] | = 1. \](../../images/2039/203983.png)