
Serie de Taylor
Antecedentes
Organizar una selecci??n Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Una r??pida conexi??n para el apadrinamiento de ni??os es http://www.sponsor-a-child.org.uk/

 y las aproximaciones de Taylor, los polinomios de grado 1, 3, 5, 7, 9, 11 y 13.
y las aproximaciones de Taylor, los polinomios de grado 1, 3, 5, 7, 9, 11 y 13. 
En las matem??ticas , la serie de Taylor es una representaci??n de una funci??n como un infinito suma de t??rminos calculados a partir de los valores de sus derivados en un solo punto. Puede ser considerado como el l??mite de los polinomios de Taylor . Serie de Taylor se nombra en honor de Matem??tico Ingl??s Brook Taylor. Si la serie utiliza los derivados en cero, la serie tambi??n se denomina una serie de Maclaurin, nombrado despu??s Matem??tico escoc??s Colin Maclaurin.
Definici??n
La serie de Taylor de una verdadera o complejo de la funci??n f (x) que es infinitamente diferenciable en una barrio de un verdadero o complejo n??mero a, es la serie de potencias
que en una forma m??s compacta se puede escribir como
donde n! es el factorial de n y f (n) (a) denota el n-??simo derivado de f en el punto a; el derivado de cero de f se define como f s?? mismo y (x - a) 0 y 0! son a la vez definida que es 1.
A menudo, f (x) es igual a su serie de Taylor evaluado en x para todo x suficientemente cerca de a. Esta es la raz??n principal por la serie de Taylor son importantes.
En el caso particular donde  , La serie tambi??n se llama serie de Maclaurin.
, La serie tambi??n se llama serie de Maclaurin.
Ejemplos
La serie de Maclaurin para cualquier polinomio es el mismo polinomio.
La serie de Maclaurin para  es el serie geom??trica
es el serie geom??trica
por lo que la serie de Taylor de  en
en 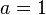 es
es
 .
.
Mediante la integraci??n de la anterior serie de Maclaurin encontramos la serie de Maclaurin para  , Donde
, Donde  denota el logaritmo natural :
denota el logaritmo natural :
y la serie de Taylor correspondiente para  en
en  es
es
 .
.
La serie de Maclaurin para la funci??n exponencial 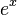 en
en  es
es
 .
.
La expansi??n precedente se mantiene porque la derivada de 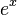 es tambi??n
es tambi??n 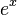 y
y  es igual a 1. Esto deja los t??rminos
es igual a 1. Esto deja los t??rminos  en el numerador y n! en el denominador para cada t??rmino de la suma infinita.
en el numerador y n! en el denominador para cada t??rmino de la suma infinita.
Convergencia

La serie de Taylor no tiene, en general, ser un serie convergente, pero a menudo es. El l??mite de una serie de Taylor convergente no tiene, en general, sea igual al valor de la funci??n f (x), pero a menudo es. Si f (x) es igual a su serie de Taylor en una vecindad de una, que se dice que es anal??tica en este barrio. Si f (x) es igual a su serie de Taylor en todas partes se llama entero. La funci??n exponencial 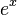 y la funciones trigonom??tricas seno y coseno son ejemplos de funciones enteras. Ejemplos de funciones que no son la totalidad incluyen el logaritmo , la funci??n trigonom??trica tangente, y su inversa arctan. Para estas funciones la serie de Taylor no lo hacen converger si x est?? lejos de a.
y la funciones trigonom??tricas seno y coseno son ejemplos de funciones enteras. Ejemplos de funciones que no son la totalidad incluyen el logaritmo , la funci??n trigonom??trica tangente, y su inversa arctan. Para estas funciones la serie de Taylor no lo hacen converger si x est?? lejos de a.
Una serie de Taylor se puede utilizar para calcular el valor de una funci??n entera en cada punto, si el valor de la funci??n, y de todos sus derivados, son conocidos en un solo punto. Usos de la serie de Taylor para funciones completas incluyen:
- Las sumas parciales (los polinomios de Taylor ) de la serie pueden ser utilizados como aproximaciones de toda la funci??n. Estas aproximaciones son buenas si se incluyen suficientemente muchos t??rminos.
- La representaci??n en serie simplifica muchas pruebas matem??ticas .
En la foto de la derecha es una aproximaci??n exacta del pecado (x) alrededor del punto a = 0. La curva de color rosa es un polinomio de grado siete:
 .
.
El error en esta aproximaci??n no es m??s que  . En particular, para
. En particular, para  , El error es menos de 0,000003.
, El error es menos de 0,000003.
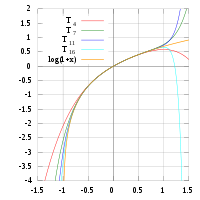
En contraste, Tambi??n se muestra una imagen de la funci??n de log (1 + x) y algunos de sus polinomios de Taylor alrededor de a = 0 Estas aproximaciones convergen a la funci??n s??lo en la regi??n de -1 <x ≤ 1.; fuera de esta regi??n los de grado superior polinomios de Taylor son peores aproximaciones para la funci??n. Este es un ejemplo de Fen??meno de Runge.
El teorema de Taylor da una variedad de l??mites generales del tama??o del error en  incurridos en la aproximaci??n de una funci??n por su en??simo orden del polinomio de Taylor.
incurridos en la aproximaci??n de una funci??n por su en??simo orden del polinomio de Taylor.
Historia
La Fil??sofo Pit??goras Zeno considera el problema de la suma de una serie infinita para lograr un resultado finito, pero rechaz?? como una imposibilidad: el resultado fue La paradoja de Zen??n. M??s tarde, Arist??teles propuso una resoluci??n filos??fica de la paradoja, pero el contenido matem??tico era aparentemente sin resolver hasta retomada por Dem??crito y luego Arqu??medes . Fue a trav??s de Arqu??medes m??todo de agotamiento que un n??mero infinito de subdivisiones progresivas podr??a realizarse para lograr un resultado trigonom??trica finito. Liu Hui empleada independientemente un m??todo similar varios siglos despu??s.
En el siglo 14 , los primeros ejemplos de la utilizaci??n de series y estrechamente relacionados m??todos de Taylor fueron dadas por Madhava de Sangamagrama. Aunque hay constancia de su obra sobrevive, escritos de posteriores matem??ticos indios sugieren que se encontr?? con una serie de casos especiales de la serie de Taylor, incluidos los de las funciones trigonom??tricas de seno, coseno, tangente , y arcotangente. La Escuela de Kerala ampli?? sus obras con varios desarrollos en serie y aproximaciones racionales hasta el siglo 16 .
En el siglo 17 , James Gregory tambi??n trabaj?? en esta ??rea y public?? varias series de Maclaurin. No fue hasta 1715 sin embargo, que un m??todo general para la construcci??n de estas series para todas las funciones para las que existen fue finalmente proporcionados por Brook Taylor, despu??s de que la serie ahora tienen nombre.
La serie de Maclaurin fue nombrado despu??s Colin Maclaurin, profesor en Edimburgo, que public?? el caso especial del resultado Taylor en el siglo 18.
Propiedades
Si esta serie converge para cada x en el intervalo (a - r, a + r) y la suma es igual a f (x), entonces la funci??n f (x) se dice que es anal??tica en el intervalo (a - r, a + r). Si esto es cierto para cualquier r entonces la funci??n se dice que es una funci??n entera. Para comprobar si la serie converge hacia f (x), que normalmente se utiliza estimaciones para el resto del plazo teorema de Taylor . Una funci??n es anal??tica si y s??lo si puede ser representado como una serie de potencias ; los coeficientes de la serie de potencia son entonces necesariamente las dadas en la f??rmula de Taylor anteriormente.
La importancia de tal representaci??n en serie de potencias es al menos cuatro veces. En primer lugar, la diferenciaci??n y la integraci??n de las series de potencias se pueden realizar t??rmino a t??rmino y es por lo tanto particularmente f??cil. En segundo lugar, una funci??n anal??tica puede extenderse ??nicamente a una funci??n holomorfa definida en un disco abierto en el plano complejo , lo que hace que toda la maquinaria de an??lisis complejo disponible. En tercer lugar, la (truncado) series se puede utilizar para calcular valores de la funci??n de aproximadamente (a menudo mediante la refundici??n del polinomio en el Forma Chebyshev y evaluar con el Algoritmo Clenshaw).
En cuarto lugar, las operaciones algebraicas menudo se pueden hacer mucho m??s f??cilmente en la representaci??n en serie de potencias; por ejemplo, la prueba m??s simple de La f??rmula de Euler utiliza los desarrollos en serie de Taylor para el seno, coseno y funciones exponenciales. Este resultado es de importancia fundamental en campos como an??lisis arm??nico.
Tenga en cuenta que hay ejemplos de funciones infinitamente diferenciable f (x), cuya serie de Taylor converge, pero no son iguales a f (x). Por ejemplo, la funci??n definida por puntos por f (x) = e -1 / x ?? si x ≠ 0 y f (0) = 0 es un ejemplo de una funci??n suave no anal??tico. Todos sus derivados en x = 0 son cero, por lo que la serie de Taylor de f (x) a 0 es cero en todas partes, a pesar de que la funci??n es diferente de cero para cada x ≠ 0. Esta patolog??a en particular no aflige serie de Taylor en an??lisis complejo. All??, la zona de convergencia de una serie de Taylor es siempre un disco en el plano complejo (posiblemente con un radio de 0), y donde la serie de Taylor converge, converge al valor de funci??n. Observe que e -1 / z ?? no se acerca 0 como z se aproxima a 0 a lo largo del eje imaginario, por lo tanto, esta funci??n no es continua como una funci??n en el plano complejo.
Dado que cada secuencia de n??meros reales o complejos puede aparecer como coeficientes de la serie de Taylor de una funci??n infinitamente diferenciable definida en la recta real, el radio de convergencia de una serie de Taylor puede ser cero. Hay incluso infinitamente funciones diferenciables definidos en la recta real cuya serie de Taylor tiene un radio de convergencia 0 en todas partes.
Algunas funciones no se pueden escribir como serie de Taylor porque tienen una singularidad; en estos casos, se puede a menudo todav??a lograr un desarrollo en serie si se permite tambi??n potencias negativas de la variable x; ver Serie de Laurent. Por ejemplo,  se puede escribir como una serie de Laurent.
se puede escribir como una serie de Laurent.
La M??todo Parker-Sochacki es un avance reciente en la b??squeda de la serie de Taylor, que son soluciones de las ecuaciones diferenciales . Este algoritmo es una extensi??n de la Iteraci??n de Picard.
Lista de series de Taylor de algunas funciones comunes

Varios importantes desarrollos en serie de Maclaurin siguen. Todas estas expansiones son v??lidos para argumentos complejos  .
.
Finito serie geom??trica:
Infinito serie geom??trica:
Las variantes de la serie geom??trica infinita:
Serie binomial (incluye la ra??z cuadrada para α = 1/2 y la serie geom??trica infinita para α = -1):

- con generalizadas coeficientes binomiales

- donde el B s son N??meros de Bernoulli.
Funciones hiperb??licas:
W funci??n de Lambert:
Los n??meros  apareciendo en las expansiones de suma de tan (x) y tanh (x) son los N??meros de Bernoulli. La
apareciendo en las expansiones de suma de tan (x) y tanh (x) son los N??meros de Bernoulli. La  en la expansi??n de sec (x) son N??meros de Euler.
en la expansi??n de sec (x) son N??meros de Euler.
C??lculo de la serie de Taylor
Existen varios m??todos para el c??lculo de la serie de Taylor de un gran n??mero de funciones. Uno puede tratar de utilizar la serie de Taylor como est?? y generalizar la forma de los coeficientes, o uno puede utilizar manipulaciones tales como la sustituci??n, multiplicaci??n o divisi??n, suma o resta de la serie est??ndar de Taylor para la construcci??n de la serie de Taylor de una funci??n, en virtud de la serie de Taylor de ser series de potencias. En algunos casos, tambi??n se puede derivar la serie de Taylor aplicando repetidamente integraci??n por partes. Particularmente conveniente es el uso de sistemas de ??lgebra computacional para el c??lculo de la serie de Taylor.
Primer ejemplo
Calcule el 7?? grado polinomio de Maclaurin de la funci??n
 .
.
En primer lugar, vuelva a escribir la funci??n como
 .
.
Tenemos para el logaritmo natural (mediante el uso de la gran notaci??n O)
y para la funci??n de coseno
El desarrollo en serie de este ??ltimo tiene un cero t??rmino constante, lo que nos permite sustituir la segunda serie en la primera y de omitir f??cilmente t??rminos de orden mayor que el grado 7?? usando la notaci??n O grande:
Desde el coseno es una incluso la funci??n, los coeficientes para todas las potencias impares de x, x 3, x 5, x 7,. . . tiene que ser cero.
Segundo ejemplo
Supongamos que queremos la serie de Taylor a 0 de la funci??n
 .
.
Tenemos para la funci??n exponencial
y, como en el primer ejemplo,
Suponga que la serie de potencias es
Luego de multiplicaci??n con el denominador y la sustituci??n de la serie de los rendimientos coseno
Recopilaci??n de los plazos de hasta cuarto orden rendimientos
La comparaci??n de coeficientes con la serie anterior de la funci??n exponencial se obtiene la serie de Taylor deseado
 .
.
Serie de Taylor como definiciones
Cl??sicamente, las funciones anteriores se definen por alguna propiedad que tiene para ellos. Por ejemplo, la funci??n exponencial se define como la funci??n que es igual a su propia derivada. Sin embargo, en an??lisis computable, funciones debe ser definido por algoritmos en lugar de las propiedades, por lo que las expansiones de Taylor anteriores se utilizan como definiciones primarias en lugar de los resultados obtenidos. Este es tambi??n probable que sea el caso en las implementaciones de software de las funciones.
El uso de la serie de Taylor, se puede definir funciones anal??ticas de matrices y los operadores, tales como matriz exponencial o logaritmo matriz.
Serie de Taylor en varias variables
La serie de Taylor tambi??n puede ser generalizado a funciones de m??s de una variable con

 .
.
Por ejemplo, para una funci??n que depende de dos variables, X e Y, la serie de Taylor de segundo orden sobre el punto (a, b) es:
donde los sub??ndices denotan la respectiva derivadas parciales.
Un segundo orden desarrollo en serie de Taylor de una funci??n escalar de m??s de una variable puede ser escrito como de forma compacta
donde  es el gradiente y
es el gradiente y  es el Matriz de Hesse. La aplicaci??n de la notaci??n multi-??ndice de la serie de Taylor para varias variables se convierte en
es el Matriz de Hesse. La aplicaci??n de la notaci??n multi-??ndice de la serie de Taylor para varias variables se convierte en
en plena analog??a con el solo caso variable.





































![+ \ Frac {1} {2!} \ Left [f_ {xx} (a, b) (xa) ^ 2 + 2f_ {xy} (a, b) (xa) (YB) + f_ {yy} (un , b) (yb) ^ 2 \ right] \!](../../images/96/9601.png)


