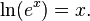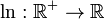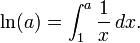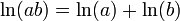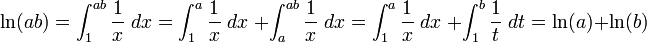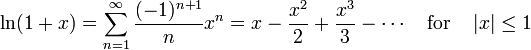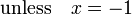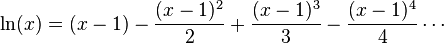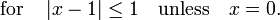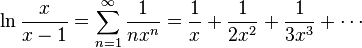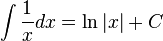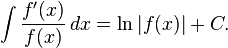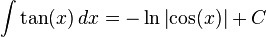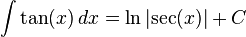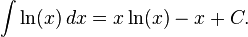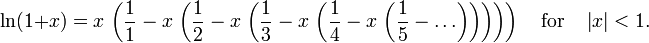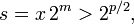Logaritmo natural

Temas relacionados: Matem??ticas

Acerca de este escuelas selecci??n Wikipedia

SOS Children han producido una selecci??n de art??culos de la Wikipedia para escuelas desde 2005. Haga clic aqu?? para obtener m??s informaci??n sobre SOS Children.

El logaritmo natural, antes conocido como el logaritmo hiperb??lico, es el logaritmo de la base e, donde e es un irracional constante aproximadamente igual a 2,718 281 828 459. En t??rminos simples, el logaritmo natural de un n??mero x es la potencia a la que e habr??a que ser elevado a la igualdad x - por ejemplo, el logaritmo natural de correo en s?? es 1 porque e ¹ = e, mientras que el logaritmo natural de 1 ser??a 0, ya que e = ⁰ 1. El logaritmo natural se puede definir para todos los positivos n??meros reales x como el ??rea bajo la curva y = 1 / t de 1 a x, y tambi??n se pueden definir para distintos de cero los n??meros complejos como se explica a continuaci??n .

Gr??fica de la funci??n logaritmo natural. La funci??n va r??pidamente a menos infinito cuando x tiende a 0, pero crece lentamente hasta el infinito positivo cuando x aumenta.

La funci??n logaritmo natural tambi??n puede ser definido como la funci??n inversa de la funci??n exponencial , lo que lleva a las identidades:

$e ^ {\ ln (x)} = x \ qquad \ mbox {si} x> 0 \, \!$

$\ Ln (e ^ x) = x. \, \!$

En otras palabras, la funci??n logaritmo es una biyecci??n entre el conjunto de los n??meros reales positivos para el conjunto de todos los n??meros reales. M??s precisamente, se trata de una isomorfismo del grupo de los n??meros reales positivos bajo la multiplicaci??n al grupo de los n??meros reales menores de adici??n. Representada como una funci??n :

$\ Ln: \ mathbb {R} ^ + \ a \ mathbb {R}$

Los logaritmos se pueden definir a cualquier base positivo distinto de 1, no s??lo e, y son ??tiles para la resoluci??n de ecuaciones en las que la inc??gnita aparece como el exponente de alguna otra cantidad.

Convenciones de notaci??n

Los matem??ticos, estad??sticos, y algunos ingenieros generalmente entienden bien "log (x)" o "ln (x)" en el sentido de log _e (x), es decir, el logaritmo natural de x, y escribir "log ₁₀ (x)" si el logaritmo en base 10 de x est?? destinado.

Algunos ingenieros, bi??logos, y algunos otros generalmente escriben "ln (x)" (o de vez en cuando "log _e (x)") cuando quieren decir el logaritmo natural de x, y toman "log (x)" en el sentido log ₁₀ (x) o, en el caso de algunos cient??ficos de la computaci??n , log ₂ (x) (lg aunque esto muchas veces se escribe (x) en su lugar).

En la mayor??a de uso com??n de lenguajes de programaci??n , incluyendo C , C ++ , MATLAB, Fortran, y BASIC , "log" o "log" se refiere al logaritmo natural.

En de mano calculadoras , el logaritmo natural se denota ln, mientras que de registro es el logaritmo en base 10.

??Por qu?? se le llama "natural"

En un principio, podr??a parecer que ya que nuestro sistema de numeraci??n es de base 10 , esta base ser??a m??s "natural" que la base e. Pero matem??ticamente, el n??mero 10 no es particularmente significativo. Su uso culturalmente como base para muchas sociedades de numeraci??n sistemas-probablemente surge de los seres humanos n??mero t??pico de los dedos. Y otras culturas han basado sus sistemas de conteo en estas elecciones como el 5, 20 y 60.

Entrar _electr??nico es un registro "natural" porque brota autom??ticamente de, y aparece tan a menudo, en las matem??ticas. Por ejemplo, considere el problema de la diferenciaci??n de una funci??n logar??tmica:

$\ Frac {d} {dx} \ log_b (x) = \ frac {\ log_b (e)} {x} = \ frac {1} {\ ln (b) x}$

Si el base b es igual a E, entonces la derivada es simplemente 1 / x, y en x = 1 este derivado es igual a 1. Otro sentido en el que el logaritmo e basal es la m??s natural es que puede ser definido con bastante facilidad en t??rminos de un sencillo integral o serie de Taylor y esto no es cierto de otros logaritmos.

Otros sentidos de esta naturalidad no hacen uso del c??lculo. Como un ejemplo, hay un n??mero de serie simple que implica el logaritmo natural. De hecho, Pietro Mengoli y Nicholas Mercator llam?? Logarithmus naturalis unas d??cadas antes de Newton y Leibniz desarrollaron c??lculo.

Definiciones

Ln (x) se define como el ??rea bajo la curva f (x) = 1 / x.

Formalmente, ln (a) puede ser definida como el ??rea bajo la gr??fica de 1 / x de 1 a a, es decir, como la integral ,

$\ Ln (a) = \ int_1 ^ a \ frac {1} {x} \, dx.$

Esto define un logaritmo porque satisface la propiedad fundamental de un logaritmo:

$\ Ln (ab) = \ ln (a) + \ ln (b) \, \!$

Esto se puede demostrar por dejar 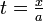$t = \ tfrac xa$ como sigue:

$\ Ln (ab) = \ int_1 ^ {ab} \ frac {1} {x} \; dx = \ int_1 ^ a \ frac {1} {x} \; dx \; + \ Int_a ^ {ab} \ frac {1} {x} \; dx = \ int_1 ^ {a} \ frac {1} {x} \; dx \; + \ Int_1 ^ {b} \ frac {1} {t} \; dt = \ ln (a) + \ ln (b)$

El n??mero e puede entonces ser definida como el ??nico n??mero real a tal que ln (a) = 1.

Alternativamente, si la funci??n exponencial ha sido definido primero utilizando un serie infinita, el logaritmo natural se puede definir como su funci??n inversa , es decir, ln (x) es que la funci??n de tal manera que 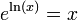$e ^ {\ ln (x)} = x \!$ . Puesto que el rango de la funci??n exponencial en argumentos reales es todos los n??meros reales positivos y ya que la funci??n exponencial es estrictamente creciente, esto est?? bien definido para todo x positivo.

Derivada, serie de Taylor

El derivado del logaritmo natural est?? dada por

$\ Frac {d} {dx} \ ln (x) = \ frac {1} {x}. \,$

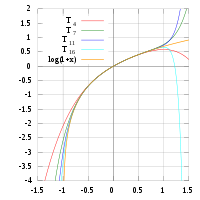
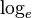Los polinomios de Taylor de $\ Log_e$ (1 + x) s??lo proporcionan aproximaciones precisas en el rango -1 <x ≤ 1. Tenga en cuenta que, para x> 1, los polinomios de Taylor de grado superior son peores aproximaciones.

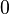Esto conduce a la serie de Taylor para $\ Ln (1 + x)$ alrededor $0$ ; tambi??n conocido como el Serie de Mercator

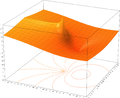
$\ Ln (1 + x) = \ sum_ {n = 1} ^ \ infty \ frac {(- 1) ^ {n + 1}} {n} x ^ n = x - \ frac {x ^ 2} {2 } + \ frac {x ^ 3} {3} - \ cdots \ quad {\ rm para} \ quad \ left | x \ right | \ leq 1 \ quad$

${\ Rm menos} \ quad x = -1$

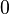A la derecha hay una imagen de $\ Ln$ $(1 + x)$ y algunos de sus polinomios de Taylor en torno a $0$ . Estas aproximaciones convergen a la funci??n s??lo en la regi??n de -1 <x ≤ 1; fuera de esta regi??n los de grado superior polinomios de Taylor son peores aproximaciones para la funci??n.

Sustituyendo x -1 para x, se obtiene una forma alternativa para ln (x) en s??, a saber,

$\ Ln (x) = \ sum_ {n = 1} ^ \ infty \ frac {(- 1) ^ {n + 1}} {n} (x-1) ^ n$

$\ Ln (x) = (x - 1) - \ frac {(x-1) ^ 2} {2} + \ frac {(x-1) ^ 3} {3} - \ frac {(x-1) ^ 4} {4} \ cdots$

${\ Rm para} \ quad \ left | x-1 \ right | \ leq 1 \ quad {\ rm menos} \ quad x = 0.$

Mediante el uso de la Euler transforman en la serie de Mercator, se obtiene lo siguiente, que es v??lido para cualquier x con valor absoluto superior a 1:

$\ Ln {x \ over {x-1}} = \ sum_ {n = 1} ^ \ infty {1 \ over {nx ^ n}} = {1 \ over x} + {1 \ over {2x ^ 2} } + {1 \ over {3x ^ 3}} + \ cdots$

Esta serie es similar a una F??rmula de tipo BBP.

Tambi??n tenga en cuenta que $x \ over {x-1}$ es su propia funci??n inversa, por lo que di?? el logaritmo natural de un n??mero determinado n, simplemente poner en $n \ over {n-1}$ para x.

El logaritmo natural en la integraci??n

El logaritmo natural permite sencilla la integraci??n de funciones de la forma g (x) = f '(x) / f (x): un primitiva de g (x) viene dada por ln (| f (x) |). Este es el caso debido a la regla de la cadena y el siguiente hecho:

$\ {D \ over dx} \ left (\ ln \ left | x \ right | \ right) = {1 \ over x}.$

En otras palabras,

$\ Int {1 \ over x} dx = \ ln | x | + C$

$\ Int {\ frac {f '(x)} {f (x)} \, dx} = \ ln | f (x) | + C.$

He aqu?? un ejemplo en el caso de g (x) = tan (x):

$\ Int \ tan (x) \, dx = \ int {\ sin (x) \ over \ cos (x)} \, dx$

$\ Int \ tan (x) \, dx = \ int {- {d \ over dx} \ cos (x) \ over {\ cos (x)}} \, dx.$

Dejar que f (x) = cos (x) y f '(x) = - sen (x):

$\ Int \ tan (x) \, dx = - \ ln {\ left | \ cos (x) \ right |} + C$

$\ Int \ tan (x) \, dx = \ ln {\ left | \ sec (x) \ right |} + C$

donde C es una constante arbitraria de integraci??n.

El logaritmo natural se puede integrar usando integraci??n por partes:

$\ Int \ ln (x) \, dx = x \ ln (x) - x + C.$

Valor num??rico

Para calcular el valor num??rico del logaritmo natural de un n??mero, la expansi??n en serie de Taylor se puede reescribir como:

$\ ln (1 + x) = x \, \ left (\ frac {1} {1} - x \, \ left (\ frac {1} {2} - x \, \ left (\ frac {1} { 3} - x \, \ left (\ frac {1} {4} - x \, \ left (\ frac {1} {5} - \ ldots \ right) \ right) \ right) \ right) \ right) \ quad {\ rm para} \ quad \ left | x \ right | <1 \, \.!$

Para obtener una mejor tasa de convergencia, la siguiente identidad se puede utilizar.

Click on the following link to visit or download this HTML page

$\ Ln (x) = \ ln \ left (\ frac {1 + y} {1-y} \ right)$	$= 2 \, y \, \ left (\ frac {1} {1} + \ frac {1} {3} y ^ {2} + \ frac {1} {5} y ^ {4} + \ frac { 1} {7} y ^ {6} + \ frac {1} {9} y ^ {8} + \ ldots \ right)$
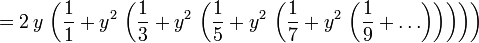
	$= 2 \, y \, \ left (\ frac {1} {1} + y ^ {2} \, \ left (\ frac {1} {3} + y ^ {2} \, \ left (\ frac {1} {5} + y ^ {2} \, \ left (\ frac {1} {7} + y ^ {2} \, \ left (\ frac {1} {9} + \ ldots \ right) \ right) \ right) \ right) \ right)$

a condici??n de que y = (x -1) / (x 1) y x> 0.

Para ln (x), donde x> 1, m??s cerca del valor de x es 1, m??s r??pida ser?? la velocidad de convergencia. Las identidades asociadas con el logaritmo se pueden aprovechar para explotar esta:

Click on the following link to visit or download this HTML page

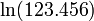
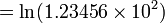
$\ Ln (123.456) \!$	$= \ Ln (1,23456 \ times 10 ^ 2) \, \!$
	$= \ Ln (1.23456) + \ ln (10 ^ 2) \, \!$
	$= \ Ln (1.23456) + 2 \ times \ ln (10) \, \!$
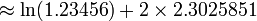
	$\ aprox \ ln (1.23456) + 2 \ veces 2.3025851 \, \!$

Se utilizaron Dichas t??cnicas antes de las calculadoras, al referirse a las tablas num??ricas y realizar manipulaciones como las anteriores.

Alta precisi??n

Para calcular el logaritmo natural con muchos d??gitos de precisi??n, el enfoque de Taylor no es eficiente ya que la convergencia es lenta. Una alternativa es utilizar el m??todo de Newton para invertir la funci??n exponencial, cuya serie converge m??s r??pidamente.

Una alternativa para el c??lculo de precisi??n extremadamente alta es la f??rmula

$\ Ln x \ aprox \ frac {\ pi} {2 M (1,4 / s)} - m \ ln 2$

donde M indica la -aritm??tica y la media geom??trica

$s = x \, 2 ^ m> 2 ^ {p / 2},$

con m elige de manera que los bits se alcanza p de precisi??n. De hecho, si se utiliza este m??todo, Newton inversi??n del logaritmo natural puede por el contrario ser usado para calcular la funci??n exponencial de manera eficiente. (Las constantes ln 2 y π pueden ser pre-computado a la precisi??n deseada utilizando cualquiera de varias series convergentes r??pidamente conocido.)

Complejidad computacional

La complejidad computacional de calcular el logaritmo natural (usando la media aritm??tica geom??trica) es O (M (n) ln n). Aqu?? n es el n??mero de d??gitos de precisi??n en el que el logaritmo natural se va a evaluar y M (n) es la complejidad computacional de la multiplicaci??n de dos n??meros de n -d??gitos.

Logaritmos complejos

La funci??n exponencial se puede extender a una funci??n que da un n??mero complejo como e ^x para cualquier n??mero complejo arbitrario x; s??lo tiene que utilizar la serie infinita con x compleja. Esta funci??n exponencial puede ser invertida para formar un logaritmo complejo que exhibe la mayor parte de las propiedades del logaritmo ordinario. Hay dos dificultades que implica: no tiene x e ^x = 0; y resulta que e ^{2 πi} = 1 = e ^0. Desde la propiedad multiplicativa todav??a trabaja para la funci??n exponencial compleja, e ^z = e ^{z 2 nπi,} para todo z complejo y enteros n.

As?? que el logaritmo no se puede definir para todo el plano complejo , y a??n as?? tiene varios valores - cualquier logaritmo complejo se puede cambiar en un logaritmo "equivalente" al a??adir cualquier m??ltiplo entero de 2 πi a voluntad. El logaritmo complejo s??lo puede ser de un solo valor en el plano de corte . Por ejemplo, ln i = 1/2 o 5/2 πi πi o -3/2 πi, etc .; y aunque i ⁴ = 1, 4 log i se puede definir como 2 πi, o 10 πi o -6 πi, y as?? sucesivamente.

Los gr??ficos de la funci??n logaritmo natural en el plano complejo (rama principal)
z = Re (ln (x + iy))
z = | Im (ln (x + iy)) |
z = | ln (x + iy) |
Superposici??n de los 3 gr??ficos anteriores

Recuperado de " http://en.wikipedia.org/w/index.php?title=Natural_logarithm&oldid=206770613 "