C??lculo vectorial

Temas relacionados: Matem??ticas

Antecedentes de las escuelas de Wikipedia

SOS Children produjo este sitio web para las escuelas, as?? como este sitio web video sobre ??frica . Ver http://www.soschildren.org/sponsor-a-child para averiguar sobre el apadrinamiento de ni??os.

Vector c??lculo (tambi??n llamado an??lisis vectorial) es un campo de las matem??ticas que se trate con multivariante an??lisis real de vectores en una espacio de producto interno de dos o m??s dimensiones (algunos resultados - los que implican el producto cruzado - s??lo pueden ser aplicados a las tres dimensiones). Consiste en un conjunto de f??rmulas y t??cnicas de resoluci??n de problemas muy ??tiles para la ingenier??a y la f??sica . An??lisis vectorial tiene su origen en an??lisis cuaterni??n, y fue formulado por el ingeniero y cient??fico estadounidense J. Willard Gibbs y el ingeniero brit??nico Oliver Heaviside.

C??lculo vectorial se ocupa de campos escalares, que asocian un escalar a cada punto del espacio, y campos de vectores, que asocian un vector a cada punto del espacio. Por ejemplo, la temperatura de una piscina es un campo escalar: a cada punto asociamos un valor escalar de la temperatura. El flujo de agua en el mismo grupo es un campo de vectores: a cada punto asociamos un vector de velocidad.

Operaciones con vectores

Estudios de c??lculo vectorial diversos operadores diferenciales definidas en campos escalares o vectoriales, que se expresan normalmente en t??rminos de la del operador ( $\ Nabla$ ). Las cuatro operaciones m??s importantes de c??lculo vectorial son:

Operaci??n	Notaci??n	Descripci??n	Dominio / Cocina
Gradiente	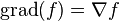$\ Operatorname {grad} (f) = \ nabla f$	Mide la velocidad y la direcci??n del cambio en un campo escalar.	Mapas campos escalares a campos vectoriales.
Curl	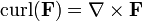$\ Operatorname {rizo} (\ mathbf {F}) = \ nabla \ times \ mathbf {F}$	Mide la tendencia a girar alrededor de un punto en un campo vectorial.	Mapas campos vectoriales a los campos vectoriales.
Divergencia	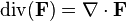$\ Operatorname {div} (\ mathbf {F}) = \ nabla \ cdot \ mathbf {F}$	Mide la magnitud de una fuente o sumidero en un punto dado en un campo vectorial.	Mapas campos vectoriales a campos escalares.
Laplaciano	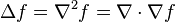$\ Delta f = \ nabla ^ 2 f = \ nabla \ cdot \ nabla f$	Una composici??n de las operaciones de divergencia y gradiente.	Mapas campos escalares a campos escalares.

Una cantidad llamada la Jacobiano es ??til para estudiar las funciones cuando tanto el dominio y el rango de la funci??n son multivariable, tales como un cambio de variables durante la integraci??n.

Teoremas

Del mismo modo, hay varios teoremas importantes relacionados con estos operadores que generalizan el teorema fundamental del c??lculo de dimensiones superiores:

Teorema	Declaraci??n	Descripci??n
Teorema de degradado	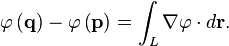$\ Phi \ left (\ mathbf {q} \ right) - \ phi \ left (\ mathbf {p} \ right) = \ int_L \ nabla \ phi \ cdot d \ mathbf {r}.$	La integral de l??nea a trav??s de un gradiente de campo (vector) es igual a la diferencia en su campo escalar en los extremos de la curva .
Teorema de Green	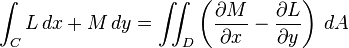$\ Int_ {C} L \, dx + M \, dy = \ iint_ {D} \ left (\ frac {\ M parcial} {\ x parcial} - \ frac {\ L parcial} {\ y parcial} \ right ) \, dA$	La integral de la curvatura escalar de un campo vectorial sobre alguna regi??n en el plano es igual a la integral de l??nea del campo vectorial sobre la curva que delimita la regi??n.
El teorema de Stokes	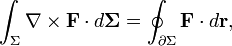$\ Int _ {\ Sigma} \ nabla \ times \ mathbf {F} \ cdot d \ mathbf {\ Sigma} = \ oint _ {\ partial \ Sigma} \ mathbf {F} \ cdot d \ mathbf {r},$	La integral de la curvatura de un campo vectorial sobre una superficie es igual a la integral de l??nea del campo vectorial sobre la curva que limita la superficie.
Teorema de la divergencia	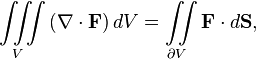$\ Iiint \ limits_V \ left (\ nabla \ cdot \ mathbf {F} \ right) dV = \ Iint \ l??mites _ {\ part V} \ mathbf {F} \ cdot d \ vec {S},$	La integral de la divergencia de un campo vectorial sobre un poco de s??lido es igual a la integral de la flujo a trav??s de la superficie que delimita el s??lido.

El uso del c??lculo vectorial puede requerir el uso de las manos de la sistema de coordenadas que deben tenerse en cuenta (v??ase el producto cruz y la prepotencia para m??s detalles). La mayor??a de los resultados anal??ticos son f??ciles de entender, en una forma m??s general, el uso de la maquinaria de la geometr??a diferencial , de los cuales c??lculo vectorial forma un subconjunto.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Vector_calculus&oldid=201811633 "