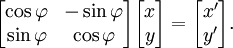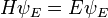Valores propios y vectores propios
Antecedentes
SOS Children hizo esta selecci??n Wikipedia junto a otros recursos de escuelas . Ver http://www.soschildren.org/sponsor-a-child para averiguar sobre el apadrinamiento de ni??os.

En las matem??ticas , un vector puede ser pensado como una flecha. Tiene una longitud, llamado su magnitud, y apunta en una direcci??n particular. La transformaci??n lineal puede ser considerada para operar en un vector para cambiarlo, por lo general cambiando tanto su magnitud y su direcci??n. Un vector propio de una transformaci??n lineal dado es un vector que se multiplica por una constante llamada valor propio durante esa transformaci??n. La direcci??n del vector propio es o bien sin cambios por que la transformaci??n (por valores propios positivos) o invertido (para valores propios negativos).
Por ejemplo, un valor propio de 2 significa que el vector propio se duplica en longitud y puntos en la misma direcci??n. Un valor propio de 1 significa que el vector propio es sin cambios, mientras que un valor propio de -1 significa que el vector propio se invierte en la direcci??n. Un espacio caracter??stico de una transformaci??n dada es el lapso de los vectores propios de que la transformaci??n con el mismo valor propio, junto con el vector cero (que no tiene direcci??n). Un espacio caracter??stico es un ejemplo de una subespacio de un espacio vectorial .
En ??lgebra lineal , cada transformaci??n lineal entre espacios vectoriales de dimensi??n finita puede ser dada por una matriz , que es una matriz rectangular de n??meros dispuestos en filas y columnas. Los m??todos est??ndar para la b??squeda de valores propios, vectores propios, y eigenspaces de una matriz dada se discuten a continuaci??n.
Estos conceptos desempe??an un papel importante en varias ramas de tanto puras y matem??ticas aplicadas - que aparece prominentemente en ??lgebra lineal , an??lisis funcional, y en menor medida en las matem??ticas no lineales.
Muchos tipos de objetos matem??ticos pueden ser tratados como vectores: funciones , modos arm??nicos, estados cu??nticos, y frecuencias, por ejemplo. En estos casos, el concepto de direcci??n pierde su sentido corriente, y se le da una definici??n abstracta. A??n as??, si esta direcci??n abstracta es sin cambios por una transformaci??n lineal dado, se utiliza el prefijo "eigen", como en funci??n propia, modo propio, estado propio, y frecuencia propia.
Historia
Valores propios se introducen a menudo en el contexto de ??lgebra lineal o teor??a de la matriz . Hist??ricamente, sin embargo, surgieron en el estudio de formas y cuadr??tica ecuaciones diferenciales .
Euler hab??a estudiado tambi??n el movimiento de rotaci??n de una cuerpo r??gido y descubierto la importancia de la ejes principales. Como se dio cuenta de Lagrange, los ejes principales son los vectores propios de la matriz de inercia. A principios del siglo 19, Cauchy vio c??mo su trabajo se podr??a utilizar para clasificar el superficies cuadr??ticas, y generalizarse a dimensiones arbitrarias. Cauchy tambi??n acu???? el t??rmino caract??ristique Racine (ra??z caracter??stica) por lo que ahora se llama valor propio; su t??rmino sobrevive en ecuaci??n caracter??stica.
Fourier utiliza el trabajo de Laplace y Lagrange para resolver el ecuaci??n del calor por separaci??n de variables en su famoso libro 1822 Th??orie analytique de la chaleur. Sturm desarroll?? las ideas de Fourier m??s y los trajo a la atenci??n de Cauchy, que los combina con sus propias ideas y lleg?? al hecho de que las matrices sim??tricas tienen valores propios reales. Esto se extendi?? por Hermite en 1855 a lo que ahora se llaman Matrices hermitianas. Por la misma ??poca, Brioschi demostr?? que los valores propios de matrices ortogonales se encuentran en la unidad de c??rculo, y Clebsch encontr?? el resultado correspondiente hemi-sim??tricas matrices. Finalmente, Weierstrass aclar?? un aspecto importante en el teor??a de la estabilidad iniciado por Laplace por darse cuenta de que matrices defectuosos pueden causar inestabilidad.
Mientras tanto, Liouville estudi?? problemas de valores propios similares a los de Sturm; la disciplina que surgi?? de su trabajo se llama ahora Teor??a de Sturm-Liouville. Schwarz estudi?? el primer valor propio de La ecuaci??n de Laplace en dominios generales hacia el final del siglo 19, mientras Poincar?? estudi?? La ecuaci??n de Poisson unos a??os m??s tarde.
Al comienzo del siglo 20, Hilbert estudi?? los valores propios de operadores integrales de visualizaci??n de los operadores como matrices infinitas. ??l fue el primero en utilizar el alem??n eigen palabra para denotar valores y vectores propios en 1904, a pesar de que puede haber sido despu??s de un uso relacionado, por Helmholtz. "Eigen" se puede traducir como "propia", "peculiar", "caracter??stica" o "individuo" -emphasizing lo importante que son los valores propios de la definici??n de la naturaleza ??nica de una transformaci??n espec??fica. Desde hace alg??n tiempo, el t??rmino est??ndar en Ingl??s fue "valor apropiado", pero el t??rmino "valor propio" m??s distintivo es est??ndar en la actualidad.
El primer algoritmo num??rico para el c??lculo de valores y vectores propios apareci?? en 1929, cuando Von Mises public?? el m??todo de la potencia. Uno de los m??todos m??s populares de la actualidad, la Algoritmo QR, se propuso de forma independiente por Francis y Kublanovskaya en 1961.
Definiciones: la ecuaci??n de valor propio
Transformaciones lineales de un espacio vectorial, tales como rotaci??n, reflexi??n, estiramiento, compresi??n, cizalla o cualquier combinaci??n de ??stos, pueden ser visualizadas por el efecto que producen en vectores . En otras palabras, son funciones vectoriales. M??s formalmente, en un espacio vectorial L una funci??n vectorial A se define si para cada vector x de L corresponde un ??nico vector y = A (x) de L. En aras de la brevedad, los par??ntesis alrededor del vector en el que la transformaci??n est?? actuando a menudo se omiten. Una funci??n vectorial A es lineal si tiene las dos propiedades siguientes:
- aditividad

- homogeneidad

donde x e y son dos vectores del espacio vectorial L y α es cualquier n??mero real . Tal funci??n se llama indistintamente una transformaci??n lineal, operador lineal o lineal endomorphism en el espacio L.
Dada una transformaci??n lineal A, un no-cero vector x se define como un vector propio de la transformaci??n si satisface la ecuaci??n del valor propio λ = A x x para algunos λ escalar. En esta situaci??n, el λ escalar se llama un valor propio de A correspondiente al vector propio x. |
La ecuaci??n clave en esta definici??n es la ecuaci??n de valor propio, A x = λ x. La mayor??a de los vectores x no satisfar??n tal ecuaci??n. Un vector t??pico x cambia de direcci??n cuando es accionado por A, de modo que A x no es un m??ltiplo de x. Esto significa que s??lo ciertos vectores especiales x son vectores propios, y s??lo ciertos λ n??meros especiales son valores propios. Por supuesto, si A es un m??ltiplo de la matriz de identidad, entonces ning??n vector cambia de direcci??n, y todos los vectores no nulos son vectores propios. Pero en el caso de costumbre, vectores propios son pocos y distantes entre s??. Ellos son los "modos normales" del sistema, y act??an de forma independiente.
Se impone la necesidad de que el vector propio ser distinto de cero porque la ecuaci??n A 0 = λ 0 es v??lido para cada una y cada λ. Como la ecuaci??n siempre es trivialmente cierto, no es un caso interesante. En contraste, un valor propio puede ser cero en una forma no trivial. Un valor propio puede ser, y por lo general es, tambi??n un n??mero complejo . En la definici??n anterior, los vectores propios y valores propios no ocurren de manera independiente. En cambio, cada vector propio est?? asociado con un valor propio espec??fico. Por esta raz??n, un vector propio y x un valor propio λ correspondiente se refieren a menudo como un eigenpair. Un valor propio puede estar asociado con varios o incluso con n??mero infinito de vectores propios. Pero a la inversa, si se da un vector propio, el valor propio asociado para este vector propio es ??nico. De hecho, desde la igualdad A x = λ x = λ 'x y de x ≠ 0 se deduce que λ = λ'.

Geom??tricamente (Fig. 2), la ecuaci??n de valor propio significa que bajo la transformaci??n vectores propios de una experiencia s??lo los cambios en magnitud y el signo - la direcci??n de A x es la misma que la de x. Este tipo de transformaci??n lineal se define como homotecia (dilataci??n, transformaci??n de semejanza). El valor propio λ es simplemente la cantidad de "estirar" o "reducir" a la que un vector se somete cuando se transforma por A. Si λ = 1, el vector se mantiene sin cambios (no afectada por la transformaci??n). Una transformaci??n I en las que un vector x se mantiene sin cambios, I x = x, se define como transformaci??n de la identidad. Si λ = -1, el vector voltea a la direcci??n opuesta (gira a 180 ??); esto se define como la reflexi??n.
Si x es un vector propio de la transformaci??n lineal A con valor propio λ, entonces cualquier vector y = α x es tambi??n un vector propio de A con el mismo valor propio. A partir de la homogeneidad de la transformaci??n Una se sigue que A y = α (A x) = α (λ x) = λ (α x) = λ y. Del mismo modo, utilizando la propiedad de aditividad de la transformaci??n lineal, se puede demostrar que cualquier combinaci??n lineal de vectores propios con valor propio λ tiene el mismo valor propio λ. Por lo tanto, cualquier vector distinto de cero en la l??nea a trav??s de X y el vector cero es un vector propio con el mismo valor propio como x. Junto con el vector cero, los vectores propios forman un subespacio del espacio vectorial llamado un espacio caracter??stico. Los vectores propios que corresponden a diferentes valores propios son linealmente independientes significado, en particular, que en un espacio dimensional n la transformaci??n lineal A no puede tener m??s de n vectores propios con diferentes valores propios. Los vectores de la autoespacio generan una subespacio lineal de A que es invariante (sin cambios) en esta transformaci??n.
Si una base se define en el espacio vectorial L n, todos los vectores se pueden expresar en t??rminos de componentes . Vectores polares pueden ser representados como matrices de una sola columna con n filas donde n es la dimensionalidad del espacio. Transformaciones lineales se pueden representar con matrices cuadradas; para cada transformaci??n lineal de L A N corresponde una matriz cuadrada de rango n. Por el contrario, a cada matriz cuadrada de rango n corresponde una transformaci??n lineal de L n en una base dada. Debido a la aditividad y la homogeneidad de la trasformation lineal y la ecuaci??n de valor propio (que es tambi??n una transformaci??n lineal - homotecia), esas funciones vectoriales se pueden expresar en forma de matriz. As??, en un espacio de dos dimensiones vector L 2 equipado con base est??ndar, la ecuaci??n de vector propio para una transformaci??n lineal A puede ser escrito en la siguiente representaci??n matricial:
donde la yuxtaposici??n de matrices significa la multiplicaci??n de matrices . Esto es equivalente a un conjunto de ecuaciones lineales N, donde N es el n??mero de vectores de la base de la base fija. En estas ecuaciones son desconocidos tanto el valor propio λ y los componentes de x variables.
Los vectores propios de A como se ha definido anteriormente tambi??n se denominan vectores propios correctos, ya que son vectores columna que se interponen en el lado derecho de la matriz A en la ecuaci??n de valor propio. Si existe una matriz transpuesta A T que satifies la ecuaci??n de valor propio, es decir, si A T x = λ x, entonces λ x T = (λ x) T = (A x T) T = T x A, o x T A = λ x T. La ??ltima ecuaci??n es similar a la ecuaci??n de valor propio, pero en lugar del vector columna x que contiene su vector transpuesto, el vector fila x T, que se encuentra en el lado izquierdo de la matriz A. Los vectores propios que satisfacen la ecuaci??n de valor propio x T A = λ x T se denominan vectores propios izquierda. Ellos son vectores fila. En muchas aplicaciones comunes, s??lo los vectores propios correctos deben ser considerados. De ah?? el t??rmino no calificado "vector propio" se entender?? que se refiere a un vector propio derecho. Ecuaciones de valores propios, escritos en t??rminos de vectores propios derecha o izquierda (A x = λ x y x T A = λ x T) tienen el mismo valor propio λ.
Un vector propio se define como un director o vector propio dominante si se corresponde con el valor propio de magnitud m??s grande (para los n??meros reales, el mayor valor absoluto). Repetida aplicaci??n de una transformaci??n lineal a una arbitrarias vector da como resultado un vector proporcional (colineal) a la principal vector propio.
La aplicabilidad de la ecuaci??n del valor propio de la teor??a general de la matriz se extiende el uso de vectores propios y valores propios de todas las matrices, y por lo tanto en gran medida ampl??a el alcance del uso de estas construcciones matem??ticas no s??lo a las transformaciones de los espacios vectoriales lineales, sino a todos los campos de la ciencia que utilizan matrices: Sistemas de ecuaciones lineales, optimizaci??n, vectores y c??lculo tensorial, todos los campos de la f??sica que utilizan cantidades de matriz, la f??sica cu??ntica, la relatividad especial, y la electrodin??mica, as?? como muchas aplicaciones de ingenier??a.
Ecuaci??n caracter??stica
La determinaci??n de los valores y vectores propios es importante en pr??cticamente todas las ??reas de la f??sica y muchos problemas de ingenier??a, tales como c??lculos de estr??s, an??lisis de estabilidad, las oscilaciones de los sistemas de vibraci??n, etc. Es equivalente a diagonalizaci??n de la matriz, y es el primer paso de ortogonalizaci??n, la b??squeda de invariantes, optimizaci??n (minimizaci??n o maximizaci??n), an??lisis de sistemas lineales, y muchas otras aplicaciones comunes.
El m??todo usual de encontrar todos los vectores propios y valores propios de un sistema es el primero en deshacerse de los componentes desconocidos de los vectores propios, y luego encontrar los valores propios, conecte los de vuelta uno a uno en la ecuaci??n de valores propios en forma de matriz y resolver que como un sistema de ecuaciones lineales para encontrar los componentes de los vectores propios. A partir de la transformaci??n de identidad I x = x, donde I es la matriz de identidad, x en la ecuaci??n de valor propio puede ser sustituido por I x para dar:
Se necesita la matriz de identidad para mantener matrices, vectores y escalares recta; la ecuaci??n (A - λ) x = 0 es m??s corto, pero mezclado ya que no diferencia entre la matriz, escalar y vectorial. La expresi??n en el lado derecho se transfiere al lado izquierdo con un signo negativo, dejando a 0 en el lado derecho:
El vector propio x se retir?? detr??s de par??ntesis:
Esto puede ser visto como un sistema lineal de ecuaciones en el que la matriz de coeficientes es la expresi??n en el par??ntesis, la matriz de las inc??gnitas es x, y la matriz de lado derecho es cero. De acuerdo a La regla de Cramer, este sistema de ecuaciones tiene soluciones no triviales (no todos ceros o no cualquier n??mero) si y s??lo si su determinante se anula, por lo que las soluciones de la ecuaci??n est??n dados por:
Esta ecuaci??n se define como la ecuaci??n caracter??stica (con menos frecuencia, ecuaci??n secular) de A, y el lado izquierdo se define como la polinomio caracter??stico. El vector propio X o sus componentes no est??n presentes en la ecuaci??n caracter??stica, por lo que en esta etapa se dispensan con, y las ??nicas inc??gnitas que quedan por calcul?? son los valores propios (los componentes de la matriz A se dan, i. E, conocido de antemano ). Para un espacio vectorial L 2, la transformaci??n A es una matriz cuadrada de 2 x 2, y la ecuaci??n caracter??stica se puede escribir de la siguiente forma:
La expansi??n del determinante en los resultados a mano izquierda en un polinomio caracter??stico, que es un monic (su coeficiente principal es 1) polin??mica del segundo grado, y la ecuaci??n caracter??stica es la ecuaci??n de segundo grado
que tiene las siguientes soluciones ( ra??ces):
Para matrices reales, los coeficientes del polinomio caracter??stico son todos reales. El n??mero y tipo de las ra??ces depende del valor de la discriminante, D. Para los casos D = 0, D> 0, o D <0, respectivamente, las ra??ces son un real, dos reales, o dos complejos. Si las ra??ces son complejas, son tambi??n complejos conjugados de la otra. Cuando el n??mero de ra??ces es menor que el grado del polinomio caracter??stico (este ??ltimo es tambi??n el rango de la matriz, y el n??mero de dimensiones del espacio vectorial) la ecuaci??n tiene una ra??z m??ltiple. En el caso de una ecuaci??n cuadr??tica con una ra??z, esta ra??z es una ra??z doble, o una ra??z con multiplicidad 2. A ra??z con una multiplicidad de 1 es una ra??z simple. Una ecuaci??n de segundo grado con dos ra??ces reales o complejos tiene ra??ces s??lo simples. En general, la algebraica multiplicidad de un valor propio se define como la multiplicidad de la ra??z correspondiente del polinomio caracter??stico. El espectro de una transformaci??n en una dimensi??n finita espacio vectorial se define como la conjunto de todos sus valores propios. En el caso de dimensi??n infinita, el concepto de espectro es m??s sutil y depende de la topolog??a del espacio vectorial.
La f??rmula general para el polinomio caracter??stico de una matriz n -cuadrado es
donde S 0 = 1, S 1 = tr (A), la traza de la matriz de transformaci??n A y S k con k> 1 son las sumas de la directora los menores de orden k. El hecho de que los valores propios son ra??ces de un n -orden ecuaci??n muestra que una transformaci??n lineal de un espacio lineal n-dimensional tiene en la mayor??a de n diferentes valores propios. De acuerdo con la teorema fundamental del ??lgebra, en un espacio lineal complejo, el polinomio caracter??stico tiene al menos un cero. En consecuencia, cada transformaci??n lineal de un espacio lineal complejo tiene al menos un valor propio. Para los espacios lineales reales, si la dimensi??n es un n??mero impar, la transformaci??n lineal tiene al menos un valor propio; si la dimensi??n es un n??mero par, el n??mero de valores propios depende del determinante de la matriz de transformaci??n: si el determinante es negativo, existe al menos un positivo y un valor propio negativo, si el determinante es nada positivo se puede decir sobre la existencia de valores propios. La complejidad del problema para encontrar ra??ces / valores propios de la caracter??stica aumenta polin??micas r??pidamente con el aumento del grado del polinomio (la dimensi??n del espacio vectorial), n. Por lo tanto, para n = 3, valores propios son ra??ces de la ecuaci??n c??bica, para n = 4 - ra??ces de la ecuaci??n de cuarto grado. Para n> 4 no existen soluciones exactas y uno tiene que recurrir a algoritmos de b??squeda de ra??z, como el m??todo de Newton ( M??todo de Horner) para encontrar aproximaciones num??ricas de valores propios. Para grandes sim??trica matrices dispersas, Algoritmo de Lanczos se utiliza para calcular los valores propios y vectores propios.
Con el fin de encontrar los vectores propios, por lo tanto los valores propios encontrados como ra??ces de las ecuaciones caracter??sticas est??n conectados espalda, uno a la vez, en la ecuaci??n de valor propio escrita en forma de matriz (ilustrado para el caso m??s simple de un espacio de dos dimensiones vector L 2 ):
donde λ es uno de los valores propios encontrados como una ra??z de la ecuaci??n caracter??stica. Esta ecuaci??n matricial es equivalente a un sistema de dos ecuaciones lineales:
Las ecuaciones se resuelven para x e y por los m??todos algebraicos o matriz habituales. A menudo, es posible dividir ambos lados de las ecuaciones para uno o m??s de los coeficientes que hace que algunos de los coeficientes en frente de las inc??gnitas iguales a 1. Esto se llama normalizaci??n de los vectores, y corresponde a la elecci??n de uno de los vectores propios (el vector propio normalizado) como representante de todos los vectores en el espacio caracter??stico correspondiente al respectivo valor propio. La x e y por lo tanto se encuentran son los componentes del vector propio en el sistema de coordenadas utilizados (con mayor frecuencia cartesiano o polar).
Usando el Cayley-Hamilton teorema que establece que cada matriz cuadrada satisface su propia ecuaci??n caracter??stica, se puede demostrar que (lo m??s generalmente, en el espacio complejo) existe al menos un vector distinto de cero que satisface la ecuaci??n de valores propios para esa matriz. Como se dijo en la secci??n Definiciones, a cada valor propio corresponder un n??mero infinito de colineales vectores propios (linealmente dependientes) que forman el espacio propio para este valor propio. Por otra parte, la dimensi??n del espacio caracter??stico es igual al n??mero de los vectores propios linealmente independientes que contiene. La multiplicidad geom??trica de un valor propio se define como la dimensi??n del espacio caracter??stico asociado. Un valor propio m??ltiple puede dar lugar a un ??nico vector propio de manera que su multiplicidad algebraica puede ser diferente de la multiplicidad geom??trica. Sin embargo, como ya se ha dicho, los diferentes valores propios son emparejados con vectores propios linealmente independientes. De lo anterior, se deduce que la multiplicidad geom??trica no puede ser mayor que la multiplicidad algebraica.
Por ejemplo, un vector propio de una rotaci??n en tres dimensiones es un vector situado dentro de la eje alrededor del cual se realiza la rotaci??n. El valor propio correspondiente es 1 y el espacio caracter??stico correspondiente contiene todos los vectores a lo largo del eje. Como se trata de un espacio unidimensional, su multiplicidad geom??trica es uno. Este es el ??nico valor propio del espectro (de esta rotaci??n) que es un n??mero real .
Ejemplos
Los ejemplos que siguen son para el caso m??s simple de vector de dos dimensiones espacio L 2, pero que pueden ser f??cilmente aplicadas de la misma manera a los espacios de dimensiones superiores.
Homotecia, identidad, punto de reflexi??n y transformaci??n nula
Como un espacio unidimensional vector L 1, considere una cuerda el??stica atada al apoyo inm??vil en uno de los extremos, tales como los de la honda de un ni??o. Tirando de la cuerda de distancia desde el punto de uni??n se extiende y se alarga por alg??n factor de escala λ que es un n??mero real. Cada vector de la cuerda se estira por igual, con el mismo factor de escala λ, y aunque alargado que conserva su direcci??n original. Este tipo de transformaci??n se llama homotecia (transformaci??n de semejanza). Para un espacio vectorial de dos dimensiones L 2, considere una hoja de goma estirada por igual en todas las direcciones como una peque??a ??rea de la superficie de un globo inflado (Fig. 3). Todos los vectores que se originan en un punto fijo en la superficie del globo se estiran igualmente con el mismo factor de escala λ. La transformaci??n homotecia en dos dimensiones es descrito por una matriz cuadrada 2 ?? 2, que act??a sobre un vector arbitrario en el plano de la superficie de estiramiento / contracci??n. Despu??s de hacer la multiplicaci??n de la matriz, se obtiene:
que, expresada en palabras, significa que la transformaci??n es equivalente a multiplicar la longitud del vector λ por preservando al mismo tiempo su direcci??n original. La ecuaci??n obtenida de este modo es exactamente la ecuaci??n de valor propio. Dado que el vector tomada fue arbitraria, en homotecia cualquier vector en el espacio vectorial se somete a la ecuaci??n de valor propio, es decir, cualquier vector acostado en la superficie del globo puede ser un vector propio. Si la transformaci??n es el estiramiento (elongaci??n, la extensi??n, la inflaci??n), o en contracci??n (compresi??n, la deflaci??n) depende del factor de escala: si λ> 1, se est?? estirando, si λ <1, se est?? reduciendo.
Varias otras transformaciones pueden considerarse tipos especiales de homotecia con alg??n valor fijo, constante de λ: en la identidad que deja vectores sin cambios, λ = 1; en la reflexi??n alrededor de un punto que conserva longitud y direcci??n de los vectores pero cambia su orientaci??n al opuesto, λ = -1; y en la transformaci??n nula que transforma cada vector para el vector cero, λ = 0. La transformaci??n nula no da lugar a un vector propio ya que el vector cero no puede ser un vector propio pero ha autoespacio desde el espacio caracter??stico tambi??n contiene el vector cero por definici??n.
Escalado desigual
Para un ejemplo ligeramente m??s complicado, considere una hoja que se estira uneqally en dos direcciones perpendiculares a lo largo de los ejes de coordenadas, o, de manera similar, estirado en una direcci??n, y reducido en la otra direcci??n. En este caso, hay dos factores de escala diferentes: k 1 para la ampliaci??n en la direcci??n x, y k 2 para la ampliaci??n en la direcci??n y. La matriz de transformaci??n es  Y la ecuaci??n caracter??stica es λ 2 - λ (k 1 + k 2) + k 1 k 2 = 0. Los valores propios, obtenido como ra??ces de esta ecuaci??n son λ 1 = k 1 y λ 2 = k 2 lo que significa, como se esperaba, que los dos valores propios son los factores de escala en las dos direcciones. Enchufar k 1 vuelta en la ecuaci??n del valor propio da uno de los vectores propios:
Y la ecuaci??n caracter??stica es λ 2 - λ (k 1 + k 2) + k 1 k 2 = 0. Los valores propios, obtenido como ra??ces de esta ecuaci??n son λ 1 = k 1 y λ 2 = k 2 lo que significa, como se esperaba, que los dos valores propios son los factores de escala en las dos direcciones. Enchufar k 1 vuelta en la ecuaci??n del valor propio da uno de los vectores propios:
Dividiendo la ??ltima ecuaci??n por 2 k - k 1, se obtiene y = 0, que representa el eje x. Un vector con longitud 1 tomada a lo largo de este eje representa el vector propio normalizado correspondiente al valor propio λ 1. El vector propio correspondiente a λ 2, que es un vector unitario a lo largo del eje y se encuentra en una forma similar. En este caso, ambos valores propios son simples (con algebraica y las multiplicidades geom??tricas igual a 1). Dependiendo de los valores de λ 1 y λ 2, hay varios casos especiales notables. En particular, si λ 1> 1, y λ 2 = 1, la transformaci??n es un estiramiento en la direcci??n del eje x. Si λ 2 = 0, y λ 1 = 1, la transformaci??n es una proyecci??n de la superficie L 2 en el eje x, porque todos los vectores en la direcci??n de y se convierten en cero vectores.
Que la l??mina de caucho se estira a lo largo del eje x (k 1> 1) y se redujo de forma simult??nea a lo largo del eje y (k 2 <1) como en la Fig. 4. Entonces λ 1 = k 1 ser?? el valor propio director. Aplicando repetidamente esta transformaci??n de estiramiento / contracci??n muchas veces a la l??mina de goma se haga de esta ??ltima cada vez m??s similar a una cadena de goma. Cualquier vector en la superficie de la l??mina de caucho se orientar?? m??s y m??s cerca a la direcci??n del eje x (la direcci??n de estiramiento), es decir, se convertir?? en colineal con el vector propio director.
Shear
Shear en el plano es una transformaci??n en la que todos los puntos a lo largo de una l??nea dada permanecen fijos mientras que otros puntos se desplazan en paralelo a esa l??nea por una distancia proporcional a su distancia perpendicular desde la l??nea. A diferencia de la escala, la esquila una figura plana no cambia su ??rea. Shear puede ser horizontal - a lo largo del eje X, o vertical - lo largo del eje Y. En cizalladura horizontal (Fig. 5), un punto P del plano se mueve paralelamente al eje X hasta el lugar P 'de modo que su coordenada y no cambia, mientras que la coordenada x para convertirse en incrementos de x' = x + k, donde k se llama factor de cizallamiento. El factor de corte es proporcional a y y al φ ??ngulo de distorsi??n: k = x '- x = y φ cuna. La matriz de una transformaci??n de cizalladura horizontal es  . La ecuaci??n caracter??stica es λ 2 - 2 λ + 1 = (1 - λ) 2 = 0 que tiene una sola ra??z λ = 1. Por lo tanto, el valor propio λ = 1 es m??ltiple con multiplicidad algebraica 2. El vector propio (s) se encuentran como soluciones de
. La ecuaci??n caracter??stica es λ 2 - 2 λ + 1 = (1 - λ) 2 = 0 que tiene una sola ra??z λ = 1. Por lo tanto, el valor propio λ = 1 es m??ltiple con multiplicidad algebraica 2. El vector propio (s) se encuentran como soluciones de
La ??ltima ecuaci??n se divide por k (normalizaci??n) para obtener y = 0 que es una l??nea recta a lo largo del eje x. Esta l??nea representa el espacio caracter??stico unidimensional. En el caso de cizallamiento la multiplicidad algebraica del valor propio (2) es menor que su multiplicidad geom??trica (1, la dimensi??n del espacio caracter??stico). El vector propio es un vector unitario a lo largo del eje x. El caso de la cizalladura vertical con matriz de transformaci??n  se trata en la misma forma; el vector propio en cizalladura vertical es a lo largo del eje y. Aplicando repetidamente la transformaci??n de cizallamiento cambia la direcci??n de cualquier vector en el plano m??s y m??s cerca a la direcci??n del vector propio.
se trata en la misma forma; el vector propio en cizalladura vertical es a lo largo del eje y. Aplicando repetidamente la transformaci??n de cizallamiento cambia la direcci??n de cualquier vector en el plano m??s y m??s cerca a la direcci??n del vector propio.
Rotaci??n

La la rotaci??n en un plano es una transformaci??n que describe el movimiento de un cuerpo r??gido (o vector) alrededor de un punto fijo. Con la ayuda de funciones trigonom??tricas, la rotaci??n puede ser descrito como una transformaci??n lineal. Los elementos de una matriz de rotaci??n representan los componentes del vector girado. As??, una rotaci??n antihoraria de un vector de coordenadas, o plano sobre el origen en un ??ngulo φ con lo que las coordenadas x y el cambio y a x 'e y' es descrito por el siguiente sistema de ecuaciones lineales:
o, en t??rminos de matrices y vectores columna:
La ecuaci??n caracter??stica de la matriz de transformaci??n  es λ 2 - 2λ cos φ + 1 = 0. Esta ecuaci??n cuadr??tica tiene un discriminante D = 4 (cos φ 2 - 1) = - 4 sen φ 2, que es un n??mero negativo para φ ≠ 0 ?? y 180 ?? φ ≠ ?? k con k impar. Por lo tanto, excepto en los casos especiales este ??ltimo, no existen ra??ces reales (valores propios) para la rotaci??n. La ecuaci??n caracter??stica tiene dos ra??ces complejas λ 1 y λ 2 que son complejos conjugados el uno del otro:
es λ 2 - 2λ cos φ + 1 = 0. Esta ecuaci??n cuadr??tica tiene un discriminante D = 4 (cos φ 2 - 1) = - 4 sen φ 2, que es un n??mero negativo para φ ≠ 0 ?? y 180 ?? φ ≠ ?? k con k impar. Por lo tanto, excepto en los casos especiales este ??ltimo, no existen ra??ces reales (valores propios) para la rotaci??n. La ecuaci??n caracter??stica tiene dos ra??ces complejas λ 1 y λ 2 que son complejos conjugados el uno del otro:
Estas dos ra??ces son los dos valores propios de la rotaci??n, cada uno con una multiplicidad algebraica igual a 1. Enchufar el primer valor propio, λ 1, de vuelta en la ecuaci??n del valor propio da el primer vector propio:
Otros ejemplos
Como la Tierra gira, cada flecha que apunta hacia afuera desde el centro de la Tierra también gira, excepto esas flechas que son paralelas al eje de rotación. Considere la posibilidad de la transformación de la Tierra después de una hora de rotación: Una flecha del centro de la Tierra a la geográfica del Polo Sur sería un vector propio de esta transformación, pero una flecha desde el centro de la Tierra a cualquier punto de la línea ecuatorial , no sería un vector propio. Desde la flecha que apunta en el polo no se estira por la rotación de la Tierra, su valor propio es 1.

Sin embargo, el espacio geométrico tridimensional no es el único espacio vectorial. Por ejemplo, considere una cuerda subrayado fija en ambos extremos, como las cuerdas vibrantes de un instrumento de cuerda (Fig. 2). Las distancias de los átomos de la cuerda vibrante de sus posiciones cuando la cuerda está en reposo pueden ser vistos como los componentes de un vector en un espacio con tantas dimensiones como hay átomos en la cuerda.
Suponga que la cuerda es un medio continuo. Si se tiene en cuenta la ecuación de la aceleración en cada punto de la cuerda, sus vectores propios o funciones propias , son las ondas estacionarias. Las ondas estacionarias corresponden a oscilaciones particulares de la cuerda de tal manera que la aceleración de la cuerda es simplemente su forma escalado por un factor de este factor, el valor propio, resulta ser  donde
donde 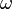 es el la frecuencia angular de la oscilación. Cada componente del vector asociado con la cuerda se multiplica por un factor dependiente del tiempo
es el la frecuencia angular de la oscilación. Cada componente del vector asociado con la cuerda se multiplica por un factor dependiente del tiempo  . Si de amortiguación se considera, la amplitud de esta oscilación disminuye hasta que la cuerda deja de oscilar, correspondiente a un complejo ??. Uno puede entonces asociar toda la vida con la parte imaginaria de ??, y relacionar el concepto de un vector propio para el concepto de resonancia. Sin amortiguación, el hecho de que el operador de aceleración (suponiendo una densidad uniforme) es hermitianos conduce a varias propiedades importantes, tales como que los patrones de ondas de pie son funciones ortogonales.
. Si de amortiguación se considera, la amplitud de esta oscilación disminuye hasta que la cuerda deja de oscilar, correspondiente a un complejo ??. Uno puede entonces asociar toda la vida con la parte imaginaria de ??, y relacionar el concepto de un vector propio para el concepto de resonancia. Sin amortiguación, el hecho de que el operador de aceleración (suponiendo una densidad uniforme) es hermitianos conduce a varias propiedades importantes, tales como que los patrones de ondas de pie son funciones ortogonales.
Funciones propias
Sin embargo, a veces es poco natural o incluso imposible escribir la ecuación de valor propio en forma de matriz. Esto ocurre por ejemplo cuando el espacio vectorial de dimensión infinita es, por ejemplo, en el caso de la cuerda por encima. Dependiendo de la naturaleza de la transformación T y el espacio al que se aplica, puede ser ventajoso para representar la ecuación de valor propio como un conjunto de ecuaciones diferenciales . Si T es un operador diferencial, los vectores propios son comúnmente llamados funciones propias del operador diferencial que representan T . Por ejemplo, diferenciación en sí es una transformación lineal desde
(f(t) yg(t) sonfunciones diferenciables, yunybsonconstantes).
Considere la posibilidad de diferenciación con respecto a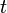 .sus funciones propiash(t) obedecer la ecuación de valor propio:
.sus funciones propiash(t) obedecer la ecuación de valor propio:
 ,
,
donde ?? es el valor propio asociado a la función. Tal función del tiempo es constante si  , crece proporcionalmente a sí mismo, si
, crece proporcionalmente a sí mismo, si 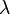 es positivo, y decae proporcionalmente a sí mismo si
es positivo, y decae proporcionalmente a sí mismo si 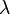 es negativo. Por ejemplo, una población idealizada de conejos engendra más rápido cuanto más conejos hay, y por lo tanto satisface la ecuación con una lambda positivo.
es negativo. Por ejemplo, una población idealizada de conejos engendra más rápido cuanto más conejos hay, y por lo tanto satisface la ecuación con una lambda positivo.
La solución a la ecuación de valor propio es 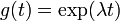 , la función exponencial ; por tanto, que la función es una función propia del operador diferencial d / dt con el valor propio ?? . Si ?? es negativo , que llamamos la evolución de g un decaimiento exponencial; si es positivo , un crecimiento exponencial . El valor de ?? puede ser cualquier número complejo . El espectro de d / dt es por lo tanto todo el plano complejo . En este ejemplo, el espacio vectorial en el que el operador d / dt actúa es el espacio de las funciones diferenciables de una variable. Este espacio tiene una dimensión infinita (porque no es posible expresar cada función diferenciable como una combinación lineal de un número finito de funciones de base). Sin embargo, el espacio característico asociado con cualquier valor propio dado ?? es unidimensional. Es el conjunto de todas las funciones
, la función exponencial ; por tanto, que la función es una función propia del operador diferencial d / dt con el valor propio ?? . Si ?? es negativo , que llamamos la evolución de g un decaimiento exponencial; si es positivo , un crecimiento exponencial . El valor de ?? puede ser cualquier número complejo . El espectro de d / dt es por lo tanto todo el plano complejo . En este ejemplo, el espacio vectorial en el que el operador d / dt actúa es el espacio de las funciones diferenciables de una variable. Este espacio tiene una dimensión infinita (porque no es posible expresar cada función diferenciable como una combinación lineal de un número finito de funciones de base). Sin embargo, el espacio característico asociado con cualquier valor propio dado ?? es unidimensional. Es el conjunto de todas las funciones  , donde A es una constante arbitraria, la población inicial en t = 0 .
, donde A es una constante arbitraria, la población inicial en t = 0 .
Teorema Espectral
En su versión más simple, el teorema espectrales que, bajo ciertas condiciones, una transformación lineal de un vector v se puede expresar como una combinación lineal de los vectores propios, en la que el coeficiente de cada vector propio es igual a los tiempos de valores propios correspondientes el producto escalar (o producto punto) del vector propio con el vector v . Matemáticamente, se puede escribir como:
donde v 1 , v 2 , ... y ?? 1 , ?? 2 , ... presentarse a los vectores propios y valores propios de T . El teorema es válido para todas las transformaciones lineales autoadjuntos (transformaciones lineales dadas por verdaderas matrices simétricas y matrices hermitianas), y para la clase más general de ( complejos ) matrices normales.
Si se define la n -ésima potencia de una transformación como el resultado de aplicar que n veces en sucesión, también se puede definir polinomios de transformaciones. Una versión más general del teorema es que cualquier polinomio P de T está dada por
El teorema se puede extender a otras funciones de transformaciones, comolas funciones analíticas, el caso más general de serfunciones de Borel.
Eigendecomposition
La teorema espectral para matrices puede enunciarse como sigue. Vamos A ser un cuadrado n × n matriz. Deje q 1 ... q k sea una base vector propio, es decir, un conjunto indexado de k vectores propios linealmente independientes, donde k es la dimensión del espacio abarcado por los vectores propios de A . Si k = n , entonces A puede escribirse
dondeQes el cuadradon×nmatriz cuyai-ésima columna es el vector propio baseq yodeAy??es lamatriz diagonal cuyos elementos diagonales son los valores propios correspondientes, es decir,?? ii= ??yo.
Espacios de dimensión infinita
Si el espacio vectorial es una dimensión infinita espacio de Banach, la noción de valores propios se puede generalizar el concepto de espectro. El espectro es el conjunto de escalares ?? para los que ( T - ??) -1 no está definido; es decir, tal que T - ?? no tiene inversa acotada.
Es evidente que si ?? es un valor propio de T , ?? es en el espectro de T . En general, lo contrario no es cierto. Hay operadores de Hilbert o espacios de Banach que no tienen vectores propios en absoluto. Esto se puede ver en el siguiente ejemplo. La cambio bilateral en el espacio de Hilbert ??? 2 ( Z ) (es decir, el espacio de todas las secuencias de escalares ... un -1 , un 0 , un 1 , una 2 , ... de tal manera que
converge) no tiene valor propio, pero tiene valores espectrales.
En los espacios infinito-dimensionales, el espectro de un operador acotado siempre es no vacío. Esto también es válido para una ilimitada operador auto adjunto. A través de sus medidas espectrales, el espectro de cualquier operador auto adjunto, delimitadas o no, se puede descomponer en el punto absolutamente continua, puro y piezas singulares. (Ver Descomposición del espectro.)
Las funciones exponenciales son funciones propias del operador de la derivada (la derivada de funciones exponenciales son proporcionales a sí mismos). El crecimiento exponencial y decaimiento por lo tanto, proporcionan ejemplos de espectros continuos, como lo hace el ejemplo cuerda vibrante ilustrado anteriormente. La átomo de hidrógeno es un ejemplo donde ambos tipos de espectros aparecerá. Las funciones propias del hamiltoniano átomo de hidrógeno se llaman estados propios y se agrupan en dos categorías. La estados ligados del átomo de hidrógeno corresponder a la parte discreta del espectro (tienen un conjunto discreto de valores propios que puede ser calculada por la fórmula de Rydberg) mientras que la ionización procesos se describen por la parte continua (la energía de la colisión / ionización no se cuantifica).
Aplicaciones
Ecuación de Schrödinger

Un ejemplo de una ecuación de autovalores donde la transformaciónTse representa en términos de un operador diferencial es independiente del tiempo de laecuación de Schrödinger enla mecánica cuántica:
dondeH, elhamiltoniano, es una de segundo ordenoperador diferencial y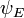 , La función de onda, es una de sus funciones propias correspondientes al valor propioE, interpretadas como suenergía.
, La función de onda, es una de sus funciones propias correspondientes al valor propioE, interpretadas como suenergía.
Sin embargo, en el caso en que uno está interesado sólo en las soluciones estatales encuadernadas de la ecuación de Schrödinger, uno busca 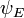 en el espacio de funciones integrables cuadradas. Desde este espacio es un espacio de Hilbert con una bien definida producto escalar, se puede introducir una base conjunto en el que
en el espacio de funciones integrables cuadradas. Desde este espacio es un espacio de Hilbert con una bien definida producto escalar, se puede introducir una base conjunto en el que 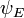 y H se puede representar como una matriz unidimensional y una matriz, respectivamente. Esto le permite a uno representan la ecuación de Schrödinger en forma de matriz. (Fig. 4 presenta las funciones propias bajas del hamiltoniano átomo de hidrógeno.)
y H se puede representar como una matriz unidimensional y una matriz, respectivamente. Esto le permite a uno representan la ecuación de Schrödinger en forma de matriz. (Fig. 4 presenta las funciones propias bajas del hamiltoniano átomo de hidrógeno.)
La Notación de Dirac se utiliza a menudo en este contexto. Un vector, que representa un estado del sistema, en el espacio de Hilbert de funciones integrables cuadrados está representado por  . En esta notación, la ecuación de Schrödinger es:
. En esta notación, la ecuación de Schrödinger es:
donde  es un estado propio de H . Es un operador auto adjunto, el análogo tridimensional infinita de matrices hermitianas ( ver observable ). Como en el caso de la matriz, en la ecuación anterior
es un estado propio de H . Es un operador auto adjunto, el análogo tridimensional infinita de matrices hermitianas ( ver observable ). Como en el caso de la matriz, en la ecuación anterior  se entiende que es el vector obtenido mediante la aplicación de la transformación H de
se entiende que es el vector obtenido mediante la aplicación de la transformación H de  .
.
Orbitales moleculares
En la mecánica cuántica , y en particular en atómica y la física molecular , dentro de la teoría de Hartree-Fock, los at??mico y orbitales moleculares pueden ser definidas por los vectores propios de la operador de Fock. Los valores propios correspondientes se interpretan como potenciales de ionización a través teorema de Koopmans. En este caso, el término vector propio se utiliza en un significado algo más general, ya que el operador de Fock depende explícitamente en los orbitales y sus valores propios. Si uno quiere subrayar este aspecto se habla de la ecuación de valores propios implícita . Tales ecuaciones se resuelven generalmente por un procedimiento de iteración, llamado en este caso método de campo autoconsistente. En la química cuántica , a menudo se representa la ecuación de Hartree-Fock en un no- ortogonal base fija. Esta representación en particular es un problema de valores propios generalizado llamado ecuaciones Roothaan.
Geología y Glaciología: (Tensor Orientación)
En geología , especialmente en el estudio de glacial hasta, vectores propios y valores propios se utilizan como un método por el cual una masa de información de la orientación y la inmersión constituyentes de una tela clast 'se puede resumir en un espacio 3-D por seis números. En el campo, un geólogo puede recopilar tales datos para cientos o miles de clastos en una muestra de suelo, que sólo se pueden comparar gráficamente como en un Tri-Plot (Sneed y Folk) diagrama, o como stereonet en un Wulff Net . La salida para el tensor de orientación es en los tres (perpendicular) ejes ortogonales del espacio. Salida de vectores propios de programas como Stereo32 están en el orden E1> E2> E3, con E1 ser la orientación principal de clast orientación / inmersión, E2 siendo la secundaria y E3 es el terciario, en términos de fuerza. La orientación clast se define como el vector propio, en una rosa de los vientos de 360 °. Dip se mide como el valor propio, el módulo de la tensor: esta se valora de 0 ° (sin DIP) a 90 ° (vertical). Varios valores de E1, E2 y E3 significan cosas diferentes, como se puede ver en el libro 'Una guía práctica para el Estudio de los sedimentos glaciales' por Benn & Evans, 2004.
Análisis factorial
En análisis factorial, los vectores propios de una matriz de covarianza o matriz de correlación corresponden a factores y valores propios de la varianza explicada por estos factores. El análisis factorial es una estadística técnica utilizada en las ciencias sociales y en la marketing, gestión de productos, investigación de operaciones , y otras ciencias aplicadas que se ocupan de grandes cantidades de datos. El objetivo es explicar la mayor parte de la covariabilidad entre un número de observables variables aleatorias en términos de un menor número de variables latentes no observables llamados factores. Las variables aleatorias observables se modelan como combinaciones lineales de los factores, además de los términos de la varianza únicas. Valores propios se utilizan en el análisis utilizado por el software de Q-metodología; factores con valores propios superiores a 1,00 se consideran significativos, explicando una cantidad importante de la variabilidad de los datos, mientras que los valores propios de menos de 1,00 se consideran demasiado débil, no explicar una porción significativa de la variabilidad de los datos.
Eigenfaces
En procesamiento de imágenes, las imágenes procesadas de caras puede ser visto como vectores cuyos componentes son los brillos de cada pixel. La dimensión de este espacio vectorial es el número de píxeles. Los vectores propios de la matriz de covarianza asociada a un gran conjunto de imágenes normalizadas de caras se llaman Eigenfaces; este es un ejemplo de análisis de componentes principales. Son muy útiles para expresar cualquier imagen de la cara como una combinación lineal de algunos de ellos. En el rama de reconocimiento facial de la biometría, Eigenfaces proporcionan un medio para aplicar la compresión de datos de rostros para propósitos de identificación. También se ha hecho la investigación relacionada con los sistemas de visión eigen determinantes gestos con las manos. Más sobre la determinación de las letras de lengua de signos que utilizan eigen sistemas se puede encontrar aquí: http://www.geigel.com/signlanguage/index.php
Similar a este concepto, eigenvoices concepto también se desarrolló lo que representa la dirección general de la variabilidad en las pronunciaciones humanos de una expresión particular, tal como una palabra en un idioma. Basado en una combinación lineal de dichos eigenvoices, una nueva pronunciación de voz de la palabra puede ser construido. Estos conceptos se han encontrado útiles en los sistemas de reconocimiento automático del habla, para la adaptación del altavoz.
Tensor de inercia
En mecánica, los vectores propios de latensor de inercia definen losejes principales de uncuerpo rígido. La tensor de inercia es una cantidad clave requerida con el fin de determinar la rotación de un cuerpo rígido alrededor de sucentro de masa.
Tensor de tensiones
En mecánica de sólidos, el tensor de tensiones es simétrica y por lo tanto se puede descomponer en un tensor diagonal con los valores propios de la diagonal y los vectores propios como base. Debido a que es diagonal, en esta orientación, el tensor de tensiones no tiene componentes de cizallamiento; los componentes que sí tiene son los componentes principales.
Valores propios de una gráfica
En la teoría de grafos espectral, un valor propio de un gráfico se define como un valor propio de del gráfico matriz de adyacencia A , o (cada vez) de de la gráfica de la matriz laplaciana, que es o bien T - A o I - T 1/2 AT -1/2 , donde T es un holding matriz diagonal el grado de cada vértice, y en T -1/2 , 0 es sustituido por 0 -1/2 . El k TH vector propio principal de un gráfico se define como el vector propio correspondiente a la k TH valor propio más grande de A , o el vector propio correspondiente a la k TH valor propio más pequeña del Laplaciano. La primera vector propio principal de la gráfica también se conoce simplemente como el principal vector propio.
El principal vector propio se utiliza para medir la centralidad de sus vértices. Un ejemplo es Google 's algoritmo de PageRank. El director vector propio de un modificado matriz de adyacencia del grafo World Wide Web da las filas de la página como sus componentes. Este vector corresponde a la distribución estacionaria de la cadena de Markov representado por la matriz de adyacencia normalizado fila-; sin embargo, la matriz de adyacencia primero debe ser modificado para asegurar que existe una distribución estacionaria. El segundo vector propio principal puede ser utilizado para dividir el gráfico en grupos, a través de la agrupación espectral. Otros métodos también están disponibles para el agrupamiento.



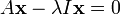




![\ Lambda_ {1,2} = \ frac {1} {2} \ left [(a_ {11} + a_ {22}) \ pm \ sqrt {{12} 4a_ a_ {21} + (a_ {11} - a_ {22}) ^ 2} \ right].](../../images/149/14952.png)