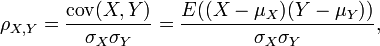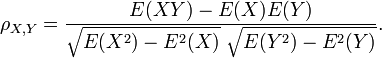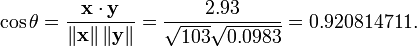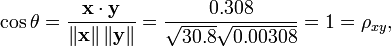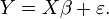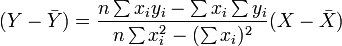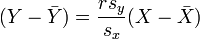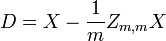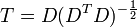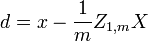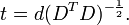Correlaci??n

Temas relacionados: Matem??ticas

Sab??as ...

SOS cree que la educaci??n da una mejor oportunidad en la vida para los ni??os en el mundo en desarrollo tambi??n. El patrocinio de los ni??os ayuda a los ni??os en el mundo en desarrollo para aprender tambi??n.

Este art??culo es sobre el coeficiente de correlaci??n entre dos variables. El t??rmino correlaci??n tambi??n puede significar la correlaci??n cruzada de dos funciones o correlaci??n de electrones en los sistemas moleculares.

Varios conjuntos de (x, y) puntos, con el coeficiente de correlaci??n de x e y para cada conjunto. Tenga en cuenta que la correlaci??n refleja la ruidosidad y la direcci??n de una relaci??n lineal (fila superior), pero no la pendiente de que la relaci??n (en el centro), ni muchos aspectos de las relaciones no lineales (abajo). NB: la figura en el centro tiene una pendiente de 0 pero en ese caso el coeficiente de correlaci??n es indefinido debido a que la varianza de Y es cero.

En teor??a de la probabilidad y estad??sticas , correlaci??n, (a menudo medido como un coeficiente de correlaci??n), indica la fuerza y la direcci??n de una relaci??n lineal entre dos variables aleatorias . En el uso estad??stico general, la correlaci??n o co-relaci??n se refiere a la salida de dos variables de la independencia. En este sentido amplio hay varios coeficientes, que miden el grado de correlaci??n, adaptado a la naturaleza de los datos.

Un n??mero de diferentes coeficientes se utilizan para diferentes situaciones. El m??s conocido es el Pearson coeficiente de correlaci??n momento-producto, que se obtiene dividiendo el covarianza de las dos variables por el producto de sus desviaciones est??ndar . A pesar de su nombre, que se introdujo por primera vez por Francis Galton.

Coeficiente producto-momento de Pearson

Propiedades matem??ticas

El coeficiente de correlaci??n ρ _{X, Y} entre dos variables aleatorias X e Y con valores esperados μ _X y μ _Y y desviaciones est??ndar σ _X y σ _Y se define como:

$\ Rho_ {X, Y} = {\ mathrm {cov} (X, Y) \ over \ sigma_X \ sigma_Y} = {E ((X- \ mu_X) (Y- \ mu_Y)) \ over \ sigma_X \ sigma_Y} ,$

donde E es el operador valor esperado y cov medios covarianza. Desde μ _X = E (X), _X σ ² = E (X ²⁾ - E ² (X) y del mismo modo para Y, podemos escribir tambi??n

$\ Rho_ {X, Y} = \ frac {E (XY) -S (X) E (Y)} {\ sqrt {E (X ^ 2) -E ^ 2 (X)} ~ \ sqrt {E (Y ^ 2) -E ^ 2 (Y)}}.$

La correlaci??n se define s??lo si tanto de las desviaciones est??ndar son finitos y dos de ellos son no cero. Es un corolario de la desigualdad de Cauchy-Schwarz que la correlaci??n no puede exceder de 1 en valor absoluto .

La correlaci??n es 1 en el caso de una relaci??n lineal creciente, -1 en el caso de una relaci??n lineal decreciente, y en alg??n valor entre en todos los dem??s casos, lo que indica el grado de dependencia lineal entre las variables. Cuanto m??s cerca el coeficiente es o bien -1 o 1, m??s fuerte ser?? la correlaci??n entre las variables.

Si las variables est??n entonces independiente de la correlaci??n es 0, pero lo contrario no es cierto porque el coeficiente de correlaci??n s??lo detecta dependencias lineales entre dos variables. He aqu?? un ejemplo: Supongamos que la variable aleatoria X se distribuye uniformemente en el intervalo de -1 a 1, e Y = X ^2. Entonces Y es completamente determinado por X, de manera que X e Y son dependientes, pero su correlaci??n es cero; son correlacionadas. Sin embargo, en el caso especial cuando X e Y son conjuntamente normal, uncorrelatedness es equivalente a la independencia.

Una correlaci??n entre dos variables se diluye en la presencia de un error de medici??n alrededor de las estimaciones de uno o de ambas variables, en cuyo caso disattenuation proporciona un coeficiente m??s precisa.

Interpretaci??n geom??trica de correlaci??n

El coeficiente de correlaci??n tambi??n se puede ver como el coseno del ??ngulo entre los dos vectores de muestras extra??das de las dos variables aleatorias.

Precauci??n: Este m??todo s??lo funciona con los datos de centrado, es decir, los datos que han sido desplazadas por la media de la muestra de manera que tenga un promedio de cero. Algunos m??dicos prefieren un uncentered (no Pearson conforme) coeficiente de correlaci??n. Vea el siguiente ejemplo para una comparaci??n.

A modo de ejemplo, supongamos que cinco pa??ses se encuentran para tener productos nacionales brutos de 1, 2, 3, 5 y 8 mil millones de d??lares, respectivamente. Supongamos que estos mismos cinco pa??ses (en el mismo orden) se encontr?? que ten??a un 11%, 12%, 13%, 15% y 18% de pobreza. Entonces Sean X e Y pueden pedir vectores 5 elementos que contienen los datos anteriores: x = (1, 2, 3, 5, 8) ey = (0,11, 0,12, 0,13, 0,15, 0,18).

Por el procedimiento habitual para encontrar el ??ngulo entre dos vectores (ver dot producto), el coeficiente de correlaci??n uncentered es:

$\ Cos \ theta = \ frac {\ bold {x} \ cdot \ bold {y}} {\ left \ | \ bold {x} \ right \ | \ left \ | \ bold {y} \ right \ |} = \ frac {2,93} {\ sqrt {103} \ sqrt {0,0983}} = 0,920814711.$

Tenga en cuenta que los datos anteriores fueron elegidos deliberadamente para ser perfectamente correlacionados: y = 0,10 + 0,01 x. Por tanto, el coeficiente de correlaci??n de Pearson debe ser exactamente una. Centrado de los datos (por desplazamiento x E (x) = 3,8 e y por E (y) = 0,138) los rendimientos x = (-2.8, -1.8, -0.8, 1.2, 4.2) y y = (-0,028, -0,018, -0,008, 0,012, 0,042), de la cual

$\ Cos \ theta = \ frac {\ bold {x} \ cdot \ bold {y}} {\ left \ | \ bold {x} \ right \ | \ left \ | \ bold {y} \ right \ |} = \ frac {0,308} {\ sqrt {30.8} \ sqrt {0,00308}} = 1 = \ rho_ {xy},$

como se esperaba.

La motivaci??n para la forma del coeficiente de correlaci??n

Otra motivaci??n para la correlaci??n viene de inspeccionar el m??todo simple de regresi??n lineal . Como anteriormente, X es el vector de variables independientes, 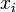$x_i$ , E Y de las variables dependientes, 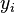$y_i$ , Y una relaci??n lineal simple entre X e Y se busca, a trav??s de un m??todo de m??nimos cuadrados en la estimaci??n de Y:

$\ Y = X \ beta + \ varepsilon. \,$

Entonces, la ecuaci??n de la recta de m??nimos cuadrados se puede derivar a ser de la forma:

$(Y - \ bar {Y}) = \ frac {n \ suma x_iy_i- \ suma x_i \ suma y_i} {n \ suma x_i ^ 2 - (\ sum x_i) ^ 2} (X - \ bar {X})$

que se puede variar la forma:

$(Y - \ bar {Y}) = \ frac {r} {s_y s_x} (X \ bar {X})$

donde r tiene la forma familiar se ha mencionado anteriormente: 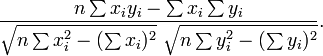$\ Frac {n \ suma x_iy_i- \ suma x_i \ suma y_i} {\ sqrt {n \ suma x_i ^ 2 - (\ sum x_i) ^ 2} ~ \ sqrt {n \ suma y_i ^ 2 - (\ sum y_i) ^ 2}}.$

Interpretaci??n del tama??o de una correlaci??n

Correlaci??n	Negativo	Positivo
Peque??o	-0,3--0,1	0,1 a 0,3
Medio	-0,5 Y -0,3	0,3 a 0,5
Grande	-1,0--0,5	0,5 a 1,0

Varios autores han ofrecido directrices para la interpretaci??n de un coeficiente de correlaci??n. Cohen (1988), por ejemplo, ha sugerido las siguientes interpretaciones de correlaciones en la investigaci??n psicol??gica, en la tabla de la derecha.

Como el propio Cohen ha observado, sin embargo, todos esos criterios son en cierta forma arbitraria y no deben ser observados de manera demasiado estricta. Esto es debido a que la interpretaci??n de un coeficiente de correlaci??n depende del contexto y prop??sitos. Una correlaci??n de 0,9 puede ser muy bajos si se est?? verificando una ley f??sica utilizando instrumentos de alta calidad, sino que puede ser considerado como muy alto en las ciencias sociales donde puede haber una mayor contribuci??n de factores de complicaci??n.

A lo largo de este orden de ideas, es importante recordar que los "grandes" y "peque??os" no debe tomarse como sin??nimos de "bueno" y "malo" en cuanto a la determinaci??n de que una correlaci??n es de un tama??o determinado. Por ejemplo, una correlaci??n de 1,0 o -1,0 indica que las dos variables analizadas son de escala de m??dulo equivalente. Cient??ficamente, esto indica m??s frecuentemente consecuencia trivial de una estremecedora uno. Por ejemplo, considere la posibilidad de descubrir una correlaci??n de 1,0 entre cu??ntos pies de altura a un grupo de personas son y el n??mero de pulgadas de la parte inferior de los pies a la parte superior de sus cabezas.

Coeficientes de correlaci??n no param??tricas

Coeficiente de correlaci??n de Pearson es un estad??stica param??trica y cuando las distribuciones no son normales, puede ser menos ??til que m??todos de correlaci??n no param??tricos, tales como Chi-cuadrado, Apunte correlaci??n biserial, Ρ de Spearman y Τ de Kendall. Son un poco menos potente que los m??todos param??tricos si se dan los supuestos que subyacen a la ??ltima, pero tienen menos probabilidades de dar resultados distorsionados cuando los supuestos no se cumplen.

Otras medidas de la dependencia entre variables aleatorias

Para obtener una medida para las dependencias m??s generales en los datos (tambi??n no lineal) es mejor utilizar el relaci??n de correlaci??n que es capaz de detectar casi cualquier dependencia funcional, o la basado entrop??a- informaci??n mutua / correlaci??n total que es capaz de detectar incluso dependencias m??s generales. Estos ??ltimos se denominan a veces como medidas de correlaci??n m??ltiple momento, en comparaci??n con aquellos que consideran s??lo segundo momento (por parejas o cuadr??tica) dependencia.

La correlaci??n polic??rica es otra correlaci??n aplicado a los datos ordinal que tiene como objetivo estimar la correlaci??n entre las variables latentes teorizadas.

Las c??pulas y correlaci??n

La informaci??n dada por un coeficiente de correlaci??n no es suficiente para definir la estructura de dependencia entre variables aleatorias; para captar plenamente lo debemos tener en cuenta una c??pula entre ellos. El coeficiente de correlaci??n define completamente la estructura de dependencia s??lo en casos muy particulares, por ejemplo cuando el funciones de distribuci??n acumulada son los distribuciones normales multivariantes. En el caso de distribuciones el??pticas caracteriza la (hiper) elipses de igual densidad, sin embargo, no caracteriza completamente la estructura de dependencia (por ejemplo, grados la una multivariante de t-distribuci??n de la libertad de determinar el nivel de dependencia de la cola).

Matrices de correlaci??n

La matriz de correlaci??n de n variables aleatorias X _1, ..., X _n es la matriz n ?? n cuyos i, j entrada es corr (X _{i, j} X). Si las medidas de correlaci??n utilizados son coeficientes momento-producto, la matriz de correlaci??n es la misma que la matriz de covarianza de las variables aleatorias estandarizados X _i / SD (X _i) para i = 1, ..., n. En consecuencia, es necesariamente una matriz positiva semidefinida.

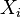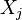La matriz de correlaci??n es sim??trica porque la correlaci??n entre $X_i$ y $X_j$ es la misma que la correlaci??n entre 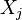$X_j$ y $X_i$ .

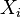Extracci??n de correlaci??n

Siempre es posible eliminar la correlaci??n entre variables aleatorias con media cero con una transformaci??n lineal, incluso si la relaci??n entre las variables no es lineal. Supongamos que un vector de n variables aleatorias se muestrea m veces. Sea X una matriz en la que 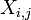$X_ {i, j}$ es la j-??sima variable de la muestra i. Dejar 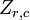$Z_ {r, c}$ ser un r por c matriz con todos los elementos 1. Entonces D es los datos transformados por lo que cada variable aleatoria tiene media cero y T son los datos transformados por lo que todas las variables tienen media cero, varianza unidad y correlaci??n cero con todas las dem??s variables. Las variables transformadas ser??n correlacionadas, a pesar de que no pueden ser independiente.

$D = X - \ frac {1} {m} Z_ {m, m} X$

$T = D (D ^ T D) ^ {- \ frac {1} {2}}$

donde un exponente de -1/2 representa la ra??z cuadrada de la matriz inversa de una matriz. La matriz de covarianza de T ser?? la matriz de identidad. Si una nueva muestra de datos x es un vector fila de n elementos, entonces el mismo transformar se puede aplicar a x para obtener los vectores transformados d y t:

$d = x - \ frac {1} {m} Z_ {1, m} X$

$t = d (D ^ T D) ^ {- \ frac {1} {2}}.$

Conceptos err??neos comunes sobre la correlaci??n

Correlaci??n y causalidad

La m??xima convencional de que " La correlaci??n no implica causalidad "significa que la correlaci??n no puede utilizarse v??lidamente para inferir una relaci??n causal entre las variables. Este dictamen no debe entenderse en el sentido de que las correlaciones no pueden indicar las relaciones causales. Sin embargo, las causas subyacentes de la correlaci??n, en su caso, puede ser indirecta y desconocido. En consecuencia, el establecimiento de una correlaci??n entre dos variables no es una condici??n suficiente para establecer una relaci??n causal (en cualquier direcci??n).

Aqu?? est?? un ejemplo sencillo: el clima caliente puede causar tanto las compras de criminalidad y de helados. Por lo tanto el crimen est?? relacionado con las compras de helados. Pero el crimen no causa compras de helado y las compras de helados no causan crimen.

Una correlaci??n entre la edad y talla de los ni??os es bastante causalmente transparente, pero una correlaci??n entre el estado de ??nimo y la salud en las personas es menos. ??El mejor estado de ??nimo de plomo a una mejor salud? ??O es que buena ventaja para la salud de buen humor? ??O es que alg??n otro factor subyacen tanto? ??O es pura coincidencia? En otras palabras, una correlaci??n puede ser tomada como evidencia de una posible relaci??n causal, pero no puede indicar cu??l es la relaci??n causal, en su caso, podr??a ser.

Correlaci??n y linealidad

Cuatro conjuntos de datos con la misma correlaci??n de 0,81

Aunque la correlaci??n de Pearson indica la intensidad de una relaci??n lineal entre dos variables, su valor por s?? sola no puede ser suficiente para evaluar esta relaci??n, especialmente en el caso en el supuesto de normalidad es incorrecta.

La imagen de la derecha muestra diagramas de dispersi??n de Cuarteto de Anscombe, un conjunto de cuatro pares diferentes de variables creadas por Francis Anscombe. El cuatro 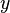$y$ variables tienen la misma media (7,5), la desviaci??n est??ndar (4.12), la correlaci??n (0,81) y la l??nea de regresi??n ( 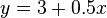$y = 3 + 0.5x$ ). Sin embargo, como puede verse en las parcelas, la distribuci??n de las variables es muy diferente. La primera (arriba a la izquierda) parece que se distribuye normalmente, y corresponde a lo que cabr??a esperar cuando se consideran dos variables correlacionadas y siguiendo el supuesto de normalidad. El segundo (arriba a la derecha) no se distribuye normalmente; mientras que una relaci??n obvia entre las dos variables se puede observar, no es lineal, y el coeficiente de correlaci??n de Pearson no es relevante. En el tercer caso (abajo a la izquierda), la relaci??n lineal es perfecta, a excepci??n de uno outlier que ejerce influencia suficiente para reducir el coeficiente de correlaci??n de 1 a 0,81. Finalmente, el cuarto ejemplo (parte inferior derecha) muestra otro ejemplo, cuando un valor at??pico es suficiente para producir un coeficiente de correlaci??n alta, a pesar de que la relaci??n entre las dos variables no es lineal.

Estos ejemplos indican que el coeficiente de correlaci??n, como una estad??stica de resumen, no puede sustituir el examen individual de los datos.

C??lculo de correlaci??n con precisi??n en una sola pasada

El siguiente algoritmo (en pseudoc??digo) calcular?? Correlaci??n de Pearson con buena estabilidad num??rica.

 sum_sq_x = 0 sum_sq_y = 0 = 0 sum_coproduct mean_x = x [1] mean_y = y [1] para i en 2 a N: barrido = (i - 1,0) / i delta_x = x [i] - mean_x delta_y = y [i ] - mean_y sum_sq_x + = delta_x * * delta_x barrido sum_sq_y + = delta_y * delta_y * sum_coproduct barrido + = delta_x * * delta_y barrido mean_x + = delta_x / i mean_y + = delta_y / i pop_sd_x = sqrt (sum_sq_x / N) pop_sd_y = sqrt (sum_sq_y / N) cov_x_y = sum_coproduct / N correlaci??n = cov_x_y / (pop_sd_x * pop_sd_y)

Recuperado de " http://en.wikipedia.org/w/index.php?title=Correlation_and_dependence&oldid=199055311 "