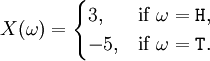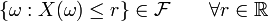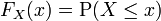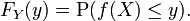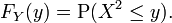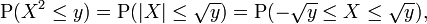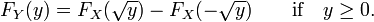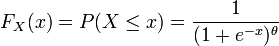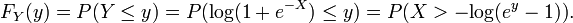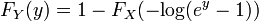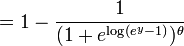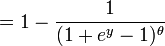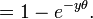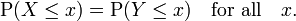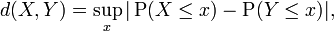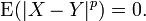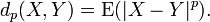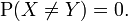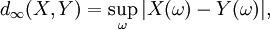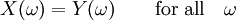Variable aleatoria

Temas relacionados: Matemáticas

Acerca de este escuelas selección Wikipedia

SOS cree que la educación da una mejor oportunidad en la vida para los niños en el mundo en desarrollo también. Para comparar obras de caridad de patrocinio este es el mejor vínculo de patrocinio .

Una variable aleatoria es una abstracción del concepto intuitivo de oportunidad en los dominios teóricos de las matemáticas, la formación de los fundamentos de la teoría de probabilidades y estadística matemática.

La teoría y el lenguaje de variables aleatorias se formalizaron durante los últimos siglos junto a las ideas de la probabilidad. Familiaridad completa con todas las propiedades de variables aleatorias requiere una sólida formación en los conceptos de desarrollo más reciente de teoría de la medida, pero las variables aleatorias se pueden entender de manera intuitiva en varios niveles de fluidez matemática; la teoría de conjuntos y el cálculo son los fundamentales.

En términos generales, una variable aleatoria se define como una cantidad cuyos valores son al azar y en que una distribución de probabilidad se asigna. Más formalmente, una variable aleatoria es una función medible de una espacio de muestra a la espacio medible de posibles valores de la variable. La definición formal de variables aleatorias coloca experimentos con firmeza los resultados de valor real en el medir teórico-marco y nos permite construir las funciones de distribución de variables aleatorias con valores reales.

Ejemplos

Una variable aleatoria se puede utilizar para describir el proceso de laminación una feria morir y los posibles resultados {1, 2, 3, 4, 5, 6}. La representación más obvia es tomar este conjunto como el espacio de muestra, la medida de probabilidad para ser medida uniforme, y la función de ser el función identidad.

Para tirar una moneda, un espacio adecuado de resultados posibles es Ω = {H, T} (para cabezas y colas). Un ejemplo variable aleatoria en este espacio es

$X (\ omega) = \ begin {casos} 3, y \ text {if} \ omega = \ texttt {H}, \\ -5, y \ text {if} \ omega = \ texttt {T}. \ End {casos}$

Variables aleatorias reales con valores

Por lo general, el espacio medible es el espacio medible en los números reales. En este caso, vamos a 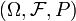$(\ Omega, \ mathcal {F}, P)$ ser un espacio de probabilidad . Entonces, la función de 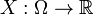$X: \ Omega \ rightarrow \ mathbb {R}$ es una variable aleatoria valor real-si

$\ {\ Omega: X (\ omega) \ le r \} \ in \ mathcal {F} \ qquad \ forall r \ in \ mathbb {R}$

Las funciones de distribución de variables aleatorias

Asociación de una función de distribución acumulativa (CDF) con una variable aleatoria es una generalización de la asignación de un valor a una variable. Si el CDF es una (continua a la derecha) Función de paso Heaviside entonces la variable toma el valor en el salto con probabilidad 1. En general, la CDF especifica la probabilidad de que la variable toma valores particulares.

Si una variable aleatoria 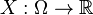$X: \ Omega \ a \ mathbb {R}$ definida en el espacio de probabilidad 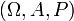$(\ Omega, A, P)$ es dado, podemos hacer preguntas como "¿Qué probabilidades hay de que el valor de 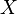$X$ es más grande que 2? ". Esta es la misma que la probabilidad del evento 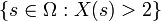$\ {S \ in \ Omega: X (s)> 2 \}$ que a menudo se escribe como 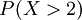$P (X> 2)$ para abreviar.

Grabación de todas estas probabilidades de rangos de salida de un de valor real variable aleatoria X se obtiene la distribución de probabilidad de X. La distribución de probabilidad "olvida" del espacio de probabilidad particular, utilizan para definir X y sólo registra las probabilidades de diversos valores de X. Tal una distribución de probabilidad siempre puede ser capturado por su función de distribución acumulativa

$F_X (x) = \ operatorname {P} (X \ le x)$

y, a veces también utilizando una función de densidad de probabilidad. En términos medir-teórico, utilizamos la variable aleatoria X para "empujar hacia adelante" la medida P en Ω con una medida d F a I. El subyacente Ω espacio de probabilidad es un dispositivo técnico utilizado para garantizar la existencia de variables aleatorias, ya veces para construirlas. En la práctica, se dispone a menudo de la Ω el espacio por completo y sólo pone una medida en R que asigna la medida 1 de toda la recta real, es decir, se trabaja con distribuciones de probabilidad en lugar de variables aleatorias.

Momentos

La distribución de probabilidad de una variable aleatoria a menudo se caracteriza por un pequeño número de parámetros, que también tiene una interpretación práctica. Por ejemplo, a menudo es suficiente para saber cuál es su "valor medio" es. Esto es capturado por el concepto matemático de valor esperado de una variable aleatoria, denotado E [X]. En general, E [f (X)] no es igual a f (E [X]). Una vez que el "valor medio" es conocido, se podría entonces preguntar cómo lejos de este valor medio de los valores de X son típicamente, una pregunta que se responde por la varianza y la desviación típica de una variable aleatoria.

Matemáticamente, esto se conoce como la (generalizada) problema de momentos: para una determinada clase de variables aleatorias X, encontrará una colección {f _i} de funciones tales que la expectativa valora E [f _i (X)] caracterizar completamente la distribución de la variable aleatoria X.

Funciones de variables aleatorias

Si tenemos una variable aleatoria X en Ω y un función medible f: R → R, entonces Y = f (X) también será una variable aleatoria en Ω, ya que la composición de funciones medibles también es mensurable. El mismo procedimiento que permitía uno para ir de un espacio de probabilidad (Ω, P) de (R, dF _X) se puede utilizar para obtener la distribución de Y. La función de distribución acumulativa de Y es

$F_Y (y) = \ operatorname {P} (f (X) \ le y).$

Ejemplo 1

Sea X una de valor real, variable aleatoria continua y dejar Y = X ^2. Luego,

$F_Y (y) = \ operatorname {P} (X ^ 2 \ le y).$

Si y <0, entonces P (X ≤ ² y) = 0, por lo

$F_Y (y) = 0 \ qquad \ hbox {if} \ quad y <0.$

Si y ≥ 0,

$\ Operatorname {P} (X ^ 2 \ le y) = \ operatorname {P} (| X | \ le \ sqrt {y}) = \ operatorname {P} (- \ sqrt {y} \ le x \ le \ sqrt {y}),$

así

$F_Y (y) = F_X (\ sqrt {y}) - F_X (- \ sqrt {y}) \ qquad \ hbox {if} \ quad y \ ge 0.$

Ejemplo 2

Suponer 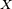$\ Scriptstyle X$ es una variable aleatoria con una distribución acumulativa

$F_ {X} (x) = P (X \ leq x) = \ frac {1} {(1 + e ^ {- x}) ^ {\ theta}}$

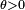donde $\ Scriptstyle \ theta> 0$ es un parámetro fijo. Considere la variable aleatoria 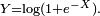$\ Scriptstyle Y = \ mathrm {log} (1 + e ^ {- X}).$ Luego,

$F_ {y} (y) = P (Y \ leq y) = P (\ mathrm {log} (1 + e ^ {- X}) \ leq y) = P (X> - \ mathrm {log} (e ^ {y} -. 1)) \,$

La última expresión se puede calcular en términos de la distribución acumulada de 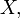$X,$ así

$F_ {Y} (y) = 1 - F_ {X} (- \ mathrm {log} (e ^ {y} - 1)) \,$

$= 1 - \ frac {1} {(1 + e ^ {\ mathrm {log} (e ^ {y} - 1)}) ^ {\ theta}}$

$= 1 - \ frac {1} {(1 + e ^ {y} - 1) ^ {\ theta}}$

$= 1 - e ^ {- y \ theta} \,.$

Equivalencia de las variables aleatorias

Hay varios sentidos diferentes en los que las variables aleatorias pueden ser considerados como equivalentes. Dos variables aleatorias pueden ser iguales, iguales casi con seguridad, la igualdad en la media, o igual en la distribución.

En orden creciente de la fuerza, la definición precisa de estas nociones de equivalencia es la siguiente.

La igualdad en la distribución

Dos variables aleatorias X e Y son iguales en distribución si tienen las mismas funciones de distribución:

$\ Operatorname {P} (X \ le x) = \ operatorname {P} (Y \ le x) \ quad \ hbox {for all} \ quad x.$

Dos variables aleatorias que tienen igual funciones generadoras momento tienen la misma distribución. Esto proporciona, por ejemplo, un método útil para comprobar la igualdad de determinadas funciones de iidrv de.

Para ser igual en la distribución, variables aleatorias no tienen que ser definidas en el mismo espacio de probabilidad. La noción de equivalencia en la distribución está asociada a la siguiente noción de distancia entre distribuciones de probabilidad,

$d (X, Y) = \ sup_x | \ operatorname {P} (X \ le x) - \ operatorname {P} (Y \ le x) |,$

que es la base de la Prueba de Kolmogorov-Smirnov.

La igualdad en la media

Dos variables aleatorias X e Y son iguales en p-ésima significa si el p ésimo momento de | X - Y | es cero, es decir,

$\ Operatorname {E} (| X-Y | ^ p) = 0.$

La igualdad en el orden p media implica igualdad en q ª media para todo q <p. Como en el caso anterior, hay una distancia relacionada entre las variables aleatorias, a saber,

$D_P (X, Y) = \ operatorname {E} (| X-Y | ^ p).$

Casi seguro de igualdad

Dos variables aleatorias X e Y son iguales casi seguro que si, y sólo si, la probabilidad de que son diferentes es cero:

$\ Operatorname {P} (X \ neq Y) = 0.$

Para todos los efectos prácticos de la teoría de la probabilidad, esta noción de equivalencia es tan fuerte como la igualdad real. Se asocia a la distancia de seguimiento:

$d_ \ infty (X, Y) = \ sup_ \ omega | X (\ omega) -Y (\ omega) |,$

donde 'sup' en este caso representa la supremum esencial en el sentido de medir teoría.

Igualdad

Finalmente, las dos variables aleatorias X e Y son iguales si son iguales como funciones en su espacio de probabilidad, es decir,

$X (\ omega) = S (\ omega) \ qquad \ hbox {for all} \ quad \ omega$

Convergencia

Gran parte de la estadística matemática consiste en probar los resultados de convergencia para ciertas secuencias de variables aleatorias; véase por ejemplo la ley de los grandes números y el teorema del límite central.

Hay varios sentidos en los que una secuencia (X _n) de variables aleatorias pueden converger a una variable aleatoria X. Esto se explica en el artículo sobre convergencia de las variables aleatorias.

Literatura

Kallenberg, O., Medidas azar, cuarta edición. Academic Press, Nueva York, Londres; Akademie-Verlag, Berlin (1986). MR0854102 ISBN 0123949602
Papoulis, Athanasios 1965 Probabilidad, Variables aleatorias y procesos estocásticos. McGraw-Hill Kogakusha, Tokio, novena edición, ISBN 0-07-119981-0.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Random_variable&oldid=195646641 "