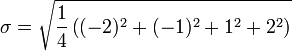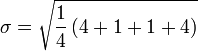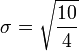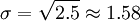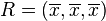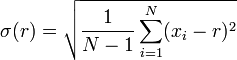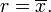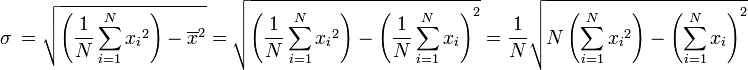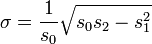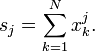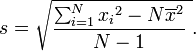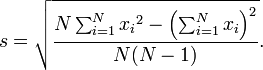Desviacion estandar
Antecedentes de las escuelas de Wikipedia
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Ver http://www.soschildren.org/sponsor-a-child para averiguar sobre el apadrinamiento de niños.
En probabilidad y estadísticas , la desviación estándar de una distribución de probabilidad , variable aleatoria , o población o multiset de los valores es una medida de la difusión de sus valores. La desviación estándar se denota generalmente con la letra σ (minúsculas sigma). Se define como la raíz cuadrada de la varianza .
Para entender la desviación estándar, tenga en cuenta que la varianza es la media de las diferencias al cuadrado entre los puntos de datos y la media. Varianza se tabula en unidades al cuadrado. La desviación estándar, siendo la raíz cuadrada de dicha cantidad, por lo tanto, mide la dispersión de los datos alrededor de la media, medida en las mismas unidades que los datos.
Dicho de manera más formal, la desviación estándar es la media cuadrática (RMS) desviación de los valores de su media aritmética .
Por ejemplo, en la población {4, 8}, la media es de 6 y las desviaciones de la media son {-2, 2}. Esas desviaciones cuadráticas son {4, 4} de la media de las cuales (la varianza) es 4. Por lo tanto, la desviación estándar es de 2. En este caso 100% de los valores en la población en una desviación estándar de la media.
La desviación estándar es la medida más común de dispersión estadística, que mide qué tan ampliamente difundir los valores en un empleando datos. Si muchos puntos de datos se encuentran cerca de la media, entonces la desviación estándar es pequeña; Si muchos puntos de datos están lejos de la media, a continuación, la desviación estándar es grande. Si todos los valores de datos son iguales, entonces la desviación estándar es cero.
Para población, la desviación estándar puede ser estimado por una desviación estándar modificado (s) de una muestra. Las fórmulas se dan a continuación.

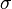 es una medida de la dispersión de los valores de la variable aleatoria lejos de su media
es una medida de la dispersión de los valores de la variable aleatoria lejos de su media 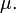
Definición y cálculo
Un ejemplo sencillo
Supongamos que deseamos encontrar la desviación estándar del conjunto de los números 4 y 8.
Paso 1: encontrar la media aritmética (o promedio) de 4 y 8,
Paso 2: encontrar la desviación de cada número de la media,
Paso 3: plaza cada una de las desviaciones (amplificando desviaciones mayores y haciendo valores negativos positivo),
Paso 4: suma los cuadrados obtenidos (como un primer paso para la obtención de un promedio),
Paso 5: dividir la suma por el número de valores, que aquí es 2 (dando un promedio),
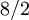 = 4.
= 4.
Paso 6: tomar la raíz cuadrada no negativa del cociente (conversión de unidades al cuadrado de nuevo a las unidades regulares),
Por lo tanto, la desviación estándar es de 2.
La desviación estándar de una variable aleatoria
La desviación estándar de una variable aleatoria X se define como:
donde E (X) es el valor esperado de X, y Var (X) es la varianza de x.
No todas las variables aleatorias tienen una desviación estándar, ya que estos No es necesario que existan valores esperados. Por ejemplo, la desviación estándar de una variable aleatoria que sigue una Distribución de Cauchy es indefinido debido a que su E (X) es indefinido.
Si la variable aleatoria X toma los valores 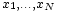 (Que son números reales ) con igual probabilidad, a continuación, su desviación estándar se puede calcular como sigue. En primer lugar, la media de X,
(Que son números reales ) con igual probabilidad, a continuación, su desviación estándar se puede calcular como sigue. En primer lugar, la media de X, 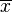 , Se define como una suma:
, Se define como una suma:
donde N es el número de muestras tomadas. A continuación, la desviación estándar se simplifica a
En otras palabras, la desviación estándar de una discreta uniforme variable aleatoria X se puede calcular como sigue:
- Para cada valor
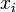 calcular la diferencia
calcular la diferencia 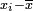 entre x i y el valor promedio
entre x i y el valor promedio  .
. - Calcular los cuadrados de estas diferencias.
- Encuentra la media de las diferencias al cuadrado. Esta cantidad es la varianza σ 2.
- Saca la raíz cuadrada de la varianza.
La expresión anterior también se puede reemplazar con
Igualdad de estas dos expresiones se puede demostrar un poco de álgebra:
La desviación estándar de una variable aleatoria continua
Distribuciones continuas suelen dar una fórmula para el cálculo de la desviación estándar como una función de los parámetros de la distribución. En, la desviación estándar general de una variable aleatoria continua X con la función de densidad de probabilidad p (x) es
Donde
Ejemplo
Le mostraremos cómo calcular la desviación estándar de una población. Nuestro ejemplo utilizará las edades de cuatro niños pequeños: {5, 6, 8, 9}.
Paso 1. Calcular la media aritmética , 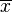 :
:
Tenemos N = 4 porque hay cuatro puntos de datos:
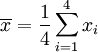 Sustituto N = 4
Sustituto N = 4
Paso 2. Calcular la desviación estándar, 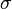 . (Desde los cuatro valores representan a toda la población, no utilizamos la fórmula para la desviación estándar estimada en este caso):
. (Desde los cuatro valores representan a toda la población, no utilizamos la fórmula para la desviación estándar estimada en este caso):
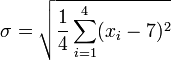 Sustituto
Sustituto 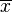 = 7 y N = 4
= 7 y N = 4
Así que la desviación estándar de las edades de los cuatro niños es la raíz cuadrada de 2,5, o aproximadamente 1,58.
Si este fuera establecido una muestra extraída de una población mayor de los niños, y la pregunta en cuestión era una estimación de la desviación estándar de la población, la convención reemplazaría el denominador N (o 4) en el paso 2 aquí con N-1 (o 3 ).
Interpretación y aplicación
Una desviación estándar grande indica que los puntos de datos están lejos de la media y una pequeña desviación estándar indica que se agrupan estrechamente alrededor de la media.
Por ejemplo, cada uno de los tres conjuntos de datos {0, 0, 14, 14}, {0, 6, 8, 14} y {6, 6, 8, 8} tiene una media de 7. Sus desviaciones estándar son 7, 5, y 1, respectivamente. El tercer conjunto tiene una desviación estándar mucho más pequeña que las otras dos porque sus valores están cerca de 7. En un sentido amplio, la desviación estándar nos dice qué tan lejos de los puntos: datos tienden a ser. Tendrá las mismas unidades que señala los datos mismos. Si, por ejemplo, el conjunto de datos {0, 6, 8, 14} representa las edades de cuatro hermanos en años, la desviación estándar es de 5 años.
Como otro ejemplo, el conjunto de datos {1000, 1006, 1008, 1014} puede representar las distancias recorridas por cuatro atletas, medido en metros. Tiene una media de 1.007 metros, y una desviación estándar de 5 metros.
La desviación estándar puede servir como una medida de la incertidumbre. En la ciencia física, por ejemplo, la desviación estándar informado de un grupo de repetidas mediciones debe dar la precisión de las mediciones. Al decidir si las mediciones están de acuerdo con una predicción teórica, la desviación estándar de las mediciones es de importancia crucial: si la media de las mediciones es demasiado lejos de la predicción (con la distancia medida en desviaciones estándar), entonces la teoría está probando probablemente necesita ser revisada. Esto tiene sentido ya que caen fuera del rango de valores que podrían razonablemente esperarse que ocurra si la predicción fuera correcta y la desviación estándar cuantificado adecuadamente. Ver intervalo de predicción.
Ejemplos de la vida real
El valor práctico de la comprensión de la desviación estándar de un conjunto de valores es en la apreciación de cuánta variación existe entre el "promedio" (media).
Tiempo
Como un simple ejemplo, considere las temperaturas medias de las ciudades. Mientras que dos ciudades pueden cada uno tener una temperatura promedio de 60 ° F, es útil para entender que el rango de las ciudades cercanas a la costa es menor que para las ciudades del interior, que aclara que, mientras que el promedio es similar, las posibilidades de variación es mayor en el interior que cerca de la costa.
Por lo tanto, un promedio de 60 se produce por una ciudad con máximas de 80 ° C y mínimas de 40 ° F, y también ocurre otra ciudad con máximas de 65 y mínimas de 55. La desviación estándar nos permite reconocer que la media de la ciudad con la mayor variación, y por lo tanto una mayor desviación estándar, no ofrecerá una predicción fiable de la temperatura como la ciudad con la menor variación y desviación estándar inferior.
Deportes
Otra forma de verlo es considerar los equipos deportivos. En cualquier conjunto de categorías, habrá equipos que clasifican altamente en algunas cosas y mal en otros. Es probable que, los equipos que llevan en la clasificación no se mostrará tal disparidad, pero será bastante bueno en la mayoría de categorías. Cuanto menor es la desviación estándar de sus calificaciones en cada categoría, más equilibrado y coherente que sean. Así, un equipo que es consistentemente mal en la mayoría de las categorías tendrá una baja desviación estándar. Un equipo que es muy buena en la mayoría de categorías también tendrá una baja desviación estándar. Un equipo con una desviación estándar de alta podría ser el tipo de equipo que anota muchos (buen ataque), pero también concede un montón (defensa débil), o, viceversa, que podrían tener un delito pobre pero compensa por ser difícil de marcar en -teams con una desviación estándar más alto será más impredecible.
Tratar de predecir cual los equipos, en un día cualquiera, ganará, pueden incluir la observación de las desviaciones estándar de los distintos equipo "stats" calificaciones, en el que las anomalías pueden igualar fortalezas frente a las debilidades para intentar entender qué factores pueden prevalecer como los indicadores más fuertes de los resultados eventuales de puntuación.
En las carreras, un conductor se mide el tiempo en las vueltas sucesivas. Un conductor con una baja desviación estándar de los tiempos de vuelta es más consistente que un conductor con una desviación estándar superior. Esta información se puede utilizar para ayudar a entender donde se podrían encontrar oportunidades para reducir los tiempos de vuelta.
Finanzas
En las finanzas, la desviación estándar es una representación de los riesgos asociados a un determinado valor (acciones, bonos, bienes, etc.), o el riesgo de una cartera de valores. El riesgo es un factor importante para determinar la forma de gestionar de manera eficiente una cartera de inversiones, ya que determina la variación en los rendimientos de los activos y / o cartera y da a los inversionistas una base matemática para las decisiones de inversión. El concepto general de riesgo es que a medida que aumenta, el rendimiento esperado de los activos se incrementará como consecuencia de la prima de riesgo ganado - en otras palabras, los inversores deben esperar un mayor retorno de la inversión cuando dicha inversión lleva a un mayor nivel de riesgo .
Por ejemplo, usted tiene una opción entre dos poblaciones: Stock A devuelve históricamente 5% con una desviación estándar de 10%, mientras que la acción B devuelve el 6% y lleva a una desviación estándar de 20%. Sobre la base de la rentabilidad y riesgo, un inversionista puede decidir que la acción A es la mejor opción, ya punto porcentual adicional de Stock B de retorno genera (un 20% adicional en términos de dólares) no vale el doble del grado de riesgo asociado con la acción A . Stock B es probable que caiga por debajo de la inversión inicial más a menudo que la acción A en las mismas circunstancias, y devolverá sólo un punto porcentual más en promedio. En este ejemplo, de la A tiene el potencial de ganar un 10% más que el rendimiento esperado, pero tiene la misma probabilidad de ganar un 10% menos que el retorno esperado.
El cálculo de la rentabilidad promedio (o media aritmética) de un valor en un número determinado de períodos generará un retorno esperado sobre el activo. Para cada período, restar el rendimiento que se espera de los resultados de retorno reales en la varianza. Cuadrar la varianza en cada período para conocer el efecto del resultado en el riesgo global del activo. Cuanto mayor sea la varianza en un período, el mayor riesgo de la seguridad lleva. Tomando el promedio de las varianzas cuadrado resulta en la medición de las unidades globales de riesgo asociados con el activo. Encontrar la raíz cuadrada de esta variación dará lugar a la desviación estándar de la herramienta de inversión en cuestión. Use esta medida, junto con el rendimiento medio de la seguridad, como base para la comparación de valores.
Interpretación geométrica
Para obtener algunas ideas geométricas, empezaremos con una población de tres valores, x 1, x 2, x 3. Esto define un punto P = (x 1, x 2, x 3) en R 3. Considere la línea L = {(r, r, r): r en R}. Esta es la "diagonal principal" pasar por el origen. Si nuestros tres valores dados eran todos iguales, entonces la desviación estándar sería cero y P radicaría en L. Así que no es descabellado suponer que la desviación estándar está relacionada con la distancia de P a L. Y eso es realmente el caso. Mover ortogonal de P a la línea L, uno golpea el punto:
cuyas coordenadas son la media de los valores que empezamos con. Un poco de álgebra muestra que la distancia entre P y R (que es la misma que la distancia entre P y la línea L) viene dada por σ√ 3. Una fórmula análoga (con 3 sustituido por N) también es válida para una población de N valores; entonces tenemos que trabajar en R N.
Reglas para datos distribuidos normalmente

En la práctica, a menudo se asume que los datos son de una aproximadamente una distribución normal de la población. Esta frecuencia se justifica por el clásico teorema del límite central, que dice que las sumas de muchas variables aleatorias independientes, idénticamente distribuidas tienden a la distribución normal como límite. Si esta suposición se justifica, a continuación, alrededor del 68% de los valores están dentro de 1 desviación estándar de la media, aproximadamente el 95% de los valores están dentro de dos desviaciones estándar y aproximadamente 99,7% se encuentran dentro de 3 desviaciones estándar. Esto se conoce como la 68-95-99.7 regla o la regla empírica.
La los intervalos de confianza son los siguientes:
| σ | 68.26894921371% |
| 2σ | 95.44997361036% |
| 3σ | 99.73002039367% |
| 4σ | 99.99366575163% |
| 5σ | 99.99994266969% |
| 6σ | 99.99999980268% |
| 7σ | 99.99999999974% |
Para distribuciones normales, los dos puntos de la curva que son una desviación estándar de la media son también la puntos de inflexión.
La desigualdad de Chebyshev
La desigualdad de Chebyshev demuestra que en cualquier conjunto de datos, casi la totalidad de los valores será más cerca del valor medio, donde el significado de "cerca" está especificado por la desviación estándar. La desigualdad de Chebyshev implica que para (casi) todas las distribuciones aleatorias, no sólo los normales, tenemos los siguientes límites más débiles:
- Al menos el 50% de los valores se encuentran dentro de √2 desviaciones estándar de la media.
- Al menos el 75% de los valores se encuentran dentro de 2 desviaciones estándar de la media.
- Al menos el 89% de los valores están dentro de 3 desviaciones estándar de la media.
- Al menos el 94% de los valores están dentro de los 4 desviaciones estándar de la media.
- Al menos el 96% de los valores están dentro de los 5 desviaciones estándar de la media.
- Al menos el 97% de los valores están dentro de los 6 desviaciones estándar de la media.
- Al menos el 98% de los valores están dentro de los 7 desviaciones estándar de la media.
Y, en general:
- Por lo menos (1 - 1 / k 2) x 100% de los valores se encuentran dentro de k desviaciones estándar de la media.
Relación entre la desviación estándar y la media
La media y la desviación estándar de un conjunto de datos se presentan por lo general juntos. En cierto sentido, la desviación estándar es una medida "natural" de dispersión estadística si el centro de los datos se mide respecto a la media. Esto es debido a la desviación estándar de la media es menor que desde cualquier otro punto. La declaración precisa es la siguiente: supongamos que x 1, ..., x n son números reales y definir la función:
Uso de cálculo , o simplemente por completando el cuadrado, es posible mostrar que σ (r) tiene un mínimo único en la media:
(Esto también se puede hacer con el álgebra bastante simple solo, ya σ 2 (r) se equipara a un polinomio de segundo grado).
La coeficiente de variación de una muestra es la relación de la desviación estándar de la media. Es un número adimensional que puede ser utilizado para comparar la cantidad de variación entre poblaciones con diferentes medios.
Métodos de cálculo rápidos
Un poco más rápido (significativamente para el funcionamiento de desviación estándar) forma de calcular la desviación estándar de la población está dada por la siguiente fórmula (aunque consideraciones deben hacerse para error de redondeo, desbordamiento aritmético, y condiciones underflow aritméticas):
o
donde las cantidades de energía s 0, S 1, S 2 se definen por
Del mismo modo para la desviación estándar de la muestra:
O se ejecute sumas:
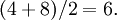
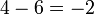
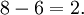
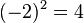
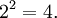
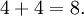
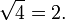
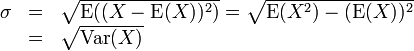
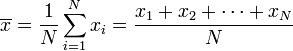
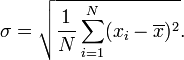
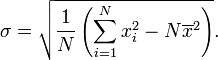
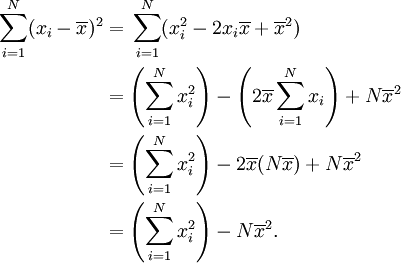
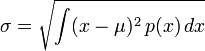
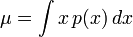
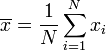

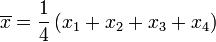
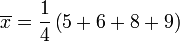
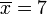
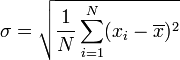
![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(x_1 - 7) ^ 2 + (x_2 - 7) ^ 2 + (x_3 - 7) ^ 2 + (x_4 - 7) ^ 2 \ right ]}](../../images/135/13580.png)
![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(5-7) ^ 2 + (6-7) ^ 2 + (8-7) ^ 2 + (9-7) ^ 2 \ right ]}](../../images/135/13581.png)