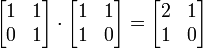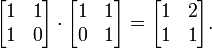Anillo conmutativo

Temas relacionados: Matemáticas

Antecedentes de las escuelas de Wikipedia

Esta selección Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Está disponible como una descarga intranet. El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.

En la teoría de anillos, una rama del álgebra abstracta , un anillo conmutativo es un anillo en el que la operación de multiplicación obedece la ley conmutativa . Esto significa que si a y b son los elementos del anillo, a continuación, a × b = b × a.

El estudio de los anillos conmutativos se llama álgebra conmutativa.

Ejemplos

El ejemplo más importante es el anillo de los enteros con las dos operaciones de adición y multiplicación. Multiplicación ordinaria de enteros es conmutativa. Este anillo está generalmente denotado Z en la literatura para significar la palabra alemana Zahlen (números).
Los racionales , reales y complejos números forman anillos conmutativos; De hecho, son incluso campos.
Más generalmente, cada campo es un anillo conmutativo, por lo que la clase de campos es una subclase de la clase de anillos conmutativos.
Un ejemplo simple de un anillo no conmutativo es la conjunto de todos los de 2 por 2 matrices cuyas entradas son números reales. Por ejemplo, la multiplicación de la matriz

$\ Begin {bmatrix} 1 & 1 \\ 0 & 1 \\ \ end {bmatrix} \ cdot \ begin {bmatrix} 1 & 1 \\ 1 & 0 \\ \ end {bmatrix} = \ begin {bmatrix} 2 & 1 \\ 1 & 0 \\ \ end {bmatrix}$

no es igual a la multiplicación se realiza en el orden inverso:

$\ Begin {bmatrix} 1 & 1 \\ 1 & 0 \\ \ end {bmatrix} \ cdot \ begin {bmatrix} 1 & 1 \\ 0 & 1 \\ \ end {bmatrix} = \ begin {bmatrix} 1 & 2 \\ 1 & 1 \\ \ end {bmatrix}.$

Si n es un entero positivo, entonces el conjunto Z de _n enteros módulo n forma un anillo conmutativo con n elementos (véase la aritmética modular ).
Si R es un anillo conmutativo dado, entonces el conjunto de todos los polinomios en la variable X cuyos coeficientes son en I forma un nuevo anillo conmutativo, denotado R [X].
Del mismo modo, el conjunto de series formales R [[X _1, ..., X _n]] sobre un anillo conmutativo R es un anillo conmutativo. Si R es un campo, el anillo de series de potencias formales es un tipo especial de anillo conmutativo, llamado completo anillo local.
El conjunto de todos los números racionales ordinarios cuyo denominador es formas extrañas un anillo conmutativo, de hecho, un anillo local. Este anillo contiene el anillo de los enteros correctamente, y es en sí mismo un subconjunto propio del campo racional.
Si p es cualquier número primo , el conjunto de p enteros -adic forma un anillo conmutativo.
Un conjunto de matrices que puede ser diagonalizarse con el mismo transformación de semejanza forma un anillo conmutativo. Un ejemplo es el conjunto de matrices de diferencias divididas con respecto a un conjunto fijo de nodos.

La construcción de anillos conmutativos

Dado un anillo conmutativo, se puede utilizar para construir nuevos anillos, como se describe a continuación.

Anillo Factor: Dado un anillo conmutativo R y un ideales I de R, la anillo factor de R / I es el conjunto de clases laterales de I junto con las operaciones de (a + I) + (B + i) = (a + b) + I y (a + I) (b + I) = ab + I .
Localización: Si S es un subconjunto multiplicativo de un anillo conmutativo R entonces podemos definir el localización de R en S, o un anillo de fracciones con denominadores en S, por lo general denota S ^-1. El ejemplo penúltima arriba es la localización del anillo de enteros en el subconjunto multiplicativo de enteros impares. El campo de los racionales es la localización del anillo conmutativo de enteros en el conjunto multiplicativo de enteros distintos de cero.
Finalización: Si I es un ideal en un anillo conmutativo R, los poderes de I forman barrios topológicas de 0 que permiten R para ser visto como un anillo topológico. Esta topología se llama la topología -adic I. R puede entonces ser completada con respecto a esta topología. Formalmente, la finalización -adic I es la límite inverso de los anillos R / I ^n. Por ejemplo, si k es un campo, K [[X]], la anillo de las series formales en una variable sobre k, es la finalización -adic I de k [X] donde I es el ideal director generada por X. Análogamente, el anillo de los enteros p -adic es la finalización -adic I de Z donde I es el ideal director generada por p.
Si R es un anillo conmutativo dado, el conjunto de todos los polinomios R [X _1, ..., X _n] más de R forma un nuevo anillo conmutativo, llamado anillo de polinomios en n variables más R.
Si R es un anillo conmutativo dado, entonces el conjunto de todos series formales R [[X _1, ..., X _n]] sobre un anillo conmutativo R es un anillo conmutativo, llamado el anillo de series de potencias en n variables más R.

Propiedades

Todos subanillos y anillos cociente de anillos conmutativos son también conmutativa.
Si f: R → S es una inyectiva homomorfismo de anillos (es decir, una monomorfismo) entre los anillos R y S, y si S es conmutativo, entonces R debe ser también conmutativa, ya que f (a · b) = f (a) · f (b) = f (b) · f (a) = f (b · a).
Del mismo modo, si f: R → S es una homomorfismo de anillos entre los anillos R y S, y si R es conmutativo, el subanillo f (R) de S también es conmutativo; En particular, si f es sobreyectiva (y por lo tanto una epimorfismo), S debe ser conmutativo.
Cada finito anillo de división es conmutativa ( El teorema de Wedderburn). N. Jacobson ha demostrado que la siguiente condición es suficiente: si R es un anillo de tal manera que para cada elemento x de R existe allí un número entero n> 1 tal que x = x ^n, entonces R es conmutativo. Condiciones mucho más generales que garantizan la conmutatividad de un anillo fueron posteriormente descubierto por EN Herstein y otros.

Discusión General

La estructura interna de un anillo conmutativo se determina considerando sus ideales. Todos los ideales de un anillo conmutativo son dos caras, lo que simplifica considerablemente la situación.

La estructura exterior de un anillo conmutativo se determina considerando el álgebra lineal sobre ese anillo, es decir, mediante la investigación de la teoría de su módulos. Este tema es mucho más difícil cuando el anillo conmutativo no es un campo y por lo general se llama álgebra homológica. El conjunto de ideales dentro de un anillo conmutativo R se puede caracterizar exactamente como el conjunto de -modules R que son submódulos de R.

Un elemento A de un anillo conmutativo (con identidad) se llama una unidad si posee un inverso multiplicativo, es decir, si existe otro elemento b del anillo (con b no necesariamente distinta de a) de manera que ab = 1. Cada elemento no nulo de un campo es una unidad. Cada elemento de un anillo local conmutativa no contenida en el ideal máximo es una unidad.

Un elemento distinto de cero a de un anillo conmutativo se dice que es una divisor de cero si existe un elemento no nulo b del anillo tal que ab = 0. Un anillo conmutativo con identidad que no posee divisores cero se denomina dominio de integridad, ya que se parece mucho a los números enteros en algunos aspectos.

Algunos tipos específicos de anillos conmutativos se dan con la siguiente cadena de inclusiones:

anillos conmutativos ⊃ dominios integrales ⊃ dominios de factorización única ⊃ principales dominios ideales ⊃ Dominios euclídeos ⊃ campos

Otra cadena posible (que es más geométrica) es la siguiente cadena de inclusiones:

Anillos Cohen-Macaulay ⊃ Anillos Gorenstein ⊃ Anillos regulares ⊃ Anillos locales regulares

Recuperado de " http://en.wikipedia.org/w/index.php?title=Commutative_ring&oldid=197903565 "