Homeomorfismo

Una deformación continua entre una taza de café y una dona ilustrando que son homeomorfo. Pero allí no tiene que ser una deformación continua por dos espacios sean homeomorfo.

En la matemática campo de la topología , un homeomorfismo o isomorfismo topológico (de los griegos palabras homoios = similar y μορφή (morphe) = = forma formulario (deformación latina de morphe)) es un especial isomorfismo entre espacios topológicos que respeta propiedades topológicas. Dos espacios con un homeomorfismo entre ellos se llaman homeomorfo. Desde un punto de vista topológico que son la misma.

En términos generales, un espacio topológico es un geométrico objeto, y el homeomorfismo es el estiramiento de un continuo y flexión del objeto en una nueva forma. Por lo tanto, un cuadrado y un círculo son homeomorfo a la otra, sino una esfera y una rosquilla no lo son. Una broma a menudo repetida es que topologists no pueden decir la taza de café de los que están bebiendo de la rosquilla que están comiendo, ya que un donut suficientemente flexible podría ser reconfigurado a la forma de una taza de café mediante la creación de un hoyuelo y progresivamente ampliarlo , mientras que la reducción de el agujero en un mango.

Intuitivamente, unos mapas homeomorfismo puntos en el primer objeto que se "cierran juntos" para puntos en el segundo objeto que están muy juntos, y los puntos en el primer objeto que no están muy juntos a puntos en el segundo objeto que no están muy juntas. La topología es el estudio de las propiedades de los objetos que no cambian cuando se aplican homeomorfismos.

Definición

Una función f entre dos espacios topológicos X e Y se llama un homeomorfismo si tiene las siguientes propiedades:

• f es una biyección ( 1-1 y a),
• f es continua,
• la función inversa f ^-1 es continua (f es una función abierta).

Si existe una función de este tipo, decimos X e Y son homeomorfo. Un auto-homeomorfismo es un homeomorfismo de un espacio topológico y ella misma. Los homeomorfismos forman una relación de equivalencia en el clase de todos los espacios topológicos. La resultante clases de equivalencia se llaman clases homeomorfismo.

Ejemplos

La nudo de trébol es homeomorfo a un toro . Si bien esto puede parecer ilógico, en cuatro dimensiones que pueden fácilmente ser deformadas continuamente.

• La unidad de 2- disco D ² y el cuadrado de la unidad en ^R2 son homeomorfo.

• El abierto intervalo (-1, 1) es homeomorfo al números reales R.

• La espacio del producto S ¹ × S ¹ y el dos dimensionales toro son homeomorfo.

• Cada isomorfismo uniforme y isomorfismo isométrico es un homeomorfismo.

• Cualquier 2-esfera con un solo punto eliminado es homeomorfo al conjunto de todos los puntos en R ² (un 2-dimensional de avión ).

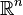• y 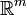no son para homeomorfo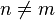

Propiedades

• Dos espacios homeomórficos comparten la misma propiedades topológicas. Por ejemplo, si uno de ellos es compacto , entonces el otro es así; si uno de ellos es conectado, entonces el otro es así; si uno de ellos es Hausdorff, entonces el otro es así; su grupos de homología coincidirán. Recuerde que esto no se extiende a las propiedades definidas a través de un métrica; hay espacios métricos que son homeomorfo a pesar de que uno de ellos es completar y el otro no.

• Un homeomorfismo es simultáneamente un función abierta y un mapeo cerrado, es decir que los mapas conjuntos abiertos para abrir conjuntos y conjuntos cerrados a conjuntos cerrados.

• Cada auto en homeomorfismo 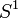se puede extender a un auto-homeomorfismo de todo el disco 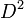( Truco de Alejandro).

Debate oficioso

El criterio intuitiva de estiramiento, doblado, corte y pegado de nuevo juntos necesita una cierta cantidad de la práctica de aplicar correctamente - puede no ser obvio a partir de la descripción anterior que deformar una segmento de línea a un punto es inadmisible, por ejemplo. Por tanto, es importante darse cuenta de que es la definición formal dada anteriormente que cuenta.

Esta caracterización de un homeomorfismo a menudo conduce a la confusión con el concepto de homotopy , que en realidad es definida como una deformación continua, pero a partir de una función a otra, en lugar de un espacio a otro. En el caso de un homeomorfismo, previendo una deformación continua es una herramienta mental para hacer el seguimiento de lo que apunta en el espacio X se corresponden con lo que apunta en Y - uno solo los sigue como X deforma. En el caso de homotopy, la deformación continua de un mapa a otro es de la esencia, y también es menos restrictiva, ya que ninguno de los mapas involucradas necesitan ser uno-a-uno o sobre. Homotopía conduce a una relación de espacios: la equivalencia de homotopía .

Hay un nombre para el tipo de deformación que participan en la visualización de un homeomorfismo. Es (excepto cuando el corte y regluing son obligatorios) una isotopía entre el mapa de identidad en X y el homeomorfismo de X a Y.