
Espacio compacto
Antecedentes
SOS cree que la educación da una mejor oportunidad en la vida para los niños en el mundo en desarrollo también. ¿Quieres saber sobre el patrocinio? Ver www.sponsorachild.org.uk
En matemáticas , un subconjunto del espacio euclidiano R n se llama compacto si es cerrado y delimitada. Por ejemplo, en R, la cerrada intervalo de la unidad [0, 1] es compacto, pero el conjunto de números enteros Z no es (no está limitada) y tampoco lo es el medio abierta intervalo [0, 1) (no es cerrado).
Un enfoque más moderno es llamar a un topológico compacto espacio si cada uno de sus tapas abiertas tiene una subcover finito. La Heine-Borel teorema muestra que esta definición es equivalente a "cerrada y delimitada" para subconjuntos de espacio euclidiano.
Nota: Algunos autores como Bourbaki utiliza el término "cuasi-compacto" en su lugar, y reservar el término "pacto" para espacios topológicos que son Hausdorff y "cuasi-compacto". Un solo conjunto compacto se conoce como un compactum veces; siguiendo el América segunda declinación (neutro), la forma plural correspondiente es compacta.
Historia y motivación
El término fue introducido por compacto Fréchet en 1906 .
Desde hace tiempo se ha reconocido que una propiedad como la compacidad es necesario probar muchos teoremas útiles. Solía ser que "compacta" significaba "secuencialmente compacto" (cada secuencia tiene una subsecuencia convergente). Esto fue cuando principalmente Se estudiaron los espacios métricos. La definición "que cubre compacto" se ha vuelto más prominente, ya que nos permite considerar los espacios topológicos generales, y muchos de los viejos resultados sobre espacios métricos se puede generalizar a este ajuste. Esta generalización es particularmente útil en el estudio de espacios de funciones, muchas de las cuales no son espacios métricos.
Una de las principales razones para estudiar espacios compactos es porque son en algunos aspectos muy similares a conjuntos finitos: hay muchos resultados que son fáciles de demostrar para conjuntos finitos, cuyas pruebas trasladará con un cambio mínimo para espacios compactos. A menudo se dice que "la compacidad es la mejor cosa siguiente a la finitud". He aquí un ejemplo:
- Supongamos que X es una Espacio de Hausdorff, y tenemos un punto x en X y un subconjunto finito A de X no contiene x. Entonces podemos x y A separados por barrios: para cada una en una, permiten U (x) y V (a) sean barrios inconexos que contienen x y una, respectivamente. Entonces la intersección de toda la U (x) y la unión de toda la V (a) son los barrios solicitada de x y A.
Tenga en cuenta que si A es infinito, la prueba falla, porque la intersección de manera arbitraria muchos barrios de x podría no ser un entorno de x. La prueba puede ser "rescatado", sin embargo, si A es compacto: simplemente tomamos una subcover finito de la cubierta {V (a)} de A. De esta manera, vemos que en un espacio de Hausdorff, cualquier punto puede ser separado por las vecindades de cualquier conjunto compacto no lo contiene. De hecho, repitiendo el argumento muestra que dos conjuntos compactos disjuntos en un espacio de Hausdorff se pueden separar por barrios - en cuenta que esto es precisamente lo que obtenemos si reemplazamos "punto" (es decir, singleton conjunto) con "conjunto compacto" en el Hausdorff axioma de separación. Muchos de los argumentos y resultados que implican espacios compactos siguen un patrón.
Definiciones
La compacidad de subconjuntos de R n
Para cualquier subconjunto del espacio euclidiano R n, las siguientes cuatro condiciones son equivalentes:
- Cada cubierta abierta tiene una finita subcover. Esta es la definición más comúnmente utilizado.
- Cada secuencia en el conjunto tiene una subsecuencia convergente, el punto de que el límite pertenece al conjunto.
- Cada subconjunto infinito de la serie tiene un punto de acumulación en el conjunto.
- El conjunto es cerrado y delimitada. Esta es la condición que es más fácil de verificar, por ejemplo, un cerrado intervalo o cerrada n -rodamientos.
En otros espacios, estas condiciones pueden o pueden no ser equivalentes, dependiendo de las propiedades del espacio.
Tenga en cuenta que mientras que la compacidad es una propiedad del propio conjunto (con su topología), encierro es relativa a un espacio que está en; por encima de "cerrado" se utiliza en el sentido de cerrado en R n. Un conjunto que está cerrado en, por ejemplo Q n normalmente no está cerrado en R n, por lo tanto, no compacto.
La compacidad de espacios topológicos
La propiedad "subcover finito" del párrafo anterior es más abstracto que el "cerrado y acotado" uno, pero tiene la ventaja de que se puede administrar utilizando el topología del subespacio en un subconjunto de R n, eliminando la necesidad de utilizar una métrica o un espacio de ambiente. Por lo tanto, la compacidad es una propiedad topológica. En cierto sentido, el intervalo unitario cerrado [0,1] es intrínsecamente compacto, independientemente de cómo se integra en I o R n.
Un espacio topológico X se define como compacto si todos sus tapas abiertas tienen un subcover finito. Formalmente, esto significa que
- para cada colección arbitraria
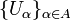 subconjuntos de abiertos de
subconjuntos de abiertos de 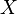 de tal manera que
de tal manera que 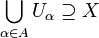 , Hay un subconjunto finito
, Hay un subconjunto finito 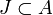 de tal manera que
de tal manera que 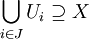 .
.
Una definición equivalente utilizado a menudo se da en términos de la propiedad intersección finita: si cualquier colección de conjuntos cerrados que satisfacen la propiedad intersección finita tiene intersección no vacía, entonces el espacio es compacto. Esta definición es dual a la habitual declarado en términos de conjuntos abiertos.
Algunos autores requieren que un espacio compacto ser también Hausdorff, y la versión no Hausdorff se llama entonces quasicompact.
Ejemplos de espacios compactos
- Cualquier espacio topológico finito, incluyendo el conjunto vacío, es compacto. Algo más en general, cualquier espacio con una topología finita (sólo un número finito de conjuntos abiertos) es compacto; esto incluye, en particular, la topología trivial.
- El cerrado intervalo de unidad
![[0, 1]](../../images/108/10846.png) es compacto. Así se desprende del Teorema de Heine-Borel; demostrando que el teorema es casi tan difícil como probar directamente que
es compacto. Así se desprende del Teorema de Heine-Borel; demostrando que el teorema es casi tan difícil como probar directamente que ![[0,1]](../../images/108/10846.png) es compacto. El intervalo abierto
es compacto. El intervalo abierto 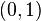 no es compacto: la cubierta abierta
no es compacto: la cubierta abierta 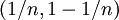 para
para 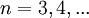 no tiene un subcover finito.
no tiene un subcover finito. - Para cada número natural n, el n - esfera es compacto. Una vez más desde el teorema de Heine-Borel, la bola unidad cerrada de cualquier dimensión finita espacio vectorial normado es compacto. Esto no es cierto para las dimensiones infinitas; de hecho, un espacio vectorial normado es de dimensión finita si y sólo si su bola unidad cerrada es compacto.
- La Conjunto de Cantor es compacto. Desde el p enteros -adic son homeomorfo al conjunto de Cantor, que también forman un conjunto compacto. Dado un conjunto finito que contiene los elementos p es compacto, esto demuestra que el contable producto de conjuntos finitos es compacto, y es por lo tanto un caso especial de El teorema de Tychonoff.
- Consideremos el conjunto
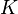 de todas las funciones
de todas las funciones ![f: \ mathbb {R} \ rightarrow [0,1]](../../images/108/10850.png) desde la línea número real al intervalo unidad cerrada, y definir una topología en
desde la línea número real al intervalo unidad cerrada, y definir una topología en 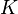 de manera que una secuencia
de manera que una secuencia 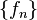 en
en 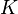 converge hacia
converge hacia 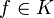 si y solo si
si y solo si 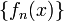 converge hacia
converge hacia 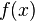 para todos
para todos 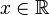 . Sólo hay una tal topología; se llama el topología de la convergencia puntual. Entonces
. Sólo hay una tal topología; se llama el topología de la convergencia puntual. Entonces 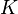 es un espacio topológico compacto, una vez más una consecuencia del teorema de Tychonoff.
es un espacio topológico compacto, una vez más una consecuencia del teorema de Tychonoff. - Consideremos el conjunto
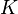 de todas las funciones
de todas las funciones ![f \ de colon [0,1] \ a [0,1]](../../images/108/10856.png) satisfacer la Condición de Lipschitz
satisfacer la Condición de Lipschitz 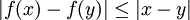 para todos
para todos ![x, y \ in [0,1]](../../images/108/10858.png) y considerar en
y considerar en 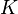 la métrica inducida por la distancia uniforme
la métrica inducida por la distancia uniforme ![d (f, g) = \ sup \ {| f (x) -g (x) | \ dos puntos x \ in [0,1] \}](../../images/108/10859.png) . Entonces por Ascoli-Arzelà teorema del espacio
. Entonces por Ascoli-Arzelà teorema del espacio 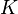 es compacto.
es compacto. - Cualquier espacio que lleva el topología cofinite es compacto.
- Cualquier espacio localmente compacto de Hausdorff se puede convertir en un espacio compacto añadiendo un solo punto a la misma, por medio de Alexandroff compactificación de un punto. La compactación de un punto de
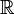 es homeomorfo al círculo
es homeomorfo al círculo 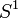 ; la compactación de un punto de
; la compactación de un punto de 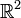 es homeomorfo a la esfera
es homeomorfo a la esfera 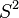 . Utilizando la compactación de un punto, también se puede construir fácilmente espacios compactos que no son Hausdorff, comenzando con un espacio no Hausdorff.
. Utilizando la compactación de un punto, también se puede construir fácilmente espacios compactos que no son Hausdorff, comenzando con un espacio no Hausdorff. - La espectro de cualquier continuo operador lineal en una Espacio de Hilbert es un subconjunto compacto del número complejo C. Si el espacio de Hilbert es de dimensión infinita, entonces cualquier subconjunto compacto de C surge de esta manera, como el espectro de algún operador lineal continua en el espacio de Hilbert.
- La espectro de cualquier anillo conmutativo o Álgebra de Boole es compacto.
- La Hilbert cubo es compacto.
- La topología orden correcto o topología orden izquierda de una limitada conjunto totalmente ordenado es compacto. En particular, Espacio de Sierpinski es compacto.
- La espectro principal de cualquier anillo conmutativo con la Topología de Zariski es un espacio compacto, importante en geometría algebraica. Estos espectros primos son casi nunca Los espacios de Hausdorff.
Teoremas
Algunos teoremas relacionados con la compacidad (ver el Glosario de topología para las definiciones):
- La imagen continua de un espacio compacto es compacto.
- La teorema del valor extremo: una función real continua en un espacio compacto no vacío está acotado y alcanza su valor supremo.
- Un subconjunto cerrado de un espacio compacto es compacto.
- Un subconjunto compacto de una Espacio de Hausdorff es cerrado.
- Un subconjunto compacto no vacío de los números reales tiene un mayor elemento y un elemento menor.
- Un subconjunto de n-espacio euclidiano es compacto si y sólo si está cerrada y delimitada. ( Teorema de Heine-Borel)
- La espacio métrico (o espacio uniforme) es compacto si y sólo si es completa y totalmente acotado.
- La producto de cualquier colección de espacios compactos es compacto. ( Teorema de Tychonoff, que es equivalente a la axioma de elección)
- Un espacio compacto de Hausdorff es normal.
- Cada mapa continua a partir de un espacio compacto a un espacio de Hausdorff es cerrado y adecuada. De ello se sigue que cada continuo mapa biyectiva de un espacio compacto de un espacio de Hausdorff es un homeomorfismo .
- Un espacio métrico (o más generalmente cualquier primero-contable espacio uniforme) es compacto si y sólo si cada secuencia en el espacio tiene una subsecuencia convergente.
- Un espacio topológico es compacto si y sólo si cada neta en el espacio tiene una subred convergente.
- Un espacio topológico es compacto si y sólo si cada filtro en el espacio tiene un refinamiento convergente.
- Un espacio topológico es compacto si y sólo si cada ultrafiltro en el espacio es convergente.
- Un espacio topológico puede ser embebido en un espacio compacto de Hausdorff si y sólo si es una Espacio Tychonoff.
- Cada espacio topológico X es un densa subespacio de un espacio compacto que tenga como máximo un punto más que X. ( Alexandroff un punto compactificación)
- Si el espacio métrico X es compacto y se le da una cobertura abierta de X, entonces existe un número δ> 0 tal que cada subconjunto de X de diámetro <δ está contenido en algún miembro de la cubierta. ( Número de Lebesgue)
- Si un espacio topológico tiene una sub-base de manera que todas las portadas del espacio por miembros de la sub-base tiene un subcover finito, entonces el espacio es compacto. ( Teorema de sub-base de Alexander)
- Dos compactos los espacios de Hausdorff X 1 y X 2 son homeomorfa si y sólo si su anillos de continuas con valores reales funciones C (X 1) y C (X 2) son isomorfos. ( Gelfand-Naimark teorema)
Otras formas de compacidad
Hay un número de propiedades topológicas que son equivalentes a la compacidad en espacios métricos, pero son no equivalentes en espacios topológicos generales. Estos incluyen los siguientes.
- Secuencialmente compacto: Cada secuencia tiene una subsecuencia convergente.
- Numerable compacto: Cada cubierta abierta contable tiene un subcover finito. (O, equivalentemente, todo subconjunto infinito tiene un punto ω-acumulación.)
- Pseudocompact: Cada valor real- continua función en el espacio es limitado.
- Débilmente numerable compacto (o punto límite compacto): Cada subconjunto infinito tiene una punto de acumulación.
Si bien todas estas condiciones son equivalentes para espacios métricos, en general, tenemos las siguientes consecuencias:
- Espacios compactos son numerable compacto.
- Secuencialmente espacios compactos son numerable compacto.
- Numerable espacios compactos son pseudocompact y débilmente numerable compacto.
No todo el espacio numerable compacto es compacto; un ejemplo es dado por la primera ordinal incontable con la topología de orden. No todo el espacio compacto es secuencialmente compacto; un ejemplo es dado por 2 [0,1], con la topología producto.
Un espacio métrico se llama pre-compacto o totalmente limitada si cualquier secuencia tiene una subsecuencia de Cauchy; Esto se puede generalizar a espacios uniformes. Para espacios métricos completos esto es equivalente a la compacidad. Ver relativamente compacto para la versión topológica.
Otra idea relacionada que (por la mayoría de las definiciones) es estrictamente más débil que la compacidad es compacidad local.
