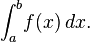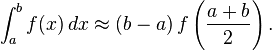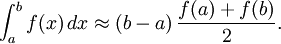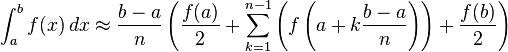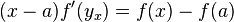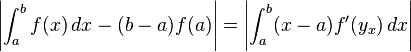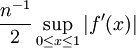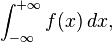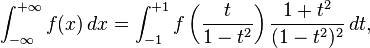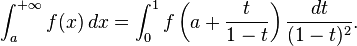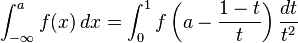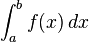Integraci??n num??rica

Temas relacionados: Matem??ticas

Antecedentes

Esta selecci??n Wikipedia est?? disponible sin conexi??n de SOS Children para su distribuci??n en el mundo en desarrollo. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/

Integraci??n num??rica consiste en encontrar aproximaciones num??ricas para el valor $S$

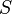
En an??lisis num??rico, la integraci??n num??rica constituye una amplia familia de algoritmos para el c??lculo del valor num??rico de un definido integral , y, por extensi??n, el t??rmino tambi??n se utiliza a veces para describir la soluci??n num??rica de ecuaciones diferenciales. Este art??culo se centra en el c??lculo de integrales definidas. El t??rmino cuadratura num??rica (a menudo abreviado como cuadratura) es m??s o menos un sin??nimo de integraci??n num??rica, especialmente en relaci??n a las integrales de una sola dimensi??n. Integraci??n num??rica sobre m??s de una dimensi??n se describe a veces como cubature, aunque el significado de cuadratura se entiende para una mayor integraci??n dimensional tambi??n.

El problema b??sico considerado por integraci??n num??rica es calcular una soluci??n aproximada a una integral definida:

$\ Int_a ^ b \! f (x) \, dx.$

Si $f (x)$ es una funci??n de buen comportamiento suave, integrada por un peque??o n??mero de dimensiones y los l??mites de integraci??n son limitadas, hay muchos m??todos de aproximaci??n de la integral con precisi??n arbitraria.

Razones para la integraci??n num??rica

Hay varias razones para llevar a cabo la integraci??n num??rica. El f integrando (x) puede ser conocido solamente en ciertos puntos, tal como se obtiene por muestreo . Algunos sistemas integrados y otras aplicaciones inform??ticas pueden necesitar integraci??n num??rica por esta raz??n.

Una f??rmula para el integrando puede ser conocida, pero puede ser dif??cil o imposible encontrar una antiderivada que es un funci??n elemental. Un ejemplo de un tal integrando es f (x) = exp (- x ^2), la primitiva de los cuales (el funci??n de error, los tiempos de una constante) no pueden ser escritos en forma elemental.

Puede ser posible encontrar una primitiva forma simb??lica, pero puede ser m??s f??cil de calcular una aproximaci??n num??rica que para calcular la antiderivada. Ese puede ser el caso si la primitiva se da como una serie infinita o producto, o si su evaluaci??n requiere una funci??n especial que no est?? disponible.

M??todos para integrales unidimensionales

M??todos de integraci??n num??rica generalmente pueden describirse como la combinaci??n de evaluaciones del integrando para obtener una aproximaci??n a la integral. El integrando se eval??a en un conjunto finito de puntos llamados puntos de integraci??n y una suma ponderada de estos valores se utiliza para aproximar la integral. Los puntos de integraci??n y pesos dependen del m??todo espec??fico utilizado y de la precisi??n requerida de la aproximaci??n.

Una parte importante del an??lisis de cualquier m??todo de integraci??n num??rica es estudiar el comportamiento del error de aproximaci??n como una funci??n del n??mero de evaluaciones del integrando. Un m??todo que produce un peque??o error para un peque??o n??mero de evaluaciones se considera generalmente superior. Reducir el n??mero de evaluaciones del integrando reduce el n??mero de operaciones aritm??ticas implicado, y por lo tanto reduce el total de error de redondeo. Adem??s, cada evaluaci??n lleva tiempo, y el integrando puede complicarse arbitrariamente.

Una especie "fuerza bruta" de la integraci??n num??rica se puede hacer, si el integrando es razonablemente buen comportamiento (es decir, a trozos continua y de variaci??n acotada), mediante la evaluaci??n del integrando con incrementos muy peque??os.

Reglas de cuadratura mediante funciones de interpolaci??n

Una gran clase de reglas de cuadratura se puede derivar mediante la construcci??n de interpolaci??n de funciones que son f??ciles de integrar. T??picamente, estas funciones de interpolaci??n son polinomios .

Ilustraci??n de la regla rect??ngulo.

El m??todo m??s simple de este tipo es dejar que la funci??n de interpolaci??n ser una funci??n constante (un polinomio de grado cero) que pasa por el punto ((a + b) / 2, f ((a + b) / 2)). Esto se conoce como la regla del punto medio o regla rect??ngulo.

$\ Int_a ^ bf (x) \, dx \ aprox (bis) \, f \ left (\ frac {a + b} {2} \ right).$

Ilustraci??n de la regla trapezoidal.

La funci??n de interpolaci??n puede ser una funci??n af??n (un polinomio de grado 1) que pasa por los puntos (a, f (a)) y (b, f (b)). Esto se llama el regla trapezoidal.

$\ Int_a ^ bf (x) \, dx \ aprox (bis) \, \ frac {f (a) + f (b)} {2}.$

Ilustraci??n de la regla de Simpson.

Para cualquiera de estas reglas, podemos hacer una aproximaci??n m??s precisa al romper el intervalo [a, b] en un n??mero n de subintervalos, calcular una aproximaci??n para cada subintervalo, entonces la suma de todos los resultados. Esto se llama una regla compuesta, regla extendida o regla iterativa. Por ejemplo, la regla del trapecio compuesta se puede plantear como

$\ Int_a ^ bf (x) \, dx \ aprox \ frac {ba} {n} \ left ({f (a) \ over 2} + \ sum_ {k = 1} ^ {n-1} \ left (f \ left (a + k \ frac {ba} {n} \ right) \ right) + {f (b) \ over 2} \ right)$

donde los subintervalos tienen la forma [k h, (k 1) h], con h = (b - a) / n y k = 0, 1, 2, ..., n -1.

La interpolaci??n con polinomios evaluados en puntos equidistantes en [a, b] se obtiene la F??rmulas de Newton-Cotes, de las cuales la regla rect??ngulo y la regla trapezoidal son ejemplos. La regla de Simpson, que se basa en un polinomio de orden 2, es tambi??n una f??rmula de Newton-Cotes.

Reglas de cuadratura con puntos equidistantes tienen la propiedad muy conveniente de anidaci??n. La regla correspondiente con cada intervalo subdividido incluye todos los puntos actuales, por lo que los valores del integrando se puede volver a utilizar.

Si permitimos que los intervalos entre puntos de interpolaci??n para variar, nos encontramos con otro grupo de f??rmulas de cuadratura, tales como la F??rmulas de cuadratura de Gauss. Una regla de cuadratura de Gauss es t??picamente m??s exacta que una regla de Newton-Cotes, que requiere el mismo n??mero de evaluaciones de la funci??n, si el integrando es suave (es decir, si es suficientemente diferenciable). Otros m??todos de cuadratura con intervalos variables incluyen Clenshaw-Curtis cuadratura (tambi??n llamada cuadratura Fej??r) m??todos, que hacen nido.

Reglas de cuadratura de Gauss no anidan, pero la relacionada F??rmulas de cuadratura de Gauss-Kronrod hacen.

Algoritmos adaptativos

Si f (x) no tiene muchos derivados en todos los puntos, o si los derivados se hacen grandes, entonces Cuadratura de Gauss es a menudo insuficiente. En este caso, un algoritmo similar al siguiente se obtienen mejores resultados:

 def calculate_definite_integral_of_f (f, initial_step_size): '' 'Este algoritmo calcula la integral definida de una funci??n de 0 a 1, de forma adaptativa, por la elecci??n de pasos m??s peque??os cerca de los puntos problem??ticos.  '' 'X = 0,0 h = initial_step_size acumulador = 0,0, mientras que x <1.0: si x + h> 1.0: h = 1,0 - x = quad_this_step si error_too_big_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_smaller (h ) else: acumulador + = quadrature_of_f_over_range (f, [x, x + h]) x + = h si error_too_small_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_larger (h) # Evite perder el tiempo en peque??os pasos. retorno acumulador

Algunos detalles del algoritmo requieren pensamiento cuidadoso. Para muchos casos, la estimaci??n del error de cuadratura en un intervalo para una funci??n f (x) no es obvia. Una soluci??n popular es el uso de dos reglas diferentes de cuadratura, y utilizar su diferencia como una estimaci??n del error de cuadratura. El otro problema es decidir qu?? "demasiado grande" o "muy peque??a" significan. Un criterio local para "demasiado grande" es que el error de cuadratura no debe ser mayor que t ?? h donde t, un n??mero real, es la tolerancia que queremos establecer para el error global. Por otra parte, si h es ya peque??o, puede que no valga la pena para que sea a??n m??s peque??o incluso si el error de cuadratura es aparentemente grande. Un criterio global es que la suma de errores en todos los intervalos debe ser inferior a t. Este tipo de an??lisis de errores por lo general se llama "a posteriori", ya que se calcula el error despu??s de haber calculado la aproximaci??n.

Heur??stica para cuadratura adaptativa son discutidos por Forsythe et al. (Secci??n 5.4).

M??todos de extrapolaci??n

La precisi??n de una regla de cuadratura del tipo Newton-Cotes es generalmente una funci??n del n??mero de puntos de evaluaci??n. El resultado es por lo general m??s precisa como el n??mero de puntos de evaluaci??n aumenta, o, equivalentemente, como la anchura de el tama??o de paso entre los puntos disminuye. Es natural preguntarse cu??l ser??a el resultado si el tama??o de paso se les permiti?? acercarse a cero. Esto puede responderse extrapolando el resultado de dos o m??s tama??os de paso no nulos, utilizando m??todos de aceleraci??n series como Extrapolaci??n de Richardson. La funci??n de extrapolaci??n puede ser un polinomio o funci??n racional. M??todos de extrapolaci??n se describen en m??s detalle por Stoer y Bulirsch (Secci??n 3.4) y se aplican en muchas de las rutinas en el Biblioteca QUADPACK.

Conservador (a priori) la estimaci??n de error

Sea f tiene una primera derivada acotada en [a, b]. La teorema del valor medio para f, donde x <b, da

$(X - a) f '(y_x) = f (x) - f (a) \,$

para algunos y _x en [a, x] en funci??n de x. Si integramos en x de A a B en ambos lados y tomar los valores absolutos, obtenemos

$\ Left | \ int_a ^ bf (x) \, dx - (b - a) f (a) \ right | = \ left | \ int_a ^ b (x - a) f '(y_x) \, dx \ right |$

Podemos aproximar a??n m??s la integral en el lado de la mano derecha por lo que el valor absoluto en el integrando, y reemplazando el t??rmino en f 'por un l??mite superior:

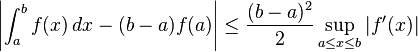$\ Left | \ int_a ^ bf (x) \, dx - (b - a) f (a) \ right | \ leq {(b - a) ^ 2 \ over 2} \ sup_ {a \ leq x \ leq b } \ left | f '(x) \ right |$ (**)

(Ver supremum) Por lo tanto, si nos aproximamos la integral ∫ _a ^b f (x) dx por la regla de cuadratura (b - a.) f (a) nuestro error no es mayor que el lado derecho de (**). Podemos convertir esto en un an??lisis de error para la suma de Riemann (*), dando un l??mite superior de

${N ^ {- 1} \ over 2} \ sup_ {0 \ leq x \ leq 1} \ left | f '(x) \ right |$

para el t??rmino de error de que la aproximaci??n particular. (Tenga en cuenta que este es precisamente el error se calcul?? para el ejemplo 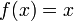$f (x) = x$ ). El uso m??s derivados, y por ajustar la cuadratura, podemos hacer un an??lisis de error similar utilizando una serie de Taylor (utilizando una suma parcial con plazo remanente) para f. Este an??lisis del error da una estricta l??mite superior en el error, si los derivados de f est??n disponibles.

Este m??todo de integraci??n se puede combinar con aritm??tica de intervalos para producir pruebas de ordenador y c??lculos verificados.

Integrales sobre intervalos infinitos

Intervalos de Infinite

Una manera de calcular una integral sobre intervalo infinito,

$\ Int _ {- \ infty} ^ {+ \ infty} f (x) \, dx,$

es para transformarla en una integral sobre un intervalo finito por uno cualquiera de varios cambios posibles de variables, por ejemplo:

$\ Int _ {- \ infty} ^ {+ \ infty} f (x) \, dx = \ int _ {- 1} ^ {+ 1} f \ left (\ frac {t} {1-t ^ 2} \ right ) \ frac {1 + t ^ 2} {(1-t ^ 2) ^ 2} \, dt,$

La integral sobre intervalo finito puede entonces ser evaluada por los m??todos de integraci??n ordinarios.

Intervalos de medio infinitas

Una integral durante un intervalo de media-infinito del mismo modo se puede transformar en una integral sobre un intervalo finito por uno cualquiera de los diversos cambios posibles de variables, por ejemplo:

$\ Int_a ^ {+ \ infty} f (x) \, dx = \ int_0 ^ 1 f \ left (a + \ frac {t} {1-t} \ right) \ frac {dt} {(1-t) ^ 2}.$

Del mismo modo,

$\ Int _ {- \ infty} ^ af (x) \, dx = \ int_0 ^ 1 f \ left (a - \ frac {1-t} {t} \ right) \ frac {dt} {t ^ 2}$

Integrales multidimensionales

Las reglas de cuadratura discutido hasta ahora todos han sido dise??ados para calcular integrales unidimensionales. Para calcular integrales en m??ltiples dimensiones, un enfoque consiste en la frase m??ltiplo entero como repetidas integrales unidimensionales apelando a El teorema de Fubini. Este enfoque requiere las evaluaciones de la funci??n a crecer de forma exponencial el n??mero de dimensiones aumenta. Dos m??todos son conocidos para superar esta llamada maldici??n de la dimensionalidad.

Monte Carlo

M??todos de Monte Carlo y m??todos cuasi-Monte Carlo son f??ciles de aplicar a integrales multidimensionales, y pueden producir una mayor precisi??n para el mismo n??mero de evaluaciones de la funci??n de integraciones repetidas utilizando m??todos unidimensionales.

Una gran clase de m??todos de Monte Carlo ??tiles son el llamado Algoritmos Monte Carlo cadena de Markov, que incluyen la Algoritmo de Metropolis-Hastings y Muestreo de Gibbs.

Redes dispersas

Rejillas Escasos fueron desarrollados originalmente por Smolyak para la cuadratura de las funciones de alta dimensi??n. El m??todo se basa siempre en una regla de cuadratura dimensional uno, pero lleva a cabo una combinaci??n m??s sofisticada de los resultados univariados.

Conexi??n con ecuaciones diferenciales

El problema de la evaluaci??n de la integral

$\ Int_a ^ b f (x) \, dx$

se puede reducir a una problema de valor inicial para una ecuaci??n diferencial ordinaria . Si la integral anterior se denota por I (b), entonces la funci??n I satisface

$I '(x) = f (x), \ quad I (a) = 0.$

Los m??todos desarrollados para ecuaciones diferenciales ordinarias, tales como M??todos de Runge-Kutta, se pueden aplicar al problema reexpresado y por lo tanto ser usados para evaluar la integral. Por ejemplo, el m??todo de Runge-Kutta de cuarto orden est??ndar aplicado a la ecuaci??n diferencial se obtiene la regla de Simpson desde arriba.

La ecuaci??n diferencial I '(x) = f (x) tiene una forma especial: la parte derecha contiene s??lo la variable dependiente (en este caso x) y no la variable independiente (aqu??). Esto simplifica la teor??a y algoritmos considerablemente. El problema de la evaluaci??n de las integrales de este modo se estudia mejor en su propio derecho.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Numerical_integration&oldid=544151167 "