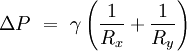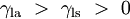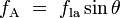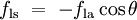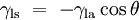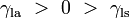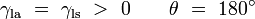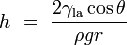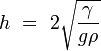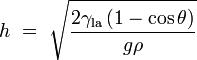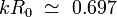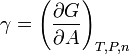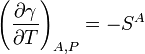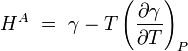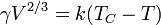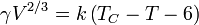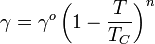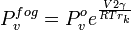Tensi??n superficial
Antecedentes
Esta selecci??n Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Est?? disponible como una descarga intranet. SOS Children ha cuidado de ni??os en ??frica durante cuarenta a??os. ??Puedes ayudar a su trabajo en ??frica ?
| Mec??nica de medios continuos |
|---|
 |
Leyes
|
Mec??nica de s??lidos
|
|
Reolog??a
|
La tensi??n superficial es una propiedad de la superficie de un l??quido que hace que se comporte como una hoja el??stica. Permite insectos , tales como la zancudo de agua (patinador estanque, Reino Unido ), para caminar sobre el agua . Se permite que los objetos peque??os, incluso los met??licos, tales como agujas, cuchillas de afeitar, o fragmentos de papel de aluminio, para flotar en la superficie del agua, y es la causa de acci??n capilar.
El comportamiento f??sico y qu??mico de los l??quidos no puede entenderse sin tener en cuenta la tensi??n superficial. Rige la forma que las peque??as masas de l??quido pueden asumir y el grado de contacto un l??quido puede hacer con otra sustancia.
La aplicaci??n de la f??sica newtoniana a las fuerzas que surgen debido a la tensi??n superficial predice con exactitud muchos comportamientos liquidez, que son tan comunes que la mayor??a de la gente los toma por sentado. La aplicaci??n de la termodin??mica a esas mismas fuerzas predice adem??s otros comportamientos l??quidos m??s sutiles.
Causa

La tensi??n superficial es causada por la atracci??n entre las mol??culas del l??quido por diversos fuerzas intermoleculares. En la mayor parte del l??quido cada mol??cula se tira igualmente en todas las direcciones por la vecina mol??culas de l??quido, que resulta en una fuerza neta de cero. En la superficie del l??quido, las mol??culas se tira hacia el interior por otras mol??culas m??s profundas dentro del l??quido y no se sienten atra??dos tan intensamente por las mol??culas en el medio vecino (ya sea vac??o, aire u otro l??quido). Por lo tanto todas las mol??culas en la superficie est??n sujetos a una fuerza hacia dentro de la atracci??n molecular que puede ser equilibrada s??lo por la resistencia del l??quido a la compresi??n. Este tir??n hacia el interior tiende a disminuir el ??rea de la superficie, y en este sentido una superficie l??quida se asemeja a una membrana el??stica estirada. Por lo tanto el l??quido en s?? aprieta juntos hasta que tenga la superficie localmente m??s bajo posible.
Otra forma de ver esto es que una mol??cula en contacto con un vecino est?? en un estado m??s bajo de energ??a que si no fuera en contacto con un vecino. Las mol??culas interiores todo tener tantos vecinos ya que posiblemente puede tener. Pero las mol??culas de frontera tienen menos vecinos que las mol??culas del interior y son, por tanto, en un estado superior de energ??a. Para el l??quido para reducir al m??nimo su estado de energ??a, se debe minimizar su n??mero de mol??culas de contorno y por lo tanto debe minimizar su ??rea de superficie.
Como resultado de la reducci??n al m??nimo de superficie, una superficie asumir?? la forma m??s suave que puede (prueba matem??tica de que las formas "suaves" minimizar superficie se basa en el uso de la Euler-Lagrange Ecuaci??n). Dado que cualquier curvatura en los resultados de forma superficial en ??rea metropolitana, tambi??n resultar?? una energ??a m??s alta. En consecuencia, la superficie se empuje hacia atr??s en contra de cualquier curvatura en la misma forma como una bola empujada hacia arriba se empuje hacia atr??s para minimizar su energ??a potencial gravitatoria.
Los efectos en la vida cotidiana
 |  El agua que cae de un grifo |
Algunos ejemplos de los efectos de la tensi??n superficial visto con agua ordinaria:
- Rebordear de agua de lluvia en la superficie de un autom??vil encerado. El agua se adhiere d??bilmente a la cera y fuertemente a s?? mismo, por lo que las agrupaciones de agua en gotas. Tensi??n superficial les da su forma casi esf??rica, porque una esfera tiene la superficie m??s peque??a posible en relaci??n al volumen.
- Formaci??n de gotas se produce cuando se estira una masa de l??quido. La animaci??n muestra el agua adherida a la masa grifo ganando hasta que se estira a un punto donde la tensi??n superficial ya no se unen al grifo puede. A continuaci??n, se separa y la tensi??n superficial forma la gota en una esfera. Si una corriente de agua estaban corriendo de la llave, la corriente se romper??a en gotas durante su ca??da. La gravedad se extiende la corriente, entonces la tensi??n superficial pellizca en esferas.
- Flotaci??n de los objetos m??s densos que el agua se produce cuando el objeto es no humectable y su peso es suficientemente peque??o para ser llevado por las fuerzas derivadas de la tensi??n superficial.
- La separaci??n de aceite y agua es causada por una tensi??n en la superficie entre l??quidos diferentes. Este tipo de tensi??n superficial se conoce con el nombre de "tensi??n interfacial", pero su f??sica son las mismas.
- Las l??grimas de vino es la formaci??n de gotas y riachuelos en el lado de un vidrio que contiene una bebida alcoh??lica. Su causa es una compleja interacci??n entre las diferentes tensiones superficiales de agua y etanol .
La tensi??n superficial es visible en otros fen??menos comunes, especialmente cuando ciertas sustancias, surfactantes, se utilizan para disminuirlo:
- Las burbujas de jab??n tienen muy grandes superficies con muy poco volumen. Burbujas en agua pura son inestables. El uso de tensioactivos, sin embargo, indroducir un efecto de estabilizaci??n de la burbuja (ver Efecto Marangoni). Observe que en realidad tensioactivos reducen la tensi??n superficial del agua por un factor de tres o m??s.
- Las emulsiones son un tipo de soluci??n en la que la tensi??n superficial juega un papel. Peque??os fragmentos de aceite en suspensi??n en el agua pura espont??neamente ensamblen en masas mucho m??s grandes. Pero la presencia de un agente tensioactivo proporciona una disminuci??n de la tensi??n superficial, que permite la estabilidad de las gotitas de aceite de minutos en la mayor parte de agua (o viceversa).
F??sica b??sica
Dos definiciones

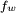 , Deprime la superficie, y se equilibra por las fuerzas de tensi??n superficial a cada lado,
, Deprime la superficie, y se equilibra por las fuerzas de tensi??n superficial a cada lado, 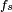 , Que son cada uno paralelo a la superficie del agua en los puntos donde entra en contacto con la aguja. Observe que los componentes horizontales de los dos
, Que son cada uno paralelo a la superficie del agua en los puntos donde entra en contacto con la aguja. Observe que los componentes horizontales de los dos 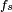 flechas apuntan en direcciones opuestas, por lo que se cancelan entre s??, pero los componentes verticales apuntan en la misma direcci??n y por lo tanto a??adir hasta equilibrar
flechas apuntan en direcciones opuestas, por lo que se cancelan entre s??, pero los componentes verticales apuntan en la misma direcci??n y por lo tanto a??adir hasta equilibrar 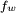 .
. La tensi??n superficial, representada por el s??mbolo σ, γ o T, se define como la fuerza a lo largo de una l??nea de unidad de longitud, donde la fuerza es paralela a la superficie, pero perpendicular a la l??nea. Una manera de representar esto es imaginar una pel??cula de jab??n plana limitada por un lado por un hilo tenso de longitud, L. El hilo ser?? tirado hacia el interior de la pel??cula por una fuerza igual a 2γL (el factor de 2 es porque la pel??cula de jab??n tiene dos lados por lo tanto, dos superficies). Por lo tanto, la tensi??n superficial se mide en fuerzas por unidad de longitud. Su Unidad SI es newton por metro pero el unidad cgs de dinas por cm es m??s com??nmente utilizado.
Una definici??n equivalente, que es ??til en la termodin??mica , es el trabajo realizado por unidad de ??rea. Como tal, con el fin de aumentar el ??rea de superficie de una masa de l??quido en una cantidad,? A, una cantidad de trabajo, γδA, se necesita. Este trabajo se almacena como energ??a potencial. En consecuencia la tensi??n superficial puede ser tambi??n midi?? en el sistema SI como julios por metro 2 y en el sistema CGS como ergios por 2 cm. Dado que los sistemas mec??nicos tratan de encontrar un estado de m??nima energ??a potencial, una gotita de l??quido libre asume naturalmente una forma esf??rica, que tiene la superficie m??nima para un volumen dado.
La equivalencia de medida de la energ??a por unidad de ??rea a la fuerza por unidad de longitud puede ser probada por an??lisis dimensional.
Striders del agua

Los espect??culos fotograf??a striders agua de pie sobre la superficie de un estanque. Es claramente visible que sus pies causan hendiduras en la superficie del agua. Y es intuitivamente evidente que la superficie con muescas tiene m??s superficie que una superficie plana. Si la tensi??n superficial tiende a minimizar la superficie, ??c??mo es que los zapateros est??n aumentando la superficie?
Recordemos que lo que la naturaleza realmente intenta minimizar es la energ??a potencial. Al aumentar el ??rea de superficie del agua, los striders de agua han aumentado la energ??a potencial de esa superficie. Pero tenga en cuenta tambi??n que el centro de masa de los zapateros 'es menor de lo que ser??a si ellos estaban de pie sobre una superficie plana. As?? que su energ??a potencial disminuye. De hecho cuando se combinan los dos efectos, la energ??a potencial neta se reduce al m??nimo. Si los zapateros deprimido la superficie m??s, el aumento de la energ??a superficial ser??a m??s que cancelar la energ??a disminuida de bajar el centro de la masa de los insectos. Si deprimido la superficie menos, su mayor centro de masa ser??a m??s que cancelar la reducci??n de la energ??a superficial.
La foto de los zapateros tambi??n ilustra la noci??n de la tensi??n superficial es como tener una pel??cula el??stica sobre la superficie del l??quido. En las depresiones de la superficie en sus pies es f??cil ver que la reacci??n de esa pel??cula el??stica imaginado se contrarrestando exactamente el peso de los insectos.
Curvatura de la superficie y la presi??n

Si no act??a ninguna fuerza normal a una superficie de tensado, la superficie debe permanecer plana. Pero si la presi??n en un lado de la superficie difiere de la presi??n en el otro lado, los resultados diferencia de presi??n en la zona de tiempos de la superficie en una fuerza normal. Para que las fuerzas de tensi??n superficial para cancelar la fuerza debida a la presi??n, la superficie debe ser curvada. El diagrama muestra c??mo curvatura de la superficie de un peque??o parche de la superficie conduce a un componente neto de fuerzas de tensi??n superficial que act??an normal al centro de la mancha. Cuando se equilibran todas las fuerzas, la ecuaci??n resultante es conocido como el Young-Laplace ecuaci??n:
donde:
- Δ P es la diferencia de presi??n.
- γ es la tensi??n superficial.
- R x y R y son radios de curvatura en cada uno de los ejes que son paralelos a la superficie.
Las soluciones a esta ecuaci??n determinan la forma de gotas de agua, charcos, meniscos, burbujas de jab??n, y todas las dem??s formas determinadas por la tensi??n superficial (por ejemplo, la forma de las impresiones que los pies de un Strider agua hacen en la superficie de un estanque).
La siguiente tabla muestra c??mo la presi??n interna de una gota de agua aumenta con la disminuci??n del radio. Para no gotas muy peque??as el efecto es sutil, pero la diferencia de presi??n se convierte en enorme cuando los tama??os de gota se acercan al tama??o molecular.
| Δ P de las gotas de agua de diferentes radios en STP | ||||
|---|---|---|---|---|
| Radio de las gotitas | 1 mm | 0,1 mm | 1 micras | 10 nm |
| Δ P ( atm) | 0.0014 | 0.0144 | 1,436 | 143.6 |
Superficie del l??quido como un ordenador

Para encontrar la forma de la superficie m??nima delimitada por un cierto marco de forma arbitraria usando medios estrictamente matem??ticos puede ser una tarea desalentadora. Sin embargo, por la configuraci??n de la estructura de alambre y sumergi??ndolo en jab??n-soluci??n, una superficie de aproximadamente m??nima (exacta en ausencia de gravedad) aparecer?? en el jab??n-pel??cula resultante en cuesti??n de segundos. Sin un solo c??lculo, el jab??n de pel??cula llega a una soluci??n de una ecuaci??n de minimizaci??n complejo por s?? mismo.
La raz??n de esto es que la diferencia de presi??n a trav??s de una interfaz de fluido es proporcional a la curvatura media, como se ve en la Ley de Laplace. Para una pel??cula de jab??n abierta, la diferencia de presi??n es cero, por lo tanto la curvatura media es cero, y superficies m??nimas tienen la propiedad de curvatura media cero.
Los ??ngulos de contacto
Dado que el l??quido no puede existir en un vac??o perfecto, la superficie de cualquier l??quido es una interfaz entre el l??quido y que alg??n otro medio. La superficie superior de un estanque, por ejemplo, es una interfaz entre el agua del estanque y el aire. La tensi??n superficial, entonces, no es una propiedad del l??quido solo, sino una propiedad de la interfaz del l??quido con otro medio. Si es un l??quido en un recipiente, a continuaci??n, adem??s de la interfaz l??quido / aire en su superficie superior, hay tambi??n una interfaz entre el l??quido y las paredes del recipiente. La tensi??n superficial entre el l??quido y el aire es generalmente diferente (mayor que) su tensi??n superficial con las paredes de un recipiente. Y donde las dos superficies se encuentran, su geometr??a debe ser tal que todas las fuerzas de equilibrio.
 |
Cuando las dos superficies se encuentran, forman una ??ngulo de contacto,  , Que es el ??ngulo de la tangente a la superficie hace con la superficie s??lida. El diagrama de la derecha muestra dos ejemplos. El ejemplo de la izquierda es donde la tensi??n superficial l??quido-s??lido,
, Que es el ??ngulo de la tangente a la superficie hace con la superficie s??lida. El diagrama de la derecha muestra dos ejemplos. El ejemplo de la izquierda es donde la tensi??n superficial l??quido-s??lido, 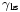 , Es menor que la tensi??n superficial l??quido-aire,
, Es menor que la tensi??n superficial l??quido-aire, 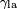 , Pero sin embargo es positivo, es decir
, Pero sin embargo es positivo, es decir
En el diagrama, tanto de las fuerzas verticales y horizontales deben cancelar exactamente en el punto de contacto. El componente horizontal de 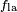 se cancela por la fuerza adhesiva,
se cancela por la fuerza adhesiva, 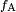 .
.
El equilibrio de las fuerzas m??s revelador, sin embargo, es en la direcci??n vertical. La componente vertical de 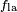 debe cancelar exactamente la fuerza,
debe cancelar exactamente la fuerza, 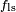 .
.
| L??quido | S??lido | El ??ngulo de contacto | |||
|---|---|---|---|---|---|
| agua |
| 0 ?? | |||
| etanol | |||||
| ??ter diet??lico | |||||
| tetracloruro de carbono | |||||
| glicerol | |||||
| ??cido ac??tico | |||||
| agua | parafina | 107 ?? | |||
| plata | 90 ?? | ||||
| yoduro de metilo | vidrio de sosa y cal | 29 ?? | |||
| vidrio de plomo | 30 ?? | ||||
| cuarzo fundido | 33 ?? | ||||
| mercurio | vidrio de sosa y cal | 140 ?? | |||
| Algunos ??ngulos de contacto l??quido-s??lido | |||||
Dado que las fuerzas est??n en proporci??n directa a sus respectivas tensiones superficiales, tambi??n tenemos:
donde
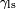 es la tensi??n superficial l??quido-s??lido,
es la tensi??n superficial l??quido-s??lido, 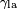 es la tensi??n superficial l??quido-aire,
es la tensi??n superficial l??quido-aire,  es el ??ngulo de contacto, donde un c??ncava menisco tiene ??ngulo de contacto de menos de 90 ?? y una convexa menisco tiene ??ngulo de contacto de m??s de 90 ??.
es el ??ngulo de contacto, donde un c??ncava menisco tiene ??ngulo de contacto de menos de 90 ?? y una convexa menisco tiene ??ngulo de contacto de m??s de 90 ??.
Esto significa que aunque la tensi??n superficial l??quido-s??lido, 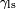 , Es dif??cil de medir directamente, se puede inferir a partir del ??ngulo de contacto medido f??cilmente,
, Es dif??cil de medir directamente, se puede inferir a partir del ??ngulo de contacto medido f??cilmente,  , Si la tensi??n superficial del l??quido-aire,
, Si la tensi??n superficial del l??quido-aire, 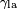 , Es sabido.
, Es sabido.
Esta misma relaci??n en el diagrama de la derecha. Pero en este caso se observa que debido a que el ??ngulo de contacto es menor que 90 ??, la tensi??n de l??quido / superficie s??lida debe ser negativo:
??ngulos de contacto especiales
Observe que en el caso especial de una interfaz de plata agua donde el ??ngulo de contacto es igual a 90 ??, la tensi??n superficial l??quido-s??lido es exactamente cero. Es dif??cil de limpiar el piso si l??quidos con contacto derrames ??ngulo ≈ 0 ??, como la gasolina, el queroseno, benceno, etc.
Otro caso especial es cuando el ??ngulo de contacto es exactamente 180 ??. Agua con especialmente preparado Teflon?? se acerca a esta. ??ngulo de contacto de 180 ?? se produce cuando la tensi??n superficial l??quido-s??lido es exactamente igual a la tensi??n superficial l??quido-aire.
M??todos de medici??n
Debido a la tensi??n superficial se manifiesta de diversos efectos, que ofrece una serie de rutas a su medida. Qu?? m??todo es ??ptima depende de la naturaleza del l??quido que se est?? midiendo, las condiciones en que su tensi??n se va a medir, y la estabilidad de su superficie cuando se deforma.
- M??todo del anillo Du No??y: El m??todo tradicional utilizado para medir la tensi??n superficial o interfacial. Propiedades de humectaci??n de la superficie o de la interfaz tienen poca influencia sobre esta t??cnica de medici??n. Fuerza m??xima de arrastre ejercida sobre el anillo por la superficie se mide.
- Una versi??n miniaturizada del m??todo de Du No??y utiliza una aguja de metal de peque??o di??metro en lugar de un anillo, en combinaci??n con una alta sensibilidad a la microbalanza de grabar m??xima de tracci??n. La ventaja de este m??todo es que los vol??menes de muestra muy peque??os (hasta de unas pocas decenas de microlitros) se pueden medir con una precisi??n muy alta, sin la necesidad de corregir para la flotabilidad (para una aguja o m??s bien, varilla, con una geometr??a apropiada). Adem??s, la medici??n se puede realizar muy r??pidamente, m??nimamente en unos 20 segundos. Primeros tensi??metros multicanal comerciales [CMCeeker] fueron construidas recientemente en base a este principio.
- Wilhelmy m??todo de la placa: Un m??todo universal especialmente adecuado para comprobar la tensi??n superficial en intervalos de tiempo largos. Una placa vertical del per??metro conocido est?? unido a un equilibrio, y se mide la fuerza debida a la humectaci??n.
- M??todo de la gota de Spinning: Esta t??cnica es ideal para medir tensiones interfaciales bajos. El di??metro de una gota dentro de una fase pesada se mide mientras tanto se hacen girar.
- M??todo de la gota colgante: tensi??n superficial e interfacial pueden ser medidos por esta t??cnica, incluso a temperaturas y presiones elevadas. Geometr??a de una gota se analiza ??pticamente. Para obtener m??s informaci??n, consulte Ca??da.

- M??todo de la burbuja de presi??n (m??todo de Jaeger): Una t??cnica de medici??n para determinar la tensi??n superficial en las edades de superficie cortos. Se mide la presi??n m??xima de cada burbuja.
- Gota m??todo de volumen: Un m??todo para determinar la tensi??n interfacial como una funci??n de la edad de interfaz. L??quido de una densidad se bombea a un segundo l??quido de una densidad diferente y el tiempo entre gotas producidas se mide.
- M??todo de ascensi??n capilar: El final de un capilar se sumerge en la soluci??n. La altura a la que la soluci??n alcanza el interior del capilar est?? relacionada con la tensi??n superficial por la ecuaci??n se discute a continuaci??n .
- Estalagm??metro: Un m??todo de ponderaci??n y la lectura de una gota de l??quido.
- M??todo de la gota s??sil: Un m??todo para determinar la tensi??n superficial y la densidad mediante la colocaci??n de una gota sobre un sustrato y la medici??n de la contactar ??ngulo (ver T??cnica de la gota s??sil).
Efectos
L??quido en un tubo vertical

Un viejo estilo de mercurio bar??metro consta de un tubo de vidrio vertical de aproximadamente 1 cm de di??metro parcialmente lleno de mercurio, y con un vac??o (llamado de vac??o de Torricelli) en el volumen sin llenar (v??ase el diagrama de la derecha). Observe que el nivel de mercurio en el centro del tubo es mayor que en los bordes, por lo que la superficie superior del mercurio en forma de c??pula. El centro de masa de la totalidad de la columna de mercurio ser??a ligeramente inferior si la superficie superior del mercurio fuera plana sobre toda la transversal de la del tubo. Pero la parte superior en forma de c??pula da ligeramente menos ??rea de superficie a toda la masa de mercurio. Una vez m??s los dos efectos se combinan para reducir al m??nimo la energ??a potencial total. Tal forma de la superficie se conoce como un convexa menisco.
La raz??n se considera el ??rea de la superficie de toda la masa de mercurio, incluyendo la parte de la superficie que est?? en contacto con el vidrio, es porque el mercurio no se adhiere al vidrio en absoluto. As?? que la tensi??n superficial del mercurio act??a sobre toda su ??rea de superficie, incluyendo donde est?? en contacto con el vidrio. Si en lugar de vidrio, el tubo se hace fuera de cobre, la situaci??n ser??a muy diferente. El mercurio se adhiere agresivamente al cobre. As??, en un tubo de cobre, el nivel de mercurio en el centro del tubo ser?? m??s bajo en lugar de m??s alto que en los bordes (es decir, ser??a un menisco c??ncavo). En una situaci??n en la que el l??quido se adhiere a las paredes de su recipiente, consideramos que la parte de la superficie del l??quido que est?? en contacto con el recipiente para que tenga una tensi??n superficial negativa. El fluido entonces trabaja para maximizar el ??rea de superficie de contacto. As?? pues, en este caso el aumento de la zona de contacto con los descensos de contenedores en lugar de aumenta la energ??a potencial. Esta disminuci??n es suficiente para compensar el aumento de la energ??a potencial asociada con la elevaci??n del fluido cerca de las paredes del recipiente.

Si un tubo es suficientemente estrecha y la adhesi??n de l??quido a sus paredes es lo suficientemente fuerte, la tensi??n superficial puede dibujar l??quido por el tubo en un fen??meno conocido como acci??n capilar. La altura de la columna se eleva a est?? dado por:
donde
 es la altura del l??quido se eleva,
es la altura del l??quido se eleva, 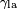 es la tensi??n superficial l??quido-aire,
es la tensi??n superficial l??quido-aire,  es la densidad del l??quido,
es la densidad del l??quido,  es el radio del capilar,
es el radio del capilar,  es la aceleraci??n debida a la gravedad,
es la aceleraci??n debida a la gravedad,  es el ??ngulo de contacto descrito anteriormente. Tenga en cuenta que si
es el ??ngulo de contacto descrito anteriormente. Tenga en cuenta que si  es mayor que 90 ??, como con mercurio en un recipiente de vidrio, el l??quido ser?? presionado en lugar de levantada.
es mayor que 90 ??, como con mercurio en un recipiente de vidrio, el l??quido ser?? presionado en lugar de levantada.
Charcos en una superficie

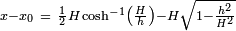 donde
donde 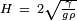

Verter el mercurio en una hoja plana horizontal de los resultados de vidrio en un charco que tiene un espesor perceptible (no intente esto con excepci??n de la campana extractora. El vapor de mercurio es un peligro t??xico). El charco se extender?? s??lo hasta el punto en que es un poco menos de la mitad de un cent??metro de espesor, y no m??s delgada. De nuevo, esto es debido a la acci??n de una fuerte tensi??n superficial del mercurio. La masa l??quida se aplana debido a que trae como gran parte del mercurio a un nivel tan bajo como sea posible. Pero la tensi??n superficial, al mismo tiempo, est?? actuando para reducir el ??rea total de la superficie. El resultado es el compromiso de un charco de un espesor casi fijo.
La misma demostraci??n tensi??n superficial se puede hacer con agua, pero s??lo sobre una superficie hecha de una sustancia que el agua no se adhiere a. La cera es una sustancia tal. El agua se vierte sobre una superficie lisa, plana y horizontal de cera, por ejemplo una l??mina encerada de cristal, se comportan de manera similar a la de mercurio verti?? sobre vidrio.
El espesor de un charco de l??quido sobre una superficie cuyo ??ngulo de contacto es 180 ?? viene dada por:
donde
- Click on the following link to visit or download this HTML page
 es la profundidad del charco en cent??metros o metros.
es la profundidad del charco en cent??metros o metros.  es la tensi??n superficial del l??quido en dinas por cent??metro o newtons por metro.
es la tensi??n superficial del l??quido en dinas por cent??metro o newtons por metro.  es la aceleraci??n debida a la gravedad y es igual a 980 cm / s 2 o 9,8 m / s 2
es la aceleraci??n debida a la gravedad y es igual a 980 cm / s 2 o 9,8 m / s 2  es la densidad del l??quido en gramos por cent??metro c??bico o kilogramos por metro c??bico
es la densidad del l??quido en gramos por cent??metro c??bico o kilogramos por metro c??bico

En realidad, los espesores de los charcos ser?? ligeramente menor que lo que se predice por la f??rmula anterior porque muy pocas superficies tienen un ??ngulo de contacto de 180 ?? con cualquier l??quido. Cuando el ??ngulo de contacto es menor que 180 ??, el espesor est?? dado por:
Para el mercurio en vidrio, 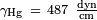 ,
, 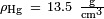 Y
Y 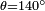 , Lo que da
, Lo que da 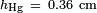 . Para el agua de parafina a 25 ?? C,
. Para el agua de parafina a 25 ?? C, 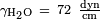 ,
, 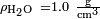 Y
Y 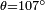 lo que da
lo que da 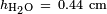 .
.
La f??rmula tambi??n predice que cuando el ??ngulo de contacto es de 0 ??, el l??quido se extiende en una capa micro-fina sobre la superficie. Tal superficie se dice que es totalmente humectable por el l??quido.
La ruptura de las corrientes en gotas

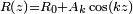 , Donde
, Donde 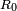 es el radio de la corriente no perturbada,
es el radio de la corriente no perturbada, 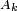 es la amplitud de la perturbaci??n,
es la amplitud de la perturbaci??n,  es la distancia a lo largo del eje de la corriente, y
es la distancia a lo largo del eje de la corriente, y  es el n??mero de onda
es el n??mero de onda En el d??a a d??a que todos observamos que un chorro de agua que sale de un grifo se romper?? en gotas, sin importar lo bien la corriente se emite desde el grifo. Esto es debido a un fen??meno llamado Inestabilidad Plateau-Rayleigh, que es enteramente una consecuencia de los efectos de la tensi??n superficial.
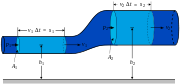
La explicaci??n de esta inestabilidad comienza con la existencia de peque??as perturbaciones en la corriente. Estos est??n siempre presentes, no importa c??mo suavizar la corriente es. Si las perturbaciones se resuelven en componentes sinusoidales, encontramos que algunos componentes crecen con el tiempo, mientras que otros se deterioran con el tiempo. Entre las que crecen con el tiempo, algunos crecen con mayor rapidez que otros. Si un componente se desintegra o crece, y lo r??pido que crece es totalmente una funci??n de su n??mero de onda (una medida de c??mo muchos picos y valles por cent??metro) y el radio de la corriente cil??ndrica inicial. El diagrama de la derecha muestra una exageraci??n de un solo componente.
Por supuesto de que existen todos los componentes posibles inicialmente en amplitudes aproximadamente iguales (pero min??sculas), el tama??o de las gotas final puede predecirse mediante la determinaci??n de qu?? componente por n??mero crece el m??s r??pido de onda. Como pasa el tiempo, es el componente cuya tasa de crecimiento es m??ximo que llegan a dominar y el tiempo ser?? el que aprieta el flujo en gotas.
Aunque un conocimiento profundo de c??mo sucede esto requiere un desarrollo matem??tico (ver referencias), el diagrama puede proporcionar una comprensi??n conceptual. Tenga en cuenta las dos bandas que se muestran que rodea la corriente de - uno en un pico y el otro en un canal de la ola. En la cubeta, el radio de la corriente es m??s peque??o, por lo tanto, de acuerdo con la Se incrementa ecuaci??n de Young-Laplace (discutido anteriormente) la presi??n debida a la tensi??n superficial. Del mismo modo en el pico de la radio de la corriente es mayor y, por el mismo razonamiento, se reduce la presi??n debido a la tensi??n superficial. Si este fuera el ??nico efecto, podr??amos esperar que la presi??n m??s alta en el canal ser??a exprimir l??quido en la zona de presi??n m??s baja en el pico. De esta forma vemos c??mo la ola crece en amplitud en el tiempo.
Pero el Ley de Laplace est?? influenciada por dos componentes de radio separadas. En este caso uno es el radio, ya se ha discutido, de la corriente en s?? mismo. El otro es el radio de curvatura de la propia ola. Los arcos armarios en el diagrama muestran ??stos en un pico y en un canal. Observe que el radio de curvatura en la artesa es, de hecho, negativo, lo que significa que, de acuerdo con Young-Laplace, en realidad disminuye la presi??n en el comedero. Asimismo el radio de curvatura en el pico es positivo y aumenta la presi??n en esa regi??n. El efecto de estos componentes est?? enfrente de los efectos de la radio de la corriente en s?? mismo.
Los dos efectos, en general, no se anulan exactamente. Uno de ellos tendr?? una magnitud mayor que el otro, en funci??n de n??mero de onda y el radio inicial de la corriente. Cuando el n??mero de onda es tal que el radio de curvatura de la onda domina la del radio de la corriente, tales componentes se desintegran con el tiempo. Cuando el efecto del radio de la corriente que domina de la curvatura de la ola, tales componentes crecen exponencialmente con el tiempo.
Cuando se hace todo el matem??ticas, se ha encontrado que los componentes inestables (es decir, componentes que crecen con el tiempo) son s??lo aquellos en los que el producto del n??mero de onda con el radio inicial es menor que la unidad ( 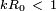 ). El componente que crece el m??s r??pido es el que tiene el n??mero de onda satisface la ecuaci??n:
). El componente que crece el m??s r??pido es el que tiene el n??mero de onda satisface la ecuaci??n:
Termodin??mica
Como se indic?? anteriormente, el trabajo mec??nico necesario para aumentar una superficie es 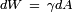 . Por lo tanto, a temperatura y presi??n constantes, la tensi??n superficial es igual a energ??a libre de Gibbs por ??rea de superficie:
. Por lo tanto, a temperatura y presi??n constantes, la tensi??n superficial es igual a energ??a libre de Gibbs por ??rea de superficie:
donde 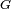 es energ??a libre de Gibbs y
es energ??a libre de Gibbs y 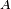 es el ??rea.
es el ??rea.
Termodin??mica requiere que todos los cambios espont??neos de estado est??n acompa??ados por una disminuci??n de energ??a libre de Gibbs.
De esto, es f??cil entender por qu?? la disminuci??n de la superficie de una masa de l??quido es siempre espont??nea ( 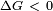 ), Siempre que no se acopla a cualquier otro cambio de energ??a. De ello se deduce que, para aumentar la superficie, hay que a??adir una cierta cantidad de energ??a.
), Siempre que no se acopla a cualquier otro cambio de energ??a. De ello se deduce que, para aumentar la superficie, hay que a??adir una cierta cantidad de energ??a.
Energ??a libre de Gibbs se define por la ecuaci??n, 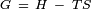 , Donde
, Donde 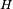 es la entalp??a y
es la entalp??a y  es la entrop??a . En base a esto y el hecho de que la tensi??n superficial es energ??a libre de Gibbs por unidad de ??rea, es posible obtener la siguiente expresi??n para la entrop??a por unidad de ??rea:
es la entrop??a . En base a esto y el hecho de que la tensi??n superficial es energ??a libre de Gibbs por unidad de ??rea, es posible obtener la siguiente expresi??n para la entrop??a por unidad de ??rea:
De Kelvin Ecuaci??n para superficies surge por la reordenaci??n de las ecuaciones anteriores. Se afirma que la entalp??a de superficie o energ??a superficial (diferente de la energ??a libre de superficie) depende tanto de la tensi??n superficial y su derivado con la temperatura a presi??n constante por la relaci??n.
Influencia de la temperatura

La tensi??n superficial depende de la temperatura. Por esa raz??n, cuando se da un valor para la tensi??n superficial de una interfaz, la temperatura debe indicarse expl??citamente. La tendencia general es que la tensi??n superficial disminuye con el aumento de la temperatura, alcanzando un valor de 0 en el temperatura cr??tica. Para m??s detalles ver Regla E??tv??s. Hay ecuaciones s??lo emp??ricos para relacionar la tensi??n superficial y la temperatura:
- E??tv??s:
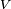 es el volumen molar de la sustancia
es el volumen molar de la sustancia 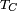 es el temperatura cr??tica
es el temperatura cr??tica  es una constante para cada sustancia.
es una constante para cada sustancia.
Por ejemplo para el agua k = 1,03 erg / ?? C (103 nj / K ), V = 18 ml / mol y T C = 374 ?? C.
Una variante de E??tv??s es descrito por Ramay y Shields:
donde el desfase de 6 grados Kelvin de temperatura proporciona la f??rmula con un mejor ajuste a la realidad a temperaturas m??s bajas.
- Guggenheim-Katayama:
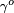 es una constante para cada l??quido y n es un factor emp??rico, cuyo valor es 11/9 para l??quidos org??nicos. Esta ecuaci??n tambi??n fue propuesto por van der Waals, que propuso, adem??s, que
es una constante para cada l??quido y n es un factor emp??rico, cuyo valor es 11/9 para l??quidos org??nicos. Esta ecuaci??n tambi??n fue propuesto por van der Waals, que propuso, adem??s, que 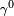 podr??a ser dado por la expresi??n,
podr??a ser dado por la expresi??n, 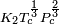 , Donde
, Donde 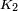 es una constante universal para todos los l??quidos, y
es una constante universal para todos los l??quidos, y 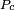 es el presi??n cr??tica del l??quido (aunque encontraron experimentos posteriores
es el presi??n cr??tica del l??quido (aunque encontraron experimentos posteriores 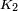 para variar a un cierto grado de un l??quido a otro).
para variar a un cierto grado de un l??quido a otro).
Tanto Guggenheim-Katayama y E??tv??s tienen en cuenta el hecho de que la tensi??n superficial llega a 0 a la temperatura cr??tica, mientras que Ramay y Shields falla para que coincida con la realidad en este punto final.
Influencia de la concentraci??n de soluto
Los solutos pueden tener diferentes efectos sobre la tensi??n superficial en funci??n de su estructura:
- No afecta, por ejemplo az??car
- Aumento de la tensi??n superficial, sales inorg??nicas
- Disminuir la tensi??n superficial progresivamente, alcoholes
- Disminuye la tensi??n superficial y, una vez que se alcanza un m??nimo, no m??s efecto: surfactantes
Lo que complica el efecto es que un soluto puede existir en una concentraci??n diferente en la superficie de un disolvente que en su mayor. Esta diferencia var??a de combinaci??n de un soluto / disolvente a otro.
Gibbs isoterma establece que: 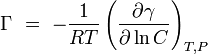
 que se conoce como concentraci??n superficial, que representa el exceso de soluto por unidad de ??rea de la superficie sobre lo que estar??a presente si la concentraci??n mayor prevaleci?? todo el camino a la superficie. Tiene unidades de mol / m 2
que se conoce como concentraci??n superficial, que representa el exceso de soluto por unidad de ??rea de la superficie sobre lo que estar??a presente si la concentraci??n mayor prevaleci?? todo el camino a la superficie. Tiene unidades de mol / m 2
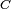 es la concentraci??n de la sustancia en la soluci??n a granel.
es la concentraci??n de la sustancia en la soluci??n a granel.
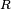 es el constante de los gases y
es el constante de los gases y 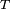 la temperatura
la temperatura
Ciertos supuestos se toman en su deducci??n, por lo tanto, Gibbs isoterma s??lo se puede aplicar a las soluciones ideales (muy diluidas) con dos componentes.
Influencia del tama??o de part??cula sobre la presi??n de vapor
La Relaci??n de Clausius-Clapeyron lleva a la otra ecuaci??n tambi??n atribuida a Kelvin. Esto explica por qu??, a causa de la tensi??n superficial, la presi??n de vapor para las peque??as gotas de l??quido en suspensi??n es mayor que la presi??n de vapor est??ndar de ese mismo l??quido cuando la interfaz es plana. Es decir que cuando un líquido se está formando pequeñas gotas, la concentración de equilibrio del vapor en su entorno es mayor. Esto surge debido a que la presión dentro de la gota es mayor que en el exterior.

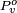 es la presión de vapor estándar para que el líquido a esa temperatura y presión.
es la presión de vapor estándar para que el líquido a esa temperatura y presión.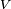 es el volumen molar.
es el volumen molar.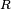 es el constante de los gases
es el constante de los gases
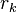 es el radio Kelvin, el radio de las gotitas.
es el radio Kelvin, el radio de las gotitas.
El efecto explica la sobresaturación de los vapores. En ausencia de sitios de nucleación, pequeñas gotas deben formar antes de que puedan convertirse en gotas más grandes. Esto requiere una presión de vapor muchas veces la presión de vapor en el punto de transición de fase.
Esta ecuación también se utiliza encatalizador dela química para evaluarmesoporosidad para sólidos.
El efecto puede ser visto en términos del número promedio de vecinos moleculares de moléculas de la superficie (ver diagrama).
La tabla muestra algunos valores calculados de este efecto de agua a diferentes tamaños de gota:
| P/P 0de las gotas de agua de diferentes radios en STP | ||||
|---|---|---|---|---|
| Radio de la gotita (nm) | 1000 | 100 | 10 | 1 |
| P/P 0 | 1,001 | 1,011 | 1,114 | 2.95 |
El efecto se vuelve claro para tamaños de gota muy pequeñas, como una gota de 1 nm radio tiene alrededor de 100 moléculas en el interior, que es una cantidad lo suficientemente pequeña como para requerir unamecánica cuánticaanálisis.
Tabla de datos
Los datos se tomaron deManual de Lange de Química, 10a ed.pp 1661-1665
| La tensión superficial de varios líquidos endinas / cm contra el aire Mezcla% 's son en peso | ||
|---|---|---|
| L??quido | Temperatura ?? C | La tensión superficial,?? |
| ??cido ac??tico | 20 | 27.6 |
| El ácido acético (40,1%) + Agua | 30 | 40.68 |
| Ácido acético (10,0%) + Agua | 30 | 54.56 |
| Acetona | 20 | 23.7 |
| ??ter diet??lico | 20 | 17.0 |
| Etanol | 20 | 22.27 |
| Etanol (40%) + Agua | 25 | 29.63 |
| El etanol (11,1%) + Agua | 25 | 46.03 |
| Glicerol | 20 | 63 |
| n-hexano | 20 | 18.4 |
| El ácido clorhídrico17,7M solución acuosa | 20 | 65.95 |
| Isopropanol | 20 | 21.7 |
| Mercurio | 15 | 487 |
| El metanol | 20 | 22.6 |
| noctano | 20 | 21.8 |
| El cloruro de sodio 6,0 Soluci??n acuosa M | 20 | 82.55 |
| La sacarosa (55%) + agua | 20 | 76.45 |
| Agua | 0 | 75.64 |
| Agua | 25 | 71.97 |
| Agua | 50 | 67.91 |
| Agua | 100 | 58.85 |